2. 中国气象局成都高原气象研究所,成都 610071
2. Institute of Plateau Meteorology, China Meteorological Administration, Chengdu 610071
评估气象站点代表性在站点保护、站点选址、气候变化研究等工作中都具有重要作用,但是定量化的评估却并不容易。基于遥感技术获取的相关数据或产品具有多尺度、范围广、周期性好等优点,可以在气象站点环境代表性评估方面发挥重要作用。王圆圆等(2011)利用了MODIS的地表温度(LST)产品,以基准气候站对其周围不同大小窗口内地表温度距平序列的解释方差作为度量,评估了我国142个基准气候站点的环境代表性,并将代表性与土地覆盖多样性和地形起伏度进行相关研究,这是一个很好的尝试。然而LST受地表因素影响大,空间变异性明显高于气温的空间变异性,用LST估算代表性会存在低估的风险,因此本文提出首先建立LST估算空气温度的模型;而后再用模型推算气温评估站点环境代表性的方法,这其中的关键则是建立准确的气温估算模型。文章详细回顾了LST估算气温的方法和研究进展,以藏东南林芝站点为例,介绍区域气温遥感估算模型建立方法,对模型加以验证,然后对比了基于LST和遥感估算气温计算的林芝站点代表性的结果。
1 LST估算近地面气温的方法近地面气温在气候、生态、灾害、公众健康等领域都至关重要。各种气候模式、估产模式、水文模式的迅速发展,对气温空间分布信息的需求日益强烈(Mostovoy et al,2006;Colombi et al,2007;De Wit et al,2008)。然而传统的基于气象站点所测气温在空间上不连续,由插值生成的气温分布图经常受到站点稀疏或布局不合理等因素的制约(Cristobal et al,2008;Vancutsem et al,2010)。为了获取连续的气温分布信息,采用遥感LST推算近地面气温的研究日益受到国内外学者的关注(Prihodko et al,1997;Florio et al,2004;Stathopoulou et al,2006;侯英雨等,2010;闵文彬等,2010;Shen et al,2011)。
LST具有空间上连续、分辨率高等特征,经过近30年的发展,LST的遥感反演已经趋于成熟,精度可达1 K以内(Wan et al,2004;Wang et al,2009)。虽然LST和地面气温紧密相关,但它们之间的关系非常复杂,两者之间的差异受地表能量平衡过程控制,而地表能量平衡与太阳辐射、大气、云、风速、土壤湿度和地表糙率等诸多因素有关,这些因素很难全部通过遥感光谱信息获取(Prince et al,1998)。因此,由LST推算空气温度主要依赖于建立经验关系,可以分为两种,一种是TVX(Temperature-Vegetation Index)方法,另一种是统计回归。TVX方法认为,空气温度近似等于全植被覆盖的冠层温度(Goward等,1994),对于一定大小且气象和水分条件均一稳定的区域,通过建立NDVI和LST的回归方程,即可外推全植被覆盖情况下的LST,即空气温度。TVX法具备一定的物理背景,但在实际应用中很容易受到限制。如TVX无法应用于非植被区或稀疏植被区,要求NDVI和LST具有负相关,全植被覆盖条件下NDVImax的取值受主观因素影响等(Stisen et al,2007;Karnieli et al,2011;Nieto et al,2011)。鉴于TVX方法的缺陷,一些学者利用统计方法直接建立空气温度和地表温度以及其他变量之间的回归模型。如Cresswell等(1999)利用太阳高度角的二阶多元回归模拟Meteosat地表温度和空气温度之间的差异,在南非地区的验证结果表明72%的样本的气温估算误差在3 K以内,r2达到了0.8。Jang等(2004)利用了更多的特征(包括AVHRR 5个波段的信息、高程、太阳高度角、日序),基于神经网络算法估算空气温度,结果表明,误差能控制在2 K以内。统计型的方法便于引入多种因素,在区域水平上的空气温度估算取得较好的效果。
由于MODIS/LST全球产品容易获取,且精度较高,近年来利用MODIS/LST数据推算区域气温的研究日益增加。MODIS搭载在极轨卫星上,每日过境时刻有变化,如果用LST估算过境瞬时气温,缺乏实际应用意义,因此学者们更热衷于利用MODIS/LST估算每日最高气温、最低气温或平均气温,如Shen等(2011)以中国北部地区和前苏联为研究区,利用每日晴空MODIS/LST产品,估算得到过境日最高气温和最低气温,平均绝对误差(Mean Absolute Error,MAE)为2.4~3.2 K;考虑到LST只有在晴空下才能获取,多天合成的LST更为常用,如Vancutsem等(2010)在非洲地区,利用8天合成的LST产品(MOD11A2),估算最低气温,平均绝对误差达1.73 K;Fu等(2011)分析了MOD11A2产品和青藏高原站点测量气温之间的关系,认为在生长季(5—10月)两者相关性较差,且地面气温测量高度也会影响相关性。
当前有很多研究都是利用多天合成LST估算最高气温、最低气温、或平均气温,多天合成的数据具备两个优势:(1) 缺值情况显著减少,(2) 时间尺度增加,气温估算精度容易提高。但是已有的研究中,往往忽略了合成期内晴空的数量(Vancutsem et al,2010;Fu et al,2011),而晴空数量在建立LST和气温的关系中是非常重要的,因为遥感LST合成产品只是提供了8天内晴空状态下LST的均值,如果8天内晴空越多,LST信息越丰富,对气温的估算也就会越准确,因此本研究将晴空日数信息引入气温估算模型中,这也是与以往研究最大不同之处。
在建立模型中,我们选择了LST、日序、合成时期内的晴空数量、太阳天顶角、高程等作为输入特征,采用了Cubist回归树算法(Lefsky, 2010; Quinlan, 1992)建立了空气温度估算模型,作为验证,将模型用于估算藏东南地区鲁朗站(由中国科学院青藏高原研究所设立)2008年气温,并与观测值进行对比。
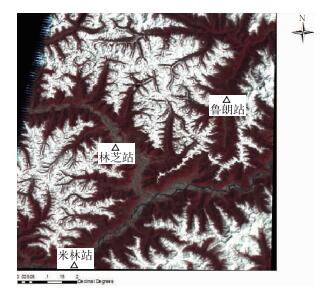
2 研究区、数据和方法介绍 2.1 研究区藏东南地区即青藏高原东南缘,是南亚气候系统与青藏高原相互作用的关键区,是青藏高原转运水汽的主要区域(高登义等,1985),该区地表特征也极为多样,天气气候复杂。然而受到气候恶劣、维持条件差等因素的影响,藏东南地区站点稀少,无法满足对该区域的全面认识,充分开发利用卫星资料是主要解决途径。研究区内有两个气象站点:林芝站(29.60°N、94.36°E)和米林站(29.21°N、94.21°E),另外还有一个由中国科学院青藏高原研究所设立的鲁朗站(29.77°N、94.74°E)(王永杰等,2010)。位置见图 1。
|
图 1 研究区TM图像以及站点位置 Fig. 1 TM image for study region and locations of the three stations |
采用上午星TERRA的LST产品(MOD11A2,collection 5) 为数据源,该数据是由每日晴空地表温度合成为8 d晴空LST平均值,空间分辨率1 km,时间跨度为2000—2011年,共12年的数据(其中2000年数据从DOY65开始,2011年数据到DOY145结束)。除LST,MOD11A2还提供合成天数,即由8天内的哪几天LST平均得到合成值,以及平均太阳天顶角等信息。根据气象站点经纬度信息,从遥感数据中提取LST时间序列、合成期晴天数量、太阳天顶角。由于LST一般在当地时10:30获取,因此本文将8 d平均日最高气温作为估算对象(如果是利用夜间获取的LST,则可以估算最低气温)。首先从气象数据共享网下载了林芝和米林站2000—2011年每日最高气温值,为了与LST产品相对应,处理成为8 d平均的日最高气温(后文均用符号T-air代表)。
2.3 分析方法首先分析了晴空天数、日序、太阳天顶角对LST和T-air之间相关性的影响。根据分析结果,选定合适的参数作为T-air估算模型的输入。在模型方面,选择了回归树模型算法(Cubist,由R语言实现,代码和使用说明见http://cran.r-project.org/web/packages/Cubist/index.html),该方法不断分裂节点,并针对节点上的所有样本建立线性拟合模型,模型的自变量是到达该节点前分裂时用到的属性,最后的估算主要利用叶节点的拟合模型,回归树模型将会简化成一系列的规则,形式如下,
当满足规则1时,采用回归模型1
当满足规则2时,采用回归模型2
当满足规则n时,采用回归模型n。
之所以采用回归树模型,是因为它有许多优点:(1) 可以自动生成多条规则,回归树算法过程相当于将样本空间分成多个子空间,每个子空间用一个线性模型去拟合(即一条规则),总体上构成非线性的模型;(2) 可以同时处理离散和连续数据,本研究中的晴空天数和日序属于离散型变量,而LST、太阳高度角、高程等属于连续型变量;(3) 可以不对数据作正态分布或其他分布类型的假设;(4) 可以评价输入特征的重要性,一个特征如果频繁地被用于分裂节点,则暗示该特征非常重要。
由Cubist回归树算法生成模型后,即可应用于区域尺度。考虑到藏东南地区海拔落差大,对气温有很大影响,但训练样本仅来自林芝和米林站(两站的海拔均约3000 m),无法将海拔高度作为自变量引入模型,因此本文按照高程每增加1 km气温下降6℃的规律对模型气温估算结果进行修正。
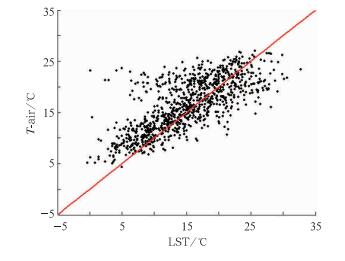
3 结果分析 3.1 LST和T-air的相关性通过合成处理后,林芝和米林站共有943个可用样本,图 2显示了LST和T-air的散点图,可以看出,两者具有较好的线性关系(相关系数为0.7172),但离散程度仍然较大,LST的变化范围在0~35℃,T-air的变化范围在5~25℃,LST的变化范围明显大于气温,同时从图中还可以看出有多个点的LST值明显低于T-air,这很可能是由于像元受到了云污染。
|
图 2 林芝和米林站LST和T-air散点图 Fig. 2 Scatter plot of daytime LST and 8-d averaged maximum air temperature (T-air) for Linzhi and Milin Meteorological Stations |
从表 1中可以看出,随着晴空天数的增加,LST和T-air的相关性逐渐增大,差值亦逐渐减小,在达到4 d以上,相关性稳定在0.8以上,差值稳定在3℃以内,因此晴空天数会对利用LST估算T-air造成影响。
|
|
表 1 LST和T-air之间的相关性和差值大小随晴空天数的变化趋势 Table 1 Variation trends of clear sky days on the correlation between daytime LST and near surface maximum air temperature (8-d averaged) |
将日序转化为季节,评价了季节对于LST和气温之间相关性和差异性的影响,从表 2中可以看出,夏季进入雨季,晴空少,有效数据少,LST和气温相关性小,差值也很大,其余三个季节,相关系数比较接近,但是LST和气温的差值在春、秋季更高,冬季更低,可能和冬季温度偏低有关。
|
|
表 2 LST与T-air差异的季节差异 Table 2 Seasonal differences of the difference between daytime LST and near surface maximum air temperature (8-d averaged) |
太阳天顶角反映了到达地表的能量值大小,由于卫星每日过境时间不固定,获取数据时的太阳天顶角也在发生变化,一般研究认为,当天顶角小且无云的时候,地表会吸收更多的能量,LST会比气温高出更多,但根据我们的数据计算,天顶角余弦和LST与T-air的差值之间不存在明显的正相关,相关系数只有0.0635,说明太阳天顶角的影响较小。这可能是由于太阳天顶角与气温日变化更相关。
3.5 模型结果分析根据前面分析结果,选择了LST、日序、晴空日数,作为自变量,建立T-air估算模型,回归树算法共生成了8条规则和相应的8个回归式(见附录),其中日序在所有分裂节点和建立模型的时候都会用到,说明对于T-air的估算很重要,这与Jang等(2004)的研究结论类似,一方面气温本身具有明显的季节变化,而本文估算T-air是8 d平均每日最高气温,季节影响因素得以进一步提高,分裂时所用日序的数值包括25,153,209,273,对应日期为1月25日、5月2日、6月28日、9月30日,在日序小于25或大于273时,分别只用一个模型即可估算T-air,说明冬季的模型比较简单,而当日序在25和273之间时,T-air和自变量之间的规律更加复杂,需要根据LST或晴空个数的情况,建立多个具有针对性的模型。LST和晴空日数也是非常重要的两个变量,它们在节点分裂时出现的比例分别是54%和34%,而且在所有回归模型中都被用到。从模型的形式来看,LST和晴空日数前的回归系数总为正,说明它们对气温的影响总是正向的;日序前的回归系数在日序小于209时为正,而在大于209时为负,和气温随季节的变化规律也是相符的。
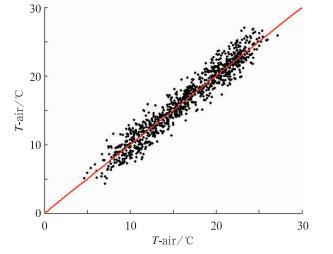
经过计算,模型的训练精度很高,决定系数为0.9328,均方根误差1.3129℃(见图 3)。为防止过学习,又试验了用70%的样本(随机选取)作为训练,剩下30%的样本作为检验样本,得出决定系数为0.9251,均方根误差1.4246℃,精度只是略为下降,说明模型不存在过学习。用T-air估算模型结合气温随高程的变化规律对鲁朗站2008年气温进行计算,结果显示,决定系数为0.9479,均方根误差1.4718℃,再次证明模型效果很好。从图 4中可以看出,大部分的估算值略高于观测值,这也是LST推算气温经常出现的问题(Stisen et al, 2007;Wloczyk et al,2011),可能与LST更能体现靠近地面的气温信息有关,而百叶箱测量高度一般是1.5 m,也可能和选用的气温随高程变化速度有关。
|
图 3 林芝和米林站T-air估算值与观测值的散点图(直线是1:1线) Fig. 3 Comparison between observed and estimated T-air values for Linzhi and Milin Meteorological Stations |

|
图 4 2008年鲁朗站气温估算与观测值对比 Fig. 4 Comparison between observed and estimated T-air values at the Lulang Station in 2008 |
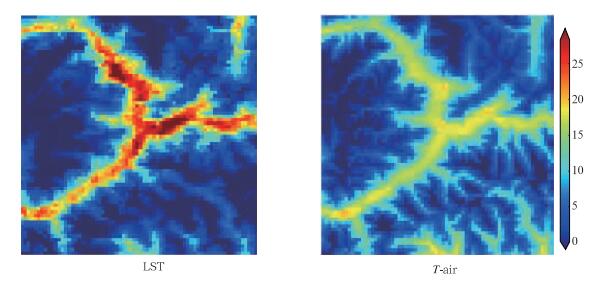
由Cubist回归树模型估算结果结合区域高程因素调节(利用1 km空间分辨率的DEM),即可计算全区2000—2011年的T-air,选定了70 km×70 km大小的区域(TM图像上表现区域,涵盖了林芝、米林、鲁朗三个站,由于回归模型仅基于两个站点计算得到,所以没有选择大区域),计算区域内每个像元的T-air,图 5即是一个示例图,从中可以看出,T-air的格局与LST接近,但是均一性更好,而且值域范围小。
|
图 5 2000年3月21—28日藏东南地区70 km×70 km由LST估算T-air示例 Fig. 5 An illustration of the LST map and the T-air map (70 km×70 km) estimated using the Cubist regression tree model on 21-28 March 2000 |
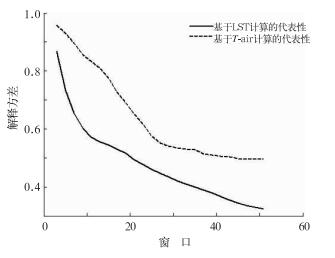
采用王圆圆等(2011)提出的方法,在林芝站点周围逐渐增大窗口,大小由3×3逐渐按步长2递增到51×51,计算站点所在像元对窗口LST或T-air时间序列距平的解释方差(即代表性),结果如图 6所示,随着窗口的增加,基于LST和T-air计算的代表性都有明显的下降,并都存在一个拐点,明显不同之处在于:(1) 基于LST计算的站点代表性明显偏小,随窗口增加,代表性下降速度很快。拐点出现较早,在拐点出现以后,解释方差仍然随着窗口的增大有较为明显下降,但是下降速度较拐点出现以前变小;(2) 基于T-air计算的代表性明显偏大,随窗口增加,代表性首先迅速下降,拐点出现较晚,到达拐点之后,代表性随窗口的增加变化较小,这说明拐点以前,站点代表性受空间距离的控制,但当达到一定距离以后,距离的作用减小,可能是因为林芝站点和窗口内像元同属一个大气候带,具备相似的气候特征,距离在代表性的计算中不再发挥重要作用,这和实际的情况是更加相符的。如果以解释方差超过0.75作为判断代表性的阈值(王圆圆等,2011),基于LST的代表窗口为3 km×3 km,明显偏低,而基于T-air计算林芝站可代表范围为15 km×15 km,更符合气温空间变异率偏低的实际情况。
|
图 6 林芝站对于不同窗口大小气温(或LST)时间序列距平的解释方差 Fig. 6 Explained variance of Linzhi Station for the air temperature (or LST) anomaly series at different window sizes |
气象站点代表性的定量评估在站点保护、站点新建等工作中都能发挥重要作用,基于遥感手段的代表性评估具有客观、多尺度等优势,但是中高空间分辨率的陆地卫星主要是观测地表状况,而气象站点的观测主要是针对近地面大气,两者之间的观测对象不完全一致,却又密切相关,为了能综合遥感和气象站点观测的优势,本文提出基于站点的遥感产品和气温观测信息建立模型,再由模型推算面上气温,最后由面上气温估算站点代表性,并在藏东南进行了尝试。文章基于藏东南林芝和米林气象站的近12年的气温资料以及MOD11A2产品信息,建立了研究区区域T-air(8天平均日最高气温)的估算模型,模型r2在0.92以上,均方根误差在1.5℃以内,高于以前的同类研究,合成天数、积日等都是估算模型的重要输入。利用该模型,可以得到区域T-air高分辨率分布图,用于对林芝站点代表性进行分析,结果表明,基于T-air计算得到的站点代表性更合理、更可信。
文章的关键是气温遥感估算模型的建立,进一步研究计划是尝试在更大的范围内建立模型,利用更多站点的信息,并考虑更多的影响因素,例如考虑云量、云高、云光学厚度等信息、卫星观测角度信息,此外,在进行区域气温计算时,当出现多天云覆盖而没有LST的情况,则无法进行气温估算,我们希望能够开发一种兼顾气温的时间和空间变化规律的插值技术,实现气温遥感的无缝制图。
附录
藏东南林芝地区基于遥感数据估算T-air的模型
Rule 1: [82 cases]
IF DOY < =25 THEN
T-air=2.71114+0.314*LST+0.84*clear-skys+0.0099*DOY
Rule 2: [241 cases]
IF DOY > 273 THEN
T-air = 36.28592 -0.0822*DOY + 0.211*LST + 0.21* clear-skys
Rule 3: [40 cases]
IF LST < = 9.100 & DOY > 25 & DOY < = 209 THEN
T-air = 2.4556 + 0.0909*DOY + 0.385*LST + 0.11*clear-skys
Rule 4: [47 cases]
IF LST > 9.100 & clear-skys > 5 & DOY < = 209 THEN
T-air = -1.87282 + 0.0506*DOY + 1.36*clear-skys + 0.346*LST
Rule 5: [286 cases]
IF LST > 9.100 & clear-skys < = 5 & DOY < = 153 THEN
T-air = 2.42984 + 0.0859*DOY + 0.188*LST + 0.59*clear-skys
Rule 6: [86 cases]
IF LST < = 18.2600 & DOY > 209 & DOY < = 273 THEN
T-air = 36.55526 -0.0712*DOY + 0.41*clear-skys + 0.061 LST
Rule 7: [72 cases]
IF LST > 18.2600 & DOY > 209 THEN
T-air = 31.08562 -0.0697*DOY + 0.306*LST + 0.49*clear-skys
Rule 8: [127 cases]
IF DOY > 153 & DOY < = 209 THEN
T-air = 13.44672 + 0.0242 DOY + 0.65*clear-skys + 0.153*LST
高登义, 邹捍, 王维, 1985. 雅鲁藏布江水汽通道对降水的影响[J]. 山地学报, 3(4): 239-249. |
侯英雨, 张佳华, 延昊, 等, 2010. 利用卫星遥感资料估算区域尺度空气温度[J]. 气象, 36(4): 75-79. DOI:10.7519/j.issn.1000-0526.2010.04.013 |
闵文彬, 李跃清, 2010. 反演四川盆地地表温度与地面同步气温、地温观测之的相关性试验[J]. 气象, 36(6): 101-104. DOI:10.7519/j.issn.1000-0526.2010.06.016 |
王永杰, 马耀明, 朱志鹍, 等, 2010. 藏东南地区鲁郎河谷近地层气象要素变化特征[J]. 高原气象, 29(1): 63-69. |
王圆圆, 李贵才, 张艳, 2011. 利用MODIS/LST产品分析基准气候站环境代表性[J]. 应用气象学报, 22(2): 214-220. DOI:10.11898/1001-7313.20110210 |
Colombi A, De Michele C, Pepe M, et al, 2007. Estimation of daily mean air temperature from MODIS LST in Alpine areas[J]. EARSeleProceeding, 6(1): 38-46. |
Cresswell M P, Morse A P, Thomoson M C, et al, 1999. Estimating surface air temperatures from Meteosat land surface temperatures using an empirical solar zenith angle model[J]. Int J Remote Sen, 20(6): 1125-1132. DOI:10.1080/014311699212885 |
Cristobal J, Ninyeroloa M, Pons X, 2008. Modeling air temperature through a combination of remote sensing and GIS data[J]. J Geophy Res, 113: D13106. DOI:10.1029/2007JD009318 |
De Wit A J W, Van Diepen C A, 2008. Crop growth modeling and crop yield forecasting using satellite-derived meteorological inputs[J]. Int J Appl Earth Obs Geoinfor, 10(4): 414-425. DOI:10.1016/j.jag.2007.10.004 |
Florio E N, Lele S R, Chang Y C, et al, 2004. Integrating AVHRR satellite data and NOAA ground observations to predict surface air temperature: A statistical approach[J]. Int J Remote Sen, 25(15): 2797-2994. |
Fu G, Shen Z X, Zhang X Z, et al, 2011. Estimating air temperature of an alpine meadow on the northern Tibetan Plateau using MODIS land surface temperature[J]. Acta Ecologic Sinica, 31: 8-13. DOI:10.1016/j.chnaes.2010.11.002 |
Goward S N, Waring R H, Dye D G, et al, 1994. Ecological remote-sensing at OTTER-Satellite macroscale observations[J]. Ecological Applications, 4: 322-343. DOI:10.2307/1941937 |
Jang J D, Viau A A, 2004. Neural network estimation of air temperature from AVHRR data[J]. Int J remote sens, 25(21): 4541-4554. DOI:10.1080/01431160310001657533 |
Karnieli A, Agam N, Pinker R T, et al, 2011. Use of NDVI and land surface temperature for drought Assessment: Merits and limitations[J]. Ame Meteoro Soc, 23(3): 618-633. |
Lefsky M A, 2010. A global forest canopy height map from the Moderate Resolution Imaging Spectroradiometer and the Geoscience Laser Altimeter System[J]. Geophy Res Lett: 37. DOI:10.1029/2010GL043622 |
Mostovoy G V, King R L, Reddy K R, et al, 2006. Statistical estimation of daily maximum and minimum air temperature from MODIS LST data over the state of Mississippi[J]. GIScience Remote Sens, 43(1): 78-110. DOI:10.2747/1548-1603.43.1.78 |
Nieto H, Sandhold I, Aguado I, et al, 2011. Air temperature estimation with MSF-SEVIRI data: Calibration and validation of the TVX algorithm for the Iberian Peninsula[J]. Remote Sens Enviro, 115: 107-116. DOI:10.1016/j.rse.2010.08.010 |
Prihodko L, Goward S N, 1997. Estimation of air temperature from remotely sensed surface observations[J]. Remote Sens Enviro, 60(3): 335-346. DOI:10.1016/S0034-4257(96)00216-7 |
Prince S D, Goetz S J, Dubayah R O, et al, 1998. Inference of surface and air temperature, atmospheric precipitable water and vapor pressure deficit using Advance Very High-Resolution Radiometer satellite observations: Comparison with field observations[J]. J Hydrology, 212-213: 230-249. DOI:10.1016/S0022-1694(98)00210-8 |
Quinlan J R, 1992. Learning with continuous classes[J]. Proceedings of the 5th Australian Joint Conference on Artificial Intelligence: 343-348. |
Shen S H, Leptoukh G G, 2011. Estimation of surface air temperature over central and eastern Eurasia from MODIS land surface temperature[J]. Enviro Res Letts. DOI:10.1088/1748-9326/6/4/045206 |
Stathopoulou M, Cartalis C, Chrysoulakis N, 2006. Using midday surface temperature to estimate cooling degree-days from NOAA-AVHRR thermal infrared data: An application for Athens, Greece[J]. Solar Energy, 80: 414-422. DOI:10.1016/j.solener.2005.02.004 |
Stisen S, Sandholt I, Norgaard A, et al, 2007. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa[J]. Remote Sens Enviro, 110(2): 262-274. DOI:10.1016/j.rse.2007.02.025 |
Vancutsem C, Ceccato P, Dinku T, et al, 2010. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystem over Africa[J]. Remote Sens Enviro, 114: 449-465. DOI:10.1016/j.rse.2009.10.002 |
Wan Z, Zhang Y, Zhang Q, et al, 2004. Quality assessment and validation of the MODIS global land surface temperature[J]. Int J Remote Sens, 25: 261-274. DOI:10.1080/0143116031000116417 |
Wang K C, Liang S L, 2009. Evaluation of ASTER and MODIS land surface temperature and emissivity products using long-term surface longwave radiation observations at SURFARD sites[J]. Remote Sens of Enviro, 113: 1556-1565. DOI:10.1016/j.rse.2009.03.009 |
Wloczyk C, Borg E, Richter R, et al, 2011. Estimation of instantaneous air temperature above vegetation and soil surface from Landsat 7 ETM+ data in northern Germany[J]. Int J Remote Sens, 32(24): 9119-9136. DOI:10.1080/01431161.2010.550332 |
 2014, Vol. 40
2014, Vol. 40 