引言

我国CINRAD/SA新一代天气雷达采用的是美国WSR-88D天气雷达的观测模式，最低观测仰角为0.5°(李柏等，2013)，该观测模式适合于平原地区的雷达，而我国地形比较复杂，山区较多、丘陵地区大，不少新一代天气雷达架设在高山顶上，当高山顶上雷达采用最低仰角为0.5°模式观测时，在距离雷达200 km处，波束中心海拔高度已经超过了4 km，低层降水回波的探测能力远远不足，进而导致雷达定量估测降水值偏低。

针对高山雷达低空探测能力不足的问题，有不少学者提出了负仰角观测模式。美国强风暴实验室Brown等(2002)和Vincent等(2003)根据现在使用的WSR-88D天气雷达体扫模式，对位于蒙大纳州、密苏拉市附近一座高山上的KMSL多普勒雷达通过负仰角模拟不同天气的探测效果，对比+0.5°与-0.8°仰角的探测情况，结果表明：当采用最低+0.5°仰角扫描时，在雷达附近估测雨强约为80%，距雷达220 km外仅有1%；但当采用最低-0.8°仰角扫描时，远距离220 km外估测雨强仍可达80%~95%。负仰角扫描能明显提高低对流层天气系统的探测能力，如辐合/辐散场、下击暴流、阵风锋等，提高定量估测降水准确率和台风、暴雨等灾害性天气的远距离监测、预警能力(刘晓阳等，2010；王德胜等，2012；钟敏等，2012；张亚萍等，2013；庄薇等，2013)。张沛源等(2009)指出为了对近地面层进行探测，进行零度或负仰角扫描是必要的，但由于地球曲率的影响，需要考虑遮挡问题。徐八林等(2008)研究认为：负仰角扫描能明显提高雷达远距离回波探测效果，可弥补常规业务扫描模式下高山雷达探测低层回波能力不足的问题，对文山雷达一次冰雹过程探测分析，认为负仰角扫描对强对流天气能获得较好的低层探测效果。

关于地物回波的识别，各种研究成果均表明模糊逻辑法具有较好的识别效果。目前逐步将该方法推向实际业务中。该方法原理是从雷达资料中提取用于区分不同雷达回波(如降水、地物)的物理量，然后根据降水、地物回波的特征设置隶属函数，对这些物理量模糊化处理，得到所有物理量对于不同类型回波的0~1取值范围的判据，对这些判据进行加权累加，当某点地物回波的判据超过事先给定的阈值时，该点就被识别为地物回波。刘黎平等(2007)在这方面做了大量的工作，开展用新一代天气雷达体扫资料基于模糊逻辑的分布式超折射地物回波识别，江源等(2009)运用CSI(critical success index)评判标准确定了模糊逻辑超折射地物回波识别的最佳线性梯形隶属函数，通过识别效果分析表明改进后的方法可以更好地识别地物/超折射回波，减少对降水回波的误判。

2011年，经过中国气象局批准，福建省气象局组织长乐新一代天气雷达开展负仰角观测模式试验，结果证明了上述问题，负仰角扫描模式的确提高了中尺度对流性天气系统的探测能力，有利于监测台湾海峡的台风天气过程(张扬成，2012)。但是长期的业务运行发现，负仰角扫描模式同时又带来了一些问题，诸如在特定大气条件下台湾岛反射回来的超折射回波，该超折射回波轮廓与台湾地形非常一致，大量统计结果表明该超折射回波强度值高，垂直梯度小，采用模糊逻辑法不能较好地识别。因此需要根据回波特征设计新的方法给予解决，基于此，本文借助模式识别理论提出一种新的方法，即模板匹配法，根据该超折射回波与台湾地形相一致的特征，设计模板对负仰角扫描模式下带来超折射回波给予滤除，以至于不会对负仰角在业务上的使用造成实质性影响。

1 长乐雷达负仰角观测模式

长乐雷达继续保留使用VCP11、VCP21两种降水观测模式，同时增加VCP12和VCP22(分别由VCP11和VCP21改进而得)两种降水模式，调整后的降水观测模式增加到4种。VCP12模式共18个仰角，VCP22模式共9个仰角(表 1)。对VCP12模式，低层5个仰角即-0.5°、0°、0.49°、0.99°、1.48°采用分离取样方式CS/CD，中间的7个仰角即1.97°、2.48°、3.05°、3.70°、4.46°、5.35°、6.41°采用交替扫描方式B，高层的6个仰角即7.63°、9.08°、10.79°、12.75°、15.21°、18.34°采用不考虑距离折叠的连续多普勒方式CDX；对VCP22模式，低层4个仰角即-0.3°、0°、0.49°、1.45°采用分离取样方式CS/CD，中间的3个仰角即2.40°、3.35°、4.30°采用交替扫描方式B，高层的2个仰角即6.0°、9.9°采用不考虑距离折叠的连续多普勒方式CDX。

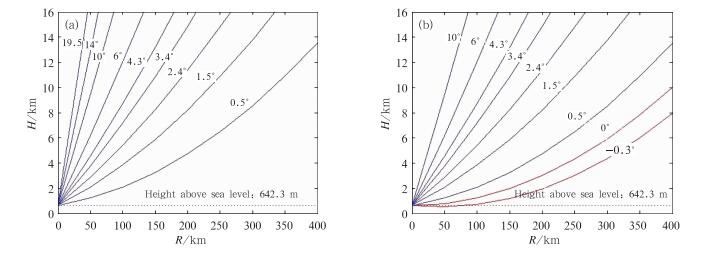
图 1为长乐雷达在VCP21和VCP22模式下雷达电磁波射线传播路径的模拟仿真，从图中可以看出：在VCP21模式下，200 km以外低空探测能力受到很大的限制，但当采用VCP22模式时，0°和-0.3°仰角扫描弥补了远距离处低层降水回波的探测，有助于提高中尺度天气系统的监测能力，特别是当沿海台风进入雷达探测范围时，采用VCP22模式更有利于监测和预警信息的提前发布。

2 雷达电磁波传播特征

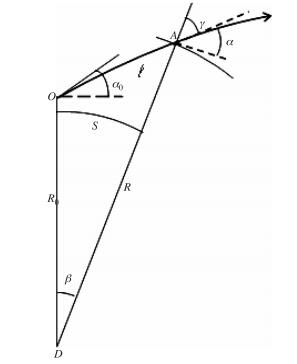
如图 2所示，A点处的曲率k计算公式：

$ k = - \frac{{\cos \alpha }}{n}\frac{{{\rm{d}}n}}{{{\rm{d}}z}} $

(1)

式中，α为波束与地面的夹角，n为大气折射指数。从中可以看出，如果大气为均有介质，dn/dz=0，不管仰角如何变化，雷达射线都是直线；当雷达垂直发射时(即α=90°)，不管折射指数如何变化，k=0，雷达射线总保持为垂直向上直线传播；除这两种情况之外，雷达射线的曲率均不为零，射线都会发生弯曲，曲率大小与射线的仰角和折射指数梯度的大小有关。

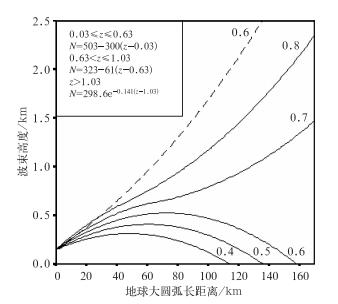
图 3给出了雷达射线传播路径示意图，分为三种情况：(1) 如果实际大气折射处于零折射和临界折射之间，dn/dz>-1/R_e，仰角将随探测距离的增加而变大，高度随传播距离的增加而变高；(2) 如果实际大气折射为临界折射状态，dn/dz=-1/R_e，仰角始终不变，α₀>0时，高度随探测距离的增加而变高；α₀=0时雷达射线与地表平行，高度不变；(3) 如果实际大气中出现超折射，dn/dz < -1/R_e，仰角将随探测距离增加而变小，并在等于零之后继续下降至负值。在仰角变为零之前，射线高度随探测距离的增加而变高，仰角变为负值后，射线高度随探测距离的增加而变低。dn/dz绝对值越大，曲率k越大，超折射越严重，雷达射线触及地表，导致异常传播(俞小鼎等，2006；张培昌等，2005)。

大气折射指数与气压、温度、湿度的变化关系式如式(2) 所示，大气折射指数随高度的变化公式如式(3) 所示：

$ \begin{array}{l} n = \left[ {\frac{{77.6}}{T}{P_d} + \frac{{77.6}}{T}\left({1 + \frac{{4810}}{T}} \right)e} \right] \times {10^{ - 6}} + 1\\ \;\;\;\;\;N = \left({n - 1} \right) \times {10^{ - 6}} \end{array} $

(2)

$ \frac{{{\rm{d}}N}}{{{\rm{d}}Z}} = \frac{{\partial N}}{{\partial T}}\frac{{{\rm{d}}T}}{{{\rm{d}}Z}} + \frac{{\partial N}}{{\partial {p_d}}}\frac{{{\rm{d}}{p_d}}}{{{\rm{d}}Z}} + \frac{{\partial N}}{{\partial e}}\frac{{{\rm{d}}e}}{{{\rm{d}}Z}} $

(3)

从式(3) 推导可得，当大气处于逆温或逆湿状态时(dT/dZ>0，de/dZ>0)，由于∂N/∂T < 0和∂N/∂e < 0，则dN/dZ为负值且绝对值较大，容易出现超折射现象。

逆温越明显，dN/dZ为越小(dN/dZ为负值，绝对值越大)，曲率k越大，超折射越严重；高层湿度增加但没有形成降水，对射线影响不如温度明显。

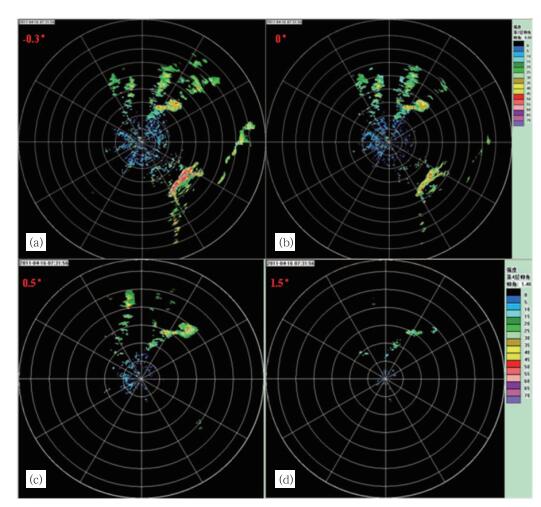
3 长乐雷达强超折射回波特征

图 4为2011年4月16日北京时07:31:56长乐雷达采用VCP22体扫模式下4个低仰角反射率因子回波图，由图可知，在雷达东北方向100~300km范围内，探测到对流性降水回波，与0.5°和1.5°的仰角探测对比，-0.3°和0°仰角所探测到降水回波的范围明显增大，强度明显增强，表明VCP22模式提高了中远距离回波的探测能力。

对比图 1长乐雷达VCP22模式下射线传播路径与图 3超折射条件下雷达低仰角射线传播路径示意图，若大气处于逆温或逆湿状态下，电磁波射线容易弯向地面传播造成超折射，由于长乐雷达采用负仰角扫描，则电磁波射线更容易弯向地面传播，形成的超折射更为严重。如图 4所示，在距雷达东南方向150~300 km处为超折射回波，是由台湾岛地形反射而形成的，其形状轮廓与台湾岛地形非常一致，在-0.3°、0°，有时也会在0.5°仰角出现。

目前，业务上使用模糊逻辑法识别超折射回波，模糊逻辑法是指运用统计方法分析各种雷达回波特征，找出地物回波不同于降水回波的特点，对这些特征给以相同的权重，得到一个表明每个距离库中受地物回波影响可能性的量化数值，最终识别出那些超过某一阈值的地物回波信息。Kessinger等(2003)，江源等(2009)，刘黎平等(2007)方法中使用的反映地物和降水回波差异的7个物理量，包括从回波强度中提取的4个特征量:反射率水平纹理(TDBZ)、反射率垂直梯度(GDBZ)、沿径向方向的变号(SIGN)、沿径向的库间变化程度(SPIN)；从径向速度和速度谱宽中提取的3个特征量:径向速度的区域平均值(MDVE)、方差(SDVE)、速度谱宽的区域平均值(MDSW)。

经过统计可知，长乐雷达的超折射回波在回波水平纹理、回波库间变化程度、径向速度及谱宽等特征量与“一般超折射回波”的变化几乎一致。不同的是“一般超折射回波”多数都只出现在最低仰角0.5°层上，在1.5°仰角层以上几乎不会出现，而长乐雷达的超折射回波是在负仰角扫描模式下造成的，在低两层仰角-0.3°和0°仰角层上都特别明显，有时候也会在第三层0.5°仰角上出现，其回波强度值高，垂直梯度小。为了区分它与一般超折射回波，称之为高山雷达的“强超折射回波”。

模糊逻辑法中反射率垂直梯度特征量定义为GDBZ=w(R)(Z_up-Z_low)，w(R)=1时，GDBZ=(Z_up-Z_low)。w(R)=1/(H_up-H_low)时，为Zhang等(2004)和Steiner等(2002)提出的给定距离库在当前仰角和上层仰角的反射率因子差与对应高度差的比值计算垂直变化VDBZ=(Z_up-Z_low)/(H_UP-H_LOW)，江源等(2009)分析了降水回波和地物回波的特征差异，参加分析的真实地物回波点有43251个，对流性降水回波点有11119个，层状云降水有107558个，对所有真实回波点计算的特征量进行统计分析，结果表明，权值w(R)=1时，GDBZ < -20为地物或超折射回波的概率很大；当w(R)=1/(H_up-H_low)时，VDBZ < -15为地物或超折射回波的概率很大。统计图 4所示的长乐雷达强超折射回波在130°~140°径向、200~210 km范围内的反射率垂直梯度GDBZ、VDBZ，结果如表 2和表 3所示，在参与统计的100个强超折射回波点中，有67个回波点的GDBZ>-20，有50个回波点的VDBZ>-15，不符合地物、超折射回波特征统计结论，因此模糊逻辑法不适合滤除长乐雷达的强超折射回波。

4 长乐雷达强超折射回波识别 4.1 模板匹配法原理

由于长乐雷达负仰角观测模式下的强超折射回波是由台湾岛反射回来的，其回波形状轮廓与台湾岛地形极其相似，因此可结合地形特征设计长乐雷达的强超折射特征模板，与实际回波图相匹配，当相似匹配度达到一定的比例，则认为是强超折射回波，予以剔除。

模板匹配法为模式识别上的一种算法，多用在计算机图像处理和特征识别等学科(谷秋頔等，2011；李忠海等，2011)，本文首次将该理论用于超折射回波特征识别上，滤除长乐雷达负仰角扫描造成的强超折射回波。其实质是以标准数据为模板，以模板特点为依据实现强超折射特征匹配，标准数据做成的模板与实际回波识别所用到的模板尺寸相一致。模板匹配需要参数衡量，主要有：(1) 求重合度和差别函数；(2) 求相似度；(3) 相关度量标准；(4) 相似度指标等。

4.2 特征模板识别

具体识别步骤为：

(1) 建立模板，由于该超折射回波是固定发生在台湾岛所在的区域，因此需要对该区域内强超折射回波的分布情况进行统计，该区域内的强超折射回波分布在范围(方位110°~165°，距离库185~400) 内，通过选取20个长乐雷达的强超折射回波个例样本，观测时间在2011年4月7—16日之间，其中每两个数据的观测时间间隔大于1 h，对该区域内的反射率因子数据做统计，求20个样本在强超折射回波区域内每个点的均值，将均值做成标准数据模板存储在计算机中；

(2) 将待识别的回波数据与模板数据相匹配，特征模板匹配的数学描述(付先平等，2011；严萍等，2011)：

$ D = \frac{1}{n}\sum\limits_{k = 1}^n {A\left(k \right)} \times {\left[ {I\left(k \right) - T\left(k \right)} \right]^2}, $

式中，A(k)为第k个特征的权值，本文中权值都取1，I(k)为待匹配数据的第k个特征，T(k)为模板数据中第k个特征，D为匹配值，表示匹配的特征与模板数据特征的差异程度，匹配值越小，两个回波特征越一致；

(3) 统计降水回波、强超折射回波数据与模板数据的匹配值，根据两类回波匹配值的差异制定相似度指标，达到最优匹配。

4.3 识别结果分析

由于在强超折射发生时，发生降水的可能性非常小，目前在个例分析中尚未遇到过在模板区同时存在降水和地物这种情况。本文分两种情况对地物进行识别，(1) 在模板区只有地物回波；(2) 在模板区只有降水回波。

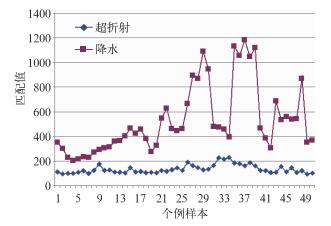
选取了长乐雷达50个地物回波样本和50个降水回波样本，降水回波样本是指在模板区只有降水回波，将这些样本数据与模板相匹配，计算匹配值，结果如图 5所示，匹配值越小，则相似度越高，在模板区发生强超折射的可能性越大，本文将匹配值D=200设为相似度指标(阈值)，即待识别的回波数据经过与模板匹配后，当匹配值D < 200时，则认为是强超折射回波，给予剔除。另外抽取50个地物回波样本和50个降水回波样本，统计当匹配值D < 200时地物回波识别率和降水回波误判率，结果如表 4所示，地物回波识别准确率在90%以上，降水回波误判为地物回波的概率为0%，充分表明采用模板匹配法可以有效识别长乐雷达在特定大气条件下的强超折射回波，且当模板区域只有降水回波时不会被误判为地物回波。

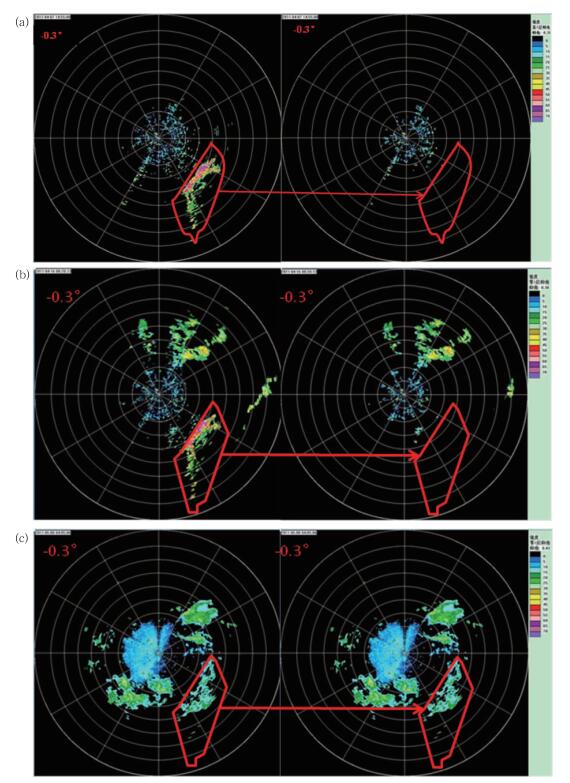
图 6为模板匹配法对长乐雷达在模板区只有地物和模板区只有降水时的识别结果。

5 结论和讨论

受地球曲率影响，高山雷达在现有的VCP11/21模式下探测盲区较大，对低层降水回波的探测能力严重不足，在引进负仰角扫描模式VCP12/22后，有效提高了对低层降水回波的观测能力，尤其是在对台风等灾害性天气的远距离监测和预警中显得尤为重要。

但是负仰角扫描也带来了负面效应，如长乐雷达的强超折射回波，本文分析了该强超折射回波的特征，得出以下结论：

(1) 长乐雷达的强超折射回波不符合一般地物、超折射回波的特征统计结论，因此不宜采用模糊逻辑法滤除。

(2) 由于该强超折射回波形状轮廓与台湾岛地形极其相似，提出采用模板匹配法识别，选择合适的模板，将待识别的回波数据与模板数据相匹配，计算匹配值，匹配值越小，则相似度越高，发生强超折射的概率越高。

(3) 抽取长乐地物和降水回波样本，针对本文所用的模板做统计，当匹配值D < 200时，地物回波识别准确率在90%以上，且当模板区只有降水回波时，不会被误判为地物回波。

长乐雷达在采用负仰角模式下提高了对低层降水回波的观测能力，模板匹配法既不影响对低层降水回波的探测，而且能解决其带来的强超折射回波负面效应，目前该方法正在试运行，即将应用到中国新一代天气雷达建设业务软件系统开发ROSE项目中。