引言

水是生命之源，是支撑社会经济系统发展不可替代的资源。由于全球变化、人类活动的负面影响，许多地区正在发生严重的水危机。水问题已成为制约国家和区域可持续发展的关键因子之一。因而水文科学研究也成为国际地球科学发展中的一个重要方面。面雨量是一个地区的降水量总和，能够客观地描述该区域实际降水概况。面雨量的多少对一个区域的河水径流量影响很大，是水分循环、气候-水文模式研究中一个重要的基础数据，也是洪水预报中非常重要的指标之一，它是气象与水文相互结合的桥梁和纽带。

目前国内外针对面雨量的研究方法主要有实测值插值法、遥感相关法和统计模型法等。实测值插值法是通过已知点的实测数据来推求未知点的数据，主要方法有：算术平均法、等雨量线法及泰森多边形法等。算术平均法简便易行，但仅适用于流域面积小、地形起伏不大，且测站多而分布又较为均匀的流域；格点法能较好地反映降水的连续性；等雨量线法精度高，但较多地依赖于分析技能，而且操作比较复杂，不便于日常业务使用；泰森多边形法或三角形法，考虑了各雨量站的权重，而且当测站固定不变时，各测站的权重也不变，比算术平均法更合理，精度也较高，因此应用较广(徐晶等，2001；2005)。但是这些方法没有考虑流域内各地的气候差异和地形作用所引起的降水分布不均匀对面雨量的影响。遥感相关法是指利用卫星、雷达等探测资料对降水进行估算的一种方法。卫星、雷达资料具有时间连续性、高空间分辨率以及范围覆盖面广等特点，这些能够弥补地面观测站的不足，但是由于仪器本身的误差，估算的降水还需由实测资料校正才能与实测值相符(Wood et al，2000；Seo et al，1990；何健等，2006；丛芳等, 2011)。在卫星产品的使用方面：王登炎等(2003)利用变分法结合卫星估算降水和数值预报产品进行面雨量预报；潘永地等(2005)利用气象卫星水汽通道资料修正地面观测资料的插值结果，再计算流域面雨量。邱冰等(2010)利用MODIS数据中的云、大气参数因子、结合实测数据，利用BP神经网络方法在博斯腾湖流域山区和盆地建立降水估算模型，所建模型在山区日降水量的效率系数达到0.7以上，但是盆地效果不佳。统计模型法是指利用影响降水分布变化的因子建立其与降水量的关系，从而得到降水量的分布函数(孙佳等，2011)。杨青等(2007)和杨扬等(1995)利用DEM数据，结合自然正交分解、多元回归、梯度距离平方反比法计算开都河流域的年面雨量序列。

本文拟利用对我国区域气候有着较好模拟能力的RegCM3模式(鲍艳等, 2006; 屈鹏等, 2009)对开都河流域2000—2006年的夏季气候进行模拟，并结合DEM数据对模拟结果进行修正，以探讨流域夏季面雨量的变化趋势与地表径流的关系及其影响机制。其中2006年的模拟数据不参与模型的建立，仅用于验证模型的适用性。

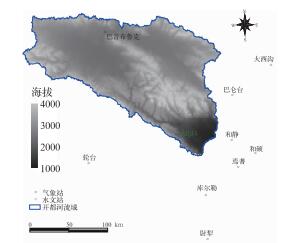
1 研究区概况

开都河流域位于新疆巴音郭楞蒙古自治州境内，天山南麓，地理坐标介于41°47′~43°21′N、82°58′~86°55′E之间。开都河源于新疆维吾尔自治区天山南麓焉耆盆地北缘，属于雪冰融水和雨水混合补给的河流，作为天山南坡水量最丰富的河流之一，既是新疆巴音郭楞蒙古自治州生态环境建设、农业灌溉、发电、排污和地下水补给的主要水源，又是博斯腾湖天然调节水库的源泉。开都河多年平均出山径流量为34.8×10⁸ m³(1956—2004年)，占博斯腾湖流域总径流的近85%，是博斯腾湖最主要的补给水源，其径流量的变化对于博斯腾湖具有重要影响。开都河流域图以及水文站点分布见图 1。由图可以看出开都河流域的地形是西北高，东南低，由西北向东南倾斜。流域最低海拔1000 m，最髙海拔4000 m，流域底部地势平坦，周围高山环绕，全流域可划分为三段：北部源头天山地及山间平原区，中游河段高山峡谷地区和下游河段山前冲积扇及绿洲平原区。

2 模式简介及试验方案设计 2.1 模式简介

本文采用的RegCM3模式是由意大利国际物理理论中心所研制，采用MM5动力框架，垂直方向为σ坐标，水平方向采用Arakawa-Lamb B型交错网格，主要参数化方案包括：辐射方案、陆面过程、行星边界层方案、积云对流方案、大尺度降水方案以及气压梯度方案。

2.2 模拟方案设计及检验方法

模拟选用Lambert投影，模拟的区域中心位于41°N、86°E，水平分辨率取为50 km，水平格点数为56×50格点，模拟区域包括整个新疆及周边地区。模式垂直分层为18层，模式顶层高度为100 hPa，时间积分步长为150 s。行星边界层方案采用Holtslag方案，侧边界条件采取指数松弛方案以及常规方法的气压梯度方案，积云对流参数化方案采用Kuo方案。模式运行所需用的输入数据有地形数据、陆地类型数据、海洋表面温度SST数据以及天气再分析数据。其中地形和陆地类型数据分别采用美国地质勘测局的GTOPO30和GLCC；天气再分析数据采用NNRP1资料，数据包括气温、高程、高程偏差、经向风、纬向风等，用作初始场和侧边界强迫；SST数据用的是美国国家海洋大气管理局(NOAA)提供的1°分辨率的最优插值海洋表面温度的周分析资料。模拟的积分时段为2000—2006年，从每年的5月1日00时开始到9月1日00时结束，分析结果选取每年的6—8月的输出结果作为开都河流域研究数据。

为了能够客观地分析模式对于温度以及降水的模拟能力，将模式模拟结果与站点所在位置的相应气温和降水模拟数据输出，与站点实测温度、降水数据进行对比分析。对模拟结果的修正资料DEM来自国际数据服务平台下载的ASTER GDEM数据，分辨率为30 m。为了与后面计算的面雨量的空间分辨率一致，将其重采样至1 km。计算得到的面雨量验证数据为大山口水文站的径流量数据。

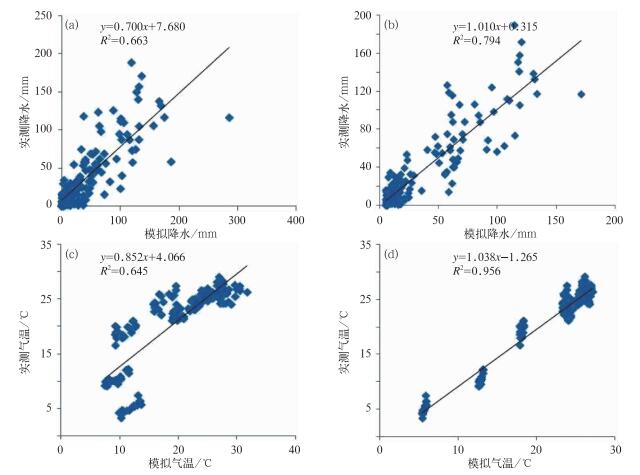
3 模拟结果与分析

表 1是6—8月月降水总量和月平均气温站点实测值与模拟值R²值(样本数27)，可以看出模式对于降水以及气温的模拟效果较好，R²均在0.6以上。影响气温和降水分布与变化的因素很多，主要包括：海拔、坡度及坡向等，其中尤以海拔高度的影响最显著(赵成义等，2011)。于是考虑利用这9个站点，根据海拔高度、月降水总量和月平均气温的实测值以及模拟值分别建立气温及降水的二元线性回归方程，并根据拟合的方程对模拟值进行修正(图 2)。为了验证拟合方程的适用性，这里仅使用2000—2005年6—8月的月降水总量、月平均气温的实测值和模拟值以及海拔高度值分别进行气温及降水方程的拟合，2006年的数据用于方程的验证。拟合降水的二元线性回归方程为：

$ {y_p} = 0.026{x_1} + 0.341{x_2} - 18.25 $

(1)

式中，x₁为站点对应的海拔高度值，x₂为模拟值，y_p为修正后的降水模拟值。方程显著性水平Sig值=0.000 < 0.05，表明方程显著，所建方程有效。图 2b是经过二元回归方程修正后的2000—2005年9个站点6—8月降水总量模拟值与实测值(162个样本)的R²值，R²达到了0.794，相比修正之前有了明显提升。同样，对月平均气温进行拟合，其二元线性回归方程为：

$ {y_t} = 0.149{x_3} - 0.007{x_4} + 28.64 $

(2)

式中，x₃为站点对应的气温模拟值，x₄为海拔高度值，y_t为修正后的气温模拟。方程显著性水平Sig值=0.00 < 0.05，表明方程显著，所建方程有效。图 2d是经过二元回归方程修正后的月平均气温模拟值与实测值(162个样本)的R²值，R²达到了0.956，相比之前有了明显提升。为了验证拟合方程的有效性，分别利用拟合的降水、气温方程对2006年的模拟值进行了修正，修正后的降水与气温的模拟值与实测值的R²分别为0.88和0.97，预测结果较好，拟合的方程有一定的预报性。表 2为2000—2006年各年经过二元回归方程修正后的模拟值与实测值的R²值，由表可以看出修正后的模拟值与实测值的相关关系均得到了提升，降水的R²值达到了0.8以上，气温的R²值在0.95以上。正由于耦合了对气温和降水分布有重要影响的高程，使得经过修正后的模拟的月降水总量以及月平均温度能够更好地刻画对应物理量的时空分布。

4 开都河流域面雨量、径流量以及水位的变化关系

博斯腾湖既是开都河的尾闾，又是孔雀河的源头，兼有开都河来水的水资源调控、孔雀河流域农田的灌溉、工业及城乡用水和流域生态保护等多种功能，在水资源十分珍贵的南疆有着十分重要的地位。对1980—2006年博斯腾湖水位分析可知，博湖水位多年平均值为1046.7 m，自1987年达到历史最低值1045 m后开始持续增长，在2002年达到了1049 m的历史水位高程，高于多年平均值2.3 m，这为塔里木河下游应急输水以及塔河下游供水提供了极大的便利，但是其后开始迅速下降，到2006年其水位仅为1046.6 m，下降了2.4 m，这对塔里木河输水以及农田灌溉等造成了一定的影响。因此分析气候变化对博湖水位变化的影响对于干旱区水资源的利用有着重要意义。

对开都河流域历年夏季径流量进行分析：根据1956—2006年大山口水文站的夏季径流量可知，其51年平均夏季径流量为15.8×10⁸ m³，自1974年达到51年的低值9.8×10⁸ m³后开始波浪式上升，2000年其夏季径流量达到25.6×10⁸ m³，其后迅速下降，2001年夏季径流量为16.7×10⁸ m³，减少了8.9×10⁸ m³。2002年又开始迅速回升，达到51年的最高值31.2×10⁸ m³，高于多年平均值97%，是1974年夏季径流量的3.2倍，而后又开始迅速下降，2005年其径流量仅为13×10⁸ m³，相对于2002年减少了58%，2006年开始小幅上升达到16.3×10⁸ m³。通过上述分析可以得知：2000—2006年开都河夏季径流量的变化与博湖水位变化趋势一致，博斯腾湖水位的变化主要由开都河径流量变化导致，因此研究开都河夏季径流量的变化对于研究博湖水位变化有着重要的意义。

将模式模拟的覆盖开都河流域的降水、地面2 m气温模拟值输出，并根据式(1) 和(2) 分别对其进行修正。其中海拔高度数据由国际数据服务平台下载的ASTER GDEM数据，分辨率为30 m，为了与面雨量空间分辨率一致，将其分辨率重采样至1 km。得到修正后的模式模拟的格点值，由于其分辨率为50 km×50 km，利用反距离加权插值法将其插值到1 km×1 km，并利用流域边界对其裁切，然后对流域内所有的格点面雨量求和，得到整个开都河流域的面雨量。

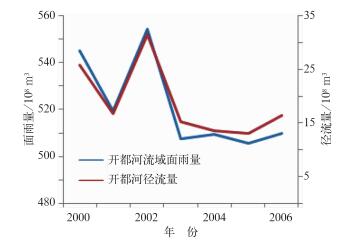
利用大山口水文站的夏季径流量数据对开都河流域面雨量进行验证。图 3为计算得到的开都河流域夏季面雨量与开都河夏季径流量时间变化序列，R²达到0.97，面雨量与径流量的变化趋势相同，在2001和2003年有2个明显的低值，在2002年径流量达到高值，2006年径流量略有回升。影响径流变化的主要因素有气候因素以及人类活动，由于开都河流域位于高海拔的山区，无显著的人类活动，其径流量的变化主要由降水以及冰川融雪所致。有报告指出在全球气候变化背景下，中国地区年平均气温呈现增高趋势，升温幅度约为0.5~0.8℃(丁一汇等，2006)。气候变暖使得自然生态系统受到严重影响，继而影响区域内的水循环和径流变化，因此主要依靠山区降水以及冰川融雪补给的开都河流域可能会受到这一变化的影响。

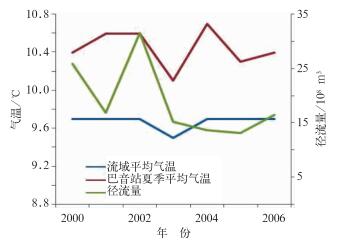
为了反映气候变化对开都河流域夏季径流量变化的影响，对开都河流域径流量、面雨量以及平均气温进行相关分析。结果表明：流域平均气温与径流量的相关系数为0.24，面雨量与径流量的相关系数为0.98，可以看出与气温相比面雨量和径流量的相关性较大，这在一定程度上说明面雨量是影响开都河夏季径流量变化的主要因子。为了进一步阐述气温与径流的关系，图 4给出了巴音布鲁克站与大山口径流量以及模拟的开都河流域平均气温的变化趋势图，可以看出模拟的2000—2006年开都河流域夏季平均气温，除了2003年比其他年份温度偏低0.2℃外并没有明显变化，与巴音布鲁克气象站夏季平均气温的相关系数为0.73，有较好的一致性。对巴音布鲁克站点的夏季平均气温与夏季径流量进行相关分析，相关系数为0.25，除了2003年气温与径流量同时达到低值，以及2006年的小幅提升外，其他年份并无明显的一致性，如2001年气温有了回升而同期径流量却减少，2002年径流量达到高值但是气温相对于2001年并没有变化，2004年气温达到7年中的高值而径流量却持续减少。由此可以看出，在流域平均气温变化不大的情况下，2000—2006年开都河流域夏季径流量的变化主要受到降水量的影响；而在气温与降水量同时减少的情况下将会导致流域径流量的减少。为了进一步研究气温与降水的变化对开都河径流量变化的影响，利用2000—2005年开都河面雨量、平均气温以及径流量建立二元线性回归方程，2006年的数据来验证拟合方程的适用性，拟合的方程为：

$ {p_k} = 0.372{y_k} - 11.05t - 68.56 $

(3)

式中，p_k为开都河流域面雨量(单位：10⁸ m³)，t为开都河流域平均气温(单位：℃)，y_k为开都河夏季径流量(单位：10⁸ m³)，拟合方程的R²达到0.994，方程显著性水平Sig值=0.001 < 0.005，表明方程显著，所建方程有效。根据方程预测的径流量与实测径流量的R²达到0.97，方程对于径流量的变化有着一定的模拟能力。由拟合方程计算的2006年径流量为：13.98×10⁸ m³，与实测径流的相对误差为14.2%，方程具有一定的预测性。拟合的二元回归方程的面雨量、平均气温的标准化回归系数分别为1.031和-0.119。标准化回归系数就是去除方程中自变量和因变量的度量单位的影响，使之“统一标准”，通过比较标准化回归系数能够更有效地分析各自变量的地位和作用。由标准化系数可以看出气温对于径流的贡献呈现负值，究其原因有可能是由于20世纪80年代以来开都河流域山区气温的持续升高(陶辉等，2007)，这势必会影响到流域内的冰川、积雪的分布面积。冰川面积减少，从而造成温度上升但冰川径流量没有相应增加的情况。有报告表明近年中国西部冰川变化多表现出较明显的退缩趋势(李忠勤等，2003)，根据巴音布鲁克气象站的气温资料指示，20世纪80年代中后期至2000年开都河流域山区温度较往年有所上升，温度的升高将导致山顶冰川融雪增加，冰川面积减少。对温度敏感的小冰川将大大减少，致使开都河流域夏季径流量随着温度增加而增加的关系减弱。孙占东等(2010)指出1984—2000年流域山顶冰川面积近消退40%。此外，对博斯腾湖流域的蒸散研究表明流域蒸散的年内变化呈单峰格局，7月最高，夏季的地表蒸散量占全年总蒸散量的48.10%，且夏季蒸散与降水、气温都存在明显的正相关性(徐永明等，2012)，因此在气温升高的同时，流域的蒸散量也有所提高，这可能是导致气温标准化回归系数呈现负值的又一原因。

5 结论与讨论

利用区域气候模式RegCM3对2000—2006年开都河流域夏季面雨量进行了数值模拟研究，并对其模拟能力进行了分析，得出以下结论。

(1) 通过模式模拟结果与站点实测值的对比可以看出，模式基本能够再现开都河流域的气温、降水空间分布特征，R²均在0.6以上。通过DEM数据、2000—2005年的实测值与模拟值拟合的二元线性回归方程对其模拟值进行修正之后，模拟的气温以及降水能力明显提高，模拟的降水与实测值R²达到0.8以上，气温在0.95以上。为了验证方程的有效性，根据拟合的方程对2006年的模拟值进行了修正，修正后的气温和降水值的R²分别为0.97和0.88，说明了该方法在开都河流域进行降水与气温估算的可行性。

(2) 利用修正后的模拟值对开都河流域夏季面雨量进行了估算，结果表明计算的面雨量与开都河实测径流量变化趋势基本一致，R²达到0.9以上。夏季径流量的变化与面雨量的变化有着十分密切的关系，降水是影响开都河夏季径流量变化的主要因子。而气温对于径流呈现负贡献的原因可能是由于20世纪80年代中后期至2000年开都河流域山区温度的持续升高导致山顶冰川融雪增加，冰川面积减少。对温度敏感的小冰川大大减少，致使开都河流域夏季径流量随着温度增加而增加的关系减弱。此外，气温的升高也会导致流域的蒸散量的提高，这可能是导致气温呈现负贡献的又一原因。