在现代气象观测中,特别是在突发性、灾害性天气的监测预警中,天气雷达发挥着越来越重要的作用。近年来,国内外众多学者对多普勒天气雷达的探测性能做出了大量的分析研究,可以看出其对中小尺度灾害性天气的监测和预报具有较高的准确率(Douglas et al,2007;张沛源等,2008;丛芳等,2010;Jameson,1989;李柏等,2013;张亚萍等,2013)。但是现阶段投入业务使用的多普勒天气雷达主要使用速调管等体积较大的大功率微波电子管作为发射机。而对设备本身体积和重量有限制的天气雷达如车载、机载或相控阵雷达,其发射机则只能采用体积小、重量轻的固态发射机。采用固态发射机的天气雷达又被称为全固态天气雷达,其发射机峰值功率往往较小(古志强,2001)。在此条件下为了获得较好的探测距离,则需要增大脉冲宽度来提高发射的平均功率,进而提高雷达的探测距离和探测能力。但宽脉冲的发射会大大降低雷达的距离分辨力,这成为全固态天气雷达信号处理必须解决的问题(翟庆林等,2007)。脉冲压缩技术因其在雷达发射机峰值功率受限的情况下,能有效解决目标距离分辨力与探测距离之间的矛盾,从而被广泛的应用到雷达信号处理中(吕幼新等,1993;Cho,2006)。但是,脉压后信号过高的旁瓣会淹没附近弱目标的主瓣,导致气象信息的缺失,并可能影响到预报的准确性。因此,旁瓣抑制的效果对于提高全固态天气雷达弱目标的检测能力来说十分重要(张子良等,2008)。
经典窗函数的加权处理是抑制旁瓣常用的方法。针对采用线性调频信号的脉冲压缩体制雷达,本文对在旁瓣抑制处理中采用不同广义余弦窗函数的脉压信号处理结果进行了分析,对其产生的旁瓣抑制效果进行了理论仿真,最后将广义余弦窗加权方法运用到全固态天气雷达的外场试验中,绘制出多幅天气目标反射率因子回波图,并结合多普勒天气雷达的探测数据分析了不同广义余弦窗对弱目标探测的影响。
1 脉冲压缩技术脉冲压缩技术是现代雷达的一项重要技术。线性调频(Linear Frequency Modulation,LFM)信号因具有匹配滤波器对其回波信号多普勒频移不敏感的特性而被经常应用到脉冲压缩体制雷达之中。雷达发射机发射频率或相位调制的宽脉冲,通过提高发射平均功率来获得较大的探测距离。在接收端,脉冲压缩处理系统将接收到的回波进行脉冲压缩,得到等效于窄脉冲回波的数据,以此来提高雷达的距离分辨力(O’Hora et al,2005)。但是,脉冲压缩输出的信号并非理想单一的脉冲,同时还存在一些不利于数据处理或观测的旁瓣,即距离旁瓣。在无加权网络时,LFM信号脉压处理后主旁瓣比(ratio of main lobe and side lobe,RMS)仅为13. 2 dB,而过低的RMS将导致很多弱气象目标回波信息的丢失。因此,提高LFM信号旁瓣抑制的效果是提升气象雷达弱目标探测能力的关键。
对于气象雷达而言,由于气象回波的信息量较大,一般是在接收端中频级采用频率域加权技术来抑制旁瓣。在实际处理过程中,加权方法相当于引入失配滤波器,而加权函数则是为了满足时间旁瓣的要求而选定的。频域加权方法的原理如图 1所示,其中H(f)相当于旁瓣抑制滤波器(胡航,2004)。

|
图 1 抑制旁瓣的加权处理 Fig. 1 Block diagram of weighting processing for suppressing side-lobes |
文献(林茂庸等,1984)中一般采用下列的形式来表示加权函数
| $ H(f) = K + (1 - K)\cos{^n}(\frac{{\pi f}}{B}) $ | (1) |
式中,K、n为表示不同加权的系数。下面以一个加权网络为例,设线性调频脉冲经匹配滤波后,输出具有矩形频谱|U(f)|=$\sqrt {T/B} react(f/B)$的sinc波形,多普勒频移为0。如果信号又通过一个加权网络,其传输函数为
| $ H(f) = K + (1 - K)\cos{^n}(\frac{{\pi f}}{B})\\ = K + (1 - K)[\frac{{\cos (2\pi f/B) + 1}}{2}]\\ = \frac{{1 + K}}{2} + \frac{{1 - K}}{4}[{e^{j2\pi f/B}} + {e^{ - j2\pi f/B}}] $ | (2) |
则加权网络输出信号可由下式求得
| $ g(t) = \sqrt {\frac{T}{B}} \int_{ - B/2}^{B/2} {H(f)} = {e^{j2\pi ft}}df\\ = \sqrt {\frac{T}{B}} \mathop \smallint \nolimits_{ - B/2}^{B/2} \{ \frac{{1 + K}}{2} + \\ \frac{{1 - K}}{4}[{e^{j2\pi f/B}} + {e^{ - j2\pi f/B}}]\}{e^{j2\pi f/B}}df $ | (3) |
根据傅氏变换的线性性质和时延性质,可得到输出信号的表达式为
| $ g(t) = \sqrt {\frac{T}{B}} \frac{{1 + K}}{2}B[\sin(Bt)] + \frac{{1 - K}}{{2(1 + K)}} \cdot\\ \{ \sin c(Bt + 1) + \sin(Bt - 1)\} $ | (4) |
由式(4) 对几个主要性能指标进行计算:(1) 主瓣峰值与最大旁瓣之比(RMS);(2) -3 dB主瓣加宽系数;(3) 加权引起的信噪比损失(Signal-to-noise Ratio Loss,SNRL)。
| $ SNRL = 10\lg [\frac{{{{(\frac{{1 + K}}{2} \cdot B)}^2}}}{{B \cdot \frac{B}{8}(3{K^2} + 2K + 3)}}]\\ = 10\lg [\frac{{2({K^2} + 2K + 1)}}{{3{K^2} + 2K + 3}}] $ | (5) |
在脉压技术中,引入失配滤波器后,在旁瓣抑制的同时会导致输出信号主瓣变宽、电平降低,即窗函数加权法对旁瓣的抑制是以距离分辨力降低和信噪比损失为代价的(徐庆等,2001)。选择不同的加权函数,对脉压后波形的影响也不同,因此,对常用加权函数的特性进行分析是必不可少的。
2 广义余弦窗频谱分析及加权仿真在实际信号处理过程中,线性调频回波信号经脉冲压缩后得到具有矩形特性的频谱,而频谱的边缘跃变是旁瓣增大的主要原因,广义余弦窗的钟形结构对于平滑脉压信号幅度谱边缘的跃变具有很好效果,从而可以有效减小旁瓣,但同时会使主瓣展宽、信噪比损失增加。
2.1 不同的窗函数频谱特性比较广义余弦窗包括海明窗(Hamming)、汉宁窗(Hanning)、布莱克曼窗(Blackman)等,是LFM信号旁瓣抑制技术中常用到的加权窗函数。现给出广义余弦窗的通用形式:
| $ ind = (0:N - 1 )\times 2\pi (N - 1)\\ window = A - B\cos (ind) + C\cos (2ind) $ |
这些窗是频率为0、2π/(N-1) 和4π/(N-1) 的余弦曲线的合成,其中N为窗的长度,A、B、C为常数。根据它们的取值不同,可形成不同的窗函数,如:海明加权,A=0.54,B=0.46,C=0;汉宁加权:A=0.5,B=0.5,C=0;布莱克曼窗加权:A=0.42,B=0.5,C=0.08。
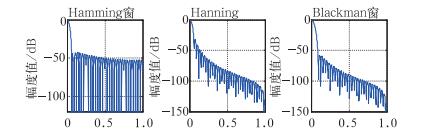
从图 2可以看出,布莱克曼窗函数的RMS最大,但主瓣却展宽最多;海明窗的RMS较汉宁窗更大,但它们的主瓣宽度是一样的。
|
图 2 几种常用窗函数的频谱特性比较图 Fig. 2 Comparison of spectral characteristics of several commonly used window functions |
通过几种常用窗函数频谱特性图的对比(丁美玉,2002),可以发现能量守恒使得频谱面积不变。对于加权函数而言,旁瓣降低,主瓣会展宽且幅度有所降低,这是一对矛盾。因此,对加权函数的选择需要通过计算机仿真的结果来进行具体讨论。
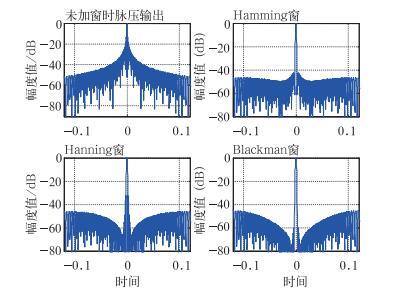
2.2 脉压信号加权的计算机仿真在仿真实验中,雷达发射信号的参数设为:脉冲宽度:T=150 μs,带宽:B=2 MHz,采样频率:8 MHz,仿真图如图 3所示。
|
图 3 加权前和分别采用3种常用的广义余弦窗加权的脉压输出信号仿真图 Fig. 3 Simulation diagrams of output signals before and after weighted by three generalized cosine windows |
对脉冲压缩旁瓣抑制效果评判的主要的性能指标有:最大主旁瓣比RMS/dB,信噪比损失SNRL/dB,-3 dB主瓣加宽系数等。表 1给出了未加权和3种不同的加权函数对脉压信号进行旁瓣抑制后输出响应的主要性能指标。
|
|
表 1 仿真实验所得广义余弦加权函数性能指标 Table 1 Performance of simulation results obtained by generalized cosine weighting functions |
通过对表 1各项数据进行比较可知,窗函数对脉压后信号的旁瓣抑制能力越强,则信号的主瓣展宽也就越大。因此,在进行加权滤波处理时,窗函数的选择问题实际是一个折衷考虑问题。对气象目标而言,若加权后脉压信号的主瓣展宽在一个可以接受的范围内,且信噪比损失较少(少于2 dB),主旁瓣比达到40 dB以上时,可以选择此类窗函数进行脉压旁瓣的抑制(Keeler et al,1995)。综合以上分析,在仿真实验里采用的广义余弦窗中,选择海明加权函数作为脉压加权网络所获得的仿真输出波形整体效果更好。
3 外场试验及分析为了检验在全固态天气雷达中运用不同的加权函数对脉压信号旁瓣的抑制效果,分析不同的窗函数对天气雷达获取弱目标能力的影响,需要进行晴空回波和弱降水回波的探测试验。
3.1 外场试验本文的试验是在成都信息工程学院的X波段全固态天气雷达和X波段的多普勒天气雷达上进行。全固态天气雷达试验参数:发射机峰值功率P1=50 W,脉冲宽度τ1=250 μs,带宽B=2 MHz,天线增益G=39 dB,波束宽度$\phi$=1.5°。多普勒天气雷达试验参数:发射机脉冲功率P2=75 kW,脉冲宽度τ2=0.833 μs。
试验所用的两部天气雷达均位于成都信息工程学院科教楼楼顶,相距约为49 m,雷达架设高度差约为2 m。因此,当多普勒雷达与全固态雷达天线扫描仰角相近时,探测获取的反射率因子数据可以近似比对。
试验1:数据采集时间:2012年7月12日17时30分,天气状况:晴,探测范围:150 km,全固态天气雷达天线仰角:1.5°,多普勒天气雷达天线仰角:1.4°。利用两部雷达对同一天气过程进行探测所得的回波强度对比如图 4所示。
|
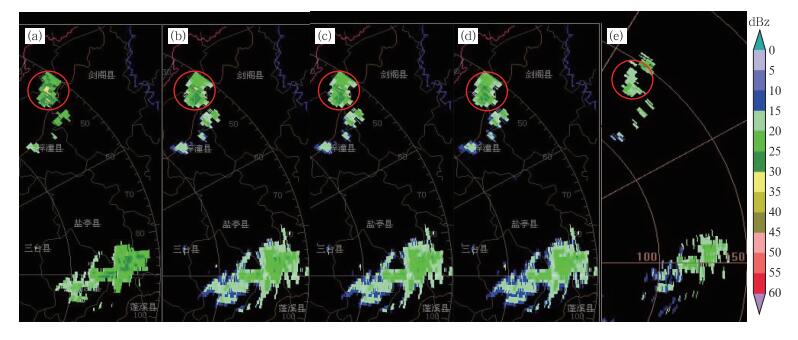
图 4 对2012年7月12日17时30分的晴空回波进行不同窗函数加权后的强度对比 (a)未加权, (b)海明窗加权, (c)汉宁窗加权, (d)布莱克曼窗加权, (e)多普勒天气雷达 Fig. 4 Comparison of different weighting window functions in clear-air echoes at 17:30 BT 12 July 2012 (a) no-window, (b) Hamming, (c) Hanning, (d) Blackman, (e) Doppler weather radar |
试验1采集的数据为晴空回波反射率因子,图中片状回波区域是强度范围为10~25 dBz的天气目标。其中前四幅图为全固态天气雷达探测回波图,图 4e为多普勒天气雷达探测回波图。就全固态天气雷达对目标的探测能力而言,四幅图都能明显显示红圈中140 km处的回波信号。未采用加权处理的图 4a中整体反射率因子强度偏高,且位于红圈中心的强反射率因子区域面积最大,辨析程度最高。海明窗(图 4b)和汉宁窗(图 4c)加权方式均能准确地探测到天气回波中心的强回波区域,且图 4b面积区域稍大。布莱克曼窗加权(图 4d)与以上两种方式相比,其探测获取的目标信号幅值偏小,对目标中心强回波的辨析度不佳。对比前四幅图的回波区面积可知,图 4b~4d中的回波信息总量明显多于图 4a。从结构上看,图 4b~4d中天气过程周边信息的显示都非常有层次,并能发现回波边缘的弱目标。而未采用加权的图 4a并没有显示回波边缘的弱目标信息。由此可以看出,采用窗函数加权方法的确能有效抑制回波的旁瓣电平,使强回波边缘的弱目标信息得以显现出来。
对比多普勒雷达(图 4e)与全固态雷达探测的回波图可知,天气回波的结构和位置大致是一致的,但全固态天气雷达回波图中目标边缘的弱回波信号较多,面积也更大。
试验2:数据采集时间:2012年7月14日15时33分,天气状况:中雨,探测范围:150 km,全固态天气雷达天线仰角:1.5°,多普勒天气雷达天线仰角:1.4°。图 5为利用两部天气雷达对同一降水过程进行探测时所获取的回波强度对比图。
|
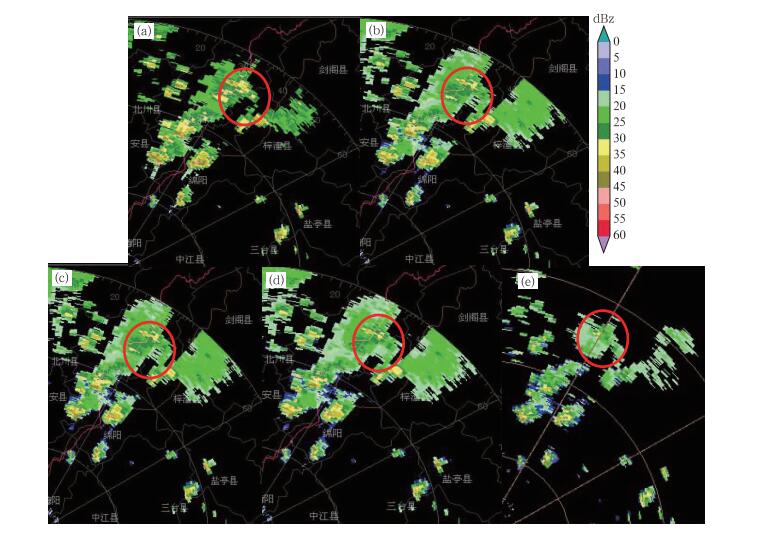
图 5 对2012年7月14日15时33分的降水过程回波进行不同窗函数加权后的强度对比 (a)未加权, (b)海明窗加权, (c)汉宁窗加权, (d)布莱克曼窗加权, (e)多普勒天气雷达 Fig. 5 Comparison of different weighting window functions in precipitation echoes at 15:33 BT 14 July 2012 (a) no-window, (b) Hamming, (c) Hanning, (d) Blackman, (e) Doppler weather radar |
试验2旨在将不同的窗函数加权方法运用到实际降水过程中,并进行回波强度的比较。通过对比图 5a与图 5b~5d可以看出,采用加权处理后得到的强度图能更完整地体现强天气目标附近的弱回波信息。因此,在降雨天气过程中采用窗函数加权方法可以使全固态天气雷达对弱目标的探测能力有较大提升。
然而,仅对以上两组试验的回波强度图进行直接比对很难直观地体现出不同的窗函数对弱目标探测能力的影响程度,所以还需要进一步对获取的回波数据做定量分析。
3.2 试验分析多普勒天气雷达获取的回波数据是现有的已被证明监测天气过程较为准确的数据(胡明宝等,2012)。以多普勒天气雷达数据作为标准,可分别对全固态天气雷达单个径向、整片回波区域的反射率因子强度和探测数据的一致性进行描述(杨金红等,2008;史锐等,2010)。
3.2.1 探测数据的一致性与准确性针对图 4与图 5中出现天气回波的径向进行定量分析,可分别绘制多普勒天气雷达和全固态天气雷达采用三种不同的窗函数加权处理时在回波区域单个径向上提取的反射率因子随距离变化图(图 6)。以多普勒天气雷达数据作为标准,对比全固态天气雷达在同一距离处探测获取的天气目标强度数据,可以看出图 6中的几条曲线形状与趋势相近,说明两部天气雷达探测获取的反射率因子具有较好的一致性,而试验2(图 6b)中多普勒天气雷达探测数据强度偏小,其原因可能是雷达标定计算中有偏差。
|
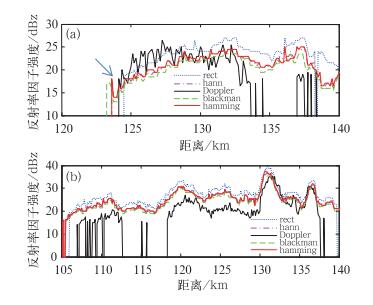
图 6 多普勒雷达与全固态雷达采用不同的窗函数的单个径向反射率因子强度对比图 (a)2012年7月12日, (b)2012年7月14日 Fig. 6 Contrast of single radial reflectivity factor intensity between Doppler radar and solid-state radar (a) 12 July 2012, (b) 14 July 2012 |
图 6a箭头所指处是多普勒雷达探测到的较强目标周围的弱回波信号,当全固态雷达未采用加权时,由于不存在加权带来的信噪比损失,因而其回波强度明显较采用加权处理之后更高。但与此同时,未进行加权处理的回波数据旁瓣过高、能量泄漏严重,从而导致了弱气象目标回波的丢失。加权后旁瓣电平降低,使得较强目标周围的弱目标信息得以显现,这进一步说明了窗函数加权处理对全固态雷达的重要性。由图 6可以看出,海明加权的回波强度均等于或高于其他加权方式。根据气象雷达方程(张培昌等,2010)和表 1可知,海明加权脉压信号的信噪比损失最小,探测准确性最佳。
3.2.2 探测数据的一致性与准确性分析图 5中整片降水回波,将两部雷达采集到的五组反射率因子数据进行统计描述如表 2和图 7。
|
|
表 2 雷达探测的反射率因子数据统计描述表 Table 2 Statistical description table of reflectivity factor |
|
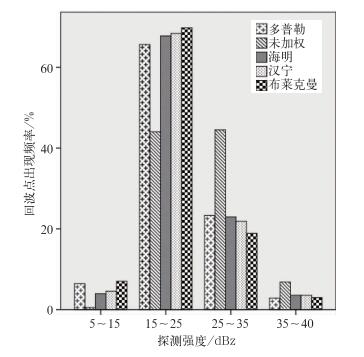
图 7 反射率因子强度的频率统计直方图 Fig. 7 The frequency statistics of reflectivity factor intensity |
气象目标不同于点目标,其探测目标是一个空间体积内分布的云雨粒子(陆静等,2010)。当对于同一天气过程的体目标进行探测时,由于两部雷达发射脉宽和发射机制的不同,使多普勒雷达在整片回波区域上能够获取到的回波点数明显要少于全固态天气雷达。
图 7中的回波点出现频率指的是在各个探测强度区域中回波点出现的次数与总回波点数的比值。从表 2和图 7可以看出未加权探测数据的均值、极大值和极小值都较其余几组数据较高,回波点在探测强度较高的区域有大量分布,而在5~15 dBz的弱回波区域几乎不能探测到数据。结合图 4的回波图和表 1中各项性能参数的指标进行分析可知,未加权时脉压信号RMS最小、信噪比损失最小,因此回波信号强度最强,与图 4a描述一致。布莱克曼加权探测数据的均值、极大值和极小值最低,在图 7的5~15 dBz弱回波探测区域中布莱克曼加权获取数据最多且最接近多普勒雷达的探测数据,这是由于其脉压信号RMS最大,抑制旁瓣的程度最大,使隐藏在高旁瓣下的弱回波得以显现,因此可以说布莱克曼加权对弱回波的探测能力较其他加权方式更强。但布莱克曼加权主瓣展宽较大,可能导致距离分辨力降低,进而影响观测。并且较大的信噪比损失使其在25~30 dBz和>35 dBz两个区域内的探测能力下降。海明和汉宁加权的探测数据在各个区域的分布均较为接近,其中海明加权在各个强度区域上反射率因子回波点出现的频率更加接近多普勒雷达的探测数据。
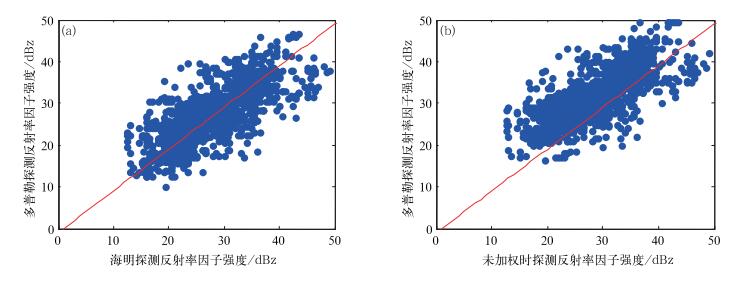
回波散点分布如图 8所示,图中黑色直线表示对角线。由图可知,采用海明加权处理的回波数据大量散落在对角线附近,说明海明加权的探测数据和多普勒雷达的探测数据具有一致性,而未加权时的反射率因子强度与多普勒雷达探测的强度差别较大,不能保证探测数据的一致性。
|
图 8 全固态雷达加权前后与多普勒雷达反射率因子强度对比散点分布图 Fig. 8 Scatter diagrams of radar reflectivity factor intensity detected by Doppler radar and solid-state radar |
结合图 4、图 7和表 1中各项性能参数的指标可以看出,海明与汉宁加权的信噪比损失较为接近,对于天气目标中心较强回波的探测能力相当。当目标强度范围大于25 dBz时,海明加权方式探测到的回波更接近多普勒雷达的探测数据。布莱克曼加权RMS最大,因而其对弱回波的探测能力更强,但其过大的主瓣展宽会导致距离分辨力降低,进而对天气过程的观测造成影响。
4 结论本文主要研究了将广义余弦窗运用于脉压旁瓣抑制处理中对弱天气目标探测产生的影响。在实际天气回波数据处理中,窗函数对脉压旁瓣抑制的效果越好,弱回波受到邻近强目标旁瓣的影响越小,其回波信息的层次也更分明,但相应的信噪比损失也会增大,从而使发现弱目标的能力减弱;同时过大的主瓣展宽会导致分辨力降低,使得成片的回波影响其周边弱气象目标的观测。
通过仿真和实际雷达数据的统计分析可以看出,海明加权函数能折衷各项性能指标,在其对旁瓣抑制效果较好的同时对距离分辨力和幅值的影响也最小,并且全固态雷达采用海明加权方式抑制距离旁瓣后获取的探测数据与多普勒雷达数据的一致性也较好。因此在脉冲压缩技术中采用海明窗加权方式后,对弱目标的探测效果更佳,在实际全固态天气雷达中应用时可以得到层次分明的回波结构,以及较完整的回波信息。
丛芳, 刘黎平, 2011. 新一代天气雷达与地面雨量资料的综合分析[J]. 气象, 37(5): 532-539. DOI:10.7519/j.issn.1000-0526.2011.05.003 |
丁玉美, 2002. 数字信号处理(第2版)[M]. 西安: 西安电子科技大学出版社, 318.
|
古志强, 2001. 全固态雷达发射机脉冲电源设计[J]. 现代雷达, 6(23): 80-83. |
胡航, 2004. chirp信号脉压旁瓣抑制方法研究[J]. 火控雷达技术, 33(3): 1-4. |
胡明宝, 赵景志, 夏文梅, 等, 2012. 双偏振多普勒天气雷达和CINRAD-SA对比分析[J]. 现代雷达, 34(1): 5-19. |
李柏, 古庆同, 李瑞义, 等, 2013. 新一代天气雷达灾害性天气监测能力分析及未来发展[J]. 气象, 39(3): 265-280. DOI:10.7519/j.issn.1000-0526.2013.03.001 |
林茂庸, 柯有安, 1984. 雷达信号理论[M]. 北京: 国防工业出版社, 214.
|
陆静, 陆洪涛, 孟博, 等, 2010. 对多普勒天气雷达的欺骗干扰方法分析[J]. 现代雷达, 32(2): 100-103. |
吕幼新, 向敬成, 陈辅新, 1993. 降低线性调频脉冲压缩信号旁瓣的方法[J]. 电子科技大学学报, 22(4): 344-349. |
史锐, 程明虎, 崔哲虎, 等, 2010. 长江流域多普勒雷达回波强度资料对比分析[J]. 气象, 30(11): 27-50. |
徐庆, 徐继麟, 黄香馥, 2001. 一种脉冲压缩信号旁瓣抑制方法[J]. 系统工程与电子技术, 23(5): 60-62. |
杨金红, 高玉春, 程明虎, 2008. 相控阵天气雷达与多普勒雷达的探测精度与探测能力对比研究[J]. 气象, 34(5): 44-52. DOI:10.7519/j.issn.1000-0526.2008.05.008 |
翟庆林, 张军, 付强, 2007. 线性调频脉冲压缩技术及其在雷达系统中的应用[J]. 现代电子技术, 14(1): 17-19. |
张培昌, 杜秉玉, 戴铁丕, 2001. 雷达气象学(第2版)[M]. 北京: 气象出版社, 499.
|
张沛源, 杨洪平, 胡绍萍, 2008. 新一代天气雷达在临近预报和灾害性天气警报中的应用[J]. 气象, 34(1): 3-11. DOI:10.7519/j.issn.1000-0526.2008.01.001 |
张亚萍, 张勇, 廖峻, 等, 2013. 天气雷达定量降水估测不同校准方法的比较与应用[J]. 气象, 39(7): 923-929. DOI:10.7519/j.issn.1000-0526.2013.07.013 |
张子良, 郑国光, 刘一峰, 2008. 相控阵天气雷达脉压距离旁瓣抑制研究[J]. 现代雷达, 30(5): 37-40. |
Cho J Y N.2006.Multifunction Phased Array Radar Pulse Compression Limits. ATC-327, Springfield:The National Technical Information Service. http://www.ll.mit.edu/mission/aviation/publications/publication-files/atc-reports/Cho_2006_ATC-327_WW-13781.pdf
|
Douglas E F, James F K, Dusan S Z, et al.2007.Update on the national weather radar testbed (phased-array).23rd International Conference on Interactive Information and Processing System (IIPS). San Antonio:Americ Meteor Soc, 15-20.
|
Jameson A R, 1989. The interpretation and meteorological application of radar backscatter amplitude rations at linear polarizations[J]. J A Ocean Tech, 6(6): 908-919. DOI:10.1175/1520-0426(1989)006<0908:TIAMAO>2.0.CO;2 |
Keeler R Jeffrey, Hwang C A, 1995. Pulse Compression for Weather Radar[J]. IEEE International Radar Conference: 529-535. |
O'Hora Fritz, Bech Joan, 2005. Operational use of pulse compression in weather radar[J]. 32nd Conference on Radar Meteorology, P4R7. |
 2014, Vol. 40
2014, Vol. 40 