2. 解放军理工大学气象海洋学院,南京 211101;
3. 解放军93685部队,张家口 075000
2. College of Meteorology and Oceanography, PLA University of Science and Technology, Nanjing 211101;
3. No.93685 Unit of PLA, Zhangjiakou 075000
过去的几十年中,随着计算机性能的不断提升,数值天气预报取得了长足的进步与发展,预报的准确度在不断提高。现今,几乎所有的业务部门都将数值预报的结果作为制作天气预报的重要依据。然而数值预报的发展却遇到了瓶颈,Lorenz(1963)指出初始场的微小误差随着模式积分时间的增长,预报结果会与真实大气状态存在一定偏差, 而对于初始场,由于人为的、仪器的、观测网络覆盖率及同化和客观分析方法的影响总会存在误差,永远只能是实际大气的一种近似值,所以,即使模式非常完美,初始值的微小误差也会对预报结果产生较大影响,这就从根本上指出了数值天气预报在本质上是非确定性的。因此用众多可能的预报状态的一种来描述未来大气的状态是不够科学的,更合理的方法是以概率的形式来认识大气预报状态,而对所有可能的预报状态及这些预报状态的概率分布进行预报,这种预报方法就是集合预报(刘家俊等,2010), Lorenz(1965)奠定了数值集合预报的理论基础。
集合预报的基本思想是承认当今所用的初始场是存在误差的,在实际预报中要考虑到这种误差,所以构建出一组关于初始场的大气相空间的概率分布函数(Probability Density Function, PDF)来反映大气真实初值的不确定性。经典的集合预报是在确定性预报的初始场上施加一些能反映初值不确定性的小扰动,用加扰动的初值制作一系列预报,把这些预报通过平均以减少各自决定性预报的误差,从而使预报的误差更小(郑峰,2008)。集合预报在国际上被公认为是最具发展前途的,解决确定性数值预报“不确定性”问题的新一代随机动力预报理论和方法(牛震宇等,2006)。杜钧等(2010)指出集合预报并不仅仅是一种新的技术和方法,它的方法和理念将使整个数值预报体系进入一个新纪元。世界气象组织(World Meteorological Organization, WMO)将集合预报列为未来数值预报的主要发展战略方向之一。
暴雨是中尺度灾害性天气,目前在暴雨数值预报中由于初值和物理过程的不确定性使得单一确定性预报对暴雨的预报存在较大误差。作为经典集合预报方法的初值集合预报是解决暴雨预报不确定性的一个很好的方法(牛震宇等,2006)。Brooks等(1996)利用初值集合预报方法对一次强对流天气进行集合预报试验,取得了较好的效果,陈静等(2005)提出了异物理模态法推动了暴雨集合预报的发展,Hamill等(1997)、Du等(1997)、谭燕等(2008)利用初值集合预报方法进行了集合预报试验,认为初值集合预报可以在一定程度上提高暴雨预报的准确率。
综观国内外对初值集合预报的研究(Leith,1974;Hoffman et al,1983;Toth et al,1993;1997;Buizza et al,1995;Houtekamer et al,1995;Bishop et al,2001;Majumdar et al,2002;Wang et al,2003;田伟红等,2008;纪永明等,2011;任志杰,2011;夏凡等,2012;韩焱红等,2013),大都是关于大气变量初始场的不确定性对集合预报影响的研究,很少有关于陆面变量(参数)初始场的不确定性对集合预报影响的研究。事实上研究已经证实陆面过程或陆面参数对暴雨等短期天气有重要影响。Pielke(2001)指出陆面特性量对大气的影响尺度可从单个雷暴尺度到全球尺度。张朝林等(2007)在MM5模式中引进精细下垫面信息对北京一次24 h暴雨进行模拟,结果表明改进之后的模式对模拟降水的中心位置及强度有重要影响。Tryhorn等(2008)利用MM5模式研究了澳大利亚阿尔卑斯郡大火后地表状况改变对随后该地区暴雨及洪水的影响,结果表明大火之后地表状况特别是地表反照率和土壤水分含量的减少对该地区随后的暴雨有重要影响。曾新民等(2012)用WRF3.1模式的4个陆面方案对2003年6月下旬10个暴雨个例进行模拟并对其影响机理进行了分析,结果表明不同陆面过程可以从不同空间尺度、不同程度上影响暴雨天气。而目前中尺度模式中陆面变量(参数)大多是由精度或分辨率不高的卫星遥感资料获得,缺乏实测的基础,这就使得模式中输入的陆面变量(参数)初始值存在较大偏差(曾新民等,2009)。基于此,本文利用WRF3.2.1模式,研究短期暴雨天气对陆面变量(参数)初始场扰动的敏感性,以及基于上述初始扰动的集合预报对改进暴雨预报的影响。本文结果为初值集合预报的改进提供了一种新方法,对提高暴雨数值预报的水平具有重要的现实意义。
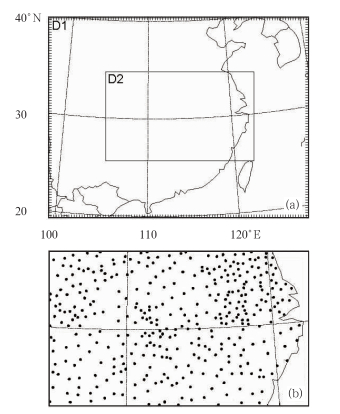
1 试验方案设计及暴雨天气过程 1.1 模式及试验方案设计这里选用的模式为WRF3.2.1版,WRF是近年来由美国环境预报中心(National Centers for Environmental Prediction, NCEP)等多家科研机构联合开发出的下一代中尺度模式,现已广泛地应用于各种研究与业务预报中。这里选用的物理方案主要包括WSM3微物理方案,RRTM长波辐射方案,Dudhia短波辐射方案,YSU行星边界层方案,Betts-Miller-Janjic积云对流参数化方案,NOAH陆面过程方案。如图 1所示,本试验采用双向两重嵌套网格,区域中心为(30°N、113.5°E),大区域的格点数为101×78,小区域的格点数为172×103,水平格距分别为30和10 km,垂直分辨率为不等距31层,模式顶气压50 hPa。模式的初始场采用NCEP再分析资料生成,积分时间从2007年5月31日0000 UTC至2007年6月1日0000 UTC共24 h积分,大小区域积分时间步长分别为180和60 s。如不作特别说明, 下面分析中均为对D2区域的模拟结果进行分析。
|
图 1 模式嵌套区域及观测站点分布 (a)模式嵌套区域, (b)区域D2内参与评估的观测站点分布 Fig. 1 Model domain and distribution of meteorological stations used for assessment (a) model domain, (b) distribution of meteorological stations used for assessment in domain 2 |
本文选取的陆面变量为土壤湿度(Soil Moisture, SMO)、土壤温度(Soil Temperature, TSL),陆面参数为植被覆盖率(Vegetation Fraction, VEG), 对上述变量(参数)逐一叠加初始扰动,每个试验以各自的英文缩写加数字命名,一个变量(参数)的扰动试验视为一个子集,例如土壤湿度SMO初值扰动试验命名为SMO子集,SMO15表示该子集的第15个集合成员。
在初始扰动的叠加上,本文认为插值到模式格点上的变量或参数的值都存在一定误差,同时对插值到两重嵌套区域每个格点上的变量(参数)的初始值采用蒙特卡罗(Monte Carlo Forecasting, MCF)法进行随机扰动。由于蒙特卡罗法生成的初始扰动集合成员间的离散度较小,所以为了增加集合成员之间的离散度,本文每个变量(参数)做30个扰动试验。
陈静等(2005)指出如何确定模式变量的最大振幅是初值扰动方案的一项重要内容,由于陆面变量(参数)在中国区域缺乏实测值,难以确定初始误差的最大扰动振幅。本文在初始误差的处理上认为NCEP资料相对较为准确,每个格点上有误差,但初始误差不会超过该格点的值。叠加初始扰动时扰动振幅取模式网格点上SMO、VEG值的5%、10%、20%、30%、40%做敏感性试验,认为扰动振幅值取格点值的20%较为合适。本文取每个格点值的20%作为该格点的扰动振幅,扰动振幅乘以[-1, 1]之间均匀分布的随机数作为其初始扰动叠加在初始场上生成新的初始场定义如下:
| $ \begin{array}{l} VARN\left({mx, my, ml} \right) = VARN\left({mx, my, ml} \right)\left[ {1{\rm{ + }}} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {0.2 \times random\left({mx, my} \right)} \right] \end{array} $ |
可以看出相当于对每个格点上的SMO、VEG的值乘以[0.8-1.2]范围内的一个均匀分布的随机数做为该格点上新的初值,和Buizza等(1999)对净的强迫项乘以[0.5-1.5]内均匀分布的随机数相比,本文并没有高估初始扰动的误差。
对于土壤温度TSL,由于其温度的值较大,对网格点上的TSL值乘以0.5%、1%、1.5%、2%该格点的扰动振幅做敏感性试验,认为扰动振幅取格点值的1%较为合适。扰动振幅乘以一个[-1, 1]之间均匀分布的随机数作为其初始扰动,加在初始场上生成新的初始场,定义如下:
| $ \begin{array}{l} VARN\left({mx, my, ml} \right) = VARN\left({mx, my, ml} \right)\left[ {1{\rm{ + }}} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\rm{0}}{\rm{.01}} \times random\left({mx, my} \right)} \right] \end{array} $ |
其中VARN(mx, my, ml)为每个格点上的初值,由于陆面方案采用NOAH陆面方案,NOAH陆面方案是一个能预报4层(10、30、60、100 cm厚)土壤温度和湿度的模式,所以陆面变量为SMO、TSL时ml为4,为陆面参数VEG时ml为1;random(mx, my)为[-1, 1]之间均匀分布的随机数。
可以看出对于陆面变量SMO和TSL,在叠加初始扰动时,上下4层乘以同一个随机数,这样做的目的是使各层同比例的增长,使之更符合陆面变量的物理意义。同时在对陆面变量(参数)叠加初始扰动时根据各变量(参数)的物理意义对其扰动做出调整,例如SMO变量表示土壤湿度,其取值应大于0, 小于等于1,当某个格点上SMO的值为1时表示该地区为水体,该格点上的初值不叠加扰动,某格点上的土壤湿度扰动后大于1时,给其赋值为1;VEG表示植被覆盖率,其取值应大于等于0, 小于等于100%,所以对扰动后的值进行控制,当扰动后其值大于100%时给其赋值为100%。
1.2 暴雨过程2007年5月30日到6月3日,在冷暖空气的相互作用下,受低涡切变线影响,我国长江中下游及江南华南地区,自北到南发生了一次强烈的暴雨天气过程。5月31日到6月1日受锋面气旋云系及其尾部对流云团的影响,我国黄淮南部、江淮、江南中北部等地普降大到暴雨,较强降水区出现在对流比较旺盛的长江中下游地区(如图 2a)。该地区出现大范围的6 h降水量超过10 mm的区域,其中重庆北部出现6 h降水量达到60 mm的强降水,安徽安庆市31日晚到6月1日08时(北京时)市区降水量达163 mm,江西也出现了当年入夏以来的最强降水有8个县市出现了暴雨,5个县市出现了大暴雨。
|
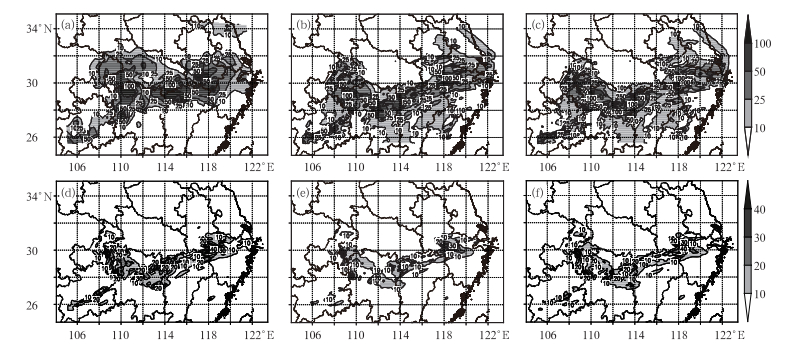
图 2 24 h累积降水(a, b, c)及离散度(d, e, f)(单位:mm) (a)观测, (b)控制试验, (c)SMO9, (d)SMO子集, (e)TSL子集, (f)VEG子集 Fig. 2 The accumulated precipitation in 24 h (a-c) and the divergence (d-f) (unit: mm) (a)observed, (b)CTL, (c)SMO9, (d)SMO ensemble, (e)TSL ensemble, (f)VEG ensemble |
由降水邮票图(图略)可以看出,各成员在降水的空间分布上和控制预报的结果(图 2b)较为相似,与实况(图 2a)符合较好,均较好预报出了长江中下游地区的强降水带,并且对29°N附近的3个强降水中心都有一定体现,同时可以看出各成员在预报强降水中心位置和区域细节上存在较大差异,降水在空间分布上对陆面变量(参数)初始扰动是敏感的。
图 2d、2e和2f给出了集合平均预报的离散度,离散度(Buizza et al,1998)为各扰动预报与集合平均预报之间的平均距离,其计算公式为:
| $ Spread{\rm{ = }}\sqrt {\sum\limits_{i = 1}^N {\frac{1}{N}{{\left({{f_i} + {f_0}} \right)}^2}} } $ | (1) |
式中,N为集合成员的个数,fi为每个扰动预报,f0为集合平均场。由图 2d、2e和2f可以看出,离散度的空间分布基本上和降水带的空间分布相似,整个雨带的离散度基本上在10 mm以上,这在一定程度上说明了各个成员的预报结果差别较大,降水对陆面变量(参数)扰动是敏感的,利用陆面变量(参数)扰动来构造集合预报,各成员能够反映出降水预报的不确定性。同时可以看出离散度的大值中心和24 h累积降水的大值中心相对应,降水越强其离散度越大,这反映了模式对暴雨中心的预报较差,在单一、确定性预报中模式对暴雨中心的预报结果可信性较小。
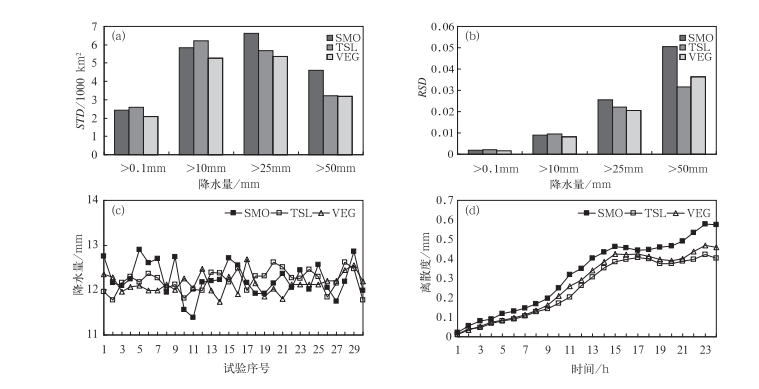
这里将降水分为小雨(0.1~9.9 mm)、中雨(10~24.9 mm)、大雨(25~49.9 mm)、暴雨(50 mm以上)4个量级,分别统计发生各量级以上降水的落区面积。由各量级降水落区面积的统计(图略)可以看出,陆面变量(参数)扰动可以导致各量级降水落区面积的较大差异。对于小雨以上降水的落区面积,SMO子集各成员落区面积最大偏差为10500 km2,相对于控制的试验的1312500 km2小雨以上降水落区面积,最大差异百分比为0.80%;TSL子集落区面积最大偏差为10200 km2,最大差异百分比为0.78%;VEG子集落区面积最大偏差为8400 km2,最大差异百分比为0.64%。同时可以看出随着降水量级的增大,降水落区面积的最大差异逐渐增大,对于暴雨量级以上降水落区面积,SMO、TSL、VEG 3个子集的最大差异百分比可达到21.42%、16.19%、15.61%。由于最大最小差异只能代表极值情况并不能代表整体的离散情况,图 3a和3b给出了各量级降水落区面积的标准差(STD)和相对标准差(RSD,标准差和平均值的比值),由图 3a可以看出3个子集在各量级降水上的标准差均较大,这说明陆面变量参数扰动可以导致各量级降水落区面积的较大差异,扰动对降水的范围和面积有较大影响。由图 3b可以看出降水量级越大,相对标准差越大,这说明陆面变量(参数)扰动对大量级降水的影响要大于对小量级降水的影响。
|
图 3 降水过程特征量:(a)24 h降水落区面积标准差(STD), (b)24 h降水落区面积相对标准差(RSD), (c)24 h降水区域平均, (d)逐时降水的离散度 Fig. 3 Characteristics of the rainfall process: (a) standard deviation of 24-h accumulated precipitation areas, (b) relative standard deviation of 24-h accumulated precipitation areas, (c) 24-h accumulated precipitation of area average, (d) hourly divergence |
如果比较单站的24 h累积降水量,可能会因偶然因素导致结果的较大偏差,所以这里选用区域D2内降水的平均值来衡量所选变量(参数)扰动对短期降水模拟的影响。由图 3c可以看出SMO子集的最大差异为1.52 mm,相对于控制试验的12.19 mm的区域平均降水,其最大差异百分比为12.47%;TSL子集最大偏差为0.84 mm,最大差异百分比为6.89%;VEG子集最大偏差为0.95 mm,最大差异百分比为7.79%。同时由标准差(图略)可以看出,SMO、TSL、VEG 3个子集区域平均降水的标准差分别为0.38、0.25和0.22 mm。这说明从整体上来说降水对陆面变量(参数)扰动是敏感的。
图 3d给出了逐时降水格点平均的离散度(王雨等,2007)为,其计算公式为:
| $ Spread\left(t \right){\rm{ = }}\overline {\sqrt {\sum\limits_{i = 1}^N {\frac{1}{N}{{\left[ {{f_i}\left(t \right) - {f_0}\left(t \right)} \right]}^2}} } } $ | (2) |
式中, “——”表示模拟区域内的格点平均,t表示预报时效,N为集合成员的个数,fi(t)为每个扰动预报,f0(t)为集合平均场。由逐时离散度的结果(图 3d)可以看出在前3 h的预报中陆面变量(参数)扰动对降水的影响较小,第5小时SMO子集预报降水的离散度可达到0.1 mm以上,TSL子集、VEG子集第7小时预报降水的离散度可以达到0.1 mm以上。这说明随着预报时间的增加陆面变量(参数)扰动对降水的影响在逐渐显现出来,总体上来说陆面变量(参数)扰动在6 h左右即可对降水有显著影响。由3个子集24 h累积降水格点平均的离散度(图略)可以看出,SMO子集、TSL子集、VEG子集的离散度分别为3.64、3.01和3.14 mm,而集合平均的24 h累积降水量为12.54 mm,这说明总体上来说陆面变量(参数)扰动对短期降水有重要影响,在构造集合预报系统中考虑陆面变量(参数)初始值的不确定性是必要的。
2.2 评估参数结果 2.2.1 ETS评分结果为了评估各变量(参数)扰动对降水空间分布上的影响,这里将模式模拟区域D2内的379个有效发布站的24 h降水状况作为检验对象,统计降水的ETS评分(Equitable Threat Score)(王雨等,2007)。其计算公式如下:
| $ ETS = \frac{{{N_A} - CH}}{{{N_A} + {N_B} + {N_C} - CH}} $ | (3) |
| $ CH = \frac{{\left({{N_A} + {N_B}} \right)\left({{N_A} + {N_C}} \right)}}{{\left({{N_A} + {N_B} + {N_C} + {N_D}} \right)}} $ | (4) |
式中,NA为预报发生降水且实况也发生降水的站数,NB为预报发生降水但实况没有发生降水的站数,NC为没有预报出降水但实况有降水的站数,ND为没有预报出降水且实况也没有降水的站数。
ETS评分又称公平的TS评分,考虑了随机降水概率对评分的影响,消除了参加统计站的多少对TS评分的影响,理想的ETS评分为1,取值范围-1/3~1,0表示没有预报技巧。
这里同上将降水分为小雨、中雨、大雨、暴雨4个量级,分别统计发生各量级以上降水的ETS评分情况。
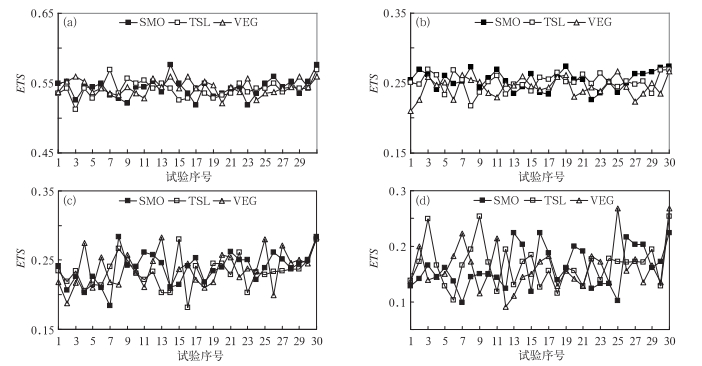
由图 4可以看出对于0.1 mm以上降水,SMO子集ETS评分的最大差异为0.058,TSL子集的最大差异为0.057,VEG子集最大差异0.038,对于10 mm以上量级的降水3个子集的最大差异在0.050左右,而对于25和50 mm以上量级降水3个子集的最大差异分别在0.10和0.18左右。由ETS评分标准差的结果(图略)可以看出,对于0.1和10 mm以上量级降水,3个子集的ETS评分的标准差在0.12左右,对于25和50 mm以上量级的降水则在0.22和0.35左右,可见陆面变量(参数)扰动对各量级的降水均有较大影响,对大量级降水的影响要大于对小量级降水的影响。由相对标准差结果(图略)可以看出,对于0.1和10 mm以上量级的降水,3个子集ETS评分的相对标准差在0.02和0.05左右;对于25和50 mm以上量级的降水,3个子集的相对标准差则在在0.09和0.22左右,总体上来说随着降水量级的增大3个子集的ETS评分的相对标准差在增大。由以上分析可以看出,陆面变量(参数)扰动对降水有较大影响,且扰动对大量级降水的影响要大于对小量级降水的影响。
|
图 4 ETS评分结果(a)>0.1 mm, (b)>10 mm, (c)>25 mm, (d)>50 mm Fig. 4 Equitable Threat Score (a) > 0.1 mm, (b) > 10 mm, (c) > 25 mm, (d) > 50 mm |
为评估各变量(参数)扰动对24 h累积降水的整体影响,这里还采用均方根误差(RMSE)和空间相关系数(CORR)来评估扰动对降水的影响,其计算公式为:
| $ RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left({{M_i} - {O_i}} \right)}^2}} } $ | (5) |
| $ CORR = \frac{{\sum\limits_i^N {\left( {{M_i} - \bar M} \right)} \left( {{O_i} - \bar O} \right)}}{{\sqrt {{{\sum\limits_i^N {\left( {{M^i} - \bar M} \right)} }^2}} \sqrt {{{\sum\limits_i^N {\left( {{O_i} - \bar O} \right)} }^2}} }} $ | (6) |
式中,N为总站点数,Mi为第i站预报降水,Oi为第i站实况降水,M为预报降水的平均值,O为实况降水的平均值。
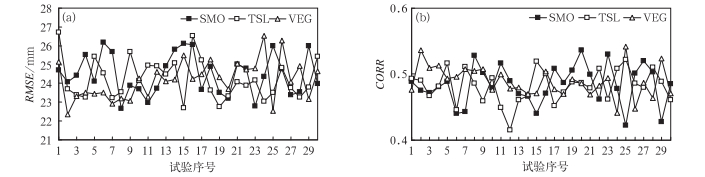
陆面变量(参数)扰动可以导致24 h累积降水均方根误差和空间相关系数的较大差异(图 5)。SMO、TSL、VEG子集的均方根误差的最大差异分别为3.53、3.99和4.17 mm,均方根误差的标准差(图略)分别为1.08、1.05和1.02 mm;空间相关系数的最大差异分别为0.114、0.107和0.100,空间相关系数的标准差(图略)分别为0.029、0.026和0.023。综合均方根误差和空间相关系数的结果,可以认为从整体上来说陆面变量(参数)扰动对降水有较大影响。
|
图 5 均方根误差(a)和空间相关系数(b) Fig. 5 Area-averaged RMSE (a) and CORR (b) of 24-h accumulated precipitation |
图 6给出了SMO子集500、700和850 hPa 3个等压面上温度(T)、位势高度(Geopotential Height, GHT)、水汽混合比(Qvapor)及纬向风速(U)的逐时离散度(径向风速有类似结果)。由图 6可以看出在前3 h的预报中陆面变量SMO的初始扰动对3层大气的温、压、湿、风的影响较小,但是随着预报时间的增加,这种影响在逐渐增大。由图 6a可以看出500、700和850 hPa 3层大气温度场的第7小时预报的离散度可以达到0.01℃,之后随着预报时间的增加,其离散度有增加的趋势,到了第24小时预报,3层大气温度场的离散度可以达到0.045、0.045和0.036℃;由图 6b可以看出3层大气位势高度场的第6个小时预报的离散度可以到达1.50 gpm左右,第24小时预报的离散度可以达到7.22、5.12和7.46 gpm;由图 6c可以看出3层水汽混合比的第6小时预报的离散度可以达到1.50×10-5 g·kg-1以上,第24小时预报的离散度可以达到5.58×10-5、7.71×10-5和7.50×10-5 g·kg-1;由图 6d可以看出3层纬向风速的第7小时预报的离散度在0.15 m·s-1左右,第24小时预报的离散度达到0.87、0.57和0.47 m·s-1。总体上来说随着模拟时间的增加,预报的离散度有增加的趋势。由以上分析可以看出,陆面变量(参数)扰动不仅仅对低层大气有较大影响,甚至对高层500 hPa大气的温、压、湿、风也有较大影响,只是这种影响在预报的前几个时段较小,但是随着预报时间的增加,这种影响在逐渐显现出来,整体上来说在短期预报中陆面变量(参数)扰动对局地大气的环流形势的预报有较大影响。

|
图 6 逐时离散度的时间序列 (a)温度, (b)位势高度, (c)水汽混合比, (d)纬向风速 Fig. 6 Hourly divergence in 24 hours (a)temperature, (b)geopotential height, (c)qvapor, (d)zonal wind speed |
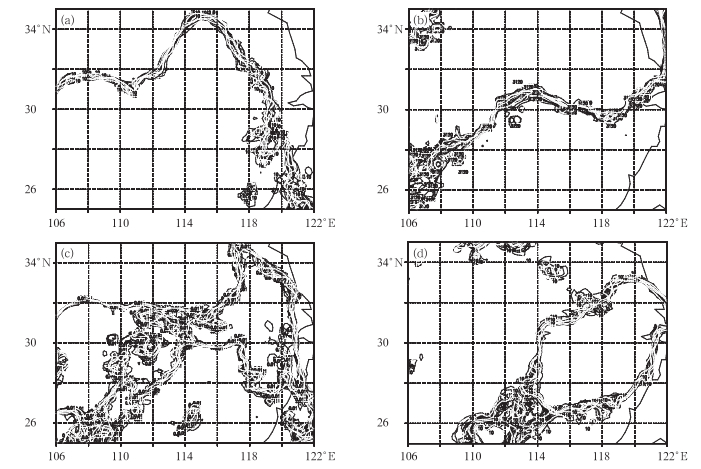
由各集合成员前3 h的温度场、位势高度场、水汽混合比场和风场的预报图(图略)可以看出各集合成员在前3个小时的预报中差异较小,之后各集合成员对温、压、湿、风预报的差异逐渐显现出来。图 7以700 hPa的6 h预报为例给出了SMO子集的30个集合成员的温度场、位势高度场、水汽混合比场和水平风速场的预报图。为了更清楚地看出集合成员之间的差异,这里以10℃温度场、3120 gpm位势高度场、0.01 g·kg-1水汽混合比场和10 m·s-1水平风速场为例给出,可以看出在6 h的预报中各集合成员的差异较为明显。这也是SMO子集各成员在6 h降水预报中有较为明显差异的主要原因。
|
图 7 集合成员6 h 700 hPa预报场 (a)10℃温度场, (b)3120 gpm位势高度场, (c)0.01 g·kg-1水汽混合比场, (d)10 m·s-1水平风速场 Fig. 7 6 h forecast at 700 hPa (a)the temperature of 10℃, (b)the geopotential height of 3120 gpm, (c)the qvapor of 0.01 g·kg-1, (d)the horizontal velocity of 10 m·s-1 |
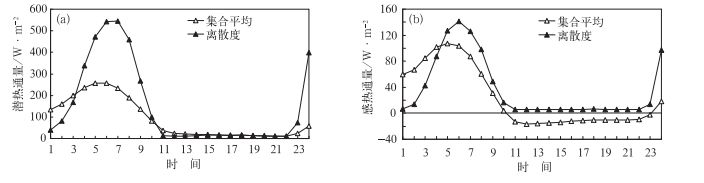
图 8给出了SMO子集潜热通量和感热通量的离散度及集合预报的区域平均值的时间变化序列。可以看出集合平均可以较好地预报出潜热通量和感热通量的日变化特征,在预报的第5~7小时(5月31日的中午13—15时)是潜热通量和感热通量的峰值区,中午时潜热通量和感热通量最大;之后潜热通量和感热通量逐渐减小,第10小时(5月31日晚上18时)以后潜热通量和感热通量较小,对应夜间的潜热通量和感热通量较小;到了预报的第23小时(6月1日早07时)以后潜热通量和感热通量的值开始增大。
|
图 8 潜热通量(a)及感热通量(b)的集合平均值及离散度的时间序列 Fig. 8 Hourly ensemble average and divergence in 24 h (a)latent heat flux, (b)sensible heat flux |
由潜热通量和感热通量的离散度(图 8a和8b)可以看出,在预报的第2小时各集合成员潜热通量和感热通量的差异已经较为明显,潜热通量的离散度为81.0 W·m-2,感热通量的离散度为13.9 W·m-2,之后随着预报时间的增加潜热通量和感热通量的离散度在增加,到了预报的第7小时潜热通量的离散度达到最大值544.9 W·m-2,到了预报的第6小时感热通量的离散度达到最大值141.6 W·m-2;之后潜热通量和感热通量的离散度逐渐减小,第10小时(5月31日晚上18时)以后潜热通量的离散度一直维持在10 W·m-2左右,感热通量的离散度一直维持5 W·m-2左右,整个夜间潜热通量和感热通量的离散度均较小,这主要是受夜间潜热通量和感热通量值较小的影响;天亮以后潜热通量和感热通量的值增大其离散度也迅速增大。
由地表通量的离散度的时间序列(图 8a、8b)和表征大气温、压、湿、风的大气温度、位势高度、水汽混合比、纬向风的离散度(图 6a、6b、6c和6d)的对比可以看出,陆面变量SMO初始值的改变引起地表通量和大气温、压、湿、风的改变并不是同步的,地表通量在预报的第2个小时即可有显著差异,而大气温、压、湿、风在预报的第6个小时有显著差异。从其影响机理上来说陆面变量SMO的改变会迅速引起地表潜热通量和感热通量的较大差异,而潜热通量和感热通量通过和大气的能量的交换导致局地大气温、压、湿、风的变化,从而对降水产生较大影响。
由水平衡的原理,陆面上某区域某时段内的降水主要可来自:该区域上方的水汽量;气柱中的云水量;气柱外围的辐合和区域表面蒸发。其中区域表面蒸发中转化为降水的部分与降水的比值为水汽的再循环比率。Trenberth(1998)认为对于500 km的典型陆地区域,水汽的再循环比率为5%~10%,全球陆面平均的水汽再循环比率为9%。本文中集合预报的平均表面水汽通量为3.62×10-5 kg·m-2·s-1,各集合成员平均表面水汽通量的最大差异(图略)为1.02×10-7 kg·m-2·s-1,集合成员间的差异较小。集合预报的24 h累积蒸发量为3.13 mm,各集合成员累积蒸发量的最大差异为0.01 mm,差异较小,而集合平均的24 h累积降水量为12.54 mm,24 h累积蒸发量的最大差异占24 h累积降水量的比例仅为0.08%,可以看出就算各成员的水汽蒸发量的差值全部转化为降水对降水的影响也较小,可以忽略不计,因此在陆面变量(参数)扰动中由于地表水汽垂直方向的湍流输送对降水的影响较小。
由以上分析可以看出陆面变量SMO初始值的改变带来地表通量的变化,地表通量通过陆气之间复杂的反馈过程会对大气的温、压、湿、风场产生影响,进而影响暴雨发生的区域和强度,相对而言扰动带来的地表水汽垂直方向的湍流输送对暴雨的影响要小得多。陆面变量TSL和陆面参数VEG的初始值的扰动也有类似结果,限于篇幅这里不一一讨论。
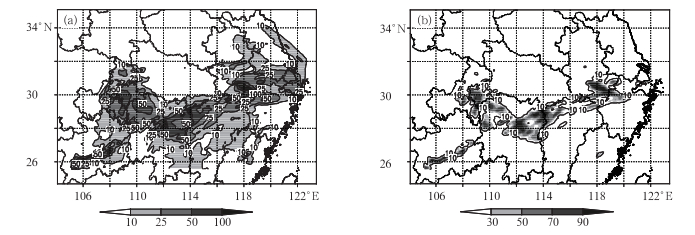
4 集合预报试验 4.1 概率预报试验图 9a以SMO子集为例给出了集合平均降水的空间分布,这里集合平均方法采用等权集合平均。由集合平均和控制试验的对比可以看出,集合平均的结果能更稳定地给出降水的空间分布,对29°N附近的三个强降水中心的体现较单一确定性的控制试验要好,更接近于实况,这在一定程度上说明了采用陆面变量(参数)扰动制作集合预报可以在一定程度上提高预报效果。
|
图 9 集合平均降水预报及大于50 mm降水概率预报 (a)SMO集合平均, (b)SMO子集降水概率 Fig. 9 Precipitation of averaged ensemble forecasts and the probability over 50 mm (a)average of SMO ensemble members, (b)the probability of SMO ensemble |
集合预报相对于单一确定性预报的优势就是可以用集合成员制作降水概率预报,图 9b以SMO子集为例给出了降水概率预报的结果,图中30、50、70、90分别表示降水概率为30%、50%、70%、90%。由降水概率图我们可以看出,实况降水量>50 mm量级的区域和各子集降水概率在30%以上的区域较为相似,在实际预报中必须对这一区域加以重视,同时可以看出各子集概率预报中降水概率在70%以上的区域和降水实况较为吻合,体现了降水概率预报对强降水预报的可信度较高。
4.2 集合预报检验表 1给出了集合平均和控制试验的24 h累积降水的ETS评分情况,可以看出对于0.1 mm以上降水,3个集合平均的ETS评分均小于控制预报的ETS评分,这主要是由于集合平均使降水虚假增多导致的。但是对于中雨、大雨和暴雨3个量级的降水,集合平均的ETS评分具有明显优势,并且随着降水量级的增大,集合平均ETS评分的优势增大。由3个子集集合预报的ETS评分和集合成员(图 4a、4b、4c和4d)的ETS评分的对比来看,3个子集集合预报的ETS评分在中雨、大雨、暴雨3个量级上均大于大多数集合成员,集合预报的结果比集合成员稳定可靠。
|
|
表 1 24 h累积降水ETS评分及集合预报相对于控制预报的改进情况 Table 1 ETS for 24-h accumulated precipitation and the improved of ensemble vs control |
为了定量评估集合预报与控制预报的效果,这里还参考柳崇健等(2002)的做法利用空间相关系数定义集合预报相对于控制预报的改进率为:
| $ R = \left( {{R_{\rm{e}}} - {R_{\rm{c}}}} \right)/{R_{\rm{c}}} \times 100\% $ | (7) |
式中,R为改进率,Re为集合预报的空间相关系数,Rc为控制预报的空间相关系数。
利用均方根误差定义集合预报相对于控制预报的改进率为:
| $ R = \left( {{\varphi _{\rm{c}}} - {\varphi _{\rm{e}}}} \right)/{\varphi _{\rm{c}}} \times 100\% $ | (8) |
式中,R为改进率,φe为集合预报的均方根误差,φc为控制预报的均方根误差。
由表 2和表 3可以看出,从24 h累积降水的均方根误差和空间相关系数上来看,集合预报的结果优于控制预报,利用陆面变量(参数)扰动制作集合预报可以提高预报效果。同时由集合预报的均方根误差、空间相关系数和集合成员(图 5a和5b)进行对比可以看出,3个集合预报的均方根误差均小于大多数集合成员,空间相关系数均大于大多数集合成员,集合平均的结果比集合成员稳定可靠。总体上说集合预报的结果具有明显优势,利用陆面变量(参数)扰动制作集合预报可以改善预报效果。
|
|
表 2 24 h累积降水均方根误差及集合平均相对于控制预报的改进率 Table 2 RMSE of 24-h accumulated precipitation and the improved rate of ensemble vs control |
|
|
表 3 24 h累积降水空间相关系数及集合预报相对于控制预报的改进率 Table 3 CORR of 24-h accumulated precipitation and the improved rate of ensemble vs control |
本文利用中尺度模式WRF3.2.1,通过对陆面变量SMO(土壤湿度)、TSL(土壤温度)和陆面参数VEG(植被覆盖率)进行初始场的随机扰动,探讨暴雨预报对陆面变量(参数)扰动的敏感性,并进行集合预报试验,得到以下主要结论:
(1) 从降水特征量和评估参数结果来看,此次暴雨过程对不同陆面变量(参数)扰动表现出了不同的敏感性,总体上来讲暴雨过程对陆面变量(参数)扰动是敏感的。
(2) 从影响降水的时间尺度上来看,SMO子集在模拟的第5小时,即可对降水有显著影响,VEG子集、TSL子集在模拟的第7小时也可对降水有显著影响,这说明陆面变量(参数)扰动影响降水的时间尺度在10 h以内,甚至可以小于6 h。
(3) 从降水落区范围和ETS评分的结果来看,陆面变量(参数)扰动对各量级降水都有一定影响,但是对大量级降水的影响要大于对小量级降水的影响。这说明利用陆面变量(参数)扰动构造集合成员,集合成员间存在一定的不确定性,且对于大量级降水,各集合成员间的不确定性更大,这也反映了模式对大量级降水的预报较差,在单一、确定性预报中模式对大量级降水的预报结果可信性较小。
(4) 从影响机理上来看,陆面变量(参数)初始值的改变带来了地表通量的变化,地表通量通过陆气之间复杂的反馈过程会对大气的温、压、湿、风产生影响,进而影响暴雨发生的区域和强度,相对而言扰动带来的地表水汽垂直方向的湍流输送对暴雨的影响要小得多。
(5) 从集合预报的效果来看,不论是ETS评分还是均方根误差和空间相关系数,集合预报的结果均要好于控制预报的结果;从集合平均和集合成员的对比可以看出集合平均比集合成员稳定可靠;由降水概率预报可以看出,降水概率预报可以提供一些有用的信息,尤其对强降水的预报有一定的指示意义。
(6) 试验结果表明,采用陆面变量(参数)扰动来构造集合预报是可行的,在初值集合预报中,引进这些参数或变量作为集合成员是十分有意义的。本文结果为初值集合预报的改进提供了一种新方法,对提高暴雨数值预报的水平具有重要的现实意义。
陈静, 薛纪善, 颜宏, 2005. 一种新型的中尺度暴雨集合预报初值扰动方法研究[J]. 大气科学, 29(5): 717-726. |
杜钧, 陈静, 2010. 单一值预报向概率预报转变的基础:谈谈集合预报及其带来的变革[J]. 气象, 36(11): 1-11. DOI:10.7519/j.issn.1000-0526.2010.11.001 |
韩焱红, 矫梅燕, 陈静, 等, 2013. 基于贝叶斯理论的集合降水概率预报方法研究[J]. 气象, 39(1): 1-10. DOI:10.7522/j.issn.1000-0534.2012.00001 |
纪永明, 陈静, 矫梅燕, 等, 2011. 基于多中心TIGGE资料的区域GRAPES集合预报初步试验[J]. 气象, 37(4): 392-402. DOI:10.7519/j.issn.1000-0526.2011.04.002 |
柳崇健, 刘英, 康红文, 2002. 一种新的物理耗散技术及其在中尺度数值天气预报模式中的应用[J]. 中国科学D辑, 32(3): 255-264. |
刘家俊, 张立凤, 关吉平, 等, 2010. 集合预报产品在台风麦莎预报中的应用[J]. 气象, 36(5): 21-31. DOI:10.7519/j.issn.1000-0526.2010.05.003 |
牛震宇, 张立凤, 2006. 基于集合预报思想对一次暴雨过程的数值模拟[J]. 解放军理工大学学报, 7(1): 73-79. |
任志杰, 陈静, 田华, 2011. T213全球集合预报系统物理过程随机扰动方法研究[J]. 气象, 37(9): 1049-1059. DOI:10.7519/j.issn.1000-0526.2011.09.001 |
谭燕, 陈德辉, 2008. 河南"75.8"大暴雨的中尺度集合预报试验[J]. 气象, 34(9): 10-20. DOI:10.7519/j.issn.1000-0526.2008.09.002 |
田伟红, 庄世宇, 2008. ETKF方法在区域集合预报中的初步应用[J]. 气象, 34(8): 35-39. DOI:10.7519/j.issn.1000-0526.2008.08.005 |
王雨, 闫之辉, 2007. 降水检验方案变化对降水检验评估效果的影响分析[J]. 气象, 33(12): 53-61. DOI:10.7519/j.issn.1000-0526.2007.12.008 |
夏凡, 陈静, 2012. 基于T213集合预报的极端天气预报指数及湿度预报应用试验[J]. 气象, 38(12): 1492-1501. |
郑峰, 2008. 集合预报初值扰动在天气预报中的应用研究进展[J]. 科技导报, 26(19): 90-95. DOI:10.3321/j.issn:1000-7857.2008.19.018 |
张朝林, 苗世光, 李青春, 等, 2007. 北京精细下垫面信息引入对暴雨模拟的影响[J]. 地球物理学报, 50(5): 1373-1382. |
曾新民, 吴志皇, 宋帅, 等, 2012. WRF模式不同陆面方案对一次暴雨事件模拟的影响[J]. 地球物理学报, 55(1): 16-28. |
曾新民, 张强, 2009. 一次暴雨天气对陆面参数扰动的敏感性数值影响[J]. 解放军理工大学学报, 10(4): 384-390. |
Bishop C H, Ethern B J, Majumdar S, 2001. Adaptive sampling with the ensemble transform Kalman filter. PartⅠ: theoretical aspects[J]. Mon Wea Rev, 129(3): 420-436. DOI:10.1175/1520-0493(2001)129<0420:ASWTET>2.0.CO;2 |
Brooks H E, Cortinas J V, Janish P R, et al. 1996. Application of short-range numerical ensembles to forecasting of hazardous winter weather. 11th Conference on Numerical Weather Predication. Norfolk; Amer Meteor Soc, 70-71.
|
Buizza R, Miller M, Palmer T N, 1999. Stochastic representation of model uncertainties in the ECMWF ensemble prediction system[J]. Quart Roy Meteor Soc, 125: 2887-2908. DOI:10.1002/qj.49712556006 |
Buizza R, Palmer T N, 1995. The singular vector structure of the atmosphere global circulation[J]. Atmos Sci, 52(9): 1434-1456. DOI:10.1175/1520-0469(1995)052<1434:TSVSOT>2.0.CO;2 |
Buizza R, Palmer T N, 1998. Impact of ensemble size on ensemble prediction[J]. Mon Wea Rev, 126(9): 2503-2518. DOI:10.1175/1520-0493(1998)126<2503:IOESOE>2.0.CO;2 |
Du J, Mullen S L, Sanders F, 1997. Short-range ensemble forecasting of quantitative precipitation[J]. Mon Wea Rev, 125(10): 2427-2459. DOI:10.1175/1520-0493(1997)125<2427:SREFOQ>2.0.CO;2 |
Hamill T M, Colucci S J, 1997. Verification of Eta-RSM short-range ensemble forecasts[J]. Mon Wea Rev, 125(6): 1312-1327. DOI:10.1175/1520-0493(1997)125<1312:VOERSR>2.0.CO;2 |
Hoffman R N, Kalnay E, 1983. Lagged average forecasting, an alternative to Monte Carlo forecasting[J]. Tellus, 35A: 100-118. DOI:10.1111/tela.1983.35A.issue-2 |
Houtekamer P L, Derome J, 1995. Methods for ensemble prediction[J]. Mon Wea Rev, 123(7): 2181-2196. DOI:10.1175/1520-0493(1995)123<2181:MFEP>2.0.CO;2 |
Leith C E, 1974. Theoretical skill of Monte Carlo forecasts[J]. Mon Wea Rev, 102(6): 409-418. DOI:10.1175/1520-0493(1974)102<0409:TSOMCF>2.0.CO;2 |
Lorenz E N, 1963. Deterministic nonperiodic flow[J]. Atmos Sci, 20(2): 130-141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 |
Lorenz E N, 1965. A study of the predictability of 28-variable atmospheric model[J]. Tellus, 17(3): 321-333. DOI:10.3402/tellusa.v17i3.9076 |
Majumdar S, Bishop C H, Ethern B J, 2002. Adaptive sampling with the ensemble transform Kalman filter. PartⅡ: Field Program implementation[J]. Mon Wea Rev, 130(5): 1356-1369. DOI:10.1175/1520-0493(2002)130<1356:ASWTET>2.0.CO;2 |
Pielke R A, 2001. Influence of the spatial distribution of vegetation and soils on the prediction of cumulus convective rainfall[J]. Rev Geophys, 39: 151-177. DOI:10.1029/1999RG000072 |
Toth Z, Kalnay E, 1993. Ensemble forecasting at NMC: The generation of perturbation[J]. Bul Amer Meteor Soc, 74(12): 2317-2330. DOI:10.1175/1520-0477(1993)074<2317:EFANTG>2.0.CO;2 |
Toth Z, Kalnay E, 1997. Ensemble forecasting at NCEP and the Breeding method[J]. Mon Wea Rev, 125(12): 3297-3319. DOI:10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2 |
Trenberth K E, 1998. Atmospheric moisture residence times and cycling: Implications for rainfall rates with climate change[J]. Climate Change, 39(4): 667-694. DOI:10.1023/A:1005319109110 |
Tryhorn L, Gallucci J, Lynch A, et al, 2008. On the meteorological mechanisms driving postfire flash floods: A case study[J]. Mon Wea Rev, 136(5): 1778-1791. DOI:10.1175/2007MWR2218.1 |
Wang X, Bishop C H, 2003. A comparison between ETKF and breeding ensemble forecast scheme[J]. Atmos Sci, 60(5): 1140-1158. |
 2014, Vol. 40
2014, Vol. 40 