2. 中国气象科学研究院灾害天气国家重点实验室,北京 100081;
3. 南京信息工程大学气象灾害预报预警与评估协同创新中心,南京 210044;
4. 中国船舶重工集团第七二四研究所,南京 210003
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081;
3. Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science and Technology, Nanjing 210044;
4. No.724 Research Institute of CSIC, Nanjing 210003
中尺度对流系统(mesoscale convective systems, MCSs)是造成暴雨、雷达大风和冰雹等灾害天气的重要系统,而线状对流所产生的雷暴大风天气更容易导致多点并发的致灾情况。如2004年7月12日,从江苏溧阳一带发展起来的雷暴云在上海发展成为飑线,上海遭受7~11级雷雨大风,闵行出现了龙卷风,造成多处房屋倒塌和人员伤亡(刘淑媛等,2007)。2009年6月3日,一次罕见的强天气袭击黄淮地区,在安徽发展成为飑线,造成严重的人员伤亡和经济损失(孙虎林等,2011),多个地面自动站瞬时大风超过20 m·s-1。2011年4月17日,一次线状中尺度对流系统从广西进入广东,造成广州、佛山和肇庆等地出现强冰雹、雷达大风等强对流天气,期间云浮都杨镇杨柳站记录到全省最大阵风44.3 m·s-1(郭媚媚等,2012)。
国内外学者从几十年前就开展线状中尺度对流系统的研究。丁一汇等(1982)收集我国18个飑线个例,把它们分类为槽后型、槽前型、高后型和台风倒槽型4类,研究不同类型飑线的天气背景、触发条件和物理条件,最后与暴雨的物理条件做了对比分析,发现不同类型飑线天气条件和物理条件有明显差别,飑线与暴雨的物理条件也存在明显差别,主要差异体现在飑线对应中、上层干冷空气,水汽辐合小,抬升指数大,自由对流高度高。随着观测工具的进步,高时空分辨率的雷达等资料被应用到飑线过程的分析中来。刘黎平等(2007)利用双偏振雷达观测资料,用β方法和约束条件下的Λ反演方法,分析了飑线过程降水粒子相态、雨滴谱分布和相态混合区融化过程,结合四维变分方法反演风场,研究了飑线过程中雨滴谱与风场结构的关系。庄薇等(2010)利用双多普勒雷达同步观测资料、地面自动站资料、探空资料、NECP再分析场资料和双多普勒雷达风场反演资料,分析新疆一次强飑线过程,发现了中低层风场辐合是造成此次飑线的主要原因。孙虎林等(2011)利用雷达拼图资料、自动站资料、地闪资料和四维变分反演风场资料,分析了黄淮地区一次强飑线成熟阶段特征。在收集了多年雷达资料的基础上,线状中尺度对流系统的普查研究在雷达拼图资料上得到开展。Geerts(1998)利用一年的雷达拼图资料统计分析美国中尺度对流系统,其中线性中尺度对流系统占47%。Parker等(2000)利用1996年5月和1997年5月的雷达拼图资料研究了美国线性中尺度对流系统的统计特征。王晓芳等(2012)利用区域雷达拼图和各种观测资料统计长江中下游地区MCSs活动特征,重点分析线状MCSs的分类、持续时间、地理分布、日变化特征和环境场特征(王晓芳等,2012;王晓芳,2012)。Meng等(2013)利用2008和2009年的雷达拼图资料普查了中国东部的飑线特征。
基于雷达资料的短临预报和自动识别是非常重要的研究工作,目前已发展了多种算法,如TREC(Tracking Radar Echoes by Correlation)(Rinehart et al, 1979)、阵风锋自动识别算法(Diana,1987)、雷暴识别跟踪分析预报算法(Thunder storm Identification, Tracking, Analysis and Nowcasting,TITAN)(Dixon et al,1993)、风暴单体识别追踪算法(Storm Cell Identification and Tracking Algorithm,SCIT)(Johnson et al,1998)、火情自动识别系统(黄克慧等,2011)、暴雨云团的识别方法(Lakshmanan et al,2003; 王改利等,2007;杨吉等,2012)、0℃层亮带的识别方法(庄薇等,2013)和冰雹预报预警方法(段鹤等,2014)等。其中TREC、TITAN和SCIT更是各个短临预报系统的重要组成部分,如中国的SWAN,香港的小涡旋(Li et al,2000),美国的ANC(Auto-Nowcast System)(Mueller et al, 2003)。这些算法对业务工作和科学研究都提供了极大的帮助。但目前还没有查阅到一个能够实现线状MCSs自动识别的相关算法。
因此,有必要开展线状MCSs的自动识别方法研究,这是一项很有意义的工作。本文拟在MCSs自动识别、跟踪(杨吉等,2012)的基础上,采用动态模板函数法判断MCSs线性程度,实现线状MCSs的自动识别。并以我国多个对流天气过程对该方法进行检验。
1 资料原始雷达资料由我国气象部门的新一代天气雷达网提供。使用中国气象科学研究院灾害天气国家重点实验室开发的多普勒天气雷达三维数字组网系统把原始雷达资料转化成雷达拼图资料。该系统首先将不同型号、不同波段雷达的体扫数据转换为统一格式,对统一格式的数据进行质量控制,再采用径向与方位上的最近邻居法和垂直线性内插法将单站雷达数据从极坐标系转换到经纬度和垂直高度坐标系,然后采用指数权重法将各单站的格点数据拼到一个大范围的经纬度和垂直高度坐标系中。得到水平分辨率为0.01°×0.01°,时间分辨率为6 min的组合反射率数据。
选取以下4次3种不同类型的天气过程,检验、分析算法在不同天气过程中的表现。4次天气过程分别为:2011年6月23日,一次线状MCSs袭击了北京及周边地区,强降水造成城市多处被淹没(郑祚芳等,2013),此次使用了北京S、天津和承德雷达站基数据进行组网。2012年5月16日,一次线状MCSs横扫苏北,造成冰雹大风和强降水天气(张涛等,2013),这次使用盐城、连云港、徐州和南京雷达站基数据进行组网。2009年6月3—4日,一次强飑线天气过程袭击了我国的黄淮地区(郑媛媛等,2011),飑线呈“厂”字型,此次天气影响范围大,使用了郑州、商丘、濮阳、三门峡、驻马店、徐州和合肥7部雷达站的基数据进行组网。2011年7月29日,一次中尺度对流系统造成的强降水袭击北京,城市多处积水,多个航班延误或取消,此次使用北京S、天津和承德雷达站基数据进行组网。
2 方法在以往的研究中,已出现雷达资料上对线状MCSs的定义,如表 1,他们对不同地区的线状MCSs做了类似的定义。参考这些研究并根据我国实际情况,本文认为满足以下两个条件为线状MCSs:(1) 由层云(15 dBz)连接的对流云(40 dBz)组成的系统长轴大于100 km,持续时间超过4 h;(2) 这个系统长宽比大于5:1,持续时间超过2 h。
|
|
表 1 线状中尺度对流系统定义 Table 1 Criteria used to define linear MCSs |
根据对线状MCSs的定义,算法采用MCSs自动识别法识别出由层云(15 dBz)连接的对流云(40 dBz)系统,这个系统长轴如果大于100 km,则计算相关参数,采用动态模板函数法计算得分值结果,并通过MCSs跟踪法进行跟踪,如果得分值结果≥1.2持续时间超过2 h,系统长轴≥100 km持续时间超过4 h,则认为这个系统是线状MCSs。杨吉等(2012)对MCSs自动识别和跟踪做了详细的描述,方法如下。
首先在组合反射率因子上进行一个卷积过程,使资料变得光滑。卷积过程使用的卷积函数为:
| $ C\left({x, y} \right) = \sum {\phi \left({u, v} \right)} f\left({x - u} \right)\left({y - u} \right)\ $ | (1) |
式中,f是资料场,
| $ \left\{ {_{\phi \left({x, y} \right) = 0, {\rm{if}}\left({{x^2} + {y^2} > {R^2}} \right)}^{\phi \left({x, y} \right) = H, {\rm{if}}\left({{x^2} + {y^2} \le {R^2}} \right)}} \right.\ $ | (2) |
参数R和H不相互独立,其关系如下:
| $ \pi {R^2}H = 1\ $ | (3) |
式中,卷积过程中影响半径R是唯一可改变的参数。一旦R被选定,H由式(2) 决定。本文中采用的是4个格距。
在得到的卷积场中,识别出层云(15 dBz)和对流云(40 dBz),将落在同一个层云范围内的对流云归为一个系统,这样的系统满足长轴>100 km,持续时间超过4 h,则被认为是中尺度对流系统。在识别的过程中,相关参数被记录下来。
采用适用于中尺度对流系统的最小价值函数法匹配前后时刻的系统,排除错误匹配后实现跟踪。
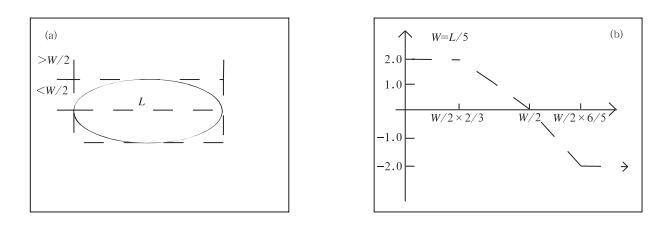
动态模板函数法介绍如下:中尺度对流系统一般为不规则多边形,形状复杂,先勾勒出中尺度对流系统的多边形,然后再用椭圆去拟合这个多边形,根据拟合椭圆得到拟合椭圆长轴及所在直线。过MCSs内部对流云点,与拟合椭圆长轴所在直线垂直的最远两直线间距离,作为中尺度对流系统的长轴L,也是动态模板的长。在本文对线状MCSs的定义中,其中一个条件是长宽比大于5:1,如果这个中尺度对流系统是线状的,则它的宽最大应为MCSs长轴的1/5,设定动态模板的宽是MCSs系统长轴的1/5。如图 1a,椭圆代表自动识别得到的MCSs,虚线所组成的图形代表动态模板,MCSs长轴L为动态模板长轴,W=L/5。不同MCSs计算得到不同L和W。
|
图 1 (a)动态模板,(b)得分函数 Fig. 1 (a) Dynamic templet, (b) score function |
图 1b中得分函数横坐标为MCSs内部对流云回波点到拟合椭圆长轴的几何距离,纵坐标为得分值。若MCSs长轴直线为ax+by+c=0,点的坐标为(x0, y0)。几何距离由以下公式得到:
| $ d = |\frac{{a{x^0} + b{y^0} + c}}{{\sqrt {{a^2} + {b^2}} }}|\ $ | (4) |
当对流云回波点到长轴的几何距离小于W/2×2/3时,对流云距离长轴较近,给回波点一个较高的得分值2.0,当距离在超过W/2×2/3,小于W/2时,得分值有一个缓慢下降的过程,当距离超过W/2,即在长宽比为5:1的长方形范围之外,得分值随距离增加从0迅速下降至-2.0。
在识别过程中,每一个满足MCSs空间条件的系统,使其内部对流云都经过以上计算,累加所有对流云回波点的得分值,比上系统内部对流云面积(对流云回波点数累加)得到得分值结果。该得分值在-2.0~2.0,如果得分值持续超过2 h>1.2,则认为其满足线状MCSs定义第二个条件。同时满足线状MCSs定义第一个条件,则认为其为线状MCSs。
被识别为线状MCSs后,输出其各种参数。如各个时刻得分值、面积、长轴方向、长轴、线状MCSs中心位置、移动速度和移动方向等。
面积:每一个格点的面积是1 km2,将同一个线状MCSs的所有对流云格点累加起来便得到面积。
长轴朝向:上文中拟合椭圆长轴所在直线与正东方向的夹角,单位为°,以x轴正方向为0°,逆时针旋转为正。
长轴:过线状MCSs内部对流云点,与拟合椭圆长轴所在直线垂直最远两直线间的距离,作为线状MCSs的长轴,单位为km。
中心位置以回波值为权重得到, ε(x, y)为(x, y)点的回波值。
| $ x = \frac{{\sum {x \in \left({x, y} \right)} }}{{\sum { \in \left({x, y} \right)} }}, y = \frac{{\sum {y \in \left({x, y} \right)} }}{{\sum { \in \left({x, y} \right)} }}\ $ | (5) |
移动速度和移动方向由前后时刻线状MCSs中心位置计算得到。
该算法经过特殊个例的测试,如电磁干扰以及存在地物回波的资料进行测试,结果表明电磁干扰以及地物回波不会被误识别为线状MCSs。下文给出具体实例说明。
3 结果分析与讨论采用上文方法对4次3种不同类型天气过程资料进行处理,算法在个别时刻存在跟踪“遗漏”情况发生,人工校准后提取出完整天气过程的多个参数和算法得分值,得到结果及相关分析如下。
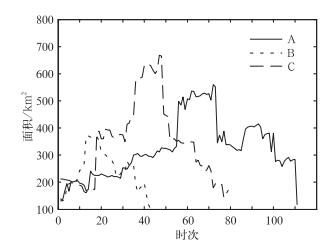
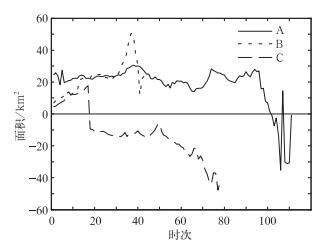
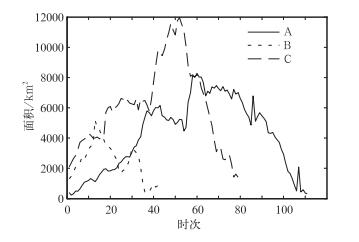
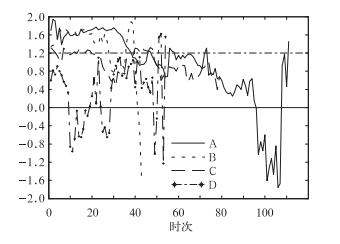
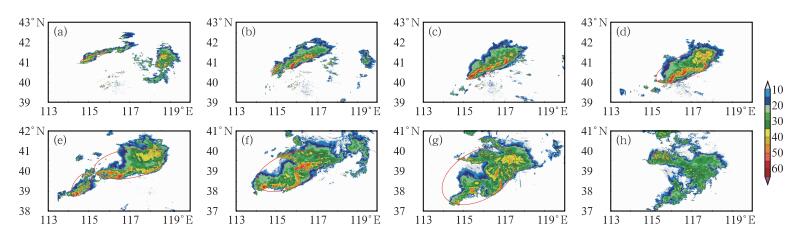
北京2011年6月23日发生一次线状MCSs过程,图 2~图 5中,曲线A代表此次过程的参数随时间变化。03:06(世界时,下同)对流初生,此时还不具备线状MCSs的空间尺度和形态。对流迅速发展,图 6a(03:30)中对流排列成线状,系统呈西南—东北朝向,长轴尺度已超过100 km,算法得分值为1.69,该系统已被算法识别并记录相关参数信息。对流继续发展,前进方向右侧不断有新单体生成、加入到系统中来,图 2和图 3中面积与长轴不断增加,图 4中长轴朝向比较稳定,对流一直保持良好的线性状态向东南方向移动(图 6b),算法得分值保持在1.30以上直到07:12(35时次之前),系统已满足线状MCSs定义第二个条件保持2 h长宽比大于5:1,系统的空间尺度具备一定规模,强度近60 dBz,且在继续增强。在此期间,得分值的小幅波动主要由系统内对流生成造成。对流生成同时影响着系统长轴的长度或倾斜角度,导致得分值的变化。07:12以后,系统前进方向左后侧回波开始发展(图 6d),图 2和图 3中面积与长轴仍然不断增加,图 4中长轴方向开始缓慢调整,算法得分值逐渐下降。09:12(55时次)下降至0.69,该系统西南方向发展出一个较小的系统(图 6e),即将与之发生合并。09:18西南侧系统与系统本身合并,增强了系统的线性状态,图 2和图 3中面积与长轴同时出现了“跳跃”上升的变化,图 4中无明显变化,图 5中的算法得分值上升至1.31。到11:48(81时次),得分值下降至0.45(图 6f)。自35—81时次,得分值保持在1.44~0.45,得分值的缓慢变化是由于回波发展演变,小幅度波动主要由对流生成与其他系统合并造成,此外,部分对流的消亡也是原因之一。81时次之后(图 6g),系统前进方向左侧回波逐渐消亡,右侧维持,系统强度开始减弱,强对流单体逐渐消失,回波梯度、长轴和面积减小,图 4中长轴朝向开始大幅度波动,回波形态呈非规则状,得分值下降,甚至出现负值。14:48,回波已不满足空间尺度条件,系统消亡。在此期间的得分值变化剧烈,主要由于回波消亡造成,回波的消亡引起系统长轴的长度或倾斜角度大幅度变化,从而影响得分值。此次线状MCSs过程被算法正确识别到,识别从03:30开始直到14:48结束,持续9 h 18 min,过程中有3 h 42 min保持良好的线性状态(如图 6a~6c),算法得分值随时间的缓慢变化和“跳跃”都能够从雷达回波实际演变情况与参数变化中得到解释,得分值能够反映此次天气过程的线性状态,取得较好的效果。
|
图 2 系统面积随时间变化 (A为2011年6月23日,B为2012年5月16日,C为2009年6月3日) Fig. 2 The change of area with time (A indicates 23 June 2011, B indicates 16 May 2012, C indicates 3 June 2009) |
|
图 5 算法得分值随时间变化 (说明同图 2,D为2011年7月29日) Fig. 5 The change of algorithm score with time (Same as Fig. 2, D in dicates 29 July 2011) |
|
图 6 2011年6月23日北京线状MCSs(世界时) (a)03:30, (b)05:30, (c)06:30, (d)07:30, (e)09:12, (f)11:48, (g)13:18, (h)14:48 Fig. 6 The linear MCSs in Beijing on 23 June 2011 (UTC) (a) 03:30, (b) 05:30, (c) 06:30, (d) 07:30, (e) 09:12, (f) 11:48, (g) 13:18, (h) 14:48 |
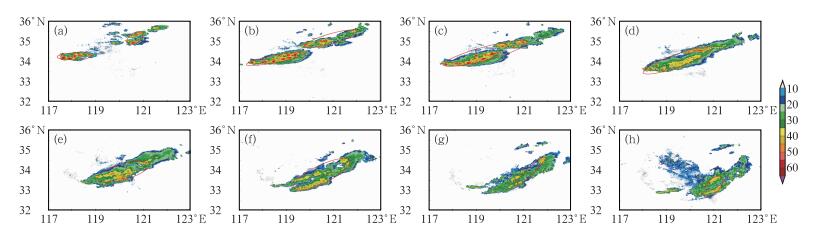
2012年5月16日江苏发生一次线状MCSs过程,图 2~图 5中,曲线B代表此次过程参数随时间的变化。06:54对流初生,07:12(图 7a)发展为线状,长轴近似于东西朝向,向东南方向移动,回波强度已达55 dBz以上,图 5中曲线B得分值为1.34。系统继续发展,图 2和图 3中面积增大,长轴加长,其前进方向右侧不断有对流生成加入到系统,左侧发展出一个对流系统(图 7b)。在08:30 (图 7c)时发生合并,合并前后都保持着良好的线性状态,图 2和图 3中曲线B在12:00—13:00刻出现了明显的“跳跃”,图 4中曲线B长轴朝向有一个轻小幅度调整,在图 5中曲线B并无明显的得分值“跳跃”现象,参数变化与实际情况对应较好。直到09:18(27时次),回波线性状态良好,得分值一直保持在1.25以上,此时已满足线状MCSs定义的第二个条件(图 7d)。09:18以后,系统前进方向右后方发展出一条弱回波带,左侧回波强度明显减弱,系统短轴得到加长,图 4中长轴朝向开始出现调整,导致图 5中曲线B得分值下降。10:30(34时次)之后,系统进入消亡期,回波强度进一步下降,面积、长轴和长轴朝向同时出现调整,得分值开始大幅度波动(图 7f)。12:00系统消亡。算法正确识别到此次线状MCSs过程,识别从07:12开始直到12:00结束,持续4 h 48 min,期间有2 h 48 min保持良好线性状态(如图 7a~7d),算法得分值与参数变化合理地对应了雷达回波实际情况,较好地反映了此次天气过程中线性状态的变化。
|
图 7 2012年5月16日江苏线状MCSs(世界时) (a)07:12, (b)08:12, (c)08:30, (d)09:18, (e)10:00, (f)10:30, (g)11:00, (h)11:30 Fig. 7 The linear MCSs in Jiangsu on 16 May 2012 (UTC) (a) 07:12, (b) 08:12, (c) 08:30, (d) 09:18, (e) 10:00, (f) 10:30, (g) 11:00, (h) 11:30 |
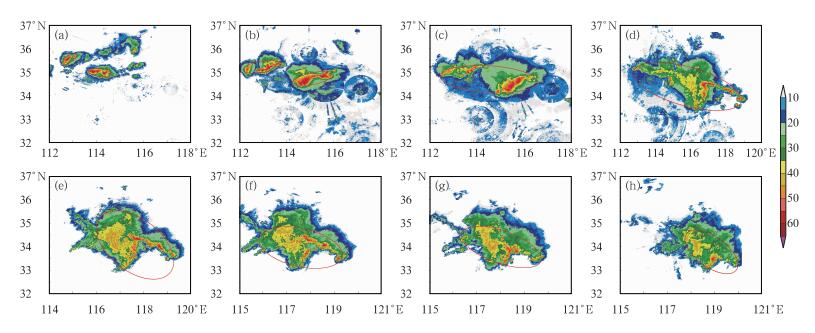
2009年6月3日黄淮地区发生一次强飑线天气过程,图 2~图 5中,曲线C代表此次飑线过程的参数随时间变化。10:12对流初生,于11:00(图 8a)发展到长轴超过100 km,但是并不具有较好的线性形态,西北方向同样发展出一个较强的对流。回波发展,强度增强。到12:00(图 8b)回波已达65 dBz,回波长轴已近200 km。13:00(图 8c)系统与西北方向的对流发生合并,在初生到此期间,没有保持较好的线性状态,图 5中对应时间段(21时次之前)曲线C在1.2附近波动。15:00(图 8d)系统中出现了“厂”字型飑线,由西北—东南朝向和西南—东北朝向的两条回波带组成,此刻西北方向还有一条相对较弱的回波带,使得系统长轴较长,得分值趋近1.2。16:00(图 8e)西北方向的回波带消亡,得分值迅速下降到0.8附近(49时次),并在0.8附近维持小幅度波动较长时间,相应时间段回波无迅速变化或合并分裂发生,与得分值对应情况较好。17:00,回波强度开始减弱,回波梯度和面积减小,回波开始进入消亡期(图 8g)。19:00,系统已不满足MCSs空间尺度条件。进入消亡期后,对应时间段得分值出现多次大幅波动,出现波动的时刻,对应了系统由于消亡造成的回波形态明显变化。这种现象表明了算法对回波变化有迅速的判断能力。此次天气过程中,“厂”字型飑线没有被算法识别为线状MCSs,得到结果符合算法的设计原理,相应表明算法不适用于其他类型的飑线识别。
|
图 8 2009年6月3日黄淮飑线(世界时) (a)11:00, (b)12:00, (c)13:00, (d)15:00, (e)16:00, (f)16:30, (g)17:00, (h)18:00 Fig. 8 The squall line in Huanghuai on 3 June 2009 (UTC) (a) 11:00, (b) 12:00, (c) 12:30, (d) 13:00, (e) 15:00, (f) 16:00, (g) 16:30, (h) 17:30 |
从图 2与图 3来看,得到的面积与长轴参数随时间变化能够看出系统的发展、成熟和消亡过程。由于系统发生分裂与合并导致面积(图 2)的突变,在相应长轴(图 3)中有较好的对应,面积、长轴长度及长轴朝向(图 4)与雷达回波实际情况对应较好,说明算法得到参数结果正确。
2011年7月29日发生一次MCSs天气过程(图 9)。7月29日00:00之前,40°N、116°E附近对流初生,00:00 MCSs长轴超过100 km,图 5中曲线D得分值为0.6,回波呈非规则状,向东偏北方向移动。MCSs北面不断生成对流,并加入到系统中来,使得得分值经过短暂波动后不断下降,01:30 MCSs回波结构呈类似“S”形状,得分值已为负。此时,系统南面对流开始消亡,北面前进方向对流不断新生,导致回波形态不断变化,图 5中曲线D上升后再次下降为负值。之后MCSs南北对流逐渐分裂开来,得分值上升为正值后小幅波动。04:00以后,MCSs回波强度开始减弱,面积减小,进入消亡期,得分值开始出现大幅度波动,原因及得分值波动情况与上文几次天气过程后期情况较为相似。此次过程回波形态基本无线性状态出现,得分值反映情况与实况一致,少有1.0以上得分情况出现,算法得分值结果能够较好反映此次天气过程的非线性状态。
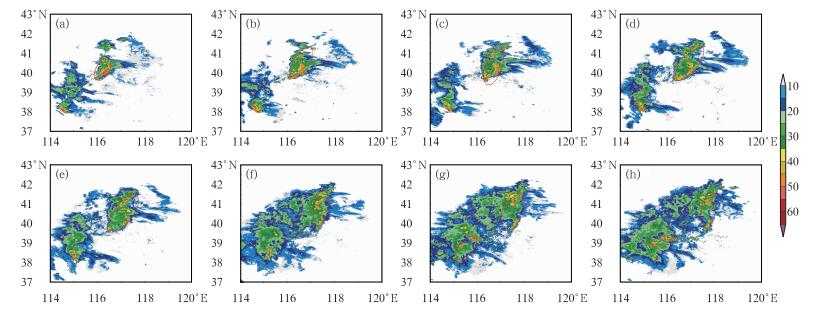
|
图 9 2011年7月29日北京MCSs过程(世界时) (a)00:00, (b)00:30, (c)01:00, (d)01:30, (e)02:00, (f)02:30, (g)03:00, (h)03:30 Fig. 9 The MCSs in Beijing on 29 July 2009 (UTC) (a) 00:00, (b) 00:30, (c) 01:00, (d) 01:30, (e) 02:00, (f) 02:30, (g) 03:00, (h) 03:30 |
图 5中A和B为两次线状MCSs天气过程得分值曲线,C为“厂”字型飑线天气过程得分值曲线,曲线D为团状对流系统得分值曲线。从图 5中可以看出,曲线A和B在系统呈现较好线性状态时期得分值明显高于系统非线性状态时期。曲线A和B在系统呈现较好线性状态时期得分值也明显高于“厂”字型飑线和MCSs天气过程。说明算法对中尺度对流系统线性状态有较好的判断能力。当系统发生分裂、合并、对流初生和消亡时,导致回波形态发生变化,算法得分值能够很好反映系统的线性状态变化。得分值在系统消亡时期,由于回波形态变化较大,往往会发生较大幅度波动。
4 结论本文在MCSs自动识别方法的基础上,提出了基于动态模板函数的线状MCSs自动识别方法,并用两次线状MCSs天气过程,一次“厂”字型飑线天气过程和一次MCSs天气过程对算法实施检验,结合算法提取到的系统面积、系统长轴和长轴朝向参数进行分析,得到以下结果:
(1) 算法能够实现对线状MCSs天气过程的自动识别。算法得分值结果能够较好反映线状MCSs各个阶段线性状态,能够反映线状MCSs和非线状飑线及MCSs天气过程的差异。对系统由于分裂与合并造成的回波形态“突变”,从得分值结果上能够得到较好的反映。
(2) 算法能够实现对线状MCSs天气的跟踪、一般情况下跟踪效果较好,在分裂或者合并的时刻存在跟踪不到的情况发生,这是由于分裂或者合并造成的系统重心位置位移过大造成。
(3) 算法得到的参数正确有效,能够反映实际情况。
丁一汇, 李鸿洲, 章名立, 等, 1982. 我国飑线发生条件的研究[J]. 大气科学, 6(1): 18-27. |
段鹤, 严华生, 马学文, 等, 2014. 滇南冰雹的预报预警方法研究[J]. 气象, 40(2): 174-185. DOI:10.7519/j.issn.1000-0526.2014.02.005 |
郭媚媚, 赖天文, 罗炽坤, 等, 2012. 2011年4月17日广东强冰雹天气过程的成因及特征分析[J]. 热带气象学报, 28(3): 425-432. |
黄克慧, 朱景, 黄以平, 等, 2013. 基于多普勒天气雷达的火情自动识别系统[J]. 气象, 39(2): 241-248. DOI:10.7519/j.issn.1000-0526.2013.02.014 |
刘黎平, 牟容, 许小永, 等, 2007. 一次飑线过程的动力和微物理结构及滴谱变化对降水估测的影响研究[J]. 气象学报, 65(4): 601-611. DOI:10.11676/qxxb2007.055 |
刘淑媛, 孙健, 杨引明, 2007. 上海2004年7月12日飑线系统中尺度分析研究[J]. 气象学报, 65(1): 84-93. DOI:10.11676/qxxb2007.008 |
孙虎林, 罗亚丽, 张人禾, 等, 2011. 2009年6月3—4日黄淮地区强飑线成熟阶段特征分析[J]. 大气科学, 35(1): 105-120. |
王改利, 刘黎平, 2007. 暴雨云团的多尺度识别方法及其在临近预报中的应用[J]. 大气科学, 31(3): 400-409. |
王晓芳, 2012. 长江中下游地区梅雨期线状中尺度对流系统分析Ⅱ:环境特征[J]. 气象学报, 70(5): 924-935. DOI:10.11676/qxxb2012.078 |
王晓芳, 崔春光, 2012. 长江中下游地区梅雨期线状中尺度对流系统分析Ⅰ:组织类型特征[J]. 气象学报, 70(5): 909-923. DOI:10.11676/qxxb2012.077 |
杨吉, 刘黎平, 李国平, 等, 2012. 基于雷达回波拼图资料的风暴单体和中尺度对流系统识别、跟踪及预报技术[J]. 气象学报, 70(6): 1347-1355. DOI:10.11676/qxxb2012.113 |
张涛, 李柏, 杨洪平, 等, 2013. 三次雷暴导致的阵风锋过程分析[J]. 气象, 39(10): 1275-1283. DOI:10.7519/j.issn.1000-0526.2013.10.005 |
郑媛媛, 姚晨, 郝莹, 等, 2011. 不同类型大尺度环流背景下强对流天气的短时临近预报预警研究[J]. 气象, 37(7): 795-801. DOI:10.7519/j.issn.1000-0526.2011.07.003 |
郑祚芳, 高华, 李青春, 2013. 城市化对北京一次极端降水过程影响的数值分析[J]. 气象, 39(3): 340-346. DOI:10.7519/j.issn.1000-0526.2013.03.008 |
庄薇, 刘黎平, 薄兆海, 等, 2010. 新疆一次强飑线过程双多普勒雷达观测的中尺度风场结构分析[J]. 气象学报, 68(2): 224-234. |
庄薇, 刘黎平, 胡志群, 2013. 青藏高原零度层亮带的识别订正方法及在雷达估测降水中的应用[J]. 气象, 39(8): 1004-1013. DOI:10.7519/j.issn.1000-0526.2013.08.007 |
Chen G T J, Chou H C, 1993. General characteristics of squall lines observed in TAMEX[J]. Mon Wea Rev, 121: 726-733. DOI:10.1175/1520-0493(1993)121<0726:GCOSLO>2.0.CO;2 |
Diana L K, David R S, 1987. Gust Front Characteristics as Detected by Doppler Radar[J]. Mon Wea Rev, 115: 905-918. DOI:10.1175/1520-0493(1987)115<0905:GFCADB>2.0.CO;2 |
Dixon M, Wiener G, 1993. TITAN: Thunderstorm identification, tracking, analysis, and nowcasting radarbased methodology[J]. J Atmos Oceanic Technol, 1(6): 785-796. |
Geerts Bart, 1998. Mesoscale convective systems in the southeast united states during 1994-95: A Survey[J]. Wea Forecasting, 13: 860-869. DOI:10.1175/1520-0434(1998)013<0860:MCSITS>2.0.CO;2 |
Johnson J, Mackeen P A, Witt E M, et al, 1998. The storm cell identification and tracking algorithm: An enhanced WSR-88D algorithm[J]. Wea Forecasting, 13: 263-276. DOI:10.1175/1520-0434(1998)013<0263:TSCIAT>2.0.CO;2 |
Li P W, Wong W K, Chan K Y, et al.2000.SWIRLS——An Evolving Nowcasting System. Technical Note, No. 100. Hong Kong Observatory.
|
Lakshmanan V, Rabin R, DeBrunner V, 2003. Mutiscale storm identification and forecast[J]. J Atmos Res, 4: 367-380. |
Meng Z, Yan D, Zhang Y, 2013. General features of squall lines in East China[J]. Mon Wea Rev, 141: 1629-1647. DOI:10.1175/MWR-D-12-00208.1 |
Mueller C, Saxen T, Roberts R, et al, 2003. NCAR Auto-Nowcast System[J]. Wea Forecasting, 18: 545-561. DOI:10.1175/1520-0434(2003)018<0545:NAS>2.0.CO;2 |
Parker M D, Johnson R H, 2000. Organizational modes of midlatitude mesoscale convective systems[J]. Mon Wea Rev, 128: 3413-3436. DOI:10.1175/1520-0493(2001)129<3413:OMOMMC>2.0.CO;2 |
Rinehart R, Garvey E, 1979. Three dimensional storm motion detection by conventional weather radar[J]. Nature, 273: 287-289. |
 2014, Vol. 40
2014, Vol. 40