引 言

据不完全统计，我国约有水库8.6万座，流域在100~1000 km²的河流有5万多条，每年汛期防汛形势紧张，由于我国中小河流防洪标准普遍偏低，暴雨引发的中小河流洪灾损失约占全国水灾总损失的70%~80%(水利部水文局，2010；卞洁等，2011)。随着全球气候变暖，暴雨、强降水等极端事件增多，一旦降水量超过中小河流及水利设施的防洪承受能力，就会形成溃口、垮坝等，引发洪水，给下游地区和基础设施造成重大灾害。如“75·8”河南特大暴雨，导致板桥水库垮坝，造成2万多人死亡(章国材，2010)。因此，面对不断频发的暴雨灾害性天气给中小河流带来的巨大损失，有效确定中小河流及水利设施的临界面雨量已成为目前中小河流防洪减灾工作中的难点和重点。针对流域面雨量计算，水文气象工作者多以淮河、长江上游、海河等大流域为主，采用最优化订正法、泰森多边形法等，开展了大量研究和探讨(毕宝贵等，2003；周筱兰等，2003；王志等，2010；张亚萍等，2013)，其研究工作侧重于面雨量的制作和预报应用，对于如何有效确定流域(尤其是中小流域)临界面雨量也逐步引起了相关学者的重视(樊建勇等，2012；叶金印等，2014)，但仍有待进一步深入研究。为此，本文以湖北省荆门市漳河水库流域为例，结合其防洪能力，立足于水文模型，将其应用到该流域临界面雨量计算中，探索定量计算流域临界面雨量的新技术、新方法和新思路。

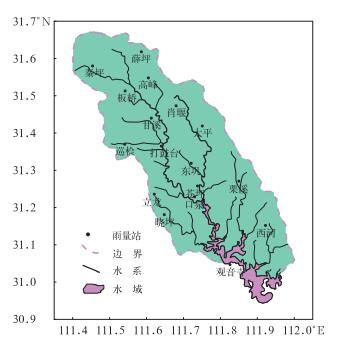
1 漳河流域概况及致汛临界雨量的确定与研究方法 1.1 漳河水库流域概况

漳河发源于湖北省南漳县境荆山南麓之三景庄，全长202 km，流域面积2980 km²，海拔高度42~1400 m。漳河水库位于湖北荆门市，其控制流域面积2212 km²，总库容20.35×10⁸ m³。流域内雨量站点分布均匀(图 1)，多年平均降水量989 mm(1963—2009年)，暴雨次数多、据有关统计资料，漳河下游堤防在1897—1958年期间，有40年出现堤坝决口，平均1.5年一次，给人民生命财产造成极大损失(赵金河等，2001)。

1.2 流域致汛临界雨量的统计计算

中小流域暴雨洪涝灾害是流域内强降水形成径流、汇流并远超过河流及水利设施防洪承受能力带来的结果。根据《漳河水库调度运用手册》可知，水库设计的汛期限制水位(以下简称汛限水位)为122 m，设计洪水位为125 m，校核洪水位为127.5 m。调查水库周边高程可知，122 m为水库周边平均海拔高度，如果以水库自然调蓄能力为限(超过该水位，需人工调蓄)，本文以汛限水位(122 m)作为漳河流域致汛临界水位(李兰等，2013)。

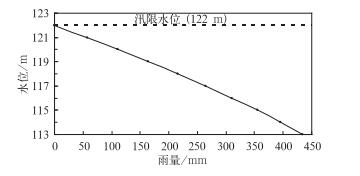
根据试验流域(漳河水库)水位库容关系，结合漳河流域气候特征，统计流域多年平均降水以及径流量，计算分析流域多年平均径流系数，结合水库水位-库容关系，按式(1) 推算相应的临界面雨量(长江流域规划办公室水文处，1980)，具体见表 1，并由此绘制漳河水库不同水位到达汛限水位所需的临界面雨量关系曲线(图 2)。

$P = 10W/aF$

(1)

式中，P为临界降雨量(单位：mm)，W为某一水位到达临界水位(汛限、设计等水位)尚可蓄水量(单位：10⁴ m³)，F为水库集雨面积(单位：km²)，a为径流系数。

由表 1、图 2可知，不同水位到达汛限水位(122 m)所需的面雨量是不同的。因此，在不同水位下，流域致汛临界面雨量(到达汛限水位所需的面雨量)不同。如果面雨量大于当前水位达到汛限水位所需的面雨量，流域就可能发生暴雨洪涝灾害。

1.3 水文模型推算临界面雨量技术思路

采用式(1) 计算的临界面雨量的方法简单、实用，其计算主要基于水均衡原理依靠径流系数、库容等信息来推算临界面雨量，未考虑降水时空分布、初始条件等因素对临界面雨量计算的影响。在此，本文以湖北省荆门市漳河水库流域为例，结合其防洪能力，立足于水文模型，运用水文模型模拟降水和流量关系，计算不同基础水位达到致灾标准所需要的雨量，通过假定不同的降水分布形态、设置不同的初始条件来探讨水文模型推算临界面雨量的方法，具体思路如下：

首先设定流域致灾标准(可参考《暴雨洪涝灾害致灾临界(面)雨量确定技术指南》(气减函〔2013〕113号))，并选定能代表流域洪涝灾害的控制水文站点(漳河水库控制流面积的3/4), 收集整理试验流域控制点的历史洪水过程以及相应的降水、流量等水文气象资料，根据试验流域气候特点确定水文模型，开展水文模拟试验以及参数率定工作。在此基础上针对漳河水库流域致灾(汛)标准(汛限水位122 m)，选择不同基准水位，将单位时间内(24 h)流域面雨量假定为不同的降水分布形态输入水文模型，进行汇流模拟，计算试验流域的洪水来水量、水位库容变化，从而确定不同降水分布条件下，不同基准水位到达汛限水位122 m所需的面雨量，即流域暴雨洪涝致灾(汛)临界面雨量。

2 水文模型选择及参数率定 2.1 模型选择

根据试验流域湿润的气候特点，本文选择在国内外水文预报工作中应用较好的新安江模型作为该流域水文预报模型。该模型使用了蓄满产流与马斯京根汇流概念，有分单元、分水源、分汇流阶段的特点，其结构简单、参数较少，各参数具有明确的物理意义，计算精度较高。模型通过将全流域分成多个单元流域，在每一个单元流域内，降水经过蒸(散)发的消耗后，以蓄满产流的方式经产流量水源划分后对各单元流域进行产汇流计算，得出单元流域的出口流量过程；再进行出口以下的河道洪水演算，将各个单元流域的出流过程相加，求得流域的总出流过程(赵人俊，1984；赵人俊等，1988)。

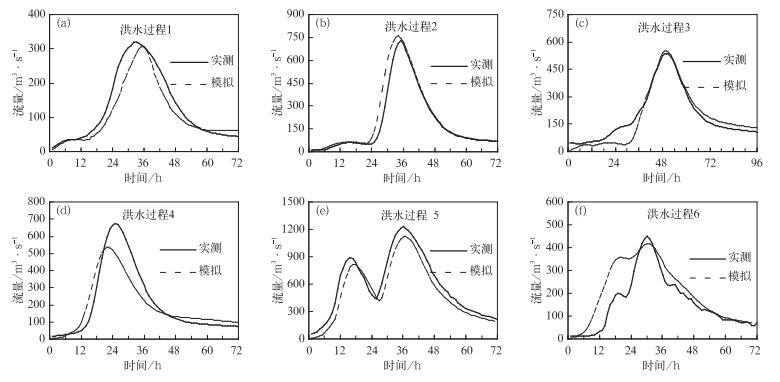
2.2 模型率定

在模型率定过程中，结合所收集到漳河水库坝前水文站资料，选取漳河流域1956—2012年36场洪水过程进行水文参数率定试验，其中30场洪水用作模拟计算流域水文模型参数，6场洪水用作参数验证。根据《水文情报预报规范》(SL25-2000)，对洪水试验预报结果，采用洪峰相对误差、峰现时差及模型有效性(即确定性系数)等指标来评定。模拟试验结果表明：漳河水库洪水模拟合格率达90%，效率系数为87.75(表 2)；其洪水过程验证模拟合格率达83.33%，效率系数为90.33%(表 3和图 3)。由此可知，通过水文模型模拟试验所率定的参数可用于水文预报和水文模拟试验(崔春光等，2010；彭涛等，2010a；2010b；殷志远等，2012；Peng et al，2011)。此外，水文模拟试验发现降水信息处理为单一面雨量的形式输入水文模型以及子流域的划分等因素对水文模拟效果存在影响。

3 漳河流域临界面雨量模拟计算 3.1 模拟条件设置

根据试验流域(漳河水库)水位库容关系表(表 1)以及流域降水径流过程规律(即最大降水发生至洪水过程结束持续时间约为24~48 h)，为此，以汛限水位122 m为临界水位，选择120、118、116和114 m为基准水位，以24 h为时限，将24 h流域面雨量输入水文模型，结合流域降水径流过程规律，取最大降水发生至洪水过程结束最大持续时间48 h，进行60 h汇流模拟，计算试验流域的水位库容变化，从而确定基准水位在120、118、116和114 m条件下的临界面雨量。

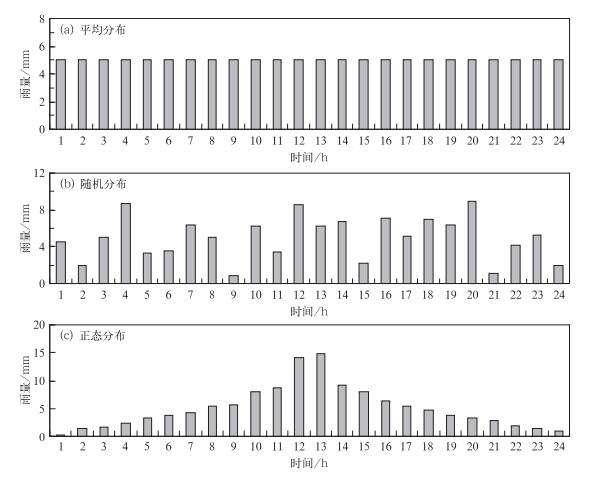
3.2 雨量分布形态假定

水文模拟实践表明：雨量时空分布不同，其模拟计算结果也不同。在试验流域临界面雨量模拟计算过程中，首先给出24 h流域的总面雨量(R₂₄)，基于数理统计理论分别假定24 h雨量呈平均、随机、正态三种分布(王金萍等，2010)。

(1) 平均分布。根据流域24 h总面雨量(R₂₄)，假定雨量在24 h内平均分布，则流域逐小时雨量(R_hi)为：

${R_{hi}} = {R_{24}}/24\quad\left( {i = 1,2,3, \cdots ,24} \right)$

(2)

(2) 随机分布。假定雨量在24 h内呈随机分布，首先利用C++语言随机函数产生24个随机数，再结合流域24 h总面雨量处理后，通过程序自动生成流域逐小时雨量R_hi，使其满足如下关系：

$\sum\limits_{i = 1}^{24} {{R_{hi}} = {R_{24}}} \quad{\mbox{且}}\quad {R_{hi}} \ne {R_{h(i - 1)}}\left( {i = 1,2,3, \cdots ,24} \right)$

(3)

(3) 正态分布。假定雨量在24 h内呈正态分布，根据正态分布密度函数，设计程序自动生成流域逐小时雨量R_hi，使其满足式(3) 及正态分布。

(4) 雨量分布模拟。根据雨量呈平均、随机、正态分布三种形态的假定，设置流域24 h总面雨量(R₂₄)为120 mm，则三种雨量分布形态见图 4。图 4中可知，当雨量呈正态分布时，能较好地刻画一场降水过程发生、发展、结束的过程。

3.3 水文模拟计算

根据三种假定的雨量分布形态求取流域24 h雨量分布，首先将24 h流域总面雨量R₂₄分别转化平均分布、随机分布、正态分布三种形态，然后输入水文模型，进行60 h汇流模拟计算，得到60 h入库流量变化曲线，在不考虑水库排水情况下按式(4)，根据60 h流量过程曲线计算水库的洪水来水量(即水库库容增量)，从而得到水库库容变化，再根据漳河水库水位-库容变化表计算得到漳河水库的水位变化。

${V_{\text{库容增量}}} = {V_{\text{来水量}}} = \int_{{t_1}}^{{t_2}} {{Q_{{t_i}}}{\rm{d}}t} $

(4)

式中，V_库容增量为水库不排水条件下t₁至t₂时刻库容增量，V_来水量为t₁至t₂时刻水库来水量，Q_ti为 t_i时刻的流量，t₁为初始时刻，t₂为截止时刻，文中t₂-t₁限定为60 h。

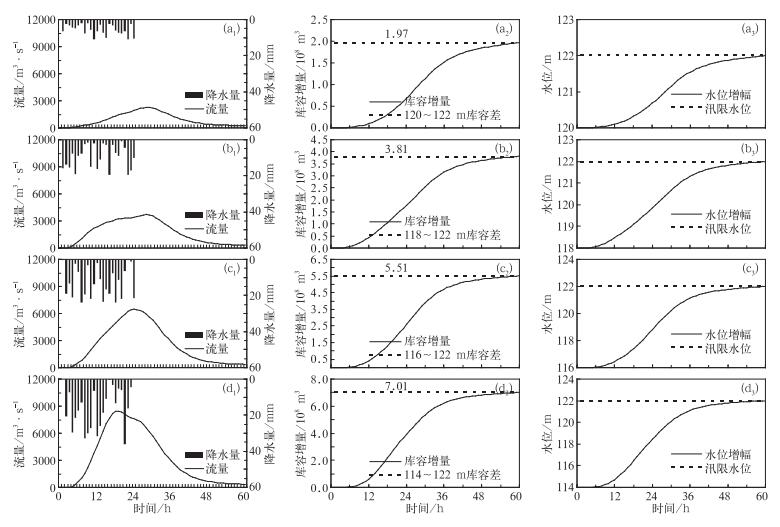
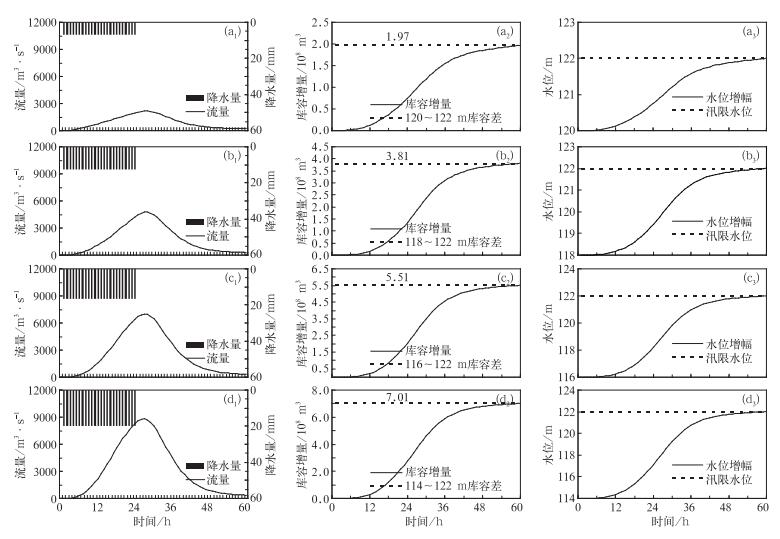
3.3.1 雨量平均分布

根据模拟试验计算结果，在降水平均分布条件下，水库基准水位为120 m时，当24 h累积降水量达到170 mm(平均每小时约7.08 mm)，根据60 h洪水入库过程曲线(图 5a₁)可计算得到60 h的洪水来水量(即库容增量)为1.97×10⁸ m³ (图 5a₂)，可使水位达到122 m (图 5a₃)；水库基准水位为118 m时，当24 h累积降水量达到304 mm(平均每小时约12.67 mm)，根据60 h洪水入库过程曲线(图 5b₁)可计算得到60 h的洪水来水量(即库容增量)为3.81×10⁸ m³ (图 5b₂)，可使水位达到122 m (图 5b₃)；水库基准水位为116 m时，当24 h累积降水量达到401 mm(平均每小时约16.71 mm)，根据60 h洪水入库过程曲线(图 5c₁)可计算得到60 h的洪水来水量(即库容增量)为5.51×10⁸ m³ (图 5c₂)，可使水位达到122 m (图 5c₃)；水库基准水位为114 m时，当24 h累积降水量达到472 mm(平均每小时约19.67 mm)，根据60 h洪水入库过程曲线(图 5d₁)可计算得到60 h的洪水来水量(即库容增量)为7.01×10⁸ m³ (图 5d₂)，可使水位达到122 m (图 5d₃)。

3.3.2 雨量随机分布

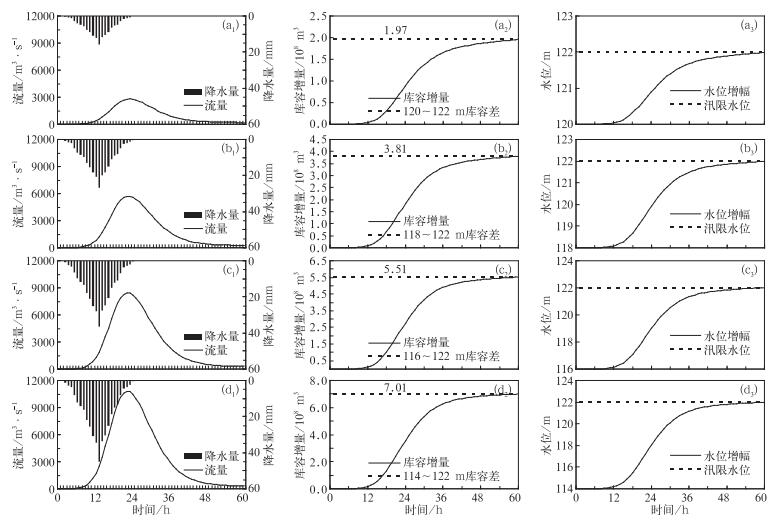
根据模拟试验计算结果，在降水随机分布条件下，水库基准水位为120 m时，当24 h累积降水量达到137 mm，根据60 h洪水入库过程曲线(图 6a₁)可计算得到60 h的洪水来水量(即库容增量)为1.97×10⁸ m³ (图 6a₂)，可使水位达到122 m (图 6a₃)；水库基准水位为118 m时，当24 h累积降水量达到231 mm，根据60 h洪水入库过程曲线(图 6b₁)可计算得到60 h的洪水来水量(即库容增量)为3.81×10⁸ m³ (图 6b₂)，可使水位达到122 m (图 6b₃)；水库基准水位为116 m时，当24 h累积降水量达到312 mm，根据60 h洪水入库过程曲线(图 6c₁)可计算得到60 h的洪水来水量(即库容增量)为5.51×10⁸ m³ (图 6c₂)，可使水位达到122 m (图 6c₃)；水库基准水位为114 m时，当24 h累积降水量达到379 mm，根据60 h洪水入库过程曲线(图 6d₁)可计算得到60 h的洪水来水量(即库容增量)为7.01×10⁸ m³ (图 6d₂)，可使水位达到122 m (图 6d₃)。

3.3.3 雨量正态分布

根据模拟试验计算结果，在雨量平均分布条件下，水库基准水位为120 m时，当24 h累积降水量达到130 mm，根据60 h洪水入库过程曲线(图 7a₁)可计算60 h的洪水来水量(即库容增量)为1.97×10⁸ m³ (图 7a₂)，可使水位达到122 m (图 7a₃)；水库基准水位为118 m时，当24 h累积降水量达到221 mm，根据60 h洪水入库过程曲线(图 7b₁)可计算60 h的洪水来水量(即库容增量)为3.81×10⁸ m³ (图 7b₂)，可使水位达到122 m (图 7b₃)；水库基准水位为116 m时，当24 h累积降水量达到303 mm，根据60 h洪水入库过程曲线(图 7c₁)可计算60 h的洪水来水量(即库容增量)为5.51×10⁸ m³ (图 7c₂)，可使水位达到122 m (图 7c₃)；水库基准水位为114 m时，当24 h累积降水量达到372 mm，根据60 h洪水入库过程曲线(图 7d₁)可计算60 h的洪水来水量(即库容增量)为7.01×10⁸ m³ (图 7d₂)，可使水位达到122 m (图 7d₃)。

3.3.4 结果分析

根据上述模拟计算以及图 6~8中曲线变化可知，漳河水库流域在降水平均分布、随机分布、正态分布情况下从114、116、118、120 m四个基准水位到达汛限水位122 m所需的临界面雨量分别为472、401、304、170 mm，379、312、231、137 mm，372、303、221、130 mm(表 4)。由表 4可知，雨量呈平均分布条件下到达汛限水位122 m所需的临界面雨量最大，随机分布次之，正态分布最小，雨量在正态分布与随机分布条件下两者临界面雨量相差不大，总体上正态分布略接近统计值。通过计算不同雨量分布形态下的临界面雨量与统计临界雨量的相对误差发现(表 4)，雨量平均分布条件下所模拟计算的临界面雨量与统计临界雨量差别较大，约19.19%~53.15%，雨量正态分布更接近降水的实际情况(即随降水发生，降水量逐步增大；随降水过程结束，降水量逐步减小)，所模拟计算的临界面雨量与统计临界雨量差别约2.57%~17.12%。

4 结论与讨论

本文以湖北省荆门漳河水库为例，结合漳河水库防洪能力，选取新安江水文模型，利用水文模型计算该流域致汛临界面雨量，得到如下结论：

(1) 中小河流暴雨洪涝临界雨量的计算是中小河流洪涝灾害预警及防御的基础条件，目前的中小河流临界雨量的计算方法及流程还在探索阶段，用水文模型推算中小流域临界雨量的方法是一种新的尝试。

(2) 新安江水文模型洪水预报试验结果表明，流域洪水过程模拟及验证试验的合格率及效率系数满足水文预报规范标准，通过水文模型模拟试验所率定的参数可用于水文预报及水文模拟试验。

(3) 运用水文模型推算临界雨量，能直观给出不同基准水位、不同雨量分布条件下的洪水入库过程曲线、水位变化过程曲线以及流域致汛临界面雨量，意义明确，技术方法可行。稳定性降水基本呈均匀性分布，对流性降水呈准正态分布，文中雨量平均分布及正态分布条件下所模拟计算的临界面雨量对实际指导性较强。

(4) 模拟计算表明，雨量呈平均分布条件下到达汛限水位122 m所需的临界面雨量最大，随机分布次之，正态分布最小，雨量在正态分布与随机分布条件下两者临界面雨量相差不大，总体上正态分布略接近统计计算值。

(5) 模拟研究发现，中小河流及流域临界面雨量不仅与水位有关，且雨量时空分布不同，其模拟计算结果也不同，雨量均匀分布，临界雨量唯一，雨量正态分布差异较小，雨量随机分布差异较大；其次，模拟计算的时效不同，其模拟计算结果也不同。针对试验流域，在考虑其历史真实的降水时空分布特点的状态下，按照其分布型计算不同雨型分布的临界雨量，会使结果更实用。

文中模拟计算的过程雨量无论是平均分布、随机分布还是正态分布均不是降水的实际分布，因此如何准确获取雨量的时空分布以及确定实际临界面雨量有待进一步完善和探讨；文中仅模拟计算24 h降水量与水位增长的关系，不同时长(6、12、18、24 h等)流域面雨量与达到致洪水位的水位增量的关系也有待进一步研究。此外，针对面积较小的山洪沟，因汇流时间短，相关基础数据缺乏，临界面雨量如何计算也有待进一步探讨。