引言

我国高原以东的夏季天气受到东亚季风进程影响。自陶诗言 (1996)总结1994年东亚夏季风活动异常与华南特大洪涝灾害；薛纪善 (1999)总结研究1994年华南夏季特大暴雨；周秀骥等 (2003)对1998年华南—江南暴雨的科学试验与研究；一般认为南海夏季风爆发受海洋 (水汽潜热与海气相互作用)、高原 (非绝热加热作用)、陆地 (陆面过程与陆气相互作用) 和极地 (冷空气活动) 等主要因素影响，夏季风按大尺度风场及水汽来源可分为印度、孟加拉湾季风和南海季风，前者较早爆发，且可以使得副热带高压断裂，后者的爆发与前者有关，但可以带来更多的水汽。张耀华等 (2012)研究认为，2010年夏季风具有明显低频振荡与季风涌特征。

吴尚森等 (1992)研究认为，一般随着夏季风爆发，华南—江南5月进入雨季，6月进入最大降雨量的汛期，之后降雨带推进到长江流域。梁建茵 (1994)分析华南前汛期旱涝等级年指出，6月副热带高压脊线偏北 (南) 与华南降水偏多 (少) 相对应。王东海等 (2011)对2008年华南—江南汛期先后4个暴雨过程作分析指出，低空环流决定雨区分布，南海季风涌为华南—江南输送水汽，我国华北、华东和华南为500 hPa位势高度负异常将有利于冷空气活动，而孟加拉湾为负异常有利于暖 (湿) 空气活动。姚才等 (2010)分析华南—江南6月降水极端年际差异认为, 来自南海的异常水汽输送具有重要影响。显然，分析大尺度环流仅能为一次特大暴雨提供有利背景。

特大暴雨一般是由中尺度对流雨团所导致。谌芸等 (2012)、王令等 (2012)对突发性特大暴雨作观测分析；王晓芳等 (2011)、尹洁等 (2011)、伍志方等 (2011)对华南—江南持续性大暴雨作诊断和模拟分析，但现阶段中尺度对流天气分析，主要是对暴雨的定性诊断分析，而定量诊断分析较少。例如，区别不清10~20 mm·h^-1暴雨和50~100 mm·h^-1特大暴雨。主观分析主要是天气分型和中尺度系统分析，如中尺度辐合线、中尺度涡旋等；客观分析主要是动力热力物理参数诊断分析，如不稳定能量、不稳定机制、垂直风切变 (shear) 等，还有一个用得较多、将不稳定能量和水汽结合的对流有效位能CAPE及里查森数 (Ri，Ri=CAPE/shear)，还有一些仅与暴雨间接有关的物理量，如位涡、螺旋度和Q矢量等。张小玲等 (2012)通过诊断计算中尺度对流系统发生的4个条件 (水汽、不稳定能量、抬升和垂直风切变)，开发出国家气象中心强对流天气预报系统。蒙伟光等 (2012)认为, 对流发展于有较大CAPE的区域。

李青春等 (2011)利用多普勒雷达、风廓线仪、微波辐射计和加密自动站资料，分析由近地层中尺度辐合线 (切变线) 引发的北京一次局地暴雨过程，认为利用常规气象资料，难以分析中尺度切变线上发生的局地暴雨，更不能预报暴雨的时间、落区与量值。王丽荣等 (2011)利用多普勒雷达资料，对一次石家庄γ中尺度大暴雨作分析认为，依据垂直累积液态水含量可提前18 min预报短时暴雨发生。葛晶晶等 (2011)用模拟作暴雨中尺度涡旋分析表明，暴雨是由低空急流大风速中心的非地转效应产生的重力波与中尺度涡旋作用激发出的β中尺度湿对流。林宗桂等 (2011)研究认为，中尺度对流系统可以在中尺度涡旋上发生并产生强降雨，中尺度对流系统发展的有利条件是：偏南暖湿气流输送水汽并造成位势不稳定，中尺度涡旋辐合上升运动抬升暖湿气流，对流单体沿切变线传播并入到中尺度对流系统。

现阶段随模式的时空分辨率提高，模拟暴雨从采用积云对流参数化方案 (隐式降水方案) 过渡到仅需采用云微物理方案 (显式降水方案)。郭肖容等 (1992)、史月琴等 (2006)研究认为，若是模式水平分辨率达到1~10 km，采用显式降水方案模拟云降水的物理作用空间逐渐扩大，即应由采用隐式降水方案，过渡到采用隐式和显式结合的混合降水方案，再过渡到单纯采用显式降水方案，使模式最有可能模拟中尺度雨团发生、发展与演变过程。

本文诊断分析2010年6月华南—江南持续性暴雨的大尺度水汽特征，又对其中的一次江南特大暴雨做中尺度数值模拟，并对模拟的中尺度暴雨雨带和雨团作高时空分辨率诊断计算，试图通过计算模式大气降水运动中的凝结函数降水率和水汽 (及云水、云冰、雨水) 通量散度降水率等，定性、定量分析特大暴雨形成的天气学成因。

1 降水过程诊断计算 1.1 凝结函数降水率和水汽、云水、云冰、雨水通量散度

按天气学，气柱可降水量 (H_q)、凝结函数降水率 (I_f) 和水汽通量散度 (I_q) 计算式分别为：

${H_q} = \int_{p_0}^{{p_s}} {q\frac{{{\rm{d}}p}}{g}} $

(1)

${I_f} = \int_{p_0}^{{p_s}} {F({q_s})\omega \frac{{{\rm{d}}p}}{g}} $

(2)

${I_q} = - \int_{p_0}^{{p_s}} {\nabla · ({\rm{V}}{q_s})\frac{{{\rm{d}}p}}{g}} $

(3)

式中，q(q_s) 为比湿 (饱和比湿)，F为凝结函数，ω为P坐标垂直速度，V=(u, v) 为水平风速，g为地球重力加速度，p为气压，并设积分下限为地面气压p_s、积分上限p₀取到100 hPa。但式 (2) 和 (3) 都只对相对湿度大于90%的近饱和层做垂直 (气压差) 积分。式 (2) 凝结函数降水率 (I_f) 由饱和气层压、温状态 (F) 与上升运动 (ω) 决定，当ω≤0时为上升运动，对I_f为“正”降水，同时保留ω > 0下沉运动时的“负”降水计算。而式 (3) 水汽通量散度 (I_q) 主要是由饱和气层的水汽通量散度决定，故在水汽辐合时，I_q为“正”降水，同时保留在水汽辐散时的“负”降水计算。

同理，比照式 (1) 和 (3)，还可以分别给出云水 (q_c)、云冰 (q_i) 和雨水 (q_l) 的总量及其通量散度计算式 (均略)，其物理机制是，饱和气层在辐合/辐散运动中, 因云水、云冰及雨水密度 (饱和度) 的变化而发生了“正”/“负”碰并增长或混合碰并增长。则可以计算出总水物质 (q_r, q_r=q_s+q_c+q_i+q_l) 的通量散度 (I_Q)：

${I_Q} = - \int_{p_0}^{{p_s}} {\nabla ·({\rm{V}}{q_r})\frac{{{\rm{d}}p}}{g}} $

(4)

又取“静力”垂直速度 $\left[ {\overline \omega } \right.$ ，对应式 (2) 有“静力”凝结函数降水率记为 $\left. {{{\overline I }_f}} \right]$ 为：

$\overline \omega = {(u\frac{{\partial p}}{{\partial x}} + v\frac{{\partial p}}{{\partial y}})_z} = - \rho g{(u\frac{{\partial z}}{{\partial x}} + v\frac{{\partial z}}{{\partial y}})_p}$

(5)

式中，ρ为空气密度，z为位势高度。

但一般各层垂直速度 (ω)，可因等压坐标连续方程，有诊断计算关系式：

$\omega = {\omega _s} - \int_{{p_s}}^p {(\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}})dp} $

(6)

取上式的地面层 (用下标s表示) 垂直速度 ${\omega _s} = - {\rho _s}g{(u\frac{{\partial z}}{{\partial x}} + v\frac{{\partial z}}{{\partial y}})_s}$ 。本文诊断计算表明，垂直速度ω比“静力”垂直速度 ${\overline \omega }$ ，随模式空间分辨率提高，一般要大1~4个量级。

因水汽、总水物质通量散度同为各层散度场[参见式 (3) 和 (4)]决定，故计算的水汽、总水物质通量散度降水率与凝结函数降水率[参见式 (2) 和 (6)]具有相近的垂直运动机制。

1.2 层结不稳定能量与理想对流可降水量

大气存在所谓的“条件不稳定”气块，可因气块 (设其所在气压高度为p) 的层结不稳定能量 (E_p) 释放，而造成该气块的上升运动与对流降水。因：

${E_p} = {R_{\rm{d}}}\int_{{p_t}}^p {({T_v} - {{\overline T }_v})} {\rm{dln}}p$

(7)

式中，T_v是气块 (湿绝热上升运动) 状态曲线上的虚温，而T_v是环境大气虚温，R_d是干空气比气体常数。则求取整个气柱的层结不稳定“正”能量 (E) 为 (因水汽主要存在于中低层，故实际积分气压差仅取p_s~400 hPa)：

$E = \int_{400}^{{p_s}} {{E_p}\frac{{{\rm{d}}p}}{g}} \ge 0\begin{array}{*{20}{c}} {}&{} \end{array}({E_p} \ge 0)$

(8)

这里，还可以定义与气块层结不稳定能量E_p相对应的理想对流可降水量 (H_e) 为：

${H_e} = \int_{400}^{{p_s}} {\delta (q - {q_s})} \frac{{{\rm{d}}p}}{g}$

(9)

式中，q_s为气块在上升运动状态曲线上的饱和比湿，q为其初值，则q-q_s > 0。且式 (9) 诊断计算是在E_p > 0并理想释放条件下，才相应取δ=1，否则取δ=0。显然，式 (9) 对流可降水量H_e，只是式 (1) 可降水量H_q中的一部分。

同理，可以诊断计算总水物质的对流可降水量，它也是总水物质中的一部分。

1.3 水汽通量和水汽权重平均风速

降水发生时的水汽输送，一般用水汽通量 (Q_q) 描述 (设V为气块水平全风速)：

${Q_q} = \int_{{p_0}}^{{p_s}} {{\rm{V}}q{\rm{d}}q} $

(10)

从而还可以定义[参见式 (1) 和 (10)]气柱的水汽权重平均风速 (V_q)：

${{\rm{V}}_q} = \frac{{{Q_q}}}{{{H_q}}}$

(11)

因大部分水汽存在于大气低层，故V_q实际反映所谓的“低空 (湿) 急流”。例如，当V_q>8(12) m·s^-1，即可判定为湿急流 (核)。

1.4 垂直运动与降水

大尺度天气系统 (如高空槽、高原槽、季风槽) 造成的缓慢爬升运动，可以是稳定性弱降水、或是强降水来临之前转“多云”的云水、云冰形成物理机制；而天气系统 (如西南涡、切变线、低空急流) 风场造成的中、小尺度垂直运动，才是模式大气显式降水、或者是启动层结不稳定能量释放与积云对流参数化降水的物理机制。显然，大尺度天气系统是中、小尺度垂直运动的背景场。

凝结函数降水率场是通过风场与散度场 (及地形) 先求垂直运动，再由凝结函数与垂直速度予以求得，它适当反映不同尺度天气系统中的垂直运动，具有风场中尺度特征，并描述降水运动的波动性，故凝结函数降水率能够解释中尺度雨团的显式降水物理成因。

水汽通量散度降水率场，默认风场辐合 (辐散) 即存在上升 (下沉) 运动，并且在饱和气层里形成“正”(“负”) 降水率；同理，云水、云冰、雨水通量散度分别是它们的密度发生正 (负) 变化，从而造成它们的“正”(“负”) 碰并增长或混合碰并增长，并且形成云水、云冰、雨水通量散度“正”(“负”) 降水率。因此，水汽及云水、云冰、雨水通量散度可以叠加，其中，各种液态、固态水物质的通量散度“正”降水率，可解释为大量云滴、冰晶、霰粒等，其在饱和对流云中因密度增加而迅速碰并增长为雨滴。

总之，垂直运动为降水之所必须。中尺度雨团既是在多尺度天气系统中发生，并且还是在有层结不稳定能量与凝结潜热释放，产生“对流运动”和“次级环流”，从而具有自增强机制，是在多尺度垂直运动的动态平衡中发展与消亡。

2 华南—江南持续暴雨大尺度水汽场特征 2.1 大尺度环流背景

2010年6月华南—江南大部及江南南部的降水偏多3成至1倍。该月500 hPa平均环流特征是：东亚中高纬度锋区及冷空气活动偏弱，东半球40°~60°N为位势高度正距平区，而“青藏高原—西南地区—长江流域”为东西走向负距平区，表明在我国的低纬带不断存在低值系统东移，西太平洋副热带高压偏强偏西，平均西脊点在110°E，有利于华南和江南出现持续性暴雨。

2.2 华南—江南暴雨大尺度水汽场诊断分析

利用国家气象中心提供T639逐日分析02、08、14和20时 (北京时，以下同)1°×1°压、温、湿、风资料，对2010年6月7—9、13—18和18—22日华南—江南持续性暴雨过程作诊断计算与分析表明，孟加拉湾和南海都是华南—江南持续性暴雨重要水汽源地，但南海水汽输送对于华南—江南暴雨更为直接，表现为每一次暴雨过程，都是季风槽带来孟加拉湾和南海上空的充沛水汽，即有可降水量的大值区 (50~60 mm) 登陆并向北漂移 (以上图略)。

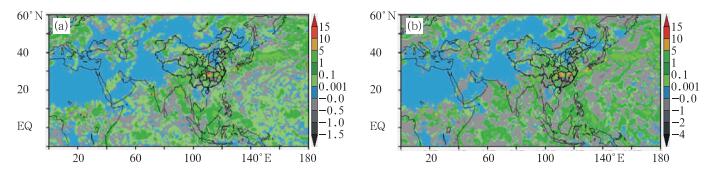
在整个华南—江南持续性降水时期，因大尺度天气系统 (如高空槽、高原槽)“静力”上升运动造成的凝结函数降水率 (I_f) 一般都小于1×10^-2 mm·h^-1，在暴雨区的最大值也仅达到3×10^-2 mm·h^-1(图略)；而按1°×1°分辨率风场诊断计算的上升运动及造成的凝结函数降水率 (I_f)，一般能达到0~5 mm·h^-1，其在暴雨区也只能达到5~15 mm·h^-1或稍大，表明它更多、更广地只是形成了降水上游区的大范围 (云水、云冰) 波状云系 (图 1a)，以此成为更加有效的水物质通量；同时计算的水汽通量散度降水率I_q与I_f量级相当，即是它们的大小和范围相当接近 (图 1b)，但它们不会相等。

以上诊断分析还表明，虽然高空槽前暖湿气流整体处于大尺度辐合抬升状态，但只有在“西南涡—切变线”天气系统上升运动区，才出现中、小尺度暴雨雨带和雨团。那么，6月18—22日特大暴雨的天气学成因，有待于作中尺度数值模拟与降水运动诊断分析。

3 特大暴雨中尺度数值模拟 3.1 模拟方案

WRF (Weather Research and Forecasting) 中尺度数值模式系统是美国多个部门联合开发的新一代细网格中尺度预报模式和同化系统。模式设计为非静力动力框架，水平分辨率可达到1~10 km。本文模拟采用了地形追随静力气压 (质量) 欧拉坐标、水平Arakawa C格式与双向嵌套等。

采用WRF模式 (WRFv3.4.1版本)，用T639资料做初边场，对华南—江南持续暴雨过程中发生在江南南部的最强一次暴雨过程作数值模拟，模拟时间是6月19日02时至20日14时，积分36 h。模拟区域网格结构采用三重嵌套：DOM1、DOM2和DOM3，模拟区域中心设在 (28°N、117°E)，水平分辨率 (格距) 分别为36、12和4 km，格点数分别为201×201、187×187和187×187，垂直分层均为35层，时间步长分别为120、40和12.33 s。DOM1和DOM2区域采用Ferrier (new Eta) 云微物理方案和Betts-Miller-Janjic积云对流参数化方案的混合降水方案；DOM3区域采用Ferrier云微物理显式降水方案。并均采用Dudhia云辐射短波辐射方案，rrmm长波辐射方案，YSU边界层方案和热量扩散陆面过程方案等。

3.2 模拟检验

6月18—22日，华南—江南暴雨逐渐北移，江南大部及广西出现大到暴雨，其中江西中北部、湖南中北部和福建中北部出现大暴雨到特大暴雨。

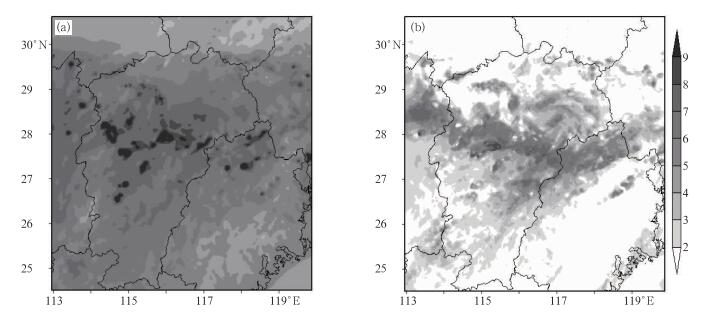
DOM1、DOM2、DOM3基本模拟出“高空槽 (引导)、西南涡 (东移)、切变线 (随冷空气南压)、低空急流 (湿空气辐合)”强降雨过程和发生在湖南、江西和福建的“左”、“中”、“右”三个中尺度暴雨中心 (DOM3参见图 2a和2b)，其模拟降水量一般在150~300 mm。实况强降雨主要集中在江西中部至福建北部，对应于“中”、“右”模拟暴雨中心，对应实况降水量一般在250~400 mm。例如在19日08时至20日08时的24 h降水量，江西进贤329 mm、东乡328 mm、余江321 mm、资溪318 mm、南昌278 mm、福建武夷山324 mm、光泽268 mm、湖南汨罗196 mm、平江175 mm。参见图 2c和2d，在19日12—13时的1 h降水量，江西余江58.4 mm、进贤49.7 mm、修水41.9 mm、南昌40.9 mm、东乡38.3 mm，而DOM3的1 h模拟降水量在江西中部也有一个暴雨中心，且模拟降水量与实况较为接近，但模拟暴雨中心的平均位置较实况偏南约20~30 km。

本文对模拟模式大气，作高时空分辨率的降水运动诊断计算与分析，即对DOM1、DOM2和DOM3的36 h模拟作每小时诊断计算，而对DOM3的1 h模拟作每2 min诊断计算，用以分析从α中尺度 (200~2000 km) 到β中尺度 (20~200 km) 到γ中尺度 (2~20 km) 暴雨雨带和雨团。

4 特大暴雨中尺度模拟诊断分析 4.1 水汽和总水物质

DOM1、DOM2和DOM3模拟的可降水量，在低层切变线α中尺度辐合饱和区一般可以达到60~70 mm (图略)，而对应的总水物质 (水汽+云水+云冰+雨水) 可降水量在β中尺度至γ中尺度辐合饱和区可增加达到70~90 mm亦或更大 (图 3a)，且辐合高湿区随天气系统移动，表明在高空槽前，可以有大量云水、云冰聚集到“西南涡—切变线”辐合区当中；同时，在辐合饱和区的层结不稳定能量可达到30~40 J·cm^-2(图略)，与不稳定能量相对应的对流可降水量在α中尺度辐合大值区达到40~60 mm (图略)，而总水物质对流可降水量在β中尺度至γ中尺度辐合区增加达到60~80 mm (即6~8 g·cm^-2, 图 3b)。分析表明，模拟“西南涡—切变线”暴雨一般只发生在总水物质对流可降水量大值区或大值区轴线下游方。

DOM1、DOM2和DOM3均模拟出切变线南侧存在的低空湿急流 (图略)，其水汽通量达到900~1200 kg·m^-1s^-1)，从而表明，暴雨上游区存在所谓的“水汽 (通量) 急流带”，但中尺度暴雨一般只发生在水汽强辐合区，即只出现在水汽急流轴的下游方，而不直接出现在水汽急流带上。

4.2 最大可能对流可降水率

由前述对流可降水量 (H_e)，可估算一个中尺度雨团的最大可能对流可降水率。这里，若给出中尺度 (Δx) 范围，且以前述水汽权重平均风速 (V_q) 穿过Δx所需时间，作为重建中尺度高湿区的水汽权重平均时间 (设为S，S=Δx/V_q)，则其最大可能对流可降水率 (I_e) 为：

${I_e} = \frac{{{H_e}}}{S} = \frac{{{H_e} · {{\rm{V}}_q}}}{{\Delta x}}$

(11)

式 (11)I_e是在理想过程 (充分的上升运动与层结不稳定能量完全释放) 条件下，气柱的对流可降水量全部作为降水之降水率。例如，设气团的平均对流可降水量为40~80 mm，其水汽权重平均风速为8~12 m·s^-1，对应于不同的中尺度雨团Δx=72、24、8 km (72、24、8 km分别为DOM1、DOM2、DOM3二倍格距)，其最大可能对流可降水率分别为I_e=16~48，48~144，144~432 mm·h^-1。显然，这里是将中尺度暴雨理想地描述为有湿急流 (核) 配合、出现在层结不稳定气团当中的理想中尺度对流雨团。

诊断计算表明，模拟的“西南涡—切变线”特大暴雨，所估算的β中尺度和γ中尺度暴雨雨团的最大可能对流可降水率与实况降水在强度 (量级) 上相接近，故定性诊断分析中尺度雨团的对流可降水率，可以释用于雷达临近预报。

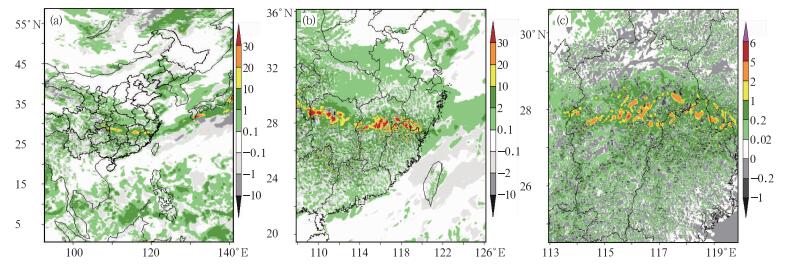
4.3 凝结函数降水率和总水物质通量散度降水率

由DOM1、DOM2和DOM3模拟的凝结函数降水率场 (图 4a~4c) 看出，模式较好地模拟出“高空槽带动低层弱冷空气活动—冷式切变线南压—西南涡东移”等不同尺度天气系统演变过程。通过诊断计算格距分别为36、12和4 km的散度场与垂直运动，DOM1模拟出切变线附近凝结函数降水率为10~20 mm·h^-1的α中尺度雨带，DOM2模拟出切变线辐合饱和区中有凝结函数降水率为10~30 mm·h^-1的β中尺度暴雨雨团，DOM3更模拟出“瞬间”凝结函数降水率为3~6 mm·(2 min)^-1(60~180 mm·h^-1) 亦或更大的γ中尺度暴雨雨团。

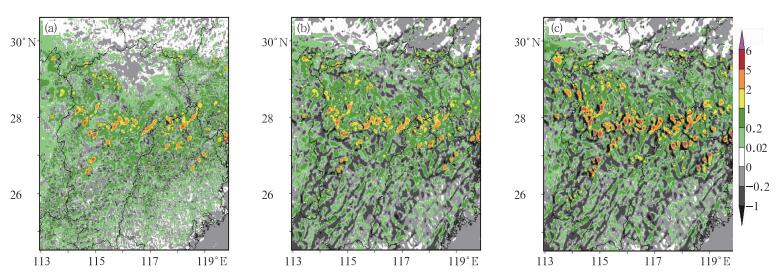
进一步对DOM3模拟所作高时空分辨率的诊断分析表明 (图 5a)，经由水平格距为4 km、垂直分35层所描述的风场垂直运动，已经能够模拟出在850 hPa切变线与低空急流之间的暴雨发生区内，不断有凝结函数降水率为1~6 mm·(2 min)^-1的γ中尺度雨团形成与演变，它们在传播过程中，或增强或减弱、或合并或分裂、或新生或消亡，并且其凝结函数降水率与实况降雨强度 (小时降雨量) 大致相近，故本文认为，DOM3已“仿真”模拟出中尺度对流系统 (MCSs) 及其多个γ中尺度对流单体的活动。

DOM1、DOM2和DOM3模拟的水汽通量散度降水率场 (DOM3参见图 5b) 与对应的凝结函数降水率场及其演变相似，但比较而言，前者在诊断时刻 (一个时间步长) 较准确描述各层的水汽辐合 (散) 运动，后者较准确描述气团温湿状态及整体垂直运动，经由图 5a和5b比较，两个降水率虽在模拟中尺度雨团强度和范围上均较为接近，但在0~1 mm·(2 min)^-1的较弱降水率区有较多的差别，因按连续方程，诊断计算各层的水汽通量散度场，其辐合或辐散强度和范围对等，故水汽通量散度降水率场具有较多虚假的“负”降水区，而凝结函数降水率场是由各层连贯的垂直运动引起，故而较为真实。

由DOM3模拟的总水物质通量散度降水率场 (图 5c) 看出，因其合理考虑云水、云冰和雨水的密度变化与碰幷增长，它们在辐合饱和区雨团 (积雨云) 中，其比单纯水汽通量散度降水率要大1~2 mm·(2 min)^-1(30~60 mm·h^-1) 亦或更大的降水率。显然，这里的水物质碰幷增长，造成附加降水率，是中尺度特大暴雨形成的另一个重要天气学成因。

4.4 显式降水和积云对流参数化降水

以上诊断分析表明，三重嵌套WRF模式较好地模拟出“高空槽—西南涡—切变线—低空急流”天气系统造成在江西、福建和湖南发生的特大暴雨过程，随着嵌套模式时空分辨率提高，模拟由气团温湿状态与垂直运动决定的凝结函数降水率，已经逐渐逼近于模式的显式降水物理过程；而模式大气当中各种水物质碰幷增长形成的附加降水率，则可以通过它们的通量散度予以描述。从而表明，模拟中尺度暴雨雨团发生、发展的天气学动力因素，应是高时空分辨率风场 (运动方程) 及散度场 (连续方程)，以及垂直运动与地形 (地形决定地面风垂直速度)，其与涡度、位涡度、螺旋度和Q矢量等并无直接关系，当然，中尺度雨团降雨强度还与气团温湿度 (热力学方程) 及气层稳定度 (非静力) 有关，所以，显式降水总是难以排除不稳定气层中，可能发生的中、小尺度垂直对流运动与积云对流参数化降水。

因诊断计算凝结函数降水率的垂直运动，不包含因层结不稳定能量释放造成的垂直对流运动，后者是对天气系统垂直运动的必要补充，故凝结函数降水率只描述与模式时空分辨率相适应的显式降水部分，而上述估算的最大可能对流可降水率，当属于隐式降水部分。所以，当模式时空分辨率较低时 (如DOM1和DOM2)，必须要用积云对流参数化描述降水，即在一个时间步长、一个网格内可以有积云对流活动，层结不稳定能量及凝结潜热一并得到释放，同时产生“参数化”降水。即便是在DOM3模式大气中，在其一个时间步长 (12.33 s) 和一个网格 (4 km) 内，其“参数化”降水空间越来越小，但仍然存在因不稳定能量释放而造成的对流运动与“参数化”降水间隙。同时，模式也未必能完全考虑好复杂地形对于垂直运动的作用，故模拟中、小尺度对流雨团及降水，尚待进一步研究。

5 结论与讨论

(1) 对2010年6月华南-江南持续暴雨作了T639模式大气的降水运动诊断分析，华南—江南持续性暴雨的水汽场特征是，因低纬大气系统 (季风槽等) 异常活动，造成孟加拉湾和南海上空大尺度水汽进入大陆，高空槽前大尺度上升运动是低层切变线中、小尺度雨团形成的背景场，“高空槽—西南涡—切变线—低空急流”系统在聚集水汽的同时，还聚集大量的云水和云冰等，它们一起成为更加有效的总水物质可降水量通量，而暴雨发生在上游区有湿急流、并且处于风场辐合的总水物质大值区与对流可降水量大值区。

(2) 用WRF中尺度模式模拟6月19日02时至20日14时江西、福建和湖南特大暴雨过程，并作了高时空分辨率三重嵌套模式大气的降水运动诊断分析，模拟出“高空槽引导—西南涡东移—切变线随冷空气南压—低空湿急流”造成的α中尺度暴雨雨带和雨带中的三个β中尺度暴雨中心，以及连续发生、发展于其中的γ中尺度暴雨雨团 (单体)。

(3) 诊断分析凝结函数降水率表明，格距为36 km的DOM1只模拟出10~20 mm·h^-1的切变线α中尺度雨带，格距为12 km的DOM2可模拟出10~30 mm·h^-1的β中尺度暴雨中心，而格距为4 km的DOM3可模拟出2~6 mm·(2 min)^-1亦或更大降水率的γ中尺度暴雨单体，在江西中北部发生特大暴雨时，DOM3模拟雨团的凝结函数降水率与实况降雨强度相接近，这表明随模式时空分辨率提高，模拟的凝结函数降水率逐渐逼近于模式的显式降水物理过程。

(4) 诊断分析总水物质通量散度表明，云水、云冰通量散度，其物理机制是它们在饱和云团中因密度变化而发生碰并增长，它们可形成1~2 mm·(2 min)^-1附加降水率，并且应与同时发生的凝结函数降水率相叠加，一起成为显式降水 (率)。

(5) 即使模式水平分辨率达到4 km、时间步长达到12.33 s，其中仍然会有一定做积云对流参数化降水的空间，即仍然有层结不稳定能量释放、并产生对流运动与维系中、小尺度对流降水的间隙，但气团中总水物质守恒，故积云对流参数化只影响局地降雨时空分布，对降雨总量影响不大。