引言

目前，提高短期气候预测水平的常用方法有两种：一是对数值模式结果进行统计降尺度或动力降尺度应用，其预报效果的好坏依赖于数值模式预测结果的优劣。二是依靠改进统计方法，虽然统计方法存在着某些局限性和不稳定性，比如历史样本的有限性，统计方法无法对历史上没有出现过的气候异常强度和分布做出预测，历史资料得到的统计关系随着气候的长期变化也在不断的改变，甚至很多关系目前已经变得不如当初发现它们时显著。但是，由于数值预报水平发展仍有待提高，研究和发展新的统计方法仍是提高省(市)短期气候预测水平的有效途径之一。

短期气候预测中引入的经典数学方法大多是针对线性和平稳时间序列进行分析的，而气象问题本质上都是非线性的，因而对于气象要素序列中很多非平稳和非线性过程不能较好地提取出有用的信息。经验模态分解(Empirical Mode Decomposition，EMD)，即逐级进行平稳化处理，把不同周期的波动从原信号中分离出来，且该波动是平稳的，称该波动为本征模态函数(Intrinsic Mode Function，IMF)，不同的IMF分量是平稳信号，具有非线性特征和缓变波包的特征。另外，EMD方法依据数据自身的时间尺度特征来进行信号分解，无须预先设定任何基函数，这一点与建立在先验性的谐波基函数和小波基函数上的傅里叶分解与小波分解方法具有本质性的差别。因此，EMD方法在处理非平稳及非线性数据上，具有非常明显的优势(张明阳等，2007)。EMD方法及相应的Hilbert变换正成为处理非线性、非平稳时间序列的有力手段，并已在生物、海洋、大气科学、天文学和工程技术等领域中得到了初步应用(林振山等，2004；郑祖光等，2010)。许多气象学家开展了基于EMD方法对各种气象资料时间序列的分析工作，主要包括：MJO(Love et al, 2008)、降水(McMahon et al, 2008)、气温(方仕全等，2005；邹明玮，2007；玄兆燕等，2008a; 2008b)、降水日数(毕硕本等，2010)、副热带大气系统(侯威等，2006)、成灾面积(刘莉红等，2008)、海平面高度(刘莉红等，2010b)、大气边界层高度(刘莉红等，2010a)和海水温度(杨周等，2010)。但是把这种方法初步应用到预测的研究主要有：万仕全等(2005)和邹明玮(2007)以扬州530年(1470—1999年)旱涝级别序列和北半球1995年(1—1995年)树木年轮序列为例，采用EMD方法、均生函数和最优子集回归方法构建了一个新的预测模型，结果表明，特征IMF分量有较高的可预测性，它对原序列趋势的预测有重要指示意义。玄兆燕等(2008b)采用EMD和神经网络方法相结合对石家庄的气温和降水进行预测，结果得到EMD方法降低了被预测信号中的非平稳性，其预测精度比直接用神经网络预测的预测精度有较明显的提高。这些研究(万仕全等，2005；邹明玮，2007；玄兆燕等，2008a; 2008b)采用实例数据在预测方面做了初步尝试，这为气候预测开辟一条新的有效途径。

另一方面，随着科技的发展，集成方法已经成为当前气候预测中的关键技术，尤其是气候模式发展的重要方向(陈法敬等，2011；尤凤春等，2009；狄靖月等，2013；纪永明等，2011)。然而，目前大部分气象部门预测方案都是采用单一的数理方法来构建模型，由于使用的预测手段不同，考虑影响气象要素的物理因素不同，各种预报方法得到的预报结果也不尽相同或存在很大差异，但都能在一定程度上提供一些有用的信息。因此，若采用一种客观方法将各种预报结果加以集成，可提高对气象变量的短期气候预测准确率(魏凤英，2007；2011)。雷向杰(2011)基于多元回归预测法、月际持续性预测法、年际持续性预测法和基于EOF的Downscaling法共4种方法建立了集成预测模型，结果得到集成预测方法的效果明显优于单一预测方法。毕硕本等(2012)采用EMD对广西2月气温序列进行分解，然后对得到的IMF分量构建集成预报成员，用均生函数逐步回归法对各集成成员进行预测，结果表明加入EMD算法和集成预报技术的方法比单一预测方法具有更好的预测能力。从而可见，集成方法的引入可有效改进短期气候预测效果。

本文引入EMD方法对广东降水时间序列进行多时间尺度分离，将复杂的非平稳信号简化为相对简单的不同时间尺度振荡的准周期信号，选取能较好描述降水周期特征的IMF分量作为预测模型的备选因子，然后分别采用均生回归、均生相关、韵律拟合误差和拟合误差4种方法对选取的备选因子构建预测模型。最后，参照雷向杰(2011)的研究方法，再以这4种预测模型为备选因子，采用多元线性回归方法构建集成预测模型。与毕硕本等(2012)研究不同的是，他们是对IMF分量构建集合序列，即考虑了初值的集合，本文是对预测方法进行集成，即考虑了预测模型的集成。本研究期望引入EMD方法和回归集成预测模型能提高广东降水的短期气候预测水平，为政府决策部门提前做出准确的指导。

1 资料和方法 1.1 资料处理

降水和气温数据是由广东省气候中心提供的1961—2011年广东86个台站的逐月降水和气温观测资料，以1981—2010年作为气候平均值。

用于降水和气温检验的方法为2010年中国气象局国家气候中心《短期气候预测质量分级检验办法》中的Ps六级评分方法。

1.2 研究方法

本文采用相关分析、经验正交函数(EOF)、EMD、均生回归、均生相关、韵律拟合误差、拟合误差、多元线性回归和回归集成等方法对资料进行处理、多时间尺度分离和模型构建。其中，均值生成函数(魏凤英等，1990)(Mean Generating Function, MGF)，提出了视MGF为原序列生成的、具有周期性的基函数的新构思，设一时间序列x(t)：

$ x\left(t \right) = \left\{ {x\left(1 \right), x\left({2} \right), \cdots, x\left(n \right)} \right\} $

(1)

式中, n为样本量。

x(t)的均值为：

$ \overline x = \frac{1}{n}\sum\limits_{i = 1}^n {x\left(i \right)} $

(2)

对于式(1) 定义均值生成函数：

$ \overline x \left(i \right) = \frac{1}{{{n_l}}}\sum\limits_{i = 0}^{{n_l} - 1} {x\left({i + jl} \right)} \;\;\;\;\left({i = 1, \cdots, l, 1 \le l \le m} \right) $

(3)

式中n_l=INT(n/l)，m=INT(n/2) 或INT(n/3)，INT表示取整数。根据式(3)，可以得到m个均生函数，将均生函数定义域延拓到整个数轴上，即作周期性延拓，构造均生函数延拓矩阵。而均生回归法，即先把降水序列作均生延拓，对得到的所有均值生成函数因子，采用多元线性回归方法(魏凤英，2007；吴诚鸥等，2007；黄嘉佑，2004)建立预测模型。另外，均生相关法，即先把降水序列作均生延拓，再对延拓结果与原序列计算相关，取2~7、7~15和15~N/2年间(N为序列长度)的延拓序列高相关的3个因子，即找到长、中、短3个不同尺度因子，采用多元线性回归方法建立预测模型。韵律拟合误差法参见魏淑秋(1985)工作。拟合误差法参见谢小康(1994)工作。本文主要采用EMD(郑祖光等，2010)方法对各月、季降水序列进行多时间尺度分离，分别采用均生回归、均生相关、韵律拟合误差和拟合误差4种方法对基于EMD得到的IMF分量构建月、季降水预测模型。

2 基于EMD算法的多时间尺度信息提取及集成模型构建 2.1 基于EMD算法的多时间尺度信息提取

长时间的降水序列本身蕴含了其多重周期演变特性，但由于影响降水系统的复杂性，使该序列包含了许多非平稳和非线性信息，如何从中提取出具有预测指示意义的周期特征，是众多研究者关注的重点之一，EMD工作在尺度分离工作中的优势已被一些学者证明。

对广东各月或季降水序列进行标准化，然后用EMD方法分解，通常能得到5~6个IMF分量和1个趋势项，计算各IMF分量与原序列的相关系数，以及IMF分量所占方差贡献，选取相关系数高、方差贡献大的IMF因子作为2.2节建模的备选因子。

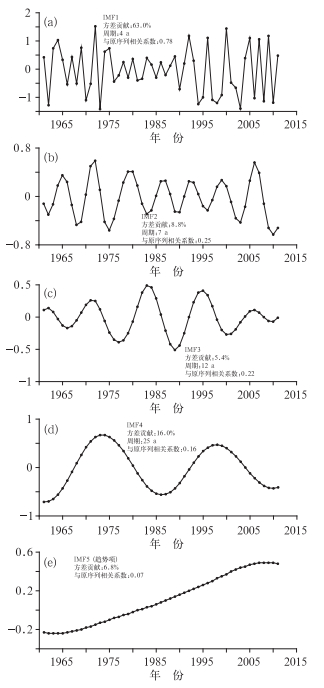
选取广东汛期(4—9月)降水为例进行EMD分析。首先，对1961—2011年广东汛期降水进行EMD，得到4个IMF分量和1个趋势项(图 1)。在构成广东汛期降水量变化的4个不同时间尺度的波频中，IMF1与原序列相关系数为0.78，其周期分别表现为4 a，而IMF2、IMF3和IMF4的相关系数分别为0.25、0.22和0.16，周期分别为7、12和25 a，最后一项IMF5为趋势项，与原序列相关系数为0.07，表现为自20世纪60年代中期以来广东汛期降水一直呈现上升趋势，但近5年增加趋势不明显。

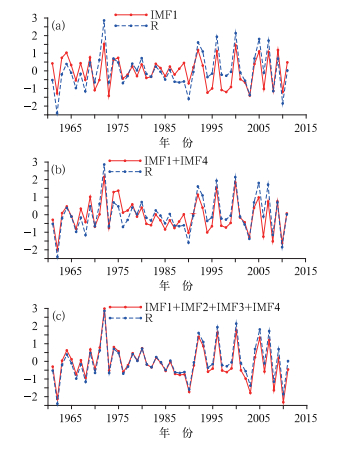
计算各IMF分量的方差贡献得到，IMF1占方差的贡献达63.0%，比较IMF1分量与原序列(图 2a)，可以看出IMF1基本能拟合出原序列，说明汛期降水主要以4 a振荡为主。IMF1和IMF4这2个分量累积方差贡献达79%，取这两个IMF分量合成与原序列曲线的对比(图 2b)，可以看出合成曲线基本包含了原序列信息，与原序列相关系数高达0.88，即在IMF1分量中加入25 a长周期的IMF4分量，其合成效果较图 2a更好。若取IMF1~IMF4，则累积方差贡献达93.2%，与原序列相关系数高达0.97，其重构值与原值非常接近，可见EMD方法分离出多时间尺度信息基本能重构原信息的特征。

2.2 基于多尺度信息的统计模型构建

对基于EMD方法得到具有较高相关系数和较大方差贡献的IMF分量，分别采用均生相关法、均生回归法、韵律误差法和拟合误差法构建降水的预测模型，建模年份为1961年至预测前一年，回报检验时采用逐年向前滚动检验法。其预报结果如表 1和表 2，可以看出4种预测方法对近10年广东汛期降水的Ps评分平均值在68~73分之间，而降水距平同号率评分的平均值在50%~58%。与原降水序列构建模型相比(表略)，多时间尺度各单一预测模型均有不同程度的提高，Ps评分增加了3分，同号率评分增加了5%，可以看出若剔除了原序列中的噪音，在一定程度上能有效改进预报效果。

2.3 基于回归方法的集成预测模型构建

集成预报的基本含义是将两个以上模型的预报结果用统计方法集成为单一的预报结果。集成预报的关键是如何确定权重系数。通常采用简单的算术平均或根据各种方法事先人为设定历史预报技巧或用回归系数给各种预报方法不同的权重。在预报样本量不是足够大的情况下，算术平均通常不能得到最优集成预报。在有限样本情况下，回归系数可以保证在最小方差意义下得到最优集成拟合(魏凤英，2007)，因此本文选取回归集成法(朱伯承，1981)构建预测模型。回归集成法将n种原始预报模型y₁, y₂, …，y_n作为新的预报因子，求预报量实况值y的回归方程：

$ p = {a_0} + {a_1}{y_1} + {a_2}{y_2} + {a_3}{y_3} + {a_4}{y_4} $

(4)

其系数满足如下线性方程组

$ \left\{ \begin{array}{l} {s_{11}}{a_1} + {s_{12}}{a_2} + \cdots + {s_{1n}}{a_n} = {a_{1y}}\\ {s_{21}}{a_1} + {s_{22}}{a_2} + \cdots + {s_{2n}}{a_n} = {a_{2y}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {s_{n1}}{a_1} + {s_{n2}}{a_2} + \cdots + {s_{nn}}{a_n} = {a_{ny}}\\ {a_0} = \overline y - \left({{a_1}{{\overline y }_1} + {a_2}{{\overline y }_2} + \cdots + {a_n}{{\overline y }_n}} \right) \end{array} \right. $

(5)

其中：

$ {s_{iy}} = \sum\limits_{k = 1}^M {\left({{y_{ik}} - {{\overline y }_i}} \right)} \left({{y_k} - {{\overline y }_j}} \right) $

式中，M为预报次数，y_ik为第i种原始预报方法所作的第k次预报值，y_k为第k次实况值。将式(5) 的解代入式(4) 便得回归集成预报方程。

本文选取均生相关y₁、均生回归y₂、韵律误差y₃和拟合误差y₄共4种预报模型作为集成成员的备选因子，采用多元线性回归方法构建如式(4) 的集成预测模型。取4种单预测模型预测年份前10年的回报值代入式(5)，得到a₀, a₁, a₂, a₃和a₄5个系数的解，代入式(4) 即得到回归集成预测模型。该集成预测模型是动态的，各台站的回归系数随预测对象(降水或气温等)、预测年和预测时段(季、月及旬等)的变化而动态改变。以汛期降水为例，取2002—2011年86个台站近10年4种单预测模型的回报值代入式(5)，分别计算得到各台站的5个回归系数，表 3列出任意5个台站的a₀, a₁, a₂, a₃和a₄回归系数，可以看出在不同的台站预测过程中各种预测模型发挥着不同的作用，效果各有优劣。

对回归集成方法近10年广东汛期进行回报(表 1和表 2)，可以看出回归集成的效果明显优于各单独预测模型，Ps评分的平均值上升到79.8分，较单一模型中最优的均生回归法增加了6.9分，降水距平符号同号率平均值为68.8%，较单预测模型增加了10%以上。较原降水序列回归集成模型(表略)，其Ps评分和同号率评分分别增加了10分和10%以上，说明开展物理模型的集成预测，能有效提高短期气候预测水平。

进一步分析各预测模型的空间预测效果，以2012年汛期为例，对广东86站降水进行EMD分解后，选取特征IMF分量，分别采用均生相关法、均生回归法、韵律拟合误差法和拟合误差法构建模型进行预测，得到如图 3所示结果，实况的分布为广东省大部分降水偏少，各单预测模型也均预测出降水偏少的形势，其Ps评分在67.4~74.2分之间。对这4种预测方法进行回归集成，得到的预测结果与实况最为接近，其Ps评分在77.2分，可以看出，回归集成较其他单一预测模型在空间分布和量级的预测上较单一预测模型更优。

3 前冬海温对广东汛期降水的影响及其与序列方法的集成

虽然降水序列本身包括了很多重要信息，但降水本身只是一个事后信息，更有效的提高短期气候预测的方法是分析影响降水的物理系统，由于影响降水系统的复杂性，这种信息具有非线性和非平稳性。众所周知，降水的成因很复杂，因而降水预测是目前短期气候预测的难点和重点。降水不仅受自身变化规律的影响，同时受到外强迫和大气环流影响。随着全球气候变暖变“乱”，仅用降水时间序列本身预测一方面不稳定，另一方面预测不出异常等级。因此，有必要考虑对降水预测具有指示意义的外强迫信号和环流因子。然而，考虑到环流因子是一个相对的快变量，很容易遗忘前期信号对降水的指示，另一方面大气的混沌性会限制季节尺度的预报性。因此，下面开展海温外强迫因子与降水自身规律结合构建预测系统。

将广东86站汛期降水量进行EOF展开，取能表述其平均特征的第一特征向量对应的时间系数与前期不同时期全球海温(SST)计算相关，结果得到前冬(12月到次年2月)赤道东太平洋地区有一正高相关中心(图略)，对该区域海温序列进行EMD展开，取前3个IMF分量作为预测备选因子构建逐步回归方程。对2002—2011年海温模型进行回报检验(表 4)，近10年平均Ps和同号率分别为68.3分和52.8%，与降水单预测模型结果相当。进一步将海温因子耦合到回归集成预测模型，其Ps评分结果与纯降水集成模型相当，但同号率评分略高3.1%。海温因子对降水的可能影响：当冬季赤道东太平洋海温偏高，有利西太平洋副热带高压偏南，易出现南方类雨型(陈兴芳等，2003)。

4 结论和讨论

本文引入能够将非线性、非平稳过程的数据进行线性化和平稳化处理的EMD方法，对广东降水和影响降水的海温因子的时间序列进行时间尺度分离，从复杂的非平稳信号提取出相对简单的不同时间尺度振荡的准周期信号，选取能较好描述降水周期特征的关键备选因子，然后以均生回归、均生相关、韵律拟合误差和拟合误差4种方法构建集成预测模型。结果得到：

(1) EMD方法能提取降水序列不同尺度的周期特征，广东汛期降水主要呈现为4、7、12和25 a周期，其中以4 a周期为主，占总方差贡献的63.0%，其次是25 a长周期，它和4 a短周期占方差贡献的79%，与原序列相关高达0.88，4和25 a周期的重构值基本能包含汛期降水的绝大部分信息。

(2) 采用均生相关、均生回归、韵律拟合误差法和拟合误差预测方法对近10年广东汛期进行回报，结果得到各单一预测模型的Ps评分的平均分为68~73分，同号率评分的平均分为50%~58%，而回归集成Ps评分和同号率的平均值分别达到79.8分和68.8%，较单一预测模型的评分分别偏高了10分和10%以上。同时，回归集成也较好地模拟出降水的偏多空间分布型。从而开展物理模型的集成预测，能有效提高短期气候预测水平。

(3) 将具有降水指示信号的前冬赤道东太平洋海温因子耦合到回归集成预测模型，其Ps评分结果与纯降水集成模型相当，但同号率评分略高3.1%。可见，寻找对降水预测具有指示意义的外强迫信号和环流因子可一定程度上提高降水预报的准确率。

本文采用EMD方法提取能较好描述降水周期特征的关键备选因子，并分别采用均生回归、均生相关、韵律拟合误差和拟合误差4种方法构建预测模型，接着采用回归方法对4种模型进行集成，研究得到引入EMD和回归集成方法能有效提高短期气候预测效果。同时，将具有降水指示信号的前冬赤道东太平洋海温因子耦合到回归集成预测模型，其Ps评分结果与纯降水集成模型相当，但同号率评分略高3.1%。寻找对降水预测具有指示意义的外强迫信号和环流因子可一定程度上提高降水预报的准确率。但是由于影响降水因子的复杂性，且外强迫因子和环流因子均是和降水序列作前期相关来寻找关键区，而这种相关关系并不十分稳定，且这种信息易受非线性作用的干扰，因而如何提取影响降水系统中可识别的具有可预报性的物理因子，是今后将进一步深入开展的工作。