2. 中国科学院对地观测与数字地球科学中心, 北京 100094;
3. 上海大学空间遥感与空间信息科学研究中心,上海 200072
2. Center for Earth Observation and Digtial Earth of CAS, Beijing 100094;
3. Research Center of Remote Sensing and Spatial Information Scicnce, Shanghai University, Shanghai 200072
在全球变化的大背景下,部分地区的极端气候事件如干旱等发生的频率和强度增加(Dai et al, 2004;马柱国, 2005;陶诗言等,2009);且旱灾影响范围广、造成的经济损失严重。因此,干旱的综合评估和监测对研究气候变化以及防灾减灾均具有重要的现实意义(姚凤梅等,2007;李德等,2011;林纾,2010)。为研究干旱发生、发展规律, 学者们对干旱指标进行了大量研究(侯英雨等,2007;侯威等,2012;谢五三等,2011)。Palmer(1965)综合考虑了前期降水、水分供给、水分需求、实际蒸散量、潜在蒸散量等要素,以水分平衡为基础而建立了一个气象干旱指数(Palmer Drought Severity Index,PDSI);该指数被广泛应用于各个国家的干旱评估、旱情比较以及对旱情的时空分布特征的分析中。McKee等(1993;1995)提出了基于降水量的标准化降水指标(Standardized Precipitation Index,SPI),通过研究降水量的统计分布规律反映干旱的强度和持续时间。以上的干旱指数主要侧重于反映气象干旱,而农业干旱(土壤或植被的水分亏损)的影响亦不可低估。随着遥感技术的发展应用,另一类基于卫星遥感信息的干旱监测方法(张佳华等,2007;侯英雨等,2010;王开存等,2003)开始兴起,如基于植被指数的干旱监测指数,基于地表温度的干旱监测指数,以及植被指数和地表温度相结合的干旱监测指数(Kogan, 1995)等。Idso等(1981)根据热量平衡原理通过计算整个冠层覆盖的实际蒸散与潜在蒸散量的比值,提出了作物水分胁迫指数(Crop Water Stress Index,CWSI)来研究灌溉地区的水分胁迫。
由于全球增暖, 升温引起蒸发潜力的变化对地表湿润状况产生了重要影响。马柱国等(2001)定义月降水量与月最大潜在蒸发的比值为地表湿润指数,并以此分析了中国北方干旱区的地表干湿分布状况。张庆云(1999)根据华北地区的气候特点,采用高桥浩一郎公式计算陆面蒸发,仅从气象角度通过降水与蒸发之差揭示了华北干旱化的特征及对水资源的影响。实际蒸散是由土壤蒸发与植物蒸腾两部分组成的,它是土壤—植被—大气系统中能量、水分传输和转换的重要过程(Priestley et al, 1972; Mu et al, 2007)。土壤含水量的变化和蒸发等过程, 直接影响着干旱的发生、发展和消亡, 因此基于蒸散的干旱指数具有清晰的物理含义(张元元,2011)。研究表明,蒸散发可以很好地反映土壤和植被干旱状况,是许多干旱指标中重要的水分支出项之一, 所以准确地测定和估算蒸散量是干旱指标能否精确反映干旱程度的关键(袁文平等,2004)。传统的单点蒸散估算方法有:波文比—能量平衡法、涡动相关法(Kaimal et al, 1994),Penman-Monteith法(Penman, 1948; Monteith, 1963)等。这些方法都是基于单个点的观测,空间代表性较差,对于大面积的非均匀的地表蒸散估算存在一定的误差。目前区域蒸散的估算方法主要有:基于水量平衡原理的水文气象学方法和基于能量平衡原理的遥感蒸散模型。Su(2000;2002)利用卫星的可见光、近红外和热红外波段资料,结合气象数据,提出了根据表面能量平衡原理估算地表相对蒸散的SEBS模型(占车生等,2010)。土壤—植被—大气传输(SVAT)模型(Sellers et al, 1996)通过模拟辐射传输、湍流输送、水热传导及植被的光合作用等一系列物理和生理过程,估算区域的水热通量(包括蒸散)及相关的地表参数(Olioso et al, 2005)。然而,这些模型都比较复杂,需要的参数众多且不易获得,这对模型的应用存在一定的局限性。Wang等(2008)发展了一种基于地表净辐射,植被指数,温度以及土壤湿度的简单的估测实际蒸散ET的半经验统计方法。该蒸散模型已在代表不同地表覆盖类型(包括草地、森林、农田等,水体除外)的美国大陆的12个站点和全球的20个站点上得到了很好的验证(Wang et al, 2007; Yao et al, 2010; 2011),且模拟结果与GSWP-2估算的ET值接近一致。这个ET模型综合考虑了大气、植被和土壤等因素,最大的优点是所需的气象参数较少且容易获取,并且由于遥感数据的使用而大大提高了空间分辨率。
本文以华北地区为研究区域, 首先利用地表实测数据验证这一蒸散模型的模拟效果,然后分析实际蒸散的时空分布特征及其影响参数,最后应用基于实际蒸散ET模型和潜在蒸散PET的蒸散干旱指数EDI研究华北干旱分布特点,并与其他干旱指数做对比,进而为大面积的干旱监测和评估提供一定的依据。
1 资料和方法 1.1 数据资料与处理 1.1.1 模型输入数据本文所研究的华北地区经纬度范围为:33°~43°N、108°~120°E。使用的网格点资料有: (1) 辐射资料:GEWEX-SRB (Global Energy and Water Cycle Experiment-Surface Radiation Budget), 即全球能量与水分循环试验的地表辐射收支工程的卫星反演辐射产品。辐射通量包括大气层顶和地面的向上、向下短波和长波辐射通量,水平分辨率分别为1° ×1°。(2) NDVI资料:1 km空间分辨率的MODIS NDVI 16天合成产品,即MOD13A2。华北地区每次共有6景影像才能完全覆盖,经过拼接、重投影、感兴趣区域的提取得到华北地区所需的NDVI数据。(3) 气温资料:欧洲中期数值预报中心(ECMWF)最新版本的再分析资料ERA-Interim中2 m高度上的日平均气温和日最高、最低气温,经纬度分辨率为0.75°。将以上资料统一插值到0.25°×0.25°网格点上,华北地区共有49×41=2009个网格点。
1.1.2 地面验证数据(1) 实际蒸散量的验证站点位于中国科学院栾城农业生态系统试验站,地理位置为37°53′N、114°41′E,海拔50.1 m,所在区域属于半干旱半湿润暖温带季风气候。栾城站地带植被类型为落叶阔叶林,主要种植制度为冬小麦—玉米两熟。随着涡动相关技术在水汽通量和能量传输等方面的广泛应用,其可靠性也逐步被认可(张建君,2009),故本文采用2008年栾城站涡动相关法测量的实际日蒸散量作为对比验证。另外,利用平均气温、最高最低气温、日照时数、实际水汽压等日值资料作为计算栾城站地表净辐射的输入参数。
(2) 华北干旱分布的对比分析使用的站点资料有:在华北地区均匀的选取数据质量较好的84个站点的温度、降水量日值观测数据来计算PDSI指数和降水距平百分率,以此作为华北干旱的对比分析和辅助验证。
1.2 蒸散模型与参数求算 1.2.1 实际蒸散ET实际蒸散ET是水循环的关键一环,决定了土壤—植被—大气系统中的水、热传输。为了减少蒸散模型的输入参数,Wang(2007;2008) 发展了估算蒸散的半经验统计模型:
| $ \begin{array}{l} ET = {R_{\rm{n}}}\left[ {0.1440 + 0.6495NDVI + 0.0090{T_{\rm{a}}} - } \right.\\ \;\;\;\;\;\;\;\;\left. {0.0163\left({{T_{{\rm{max}}}} - {T_{{\rm{min}}}}} \right)} \right] \end{array} $ | (1) |
其中,Rn为地表净辐射(单位:W·m-2),NDVI为归一化植被指数,Ta为每日平均气温,Tmax和Tmin分别为每日最高和最低气温,ET为实际蒸散通量或潜热通量(单位:W·m-2)。因为土壤湿度对蒸散有潜在的重要影响,该ET模型通过考虑每日的地表温度变化或每日的气温变化的不同,将土壤湿度的影响包含到ET的参数化中。将实际蒸散通量ET转换为日实际蒸散量Edaily(单位:mm·d-1), 则有:
| $ {E_{{\rm{daily}}}} = \frac{{86400 \times ET}}{\lambda } $ | (2) |
式中,Edaily为每日实际蒸散量, λ为水的汽化潜热(单位:J·kg-1),可由下式求得:
| $ \lambda = \left({2.501 - 0.002361 \times {T_{\rm{a}}}} \right) \times {10^6} $ | (3) |
其中,Ta为日平均气温。
1.2.2 潜在蒸散PET潜在蒸散PET表示在一定气象条件下水分供应不受限制时, 某一固定下垫面可能达到的最大蒸发蒸腾量。这里采用Hargreaves公式(Hargreaves, 1989)估测潜在蒸散, 则有:
| $ PET = 0.0023{R_{\rm{a}}}\left({{T_{{\rm{mean}}}} + 17.8} \right)\sqrt {{T_{{\rm{max}}}} - {T_{{\rm{min}}}}} $ | (4) |
式中,Ra为大气顶太阳辐射(单位:W·m-2), Tmax和Tmin分别为每日最高和最低气温, Tmean为每日平均气温,且Tmean=(Tmax+Tmin)/2。PET为潜在蒸散通量。将潜在蒸散通量PET转化为日潜在蒸散量Ep daily, 则有:
| $ {E_{p\;{\rm{daily}}}} = \frac{{86400 \times PET}}{\lambda } $ | (5) |
式中,Ep daily为每日潜在蒸散发量, λ为水的汽化潜热,可由式(3) 求得。
1.2.3 地表净辐射Rn地表净辐射Rn是地面能量、物质输送与交换过程的原动力, 是气候形成及气候变化的主要因素(何延波等,2006)。地表净辐射(Rn)可表示为:
| $ {R_{\rm{n}}} = {R_S} \downarrow - {R_S} \uparrow + {R_L} \downarrow - {R_L} \uparrow $ | (6) |
式中,RS↓和RS↑分别为地表向下和向上的短波辐射, RL↓和RL↑分别为地表向下和向上的长波辐射。
采用FAO推荐用于计算参考作物蒸散量的Penman-Monteith公式中的估算净辐射的方法(刘新安,2006)估算栾城站的地表净辐射,并以此作为实际蒸散模型的输入参数。如下式所示:
| $ {R_{\rm{n}}} = {R_{{\rm{ns}}}} - {R_{{\rm{nl}}}} $ | (7) |
| $ {R_{{\rm{ns}}}} = \left({1 - \alpha } \right)\left({a + bn/N} \right){R_{\rm{a}}} $ | (8) |
| $ \begin{array}{l} {R_{{\rm{nl}}}} = 2.45 \times {10^{ - 9}}\left({0.1 + 0.9\frac{n}{N}} \right)\left({0.34 - } \right.\\ \;\;\;\;\;\;\;\;\left. {0.14\sqrt {ed} } \right)\left({T_{kx}^4 + T_{kn}^4} \right) \end{array} $ | (9) |
其中,Rns和Rnl分别为净短波辐射和净长波辐射(单位:MJ·m-2·d-1);Ra为天文辐射(单位:MJ·m-2·d-1);α为反照率,取0.23;a和b取公式中推荐的参数, 即:a=0.25, b=0.5;n和N分别为实际日照时数和最大天文日照时数(单位:h);ed为实际水汽压(单位:kPa);Tkx和Tkn分别为最高绝对温度和最低绝对温度(单位:K)。
1.3 蒸散干旱指数EDI蒸散干旱指数EDI根据Anderson等提出的蒸散胁迫指数ESI的机理(Anderson et al, 2007),给出蒸散干旱指数EDI的表达式,即:
| $ EDI = 1 - \frac{{ET}}{{PET}} $ | (10) |
其中,ET和PET分别由式(1) 和式(4) 得到。理论上,EDI的量值在0~1之间。土壤表面的干旱越严重,水分胁迫就越严重,则潜在蒸散与实际蒸散的差值越大,即EDI值越高。反之,土壤越湿润,EDI值越低。
为了突出某年、季、月或旬的EDI指数与多年相应的平均值的差异,我们引入的EDI距平指数,可表示为:
| $ \Delta EDI\left(i \right){\rm{ = }}EDI\left(i \right) - \frac{1}{n}\sum\limits_{i = 1}^n {EDI\left(i \right)} $ | (11) |
式中,i为年份。
2 结果与分析 2.1 蒸散模拟值与实测值的相关分析本文将实际蒸散ET模型的模拟值与华北地区的栾城站实测的蒸散值作对比分析。图 1a和1b分别为栾城站2008年模拟ET日值与实测ET日值的对比图以及模拟ET值与实测ET值对应的时间变化图。
|
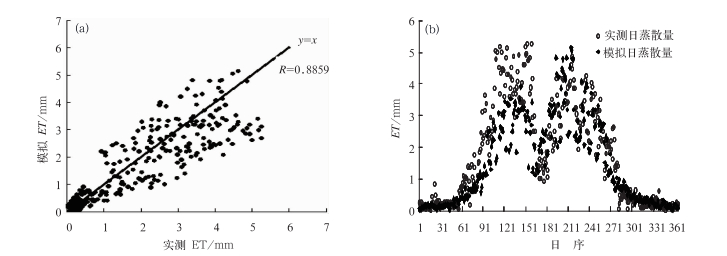
图 1 栾城站2008年日蒸散模拟值与测量值的散点图(a)及二者的日序变化图(b) Fig. 1 Scatterplots of estimated daily ET and measured ET (a) and time series of daily estimated ET and measured ET (b) at Luancheng Site in 2008 |
如图 1a所示,通过与涡动相关法测量的蒸散值对比,可以发现蒸散模拟值与实测值较为接近,且相关系数为0.8859, 均方根误差为0.75 mm。模拟的蒸散量与实测值的平均偏差为-0.22 mm,这表明总体上模拟值小于实测值,而且由图 1b可以看出,在春季(3—5月)蒸散模拟值基本小于测量值,但其他月份蒸散值与测量值则较为接近;这是由于半干旱地区在春季容易受到近地层水平平流输送的影响,涡动相关法的测量值比实际蒸散值偏高(张强等,2011)。此外,图 1b总体显示出模拟值与实测值有着较为一致的随季节变化的趋势,且模拟值和实测值均在6月份(日序数151~181之间)有一个较窄的波谷,这是由于此时小麦收获,而玉米则刚刚播种,因此植被蒸散量出现一个低值区。以上分析说明本模型对农田蒸散发具有很好的模拟能力。
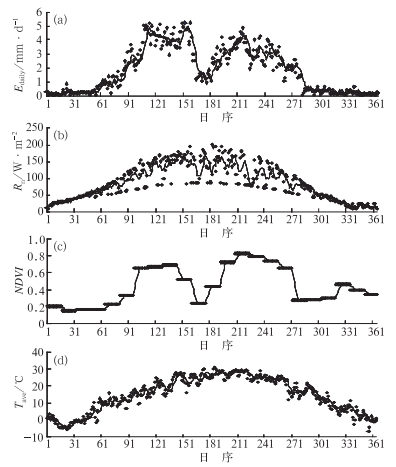
2.2 实测蒸散量与各影响因子的时间变化分析为了检验蒸散模型中各参数能否反映影响实际蒸散量的主要因子,这里进一步分析了实际蒸散与各参数的关系。图 2给出了2008年栾城站实测日蒸散量与日地表净辐射、植被指数和日平均温度的时间变化趋势图。由该图可以看出,实测日蒸散量与各影响因子存在着明显的季节性变化,总体上在夏季达到最大值,冬季为最小值;6月份ET和NDVI的低谷值则是由于受到了作物收获的影响。此外,实测日蒸散量与各影响参数的总体变化趋势较为一致,其中,实际蒸散量与地表净辐射以及NDVI的相关性较好。这表明了该蒸散模型能够抓住影响实际蒸散的主要因素,从而可以较为准确地估算实际蒸散量。
|
图 2 2008年栾城站每日实际蒸散观测值(a)、地表净辐射(b)、植被指数(c)和平均气温(d)的时间变化图 (黑实线为各参数7天滑动平均趋势线) Fig. 2 Time series of daily measured ET (a), surface net radiation (b), vegetation index (c) and average air temperature (d) (Blank solid line denotes 7 d moving average of each parameter) |
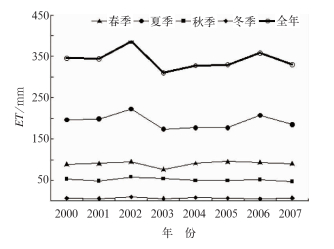
图 3给出了华北地区2000—2007年各季节及全年的实际蒸散量变化。由该图可知,各季节的实际蒸散量由大到小分别为:夏季>春季>秋季>冬季;且秋季和冬季的实际蒸散年际变化不大,全年实际蒸散量的变化趋势与夏季实际蒸散量的变化趋势最为一致;因此华北地区年蒸散量的大小及变化趋势主要由夏季蒸散量所决定。
|
图 3 华北地区2000—2007年各季节及全年的实际蒸散量变化图 Fig. 3 Variation of actual evapotranspiration in North China for each season and whole year during 2000-2007 |
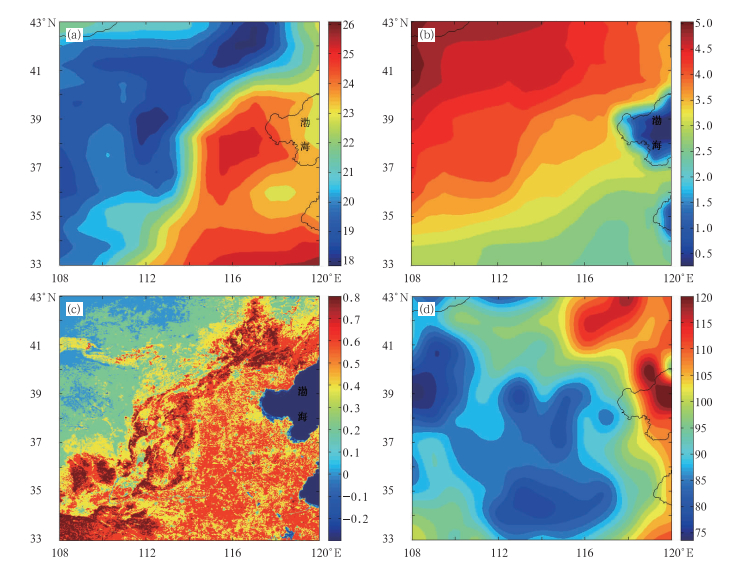
图 4给出了华北地区2007年夏季平均的日地表净辐射、植被指数、平均气温以及日最高气温和最低气温的差值的空间分布。由图 4a可以看出:华北地区的平均气温呈东南—西北走向,即由东南向西北延伸,平均气温越来越低,高温区和低温区基本以45°角的斜线为分界线。由图 4b可以看出,华北地区的温差基本上也是呈东南—西北走向,不同的是,越往西北延伸,温差越来越大;比较图 4a和4b可以发现温差的空间分布趋势与平均气温的空间分布趋势基本相反,即平均温度越低的地区温差越大,反之则越小。如图 4c所示,华北的西北部地区的NDVI值较低,这是由于该地区岩石或裸土较多,植被覆盖较少且长势较差;而南部地区的NDVI值较高,表明该地区植被覆盖较多且长势较好;深蓝色区域为渤海、黄海部分海域,NDVI呈现为负值。由图 4d可以看出,地表净辐射的高值区位于华北的东北部地区,低值区位于华北的西部和中南部地区。
|
图 4 华北地区2007年夏季的日平均气温(a)、温差(b)、植被指数(c)和地表净辐射(d)的空间分布图 Fig. 4 Spatial distributions of daily mean temperature (a), temperature difference (b), vegetation index (c) and surface net radiation (d) in North China during the summer of 2007 |
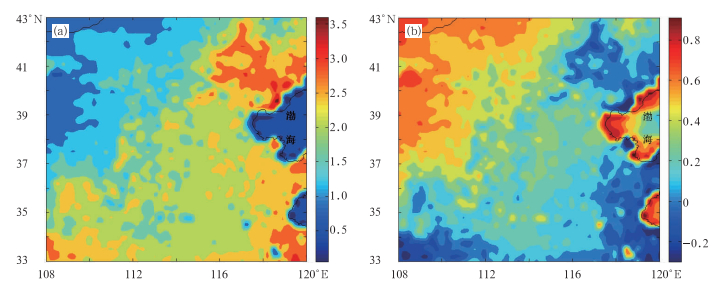
图 5给出了华北地区2007年夏季平均的实际蒸散量和蒸散干旱指数的空间分布。由图 5a可以看出,华北地区实际蒸散量由东南向西北方向降低,这与图 4c中的植被指数分布特点较为一致,即植被长势越好,蒸腾越大;由于实际蒸散包括植被蒸腾和土壤蒸发两部分,故实际蒸散另一部分取决于土壤蒸发,而土壤蒸发又与土壤含水量或土壤湿度有关,本文的ET模型通过考虑日温差的大小,将土壤湿度的影响包含到ET的参数化中,即温差越大表明土壤湿度越小,因此图 4b反映出华北地区的土壤湿度由东南向西北减少,这与图 5a中反映的华北西北部的实际蒸散比东南部小的分布特点是一致的。此外,实际蒸散的东北部的高值中心和西北部的低值中心与图 4d中的地表净辐射的高低值中心基本对应,这说明二者的相关性较好。由图 5b可知,华北地区的EDI值由东南向西北方向增加,这与蒸散量的空间分布规律基本相反,二者呈现出明显的反位相;虽然EDI值还与潜在蒸散量有关,但对于半干旱地区,植被受水分胁迫较重,实际蒸散量越低,在很大程度上反映了该地区越是干旱,即EDI值越高。
|
图 5 华北地区2007年夏季的平均日实际蒸散ET(a)和蒸散干旱指数EDI(b)的空间分布 Fig. 5 Spatial distributions of actual mean evapotranspiration (a) and evapotranspiration drought index (b) in North China during the summer of 2007 |
多年EDI平均值能反映出相应时段的平均干湿程度,但不能代表某一地区的异常干湿状况,因此我们引入EDI距平值(ΔEDI)来反映某地发生干旱的严重程度。以华北地区2007年夏季发生的干旱情况为例,利用6—8月的ΔEDI值的空间分布的变化来反映这次旱情的演变过程,并与由PDSI指数和降水距平百分率所指示的干旱做对比。
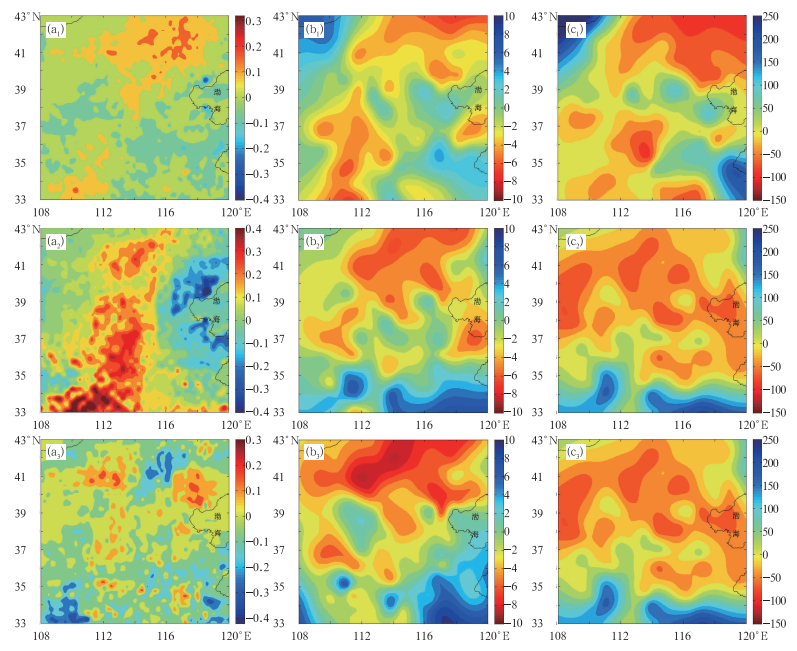
图 6给出了华北地区2007年6—8月的ΔEDI指数和PDSI指数以及降水距平百分率的空间分布。由ΔEDI指数各月的空间分布来看,6月华北的北部偏东地区以及南部偏西的少部分地区出现中等干旱,东南部地区较湿润;与PDSI指数和降水距平百分率所显示的干旱空间分布特征基本一致,不同的是降水距平百分率所指示的干旱程度和湿润程度较重,PDSI指数次之,这是由于降水距平百分率只有降水量一个因素决定,对降水较为敏感;而ΔEDI指数则是综合了地表净辐射、植被指数、平均气温和温差这些要素,同时包含了土壤和植被作用的干旱指标,因此ΔEDI指数比单一的气象因子更能准确地表征干旱特征。到7月,ΔEDI指数显示华北地区的旱情向南部蔓延并且干旱程度加重,东部地区相对湿润;PDSI指数和降水距平百分率也显示出华北北部发生干旱的面积扩大且旱情加重,但西南部的旱情明显减轻且比较湿润,这主要受到了当月降水的影响;而ΔEDI指数所反映的华北西南部的旱情严重是因为上个月这个地区的降水偏少对作物生长和土壤湿度的影响累积。8月,ΔEDI指数显示华北地区的旱情开始减轻,尤其是南部地区,说明上个月的该地较多的降水使得旱情明显减轻,华北北部大部分为轻微干旱,只有河北北部和内蒙古中部地区有中等干旱发生。PDSI指数和降水距平百分率所显示的干湿空间分布趋势与之较为相似,只是干旱程度偏重。
|
图 6 华北地区2007年6—8月的EDI距平指数(a)、PDSI指数(b)以及降水距平百分率(c)的空间分布 (a1, b1, c1) 6月,(a2, b2, c2) 7月,(a3, b3, c3) 8月 Fig. 6 Spatial distribution of EDI anomaly (a), PDSI (b) and percentage of precipitation anomaly (c) in North China from June to August 2007 (a1, b1, c1) June, (a2, b2, c2) July, (a3, b3, c3) August |
由上述分析可知,ΔEDI指数与在对旱情的指示和干旱程度的判定上是比较准确和可靠的。与PDSI指数和降水距平百分率相比,ΔEDI指数还考虑了辐射的影响以及作物和植被对土壤湿度和辐射的反馈作用;PDSI指数和降水距平百分率主要反映气象干旱且对干旱的判定偏重,而ΔEDI指数主要反映农业干旱因此反映的旱情滞后于前者。此外,ΔEDI指数所反映干旱分布的空间分辨率明显高于PDSI指数和降水距平百分率的,这是由于站点降水资料的空间分辨率较低。
3 结论通过蒸散模拟值与实测值的对比验证以及ΔEDI指数与PDSI指数和降水距平百分率在华北的对比应用,有如下结论:
(1) ET模型估测的蒸散值与实测值的相关性很好,其模拟精度对于大面积干旱监测的空间尺度上是可用的。
(2) 实测蒸散量与各影响因子的时间变化趋势较为一致,且存在明显的季节性变化;其中,实际蒸散量与地表净辐射以及NDVI的相关性最好。
(3) 华北地区实际蒸散量由东南向西北方向降低,与EDI指数的空间分布特征基本相反,这是因为半干旱地区受水分胁迫较重,实际蒸散量越低在很大程度上反映了该地区越是干旱,即EDI值越高。
(4) ΔEDI指数除了包含大气干旱,还综合了土壤和植被等对大气干旱的反馈作用,因此判定干旱程度的准确度较好,而且该指数在反映干旱分布的空间分辨率上明显高于PDSI指数和降水距平百分率。
致谢:感谢沈彦俊老师提供2008年栾城站涡动相关法测量的实际蒸散数据。
何延波, SuZhongbo, JiaLi, 等, 2006. SEBS模型在黄淮海地区地表能量通量估算中的应用[J]. 高原气象, 25(6): 1092-1110. |
侯英雨, 何延波, 柳钦火, 等, 2007. 干旱监测指数研究[J]. 生态学杂志, 26(6): 892-897. |
侯英雨, 张佳华, 延昊, 等, 2010. 利用卫星遥感资料估算区域尺度空气温度[J]. 气象, 36(40): 75-79. |
侯威, 张存杰, 高歌, 2012. 基于气候系统内在层次性的气象干旱指数研究[J]. 气象, 38(6): 701-711. DOI:10.7519/j.issn.1000-0526.2012.06.008 |
李德, 杨太明, 张学贤, 等, 2011. 2008—2009年宿州秋冬低温干旱成因分析与影响评估[J]. 气象, 37(5): 615-621. DOI:10.7519/j.issn.1000-0526.2011.05.014 |
林纾, 张东方, 王永光, 等, 2010. MOS方法在西北地区东部春季干旱预警中的应用与检验[J]. 气象, 36(5): 98-101. DOI:10.7519/j.issn.1000-0526.2010.05.014 |
刘新安, 于贵瑞, 何洪林, 等, 2006. 中国地表净辐射推算方法的研究[J]. 自然资源学报, 21(1): 139-145. DOI:10.11849/zrzyxb.2006.01.018 |
马柱国, 2005. 中国北方干湿演变规律及其与区域增暖的可能联系[J]. 地球物理学报, 48(5): 1011-1018. |
马柱国, 符淙斌, 2001. 中国北方干旱区地表湿润状况的趋势分析[J]. 气象学报, 59(6): 737-746. DOI:10.11676/qxxb2001.077 |
陶诗言, 卫捷, 孙建华, 等, 2009. 2008/2009年秋冬季我国东部严重干旱分析[J]. 气象, 35(4): 3-10. DOI:10.7519/j.issn.1000-0526.2009.04.001 |
王开存, 陈长和, 郭铌, 2003. 用NOAA/AVHRR探测地表反射率和NDVI的订正及误差分析[J]. 应用气象学报, 14(2): 165-175. |
谢五三, 田红, 2011. 五种干旱指标在安徽省应用研究[J]. 气象, 37(4): 503-507. DOI:10.7519/j.issn.1000-0526.2011.04.016 |
姚凤梅, 张佳华, 孙白妮, 等, 2007. 气候变化对中国南方稻区水稻产量影响的模拟和分析[J]. 气候与环境研究, 12(5): 659-666. |
袁文平, 周广胜, 2004. 干旱指标的理论分析与研究展望[J]. 地球科学进展, 19(6): 982-991. |
占车生, 夏军, 2010. 中国陆面蒸散发量的遥感反演及时空格局[M]. 北京: 知识产权出版社, 37-78.
|
张佳华, 郭文娟, 姚凤梅, 2007. 植被水分遥感监测模型的研究[J]. 应用基础与工程科学学报, 15(1): 45-53. |
张建君, 2009. 农田日蒸散量估算方法研究[M]. 北京: 中国农业科学院, 2-8.
|
张强, 张之贤, 何晓梅, 等, 2011. 陆面蒸散量观测方法比较分析及其影响因素研究[J]. 地球科学进展, 26(5): 538-547. |
张庆云, 1999. 1880年以来华北降水及水资源的变化[J]. 高原气象, 18(4): 486-495. |
张元元, 2011. 应用FY-2地表蒸散产品监测西南特大干旱[J]. 气象, 37(8): 999-1005. DOI:10.7519/j.issn.1000-0526.2011.08.012 |
Anderson M C, Norman J M, Mecikalski J R, et al, 2007. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 2. Surface moisture climatology[J]. J Geophys Res, 112: D11112. DOI:10.1029/2006JD007507 |
Dai A G, Trenberth K T, Qian T T, 2004. A global dataset of Palmer drought severity index for 1870-2002: Relationship with soil moisture and effects of surface warming[J]. J Hydrometeorol, 5: 1117-1130. DOI:10.1175/JHM-386.1 |
Hargreaves G H, 1989. Accuracy of estimated reference crop evapotranspiration[J]. J Irrig Drain Eng, 115: 1000-1007. DOI:10.1061/(ASCE)0733-9437(1989)115:6(1000) |
Idso S B, Jackson R D, Pinter P J, 1981. Measuring yield reducing plant water potential depressions in wheat by infrared thermometry[J]. Irrig Sci, (2): 205-212. |
Kaimal J C, Finnigan J J, 1994. Atmospheric Boundary Layer Flows[M].
Oxford: Oxford University Press, 289.
|
Kogan F N, 1995. Application of vegetation index and brightness temperature for drought detection[J]. Adv Space Research, 15: 91-100. |
McKee T B, Doesken N J, Kleist J. 1993. The relationship of drought frequency and duration to time scales. Preprints, Eighth Conf. on Applied Climatology, Anaheim, CA, Amer Meteor Soc, 179-184.
|
McKee T B, Doeskin N J, Kleist J. 1995. Drought monitoring with multiple time scales. Preprints, Ninth Conf on Applied Climatology, Dallas, TX, Amer Meteor Soc, 233-236.
|
Monteith J L, 1963. Environmental Control of Plant Growth[M].
New York: Academic Press, 95-112.
|
Mu Qiaozhen, Heinsch F A, Zhao Maosheng, et al, 2007. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data[J]. Remote Sensing of Environment, 111: 519-536. DOI:10.1016/j.rse.2007.04.015 |
Olioso A, Inoue Y, Ortega-farias S, et al, 2005. Future directions for advanced evapotranspiration modeling: Assimilation of remote sensing data into crop simulation models and SVAT models[J]. Irrigation and Drainage Systems, 19(3-4): 377-412. DOI:10.1007/s10795-005-8143-z |
Palmer W C, 1965. Meteorological drought US[J]. Weather Bureau Research Paper, 45: 58. |
Penman H L, 1948. Natural evaporation from open water, bare soil land and grass[J]. Proceedings of the Royal Society of London (Series A), 193: 120-146. DOI:10.1098/rspa.1948.0037 |
Priestley C H B, Taylor R J, 1972. On the assessment of surface heat flux and evaporation using large-scale parameters[J]. Mon Wea Rev, 100: 81-92. DOI:10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2 |
Sellers P J, Los S O, Tucker C J, et al, 1996. A revised Land Surface Parameterization (SiB2) for atmospheric GCMS. Part Ⅱ:The generation of global fields of Terrestrial Biophysical Parameters from satellite data.[J]. J Climate, 9(4): 706-737. DOI:10.1175/1520-0442(1996)009<0706:ARLSPF>2.0.CO;2 |
Su Z, 2000. Remote sensing of land use and vegetation for mesoscale hydro logical studies[J]. International Journal of Remote Sensing, (2): 213-233. |
Su Z, 2002. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes[J]. Hydrology and Earth System Sciences, (6): 86-100. |
Wang K, Liang S, 2008. An improved method for estimating global evapotranspiration based on satellite determination of surface net radiation, vegetation index, temperature, and soil moisture[J]. J Hydrometeor, 9: 712-727. DOI:10.1175/2007JHM911.1 |
Wang K, Wang P, Li Z, et al, 2007. A simple method to estimate actual evapotranspiration from a combination of net radiation, vegetation index, and temperature[J]. J Geophys Res, 112: D15107. DOI:10.1029/2006JD008351 |
Yao Y, Liang S, Qin Q M, et al, 2010. Monitoring Drought over the Conterminous United States Using MODIS and NCEP Reanalysis-2 Data[J]. J App Meteor Climatol, 49(8): 1665-1680. DOI:10.1175/2010JAMC2328.1 |
Yao Y, Liang S, Qin Q M, et al, 2011. Satellite detection of increases in global land surface evapotranspiration during 1984-2007[J]. International Journal of Digital Earth, 5(4): 299-318. |
 2013, Vol. 39
2013, Vol. 39 
