2. 南京信息工程大学,南京 210044
2. Nanjing University of Information Science and Technology, Nanjing 210044
零度层亮带是指雪花或冰晶降落到零度层附近,表面发生融化而使雷达反射率突然增大的现象(Austin et al, 1950),它是影响雷达资料质量的一个非常重要的因素,尤其对气象和水文中的雷达定量估测降水有重要的影响(Huggel et al, 1996),它会引起近处到中等距离零度层亮带附近降水的高估(Bellon et al, 2005)和远处零度层亮带以上冰晶、雪花的低估(Smith, 1986)。除了对降水估测的影响外,零度层亮带的识别还有助于降水类型的预报(Kain et al, 2000),探测到亮带说明降水性质已经从对流云逐渐转化为层状云连续性降水(张培昌等, 2001)。此外,零度层亮带的高度可以确定潜在的冰层区域,对航空(亮带的出现表明大气中不存在强烈的对流和湍流活动)和数值预报的资料同化有用(Zhang et al, 2008)。同时,利用雷达回波追踪、识别和外推法来进行临近预报的工作,也会受到零度层亮带的干扰,影响预报结果。因此,自动识别零度层亮带的高度、区域,并对亮带进行订正具有非常重要的意义。
目前,国内外已经开展了很多用反射率垂直廓线(vertical profile of reflectivity,VPR)识别和订正零度层亮带的方法,这些方法大致分为气候VPR法、平均体扫VPR法和局地VPR法(Zhang et al, 2010)。这些VPR研究方法有其各自的优缺点。气候VPR由某个空间区域内的长时间雷达观测资料平均获得。这些VPR不能代表降水垂直结构的时空变化。通常在得不到实时和小尺度VPR的情况下作为缺省VPR使用。平均体扫VPR通常是由一个或几个体扫的多个仰角获得(Germann et al, 2002)。这些VPR比起气候的VPR可以更好地捕获降水垂直结构的时间变化,尤其在业务中得到广泛应用。平均体扫VPR通常假设在一个雷达覆盖区有相同的结构,而忽略了降水垂直廓线的空间变化。Andrieu等(1995)提出了一种复杂的方法滤除雷达取样的影响(波束加宽作为距离的函数)并用两个仰角反演出平均VPR。这种方法后来被(Vignal et al, 1999)用于多个仰角在20 km×20 km的小区域内反演局地VPR, 其估测结果比平均体扫法在雷达估测降水中有更大改进,但由于计算量太大而不利于业务应用(Vignal et al, 2000)。
国内也做了一些零度层亮带识别和订正的研究(邵玲玲等,2004;史锐等,2005;孙晓光等,2011;王德旺等,2012;黄钰等,2013)。张乐坚等(2010)提出一种使用S波段天气雷达回波三维特征和反射率因子垂直廓线来识别零度层亮带的方法(3DVPR-BBID),但并未对零度层亮带的订正方法进行研究。陈明轩等(2006)利用插值到直角坐标系中的雷达反射率因子(CAPPI)资料识别亮带,用亮带上和亮带下的反射率因子值对亮带中的反射率因子值进行插值修正,以消除亮带。肖艳姣等(2010)提出一种自动识别零度层亮带平均高度、厚度和区域以及对亮带进行抑制的算法。
但以上这些对亮带识别和订正的工作都是在平原地区进行的,雷达覆盖情况较好,没有严重的遮挡问题,而且对亮带订正效果的检验也只是通过对比亮带订正前后的雷达反射率CAPPI和反射率垂直廓线,而没有将亮带的订正用于雷达估测效果中,用其对降水估测的改善检验亮带订正的效果。青藏高原平均海拔在4500 m以上,其独特的地理环境,对我国东南部、东亚地区乃至全球的天气气候都有重大影响(徐祥德等, 2006)。在即将开展的第三次青藏高原大气科学试验中,天气雷达是地面综合观测中非常重要的手段,对于认识青藏高原云和降水过程在水分和能量循环中的作用有重要意义(Liu et al, 2002)。然而青藏高原海拔高,零度层低,遮挡严重,零度层亮带是影响雷达资料质量的最重要的因素之一,尤其是在雷达定量估测降水中,亮带以下的降水范围非常有限,未经过亮带订正的反射率导致降水的显著高估。因此对零度层亮带进行识别订正,对减小由于零度层亮带高估引起的降水估测误差,提高青藏高原复杂地形下的雷达估测降水精度有重要意义。
1 资料来源雷达资料采用西宁新一代C波段天气雷达观测的原始体扫数据,西宁雷达位于(36.5978°N、101.7750°E),海拔高度2445 m,扫描方式是VCP21,扫描9个仰角(0.5°、1.5°、2.4°、3.4°、4.3°、6.0°、9.9°、14.5°、19.5°),反射率的距离库的分辨率是0.25 km,方位分辨率约为1°。雷达资料的时间采用世界时。
探空资料采用西宁探空站(36.71°N、101.75°E)的温度廓线资料,将其垂直线性内插得到0℃的高度。探空资料的时间为北京时,时间分辨率为12 h,即北京时间08和20时有资料,探空零度层高度单位为km。
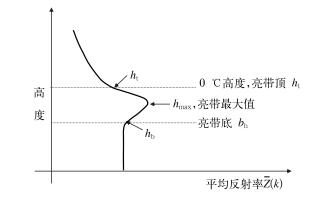
2 零度层亮带的识别及订正方法 2.1 零度层亮带的识别方法青藏高原地形复杂,雷达波束受到严重的地形遮挡,雷达最低几层仰角常会探测到地物回波。如果不对地物回波进行识别,就会导致平均反射率垂直廓线及亮带识别参数的较大误差,影响亮度层的亮带识别及订正。因此,在对零度层亮带进行识别订正前,要对雷达体扫资料进行地物回波的识别(庄薇等,2012)。零度层亮带的反射率垂直廓线的概念模型如图 1所示,平均反射率最大值Zmax的高度hmax在零度层高度(亮带顶ht)以下的几百米内,沿着平均反射率最大值Zmax向上(到亮带顶ht)或向下(到亮带底hb),平均反射率值Z(k)都会减小。
|
图 1 反射率垂直廓线零度层亮带概念模型 Fig. 1 Schematic illustration of conceptual model of bright band layer in vertical profile of reflectivity |
零度层亮带的识别方法如下:
(1) 同一高度上的平均反射率Z(k)的计算
根据反射率库的高度,每一层的高度定义如下:
| $ h\left(k \right) = k \times \Delta h\;\;\;\;k = 2, N $ | (1) |
式中,k是层的序号,Δh为100 m,N为层数,本文中N的最大值取150。
平均反射率Z(k)定义如下:
| $ \bar Z\left(k \right) = \frac{1}{M}\sum\limits_{elv = 1}^{{N_{elv}}} {\sum\limits_{i = 1}^{{N_a}} {\sum\limits_{j = 81}^{320} {Z\left({j, i, elv} \right)} } }, \;\;\;k = 2, N $ | (2) |
式中,Z(k)是第k层的平均反射率(单位:dBz),Z(j, i, elv)是第k层内反射率大于某一阈值threshold1(在本文中threshold1取10 dBz)的反射率值, M是第k层内反射率大于threshold1的个数。Nelv是仰角层数,Na是径向数,在这里,计算平均反射率Z(k)的数据采用整个体扫9层仰角(Nelv=9)360个径向(Na=360) 上距离雷达20~80 km(库长为0.25 km, 因此对应第81到320个库)范围内的所有库。
(2) 亮带的识别
首先找出平均反射率最大值Zmax所在高度hmax,然后分别向上和向下找出最大反射率递减某一阈值threshold2(在本文中threshold2取10%)的高度ht和hb,如果同时满足式(3)~式(6) 这4个条件,则零度层亮带存在:
| $ {h_{\rm{t}}} - {h_{\rm{b}}} \ge {D_1} $ | (3) |
| $ {h_{\rm{t}}} - {h_{\max }} \le {D_2} $ | (4) |
| $ {h_{\max }} - {h_{\rm{b}}} \le {D_2} $ | (5) |
| $ {h_{\rm{t}}} - {h_{\rm{b}}} \le {D_3} $ | (6) |
参考Zhang等(2008)和张乐坚等(2010)对亮带深度和对称性约束参数的取值及对西宁雷达观测到的13次层状云降水过程的分析,得出D1=400 m,D2=1000 m,D3=1500 m。
2.2 零度层亮带的订正方法用上述方法对雷达资料进行零度层亮带的识别,对于识别出亮带的雷达资料,需要对亮带进行有效订正,以减小其对雷达估测降水的影响。
订正方法如下:
(1) 平均反射率Z(k, elv)的计算
首先计算出每层仰角所有方位的平均反射率Z(k, elv),计算公式如下:
| $ \bar Z\left({k, elv} \right) = \frac{1}{M}\sum\limits_{i = 1}^{{N_a}} {\sum\limits_{j = 1}^{{N_g}} {Z\left({j, i, elv} \right), \;\;\;k = 2, N} } $ | (7) |
式中,Z(k, elv)是第elv层仰角在第k层内所有方位的平均反射率(单位:dBz),Z(j, i, elv)是第k层内反射率大于某一阈值threshold1的反射率值, M是第k层内反射率大于threshold1的个数。在这里计算平均反射率Z(k, elv)的数据采用第elv层仰角,360个径向(Na=360),所有库(Ng是库数,Ng=1000) 上的数据。
式(7) 与式(2) 的差别在于:识别算法中计算的平均反射率Z(k)是用整个雷达体扫9层仰角的数据计算的,而订正算法中的平均反射率Z(k, elv)是仅用第elv层仰角的数据计算的。这样在订正算法中,对于每一层仰角,都可以计算出该仰角的反射率垂直廓线。
(2) 零度层亮带顶ht(elv)和亮带底hb(elv)的确定
每层仰角中最大的平均反射率Zmax所在的高度hmax(elv),然后分别向上和向下找出最大反射率递减某一阈值threshold2的高度ht(elv)和hb(elv)。
(3) 零度层亮带顶斜率α和亮带底斜率β的计算
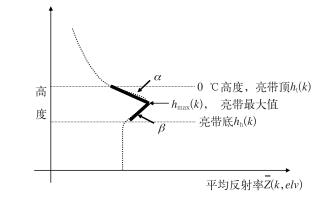
α是亮带顶ht(elv)到亮带最大值所在高度hmax(elv)之间用最小二乘法拟合的斜率,β是亮带底hb(elv)到亮带最大值所在高度hmax(elv)之间用最小二乘法拟合的斜率。当零度层亮带存在时,α总是负值,而β总是正值。当零度层亮带接近地面时,α=β。图 2是反射率垂直廓线及各参数的示意图。
|
图 2 反射率垂直廓亮带及文中5个参数的示意图 Fig. 2 Vertical profile of reflectivity and five parameters in the text |
(4) 反射率订正值dBz(j, i, elv)的求取
由图 2可知,反射率订正值dBz(j, i, elv)的计算公式如下:
| $ dBz\left({j, i, elv} \right) = \left\{ \begin{array}{l} \frac{{\left[ {h\left({j, i, elv} \right) - {h_{\max }}\left({elv} \right)} \right]}}{\alpha } + \\ \frac{{\left[ {{h_{\max }}\left({elv} \right) - {h_b}\left({elv} \right)} \right]}}{\beta }, \\ h\left({j, i, elv} \right) > {h_{\max }}\left({elv} \right);\\ \frac{{\left[ {h\left({j, i, elv} \right) - {h_b}\left({elv} \right)} \right]}}{\beta }, \\ h\left({j, i, elv} \right) \le {h_{\max }}\left({elv} \right) \end{array} \right. $ | (8) |
| $ dBZ\left({j, i, elv} \right) = dB{Z_0}\left({j, i, elv} \right) - dBz\left({j, i, elv} \right) $ | (9) |
其中dBZ0(j, i, elv)为雷达观测的反射率,dBZ(j, i, elv)为订正后的反射率。同时需要满足以下3个条件时才进行订正:(1) 受遮挡的方位不超过30%的仰角层;(2) 由于本文只考虑零度层亮带对降水高度的影响,暂不考虑零度层以上冰晶、降雪的影响,因此,只有当反射率订正值dBz(j, i, elv)大于0时,才进行订正;(3) 由于零度层亮带可能是不均匀的,因此只在亮带区才进行订正[当雷达观测值dBZ0(j, i, elv)大于同高度上的平均反射率Z(height(j, i, elv), elv)时,为亮带区],非亮带区不进行订正。
对于受遮挡的方位超过30%的仰角层,其上层被识别为遮挡的区域,下层对应的反射率用上一层仰角的反射率订正值dBz(j, i, elv+1) 订正。上层未被识别为遮挡的区域,下层对应的反射率不进行订正。
3 个例分析 3.1 亮带高度与零度层高度的对比用西宁探空站的温度廓线进行垂直线性内插得到零度层的高度,并与探空资料时间相近的用雷达资料得到的零度层亮带高度进行比较,表 1列出了个例的结果(探空资料和雷达资料的时间均为世界时)。
|
|
表 1 雷达识别的亮带底、亮带顶、亮带峰值高度和探空得到的0℃层高度(单位:km) Table 1 The bright band bottom, top, peak reflectivity heights identified by the Xining radar and 0℃ height from Xining sounding site (unit: km) |
对比雷达时间与探空时间较为接近的资料(表 1),雷达探测到的零度层亮带顶的高度与探空观测的0℃层高度较为接近,雷达探测到的零度层亮带高度比用探空资料得到的0℃层高度低几百米,这与亮带通常位于0℃层等温线以下几百米的经典结论基本一致。但在某些个例中,亮带高度与0℃层所在高度非常接近,甚至与0℃层所在高度重合。
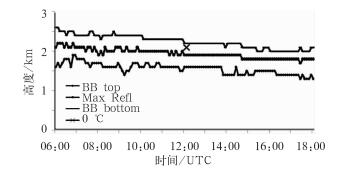
图 3为2009年7月25日西宁雷达识别的亮带底、亮带顶、亮带峰值高度和西宁探空站温度廓线插值得到的0℃层高度的时间序列图。从2009年7月25日00:00到7月26日00:00 3次探空资料的0℃层高度分别是2.4、2.2和1.9 km,0℃层高度随时间降低。7月25日06:00到7月25日18:00,雷达识别的亮带底、亮带顶和亮带峰值高度也是随时间降低的。探空资料插值的0℃层高度和雷达识别的亮带高度的变化趋势一致。
|
图 3 2009年7月25日西宁雷达识别零度层亮带的亮带底(BB bottom)、亮带顶(BB top)、亮带峰值(Max Refl)高度和西宁探空站的温度廓线进行垂直线性内插得到0℃层高度 Fig. 3 Time series of the bright band bottom, top, peak reflectivity heights identified by Xining radar and 0℃ height from Xining sounding site on 25 July 2009 |
对于7月25日12:00左右的雷达探测到的零度层亮带顶的高度与探空观测的0℃层高度较为接近,雷达探测到的零度层亮带峰值高度比用探空资料得到的0℃层高度低几百米。亮带顶和亮带底的平均高度差大约为1 km,也就是说亮带的厚度大约在1 km左右,这满足亮带识别的条件亮带顶与亮带底的高度差在1500 m以内(见式6)。
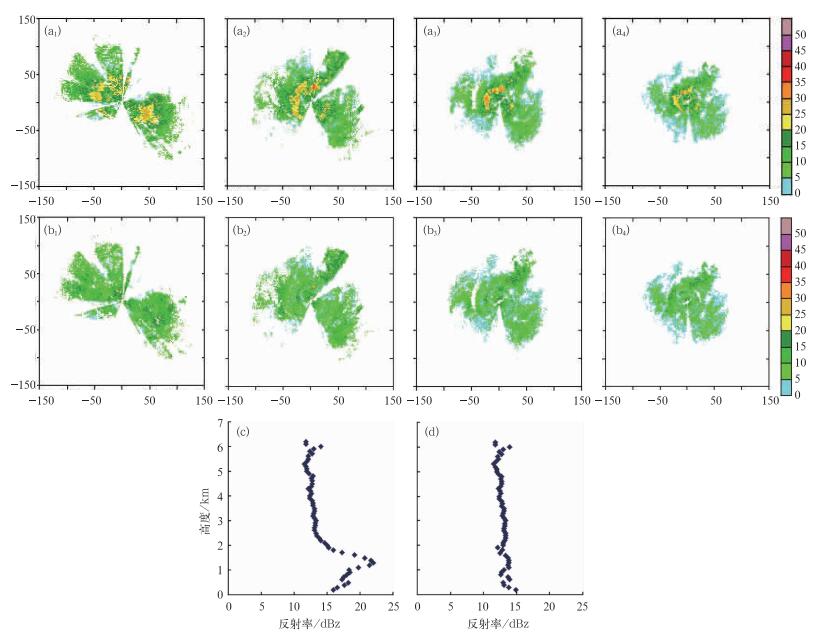
3.2 亮带带订正前后对比分析图 4是2010年5月25日12:03西宁雷达第二~五层(1.5°、2.4°、3.4°、4.3°)仰角的亮带订正前(a1~a4)后(b1~b4)的反射率PPI图。图 4c是2010年5月25日12:03西宁雷达的反射率垂直廓线。根据反射率垂直廓线(图 4c)可以判断出零度层亮带的高度以及在各层仰角PPI图上的位置。对比各层仰角订正前后的反射率PPI图,亮带区的高反射率已经被订正,非亮带区的反射率基本没有变化。图 4d是亮带订正后的反射率垂直廓线,从图中可以看出,亮带订正前的反射率垂直廓线在零度层高度附近有显著弯曲,亮带订正后,显著弯曲消失。
|
图 4 2010年5月25日12:03西宁雷达第二~五层(1.5°、2.4°、3.4°、4.3°)仰角的亮带订正前(a1~a4)后(b1~b4)的反射率PPI图,亮带订正前(c)后(d)的反射率垂直廓线 Fig. 4 Reflectivity on the second tilt to the fifth tilt before (a1-a4) and after (b1-b4) the bright band correction, vertical profile of reflectivity before (c) and after (d) bright band correction from Xining radar at 12:03 UTC 25 May 2010 |
2009年7月26日西宁雷达观测到一次大范围层状云降水(图 5),根据反射率垂直廓线(图 5c)可以判断出零度层高度在2 km左右,反射率在零度层附近有突然的增大(图 5a),反射率垂直廓线有显著的弯曲(图 5c)。订正后,亮带区的高反射率因子值得到订正(5b),反射率垂直廓线的显著弯曲消失(5d)。
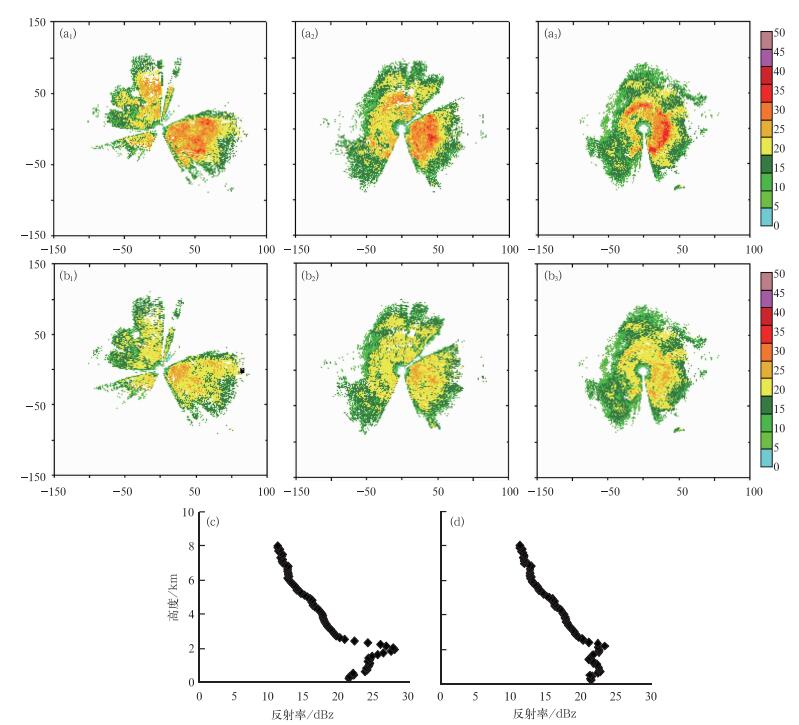
|
图 5 2009年7月25日12:04西宁雷达第二~四层(1.5°、2.4°、3.4°)仰角的亮带订正前(a1~a3)后(b1~b3)的反射率PPI图,亮带订正前(c)后(d)的反射率垂直廓线 Fig. 5 Reflectivity on the second tilt to the forth tilt before (a1-a3) and after (b1-b3) the bright band correction, vertical profile of reflectivity before (c) and after (d) bright band correction from Xining radar at 12:04 UTC 25 July 2009 |
图 6是2010年5月25日12:03西宁雷达亮带订正前后的混合扫描反射率,混合扫描反射率计算方法采用气候统计法(Zhuang,2012)。比较亮带订正前后的混合扫描反射率,亮带订正后的反射率变得平滑,亮带区的高反射率值得到了有效订正。
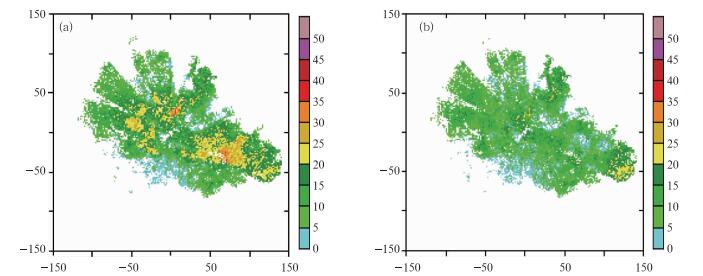
|
图 6 2010年5月25日12:03西宁雷达亮带订正前(a)后(b)的混合扫描反射率 Fig. 6 Hybrid scan reflectivity before (a) and after (b) bright band correction from Xining radar at 12:03 UTC 25 May 2010 |
2009年8月2日06:01西宁雷达观测到一次强降水过程,亮带订正前后的混合扫描反射率如图 7。雷达西部有很强的降水回波,在零度层附近,有厚度在2 km以上的亮带,亮带订正后,亮带区的高反射率得到了有效订正,非亮带区则基本没有变化。
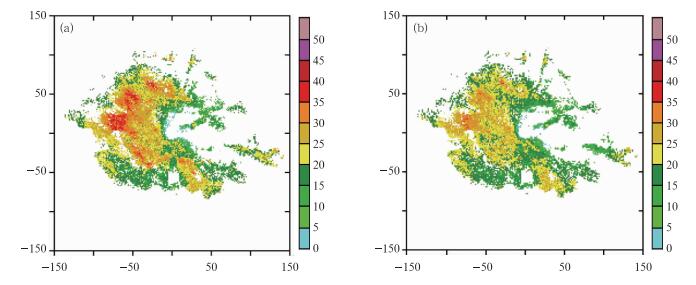
|
图 7 2009年8月2日06:01西宁雷达亮带订正前(a)后(b)的混合扫描反射率 Fig. 7 Hybrid scan reflectivity before (a) and after (b) bright band correction from Xining radar at 06:01 UTC 2 August 2009 |
2010年5月20日12:04西宁雷达探测到一次较弱的降水过程,亮带订正前后的混合扫描反射率如图 8。本次层状云降水过程中的亮带不十分明显,厚度不到1 km,在进行亮带订正后,亮带区的高反射率被订正,非亮带区则基本没有变化。
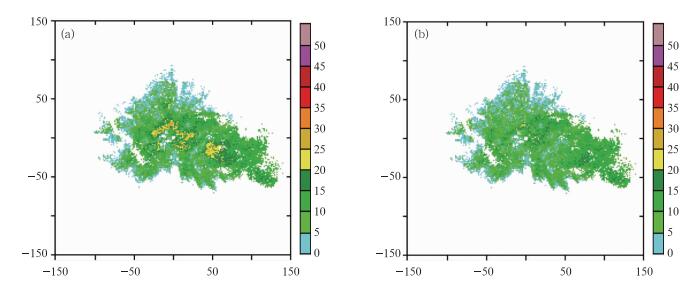
|
图 8 2010年5月20日12:04西宁雷达亮带订正前(a)后(b)的混合扫描反射率 Fig. 8 Hybrid scan reflectivity before (a) and after (b) bright band correction from Xining radar at 12:04 UTC 20 May 2010 |
从以上这几个个例的分析可知,无论是对强降水过程还是弱降水过程,亮带区都得到了有效订正,而对非亮带区则基本没有影响。亮带订正后的混合扫描反射率将用于雷达估测降水。
4 亮带订正在降水估测中的应用在本文的研究中,用Z-R关系将混合扫描反射率转化成降水率,再用雷达累计降水与自动站雨量计观测的地表降水进行比较。图 9是2009年8月2日在亮带订正前(图 9a)后(图 9b)雷达估测降水与雨量计观测降水的散点图。其中雨量站为西宁雷达覆盖范围内的20个雨量站,雨量为2009年8月2日的降水过程7 h的降雨量。从图可以看出亮带订正前,雷达估测的降水明显高估,亮带订正后,雷达的高估得到有效订正,与雨量计的观测值较为一致。
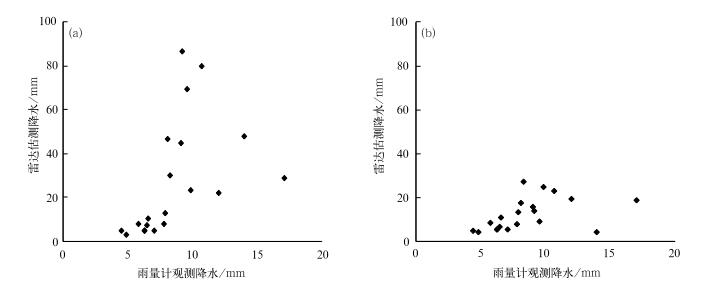
|
图 9 2009年8月2日亮带订正前(a)后(b)雷达估测降水和雨量计观测降水散点图 Fig. 9 Scattered plots of radar precipitation estimate before (a) and after (b) bright band correction vs gauge observation from Xining radar on 2 August 2009 |
为了进一步评估亮带订正效果,本文用雷达雨量计比值(BIAS)、均方根误差(RMSE)、相对平均绝对误差(RMAE)和相对平均偏差(RMB)4个量计算雷达估测降水误差,计算公式如下:
| $ BIAS = \frac{{\sum\limits_{i = 1}^n {{R_i}} }}{{\sum\limits_{i = 1}^n {{G_i}} }} $ | (10) |
| $ RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left({{R_i} - {G_i}} \right)}^2}} } $ | (11) |
| $ RMAE = \frac{{\frac{1}{n}\sum\limits_{i = 1}^n {\left| {{R_i} - {G_i}} \right|} }}{{\frac{1}{n}\sum\limits_{i = 1}^n {{G_i}} }} $ | (12) |
| $ RMB = \frac{{\frac{1}{n}\sum\limits_{i = 1}^n {\left({{R_i} - {G_i}} \right)} }}{{\frac{1}{n}\sum\limits_{i = 1}^n {{G_i}} }} $ | (13) |
这里Ri和Gi分别代表第i个配对的雷达估测的降水和雨量计观测的降水。配对的雨量计和雷达反射率需要满足雷达估测的降水Ri和雨量计观测的降水Gi都大于0。
表 2是2009年8月2日亮带订正前后雷达估测降水和雨量计观测值BIAS、RMSE、RMAE、RMB对比。从表中可以看出,亮带订正后的BIAS、RMSE、RMAE、RMB明显比亮带订正前的小,亮带订正减小了雷达估测降水的误差。
|
|
表 2 2009年8月2日亮带订正前后雷达降水估测BIAS、RMSE、RMAE、RMB对比 Table 2 The BIAS, RMSE, RMAE, RMB for radar precipitation estimate before and after bright band correction |
青藏高原海拔高、零度层低,零度层以下的降水范围非常有限,不得不用零度层亮带区的资料估测降水,从而造成降水的过高估计。本文利用雷达反射率垂直廓线,研究识别亮带的参数及亮带存在的条件,并在此基础上研究了亮带的订正方法,得出以下结论:
(1) 利用整个体扫的平均反射率垂直廓线及识别亮带的参数,在经过大量个例验证的基础上,得出亮带存在的条件。并将探空温度廓线垂直线性内插得到的零度层高度与探空相近时刻雷达识别出的亮带高度进行了对比。青藏高原的零度层高度很低,雷达识别出的亮带高度在探空资料零度层高度以下几百米,但在部分个例中,亮带高度与零度层高度非常接近,甚至重合。
(2) 利用每一层仰角的反射率垂直廓线及订正参数对亮带区域进行了订正,亮带区的高反射率值被订正,非亮带区基本不受影响。反射率垂直廓线在零度层附近有显著弯曲,亮带订正后,反射率垂直廓线的显著弯曲消失。
(3) 用亮带订正前的反射率估测的降水,雷达估测的降水明显偏高。用亮带订正后的反射率估测的降水与雨量计观测的降水比较一致,减小了零度层亮带引起的降水的高估。通过对亮带订正前后雷达雨量计比值(BIAS)、均方根误差(RMSE)、相对平均绝对误差(RMAE)和相对平均偏差(RMB)的分析表明,亮带订正后的雷达估测降水误差显著减小。
陈明轩, 高峰, 2006. 利用一种自动识别算法移除天气雷达反射率因子中的亮带[J]. 应用气象学报, 17(2): 207-214. DOI:10.11898/1001-7313.20060212 |
黄钰, 马建立, 阮征, 等, 2013. 2010年夏季北京零度层亮带特征统计[J]. 气象, 39(6): 704-709. DOI:10.7519/j.issn.1000-0526.2013.06.006 |
邵玲玲, 黄炎, 2004. WSR-88D雷达降水产品的优化[J]. 气象, 30(5): 24-29. DOI:10.7519/j.issn.1000-0526.2004.05.006 |
史锐, 程明虎, 崔哲虎, 等, 2005. 多普勒雷达实时反射率因子垂直廓线观测研究[J]. 气象, 31(9): 39-43. DOI:10.7519/j.issn.1000-0526.2005.09.008 |
孙晓光, 刘宪勋, 贺宏兵, 等, 2011. 毫米波测云雷达融化层自动识别技术[J]. 气象, 37(6): 720-726. DOI:10.7519/j.issn.1000-0526.2011.06.010 |
肖艳姣, 刘黎平, 李中华, 等, 2010. 雷达反射率因子数据中的亮带自动识别和抑制[J]. 高原气象, 29(1): 197-205. |
王德旺, 刘黎平, 仲凌志, 等, 2012. 毫米波雷达资料融化层亮带特征的分析及识别[J]. 气象, 38(6): 712-721. DOI:10.7519/j.issn.1000-0526.2012.06.009 |
徐祥德, 陈联寿, 2006. 青藏高原大气科学试验研究进展[J]. 应用气象学报, 17(6): 756-772. DOI:10.11898/1001-7313.20060613 |
张乐坚, 程明虎, 陶岚, 2010. CINRAD-SA/SB零度层亮带识别方法[J]. 应用气象学报, 21(2): 171-179. DOI:10.11898/1001-7313.20100206 |
张培昌, 杜秉玉, 戴铁丕, 2001. 雷达气象学[M]. 北京: 气象出版社, 306.
|
庄薇, 刘黎平, 余燕群, 等, 2012. 雷达地物回波模糊逻辑识别法的改进及效果检验[J]. 气象学报, 70(3): 576-584. DOI:10.11676/qxxb2012.047 |
Andrieu H, Creutin J D, 1995. Identification of vertical profiles of radar reflectivity for hydrological applications using an inverse method. Part Ⅰ: Formulation[J]. J Appl Meteor, 34: 225-239. DOI:10.1175/1520-0450(1995)034<0225:IOVPOR>2.0.CO;2 |
Austin P M, Bemis A C, 1950. A quantitative study of the "bright band" in radar precipitation echoes[J]. J Meteor, 7: 145-151. DOI:10.1175/1520-0469(1950)007<0145:AQSOTB>2.0.CO;2 |
Bellon A, Lee G W, Zawadzki I, 2005. Error statistics of VPR corrections in stratiform precipitation[J]. J Appl Meteor, 44: 998-1015. DOI:10.1175/JAM2253.1 |
Germann U, Joss J, 2002. Mesobeta profiles to extrapolate radar precipitation measurements above the Alps to ground level[J]. J Appl Meteor, 41: 542-557. DOI:10.1175/1520-0450(2002)041<0542:MPTERP>2.0.CO;2 |
Huggel A, Schmid W, Waldvogel A, 1996. Raindrop size distributions and the radar bright band[J]. J Appl Meteor, 35: 1688-1701. DOI:10.1175/1520-0450(1996)035<1688:RSDATR>2.0.CO;2 |
Kain J S, Goss S M, Baldwin M E, et al, 2000. The melting effects as a factor in precipitation-type forecasting[J]. Wea Forecasting, 15: 700-714. DOI:10.1175/1520-0434(2000)015<0700:TMEAAF>2.0.CO;2 |
Liu Liping, Feng Jinming, Chu Rongzhong, 2002. The diurnal variation of precipitation in monsoon season in the Tibetan Plateau[J]. Adv Atmos Sci, 19(2): 365-378. DOI:10.1007/s00376-002-0028-6 |
Smith C J, 1986. The reduction of errors caused by bright bands in quantitative rainfall measurements made using radar[J]. J Atmos Oceanic Technol, 3: 129-141. DOI:10.1175/1520-0426(1986)003<0129:TROECB>2.0.CO;2 |
Vignal B, Andrieu H, Creutin J D, 1999. Identification of vertical profiles of reflectivity from volume-scan radar data[J]. J Appl Meteor, 38: 1214-1228. DOI:10.1175/1520-0450(1999)038<1214:IOVPOR>2.0.CO;2 |
Vignal B, Galli G, Joss J, et al, 2000. Three methods to determine profiles of reflectivity from volumetric radar data to correct precipitation estimates[J]. J Appl Meteor, 39: 1715-1726. DOI:10.1175/1520-0450-39.10.1715 |
Zhang J, Langston C, Howard K, 2008. Brightband identification based on vertical profiles of reflectivity from the WSR-88D[J]. J Atmos Oceanic Technol, 25(10): 1859-1872. DOI:10.1175/2008JTECHA1039.1 |
Zhang J, You Q C, 2010. A real-time algorithm for the correction of brightband effects in radar-derived QPE[J]. J Hydrometeorology: 1157-1171. |
Zhuang Wei, Liu Liping, 2012. A reflectivity climatology algorithm for hybrid scans and its application to radar coverage over the Tibetan Plateau[J]. Acta Meteor Sinica, 26(6): 746-757. DOI:10.1007/s13351-012-0606-1 |
 2013, Vol. 39
2013, Vol. 39 