短时强降水往往诱发中小河流洪水、山洪、滑坡和泥石流等灾害(张家国等,2010;李向红等,2010;曲晓波等,2010;慕建利等,2012;樊建勇等,2012)。天气雷达联合地面雨量计估测降水,可以获得高分辨率的降水分布,是进行强降水监测的重要手段(Smith et al,1996;Baeck et al,1998;张利平等,2007;刘晓阳等,2010)。同时,精细化的定量降水估测产品也是水文模型的重要输入资料,对洪峰预测最敏感的因素就是流域降水量的空间变化(彭涛等,2010;赵琳娜等,2012)。
平均校准法是常用的天气雷达联合地面雨量计估测降水方法(Wilson et al,1979;Fulton et al,1998),要求研究区域内的雨量计达到一定数量时才进行校准,校准前需要将天气雷达反射率因子按照考虑某种滴谱分布的Z-I关系将反射率因子反演为雨强(Marshall et al,1948;Willis et al, 1989),其中Z(单位:mm6·m-3)为反射率因子,I(单位:mm·h-1)为雨强。平均校准法有两个方面的误差需要特别加以考虑:一方面,如果在天气雷达覆盖范围内采用统一的校准因子,由于不同风暴之间微物理和动力方面的差异,雷达覆盖范围内的平均偏差就不能代表具体的风暴单体,导致某些区域校准后的雨量与地面雨量计测值相比偏高过大,同时另一些区域偏低严重(Bauer-Messmer et al,1997;Fulton,1999)。随着地面雨量计密度的增加,雷达覆盖范围内的校准向范围逐渐减小的局地校准发展(McEnery et al,2005;张亚萍等,2007;李建通等,2009;田付友等,2010;Kitzmiller et al,2011)。另一方面,将天气雷达反射率因子转换为降水率估测需要考虑滴谱分布,而滴谱分布在不同强度的降水中差别很大(Willis et al,1989)。汪瑛等(2011)提出了雷达定量降水动态分级Z-I关系估算方法,改进了对短时强降水的估测效果。为了在局地范围内得到更为精确的强降水监测结果,张亚萍等(2013)提出了天气雷达联合地面雨量计估测降水的局地分级平均校准方法,个例分析表明,局地分级平均校准方法对强降水的估测效果优于局地平均校准方法。本文利用天气雷达联合地面雨量计定量降水估测的局地平均校准法和局地分级平均校准法,进行2012年7月21日20:00—22日01:00(北京时,下同)重庆市荣昌县及附近的降水分布估计,并对方法中的局地校准半径的选取进行讨论。同时,在进行降水分布估计的基础上,对荣昌县吴家镇双流村的洪水与降水和河网分布的关系进行分析,为今后进行中小河流洪水的气象风险预报提供参考。
1 天气形势配置与降水实况7月20日20:00至22日08:00,高原低槽东移影响四川盆地,但低槽前部的副热带高压(以下简称副高)东退缓慢,其环流控制长江中下游地区,高原低槽东移受阻,移速缓慢。21日20:00(图 1b),低槽前部四川盆地内中低层有西南涡生成,在阻塞形势下受低层偏北风的推动缓慢向东南方向移动,影响重庆西部;同时,贝加尔湖冷涡势力强大,冷涡底部冷空气在旋转槽的引导下南下,冷锋与西南涡共同影响,在副高的阻塞作用下形成重庆西部局部地区的大暴雨天气。
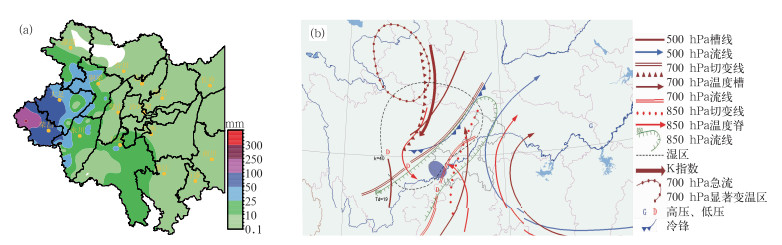
|
图 1 (a)重庆市西部2012年7月21日20:00至22日02:00雨量分布图, (b) 2012年7月21日20:00综合图 Fig. 1 (a) Rainfall distribution in the west of Chongqing from 20:00 BT 21 to 02:00 BT 22 July 2012, (b) synthetic synoptic chart at 20:00 BT 21 July 2012 |
7月21日傍晚开始,重庆市大部地区陆续出现了一次雷雨天气,西部部分地区、东北部局部地区及东南部局部地区出现了暴雨或大暴雨,其余大部地区小到中雨,局部大雨。7月21日20:00至22日02:00(图 1a),荣昌盘龙6 h累积雨量达253.2 mm,其中21日23:00盘龙小时雨量达180.9 mm。这次大暴雨天气导致荣昌县21个镇街出现洪涝灾害,5个城镇进水,受灾人口达16万,转移人口7千多,农作物受灾11万亩(1亩=661.7 m2),房屋垮塌1722间,山坪塘垮塌214口,渠道垮塌1136 m,损坏电力提灌站50处, 10座水库受损,公路垮塌42 km,地质滑坡175处,全县直接经济损失达2.04亿元。22日凌晨,由于清流河水暴涨,吴家镇双流村被淹没,积水最深达5 m。
2 天气雷达联合地面雨量计估测降水分布 2.1 降水估测方法图 2为天气雷达联合地面雨量计局地分级平均校准法估测降水流程图。
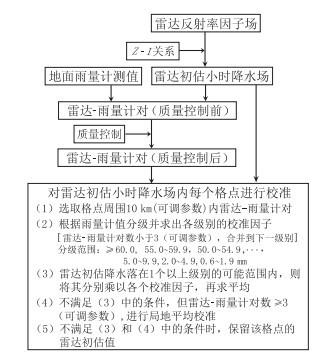
|
图 2 天气雷达联合地面雨量计局地分级平均校准法估测降水流程图 Fig. 2 Sketch flow chart for raingauge-based local classified average bias-adjusted algorithm for radar quantitative precipitation estimate |
在进行降水估测时,首先进行雷达-雨量计对的选取及质量控制。为了提取用于校准的雷达-雨量计对,需要得到雷达初估小时降水场。采用文献(Fulton et al,1998)中的Z=300I1.4关系生成每个时次的雷达估测瞬时雨强I,然后累积为小时降水,作为雷达初估值。对于每个雨量计,选取该雨量计上空及周围共9个格点(这里每个格点代表0.01°×0.01°)的雷达初估小时降水的平均值得到一个雷达-雨量计对。每个时次的雷达-雨量计对质量控制采用文献(Fulton et al,1998)中的方法,分为3步:第一步,去除雷达初估值或雨量计测值低于0.6 mm [可调参数,本文与文献(Fulton et al,1998)所用参数相同]的雷达-雨量计对,保证雷达和雨量计都测到降水;第二步,去除雷达初估值或雨量计测值高于200 mm[可调参数,文献(Fulton et al,1998)中所用参数为400 mm]的雷达-雨量计对;第三步,计算剩下的雷达-雨量计对的归一化绝对偏差,计算该绝对偏差数组的标准偏差Sd,若某雷达-雨量计对的归一化绝对偏差大于3Sd(可调参数),则去除该雷达-雨量计对,以减轻雷达初估值与雨量计测值偏差过大以及零度层亮带等的影响。
局地平均校准法是指对于雷达覆盖范围内的每个格点(本文每个格点代表0.01°×0.01°),选取其周围局地范围内一定数量雨量计进行平均校准。局地范围的半径为可调参数。局地区域内的平均校准因子F(Wilson et al,1979):
| $ F=\frac{\sum\limits_{i=1}^{N}{{{C}_{i}}}}{\sum\limits_{i=1}^{N}{{{R}_{i}}}} $ | (1) |
式中,N为用于校准的雨量计数,Ri和Gi为第i个雷达-雨量计对的雷达初估值和雨量计测值。将平均校准因子乘以雷达初估小时降水场,就得到平均校准后的雷达估测小时降水场。当至少有3个(可调参数)雷达-雨量计对的数据时才进行校准。
局地分级平均校准法是指在局地范围内选择一定数量雨量计进行分级平均校准。根据雨量计值所在的不同级别(60 mm以上为一个级别,以下分别按5 mm间隔一个级别,但5 mm以下时,分为2.0~4.9和0.6~1.9 mm两个级别),对雷达-雨量计对进行分组,然后分别按照式(1) 得到各级别的平均校准因子。当雨量计测值在较高级别范围内的雷达-雨量计对达不到3个(可调参数)时,合并到下一级别。各级别的上、下限除以该级别校准因子,可以得到相应的校准前雷达初估降水的可能范围。若某一格点的雷达初估降水落在几个级别的可能范围内,则将其乘以各个校准因子,然后求平均。若以上条件均不满足且雷达雨量计对达3个(可调参数)时,仍采用局地平均校准法,否则保留该格点的雷达初估值。
2.2 降水分布估计结果利用2012年7月21日20:00至22日01:00(北京时)的重庆CINRAD/SA雷达反射率因子(150 km范围)和MICAPS加密自动站(Automatic Weather Stations,AWS)雨量资料进行降水分布估计。荣昌及附近的雨量计密度约为55 km2一个雨量计。由于地形原因,重庆雷达西部0.5°仰角受到严重的波束遮挡,因此荣昌附近的雷达降水估测采用1.5°仰角反射率因子数据(就荣昌而言,距离重庆雷达最近的1.5°仰角回波高度约2.8 km,最远的约4.4 km)。为了尽量利用靠近地面的反射率因子数据,暂未考虑雷达锥面扫描造成的反射率因子不在同一水平面上造成的误差。
图 3为7月21日23:00经过质量控制后得到的雷达-雨量计对(黑色方块,110个,平均校准因子6.216) 和质量控制第3步中被去除的雷达-雨量计对(红色方块,4个,平均校准因子19.55)。从图 3可见,直接用Z-I关系得到的降水初估值对80 mm以上的强降水的低估非常严重,经过质量控制,80 mm·h-1以上的雷达雨量计对都被去除了。在质量控制第3步中去除雷达初估值与雨量计测值相差太大的点,在该时次反映为避免过大的平均校准因子导致对降水的高估,而不是指这些雨量计测值有质量问题。这里,质量控制第3步中被去除的4个雷达-雨量计对用于降水估测效果检验(简称检验站)。图 4给出不同方法得到的荣昌附近小时降水分布。图 4a为地面雨量计测量的降水分布,荣昌西部的一个雨量站观测到180.9 mm的小时降水。图 4b和4c为局地分级平均校准法反演结果,局地校准半径分别为10和15 km。图 4d为平均校准法反演结果(平均校准因子为6.216),图中还叠加了4个检验站测值。图 4e~4f为局地平均校准法反演结果,局地校准半径分别为10和15 km。由图 4可见,平均校准法(图 4d)对荣昌西部强降水的低估非常严重。经过局地较准后(图 4b、4c、4e和4f),对荣昌西部强降水的估计都有所提高。另外,图 4b~4f都在荣昌南部和四川泸州反演出一些强降水中心,与图 4a中区别较大,主要是由于雨量计未能完全监测到这些强降水中心。
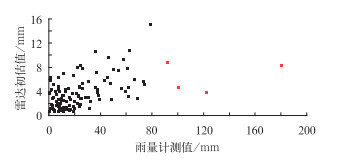
|
图 3 2012年7月21日23:00经过质量控制后得到的雷达-雨量计对(黑色方块)和质量控制第三步中被去除的雷达-雨量计对(红色方块) Fig. 3 Scatter plots of radar-rain gauge pairs after quality control (black) and discarded in step 3 of quality control (red) at 23:00 BT 21 July 2012 |
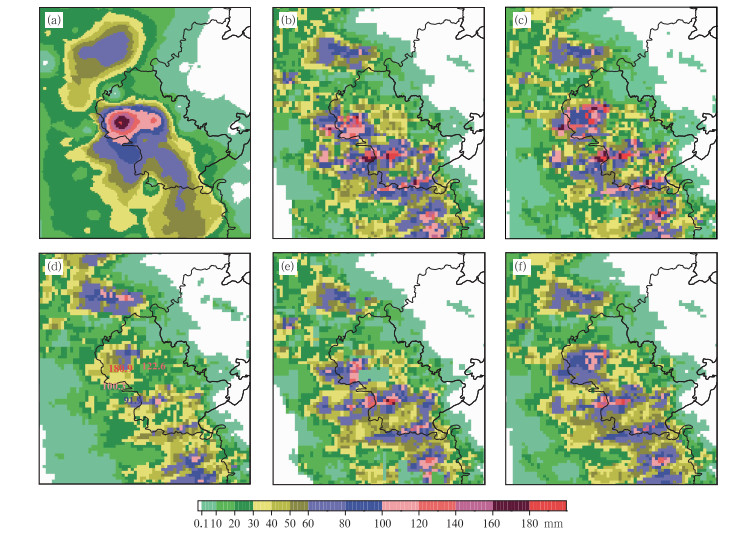
|
图 4 2012年7月21日23:00地面雨量计测量降水分布(a), 局地分级平均校准雷达估测降水分布(b~c), 平均校准雷达估测降水分布(d)和局地平均校准雷达估测降水分布(e~f) [其中(b)和(e)的局地校准半径为10 km,(c)和(f)的局地校准半径为15 km, (d)中叠加了用于检验的4个雨量计测值] Fig. 4 Rain gauge rainfall (a) and radar rainfall estimates (b-f) at 23:00 BT 21 July 2012 (b-c) obtained by local classified average bias-adjusted algorithm [local adjusted radius: (b) 10 km; (c) 15 km], (d) obtained by average bias-adjusted algorithm, (e, f) obtained by local average bias-adjusted algorithm [local adjusted radius: (e) 10 km, (f) 15 km] [Observations from 4 verify rain gauges also superimposed on radar rainfall estimates in (d)] |
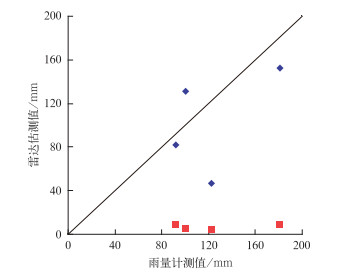
表 1为4个检验站雨量计测值及不同校准方法雷达估测降水(该雨量计上空及周围共9个格点估测值平均)及精度评估,评估方法为相对误差法(相对误差取绝对值)。表中Rg为雨量计测值,Ra和rea分别为平均校准结果及相对误差,Rcla10(Rcla15)和recla10(recla15)分别为10 km(15 km)校准半径局地分级平均校准结果及相对误差,Rla10(Rla15)和rela10(rela15)分别为10 km(15 km)校准半径局地平均校准结果及相对误差。结果表明,10 km校准半径局地分级平均校准结果的平均相对误差最小,为34.8%。如果先对4个检验站测值和反演结果求平均,然后再计算相对误差,则10 km局地分级校准结果的相对误差只有16.7%,15 km校准半径局地分级平均的为28.6%,10 km校准半径局地平均的为32.9%,15 km校准半径局地平均的为44.7%,平均校准的为68.2%(表略)。表明10 km局地分级平均校准的效果较其他方法好。可见,局地分级平均校准法较局地平均校准法对强降水的估测效果好,同时两种方法的降水估测效果均与所取的局地校准半径大小有关。图 5为校准前及10 km局地分级平均校准后4个检验站的结果与雨量计测值散点图,表明校准后的结果更加接近1:1线。本文第3节将利用10 km局地分级平均校准得到的结果对短时强降水分布与荣昌吴家镇双流村洪水气象风险关系进行分析。
|
|
表 1 4个检验站雨量计测值及不同校准方法雷达估测降水及精度评估 Table 1 Rain gauge observations and radar rainfall estimates from different algorithms and accuracy evaluation for the 4 rerifying stations |
|
图 5 校准前(红色)及10 km局地分级平均校准后(蓝色)4个检验站雷达估测降水与雨量计测值散点图 Fig. 5 Scatter plots of radar estimates and rain gauge observations for the 4 verifying stations (red: before adjustment, blue: after using local classified average bias-adjusted algorithm with 10 km local adjustment radius) |
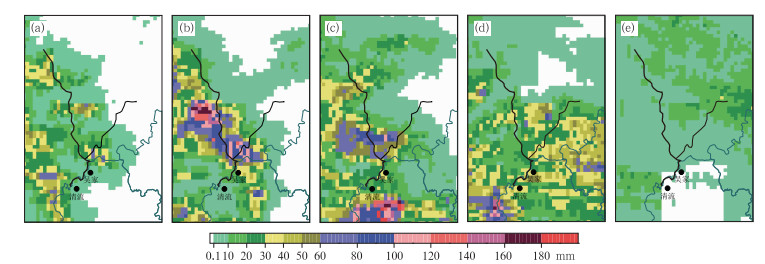
图 6为10 km校准半径局地分级平均校准法得到的2012年7月21日21:00至22日01:00的逐时(图 6a~6e)雷达定量降水估测结果。图中叠加了荣昌清流镇以上的大清流河主要河网。粗黑实线为干流,细黑实线为支流。大清流河(《中国河湖大典》,2010) 为沱江左岸较大支流,河长122 km,流域面积为1554 km2。大清流河发源于四川省安岳县,干流(图 6中粗黑实线)河道曲折向南偏东,至松林坝,左纳大支流小清流河(图 6中细黑实线)。河流向南入重庆市荣昌县,过吴家镇,再西南,有一段为四川内江、重庆荣昌界河。再以下过荣昌县清流镇,再转西入内江市境。最后于内江大河口汇入沱江。分析图 6发现,21日21:00时,大清流河干流源头反演出最强50 mm·h-1以上的强降水,干流中游和支流下游有80 mm·h-1以上的强降水。22:00时,从干流源头到干、支流交汇点全线发生短时强降水,干流中游反演出的强降水高达160~180 mm·h-1。23:00时,短时强降水主要集中在干、支流交汇点以上,反演的小时降水个别地方仍有100 mm·h-1以上。22日00:00时,吴家镇以上降水有所减弱,但干流和支流之间仍有个别地方反演小时降水达到80 mm·h-1以上。因此,吴家镇以上沿干流全线和支流下游的强降水,以及强降水中心沿干流从上游向下游移动,是造成吴家镇双流村等地洪水的主要原因。7月22日凌晨01:00,吴家镇双流村水位暴涨,若以干流最强降水发生在21日22:00计算,洪水发生相对于强降水发生的响应时间为3 h左右。因此,结合河网分布情况,对短时强降水分布的监测有助于提前做出中小河流洪水气象风险预警预报。
|
图 6 局地分级平均校准法得到的2012年7月21日21:00至22日01:00 BT逐时雷达定量估测降水 (a) 2012年7月21日21:00 BT,(b) 2012年7月21日22:00 BT,(c) 2012年7月21日23:00 BT,(d) 2012年7月22日00:00 BT,(e) 2012年7月22日01:00 BT Fig. 6 Radar rainfall estimates at 21:00 BT (a), 22:00 BT (b) and 23:00 BT (c) 21 July and 00:00 BT (d) and 01:00 BT (e) 22 July 2012 obtained by local average bias-adjusted algorithm |
本文的个例分析表明:
(1) 局地分级平均校准法较局地平均校准法对强降水的估测效果好,同时两种方法的降水估测效果均与所取的局地校准半径大小有关。
(2) 对降水分布及洪水灾情的分析表明,降水分布与河网的结合是进行中小河流洪水气象风险预报的重要着眼点。
在进行局地分级平均校准或局地平均校准的雷达定量降水估测时,不同的降水类型和雨量计密度会影响到局地校准半径和最小雨量计数的选择。由于降水类型多变,因此雨量计密度是选取最小雨量计数的重要依据。例如,如果雨量计密度为每50 km2 1个雨量计,则10 km半径范围内约有6个雨量计,可以取其1/2,得到3个雨量计左右作为最小雨量计数。
为了帮助预报员快速判断和预报中小河流洪水气象风险等级,需要发展建立中小河流洪水气象风险等级预报指标的方法。目前常用的方法之一是对有水文观测资料的流域,根据警戒水位、保证水位以及历史流量和降水资料,通过统计方法或水文模拟方法建立洪水气象风险等级累积面雨量等预报指标(Montesarchio et al,2009;张亚萍等,2012)。然而,洪水不一定发生在流域出口,在考虑地理信息的基础上,降水的时空分布是导致区域洪水的直接原因,是今后建立中心河流洪水气象风险等级预报指标时需要关注的方面。
樊建勇, 单九生, 管珉, 等, 2012. 江西省小流域山洪灾害临界雨量计算分析[J]. 气象, 38(9): 1110-1114. |
李建通, 高守亭, 郭林, 等, 2009. 基于分步校准的区域降水量估测方法研究[J]. 大气科学, 33(3): 501-512. |
李向红, 唐熠, 郑传新, 等, 2010. 一次多种强对流天气过程的雷达回波特征分析[J]. 气象, 36(8): 61-71. DOI:10.7519/j.issn.1000-0526.2010.08.009 |
刘晓阳, 杨洪平, 李建通, 等, 2010. 新一代天气雷达定量降水估测集成系统[J]. 气象, 36(4): 90-95. DOI:10.7519/j.issn.1000-0526.2010.04.016 |
慕建利, 李泽椿, 谌芸, 2012. 一次强暴雨过程地闪活动特征与中尺度对流系统和强降水的关系[J]. 气象, 38(1): 56-65. DOI:10.7519/j.issn.1000-0526.2012.01.006 |
彭涛, 宋星原, 殷志远, 等, 2010. 雷达定量降水估算在水文模式汛期洪水预报中的应用试验[J]. 气象, 36(12): 50-55. DOI:10.7519/j.issn.1000-0526.2010.12.007 |
曲晓波, 张涛, 刘鑫华, 等, 2010. 舟曲"8.8"特大山洪泥石流灾害气象成因分析[J]. 气象, 36(10): 102-105. DOI:10.7519/j.issn.1000-0526.2010.10.017 |
田付友, 程明虎, 张亚萍, 等, 2010. 校准雨量计密度对雷达联合雨量计估测流域平均面雨量的影响[J]. 气象学报, 68(5): 717-730. DOI:10.11676/qxxb2010.069 |
汪瑛, 冯业荣, 蔡锦辉, 等, 2011. 雷达定量降水动态分级Z-I关系估算方法[J]. 热带气象学报, 27(4): 601-608. |
张家国, 岳阳, 牛淑贞, 等, 2010. 一次长历时特大暴雨多普勒雷达中尺度分析[J]. 气象, 36(4): 21-26. DOI:10.7519/j.issn.1000-0526.2010.04.004 |
张利平, 李璐, 叶爱中, 等, 2007. 雷达联合雨量计估算区域降水量精度对比[J]. 武汉大学学报:工学版, 40(1): 1-5. |
张亚萍, 程明虎, 徐慧, 等, 2007. 雷达定量测量降水在佛子岭流域径流模拟中的应用[J]. 应用气象学报, 18(3): 295-305. |
张亚萍, 刘德, 廖峻, 等, 2012. 一种基于水文模拟建立中小河流洪水气象风险等级指标的方法[J]. 暴雨灾害, 31(4): 351-357. |
张亚萍, 沃伟峰, 刘德, 等, 2013. 基于精细化降水分布的山洪气象条件分析[J]. 气象, 39(1): 101-111. DOI:10.7519/j.issn.1000-0526.2013.01.013 |
赵琳娜, 包红军, 田付友, 等, 2012. 水文气象研究进展[J]. 气象, 38(2): 147-154. DOI:10.11898/1001-7313.20120203 |
《中国河湖大典》编纂委员会编著, 2010. 中国河湖大典(长江卷, 上)[M]. 北京: 中国水利水电出版社, 510.
|
Baeck M L, Smith J A, 1998. Rainfall estimation by the WSR-88D for heavy rainfall events[J]. Wea Forecasting, 13: 416-436. DOI:10.1175/1520-0434(1998)013<0416:REBTWF>2.0.CO;2 |
Bauer-Messmer B, Smith J, Baeck M, et al, 1997. Heavy rainfall: Contrasting two concurrent Great Plains thunderstorms[J]. Wea Forecasting, 12: 785-798. DOI:10.1175/1520-0434(1997)012<0785:HRCTCG>2.0.CO;2 |
Fulton R A, 1999. Sensitivity of WSR-88D rainfall estimates to the rain-rate threshold and rain gauge adjustment: A flash flood case study[J]. Wea Forecasting, 14: 604-624. DOI:10.1175/1520-0434(1999)014<0604:SOWRET>2.0.CO;2 |
Fulton R A, Breidenbach J P, Seo D, et al, 1998. The WSR-88D rainfall algorithm[J]. Wea Forecasting, 13: 377-395. DOI:10.1175/1520-0434(1998)013<0377:TWRA>2.0.CO;2 |
Kitzmiller D, Cooten S V, Ding F, et al, 2011. Evolving multisensor precipitation estimation methods: Their impacts on flow prediction using a distributed hydrologic model[J]. J Hydrometeor, 12: 1414-1431. DOI:10.1175/JHM-D-10-05038.1 |
Marshall J S, Palmer W McK, 1948. The distribution of raindrops with size[J]. J Meteor, 5: 165-166. DOI:10.1175/1520-0469(1948)005<0165:TDORWS>2.0.CO;2 |
McEnery J, Ingram J, Duan Q Y, et al, 2005. NOAA's advanced hydrologic prediction service-building pathways for better science in water forecasting[J]. Bull Amer Meteorol Soc, 86: 375-385. DOI:10.1175/BAMS-86-3-375 |
Montesarchio V, Lombardo F, Napolitano F, 2009. Rainfall thresholds and flood warning: An operative case study[J]. Nat Hazards Earth Syst Sci, 9: 135-144. DOI:10.5194/nhess-9-135-2009 |
Smith J A, Baeck M L, Steiner M, et al, 1996. Catastrophic rainfall from an upslope thunderstorm in the central appalachians: The rapidan storm of June 27, 1995[J]. Water Resour Res, 32: 3099-3113. DOI:10.1029/96WR02107 |
Willis P T, Tattelman P, 1989. Drop-size distributions associated with intense rainfall[J]. J Appl Meteor, 28: 3-15. DOI:10.1175/1520-0450(1989)028<0003:DSDAWI>2.0.CO;2 |
Wilson J W, Brandes E A, 1979. Radar measurement of rainfall——A summary[J]. Bull Amer Meteor Soc, 60: 1048-1058. DOI:10.1175/1520-0477(1979)060<1048:RMORS>2.0.CO;2 |
 2013, Vol. 39
2013, Vol. 39 