2. 浙江慈溪市气象局,慈溪 315300;
3. 上海台风研究所,上海 200030
2. Cixi Meteorological Office of Zhejiang Province, Cixi 315300;
3. Shanghai Typhoon Institute, CMA, Shanghai 200030
目前国内外各预报中心一直致力于热带气旋(TC)强度业务预报的改进(陈联寿,2006;许映龙等,2010)。但由于影响台风强度变化的因素众多,且十分复杂,在相关资料或数值模式(特别是海气耦合台风数值预报模式)没有大幅度改善之前,利用相关研究成果以及业务预报中积累的经验,提取与TC强度变化密切相关的因子,应用动力统计方法进行TC强度预报仍然是一个十分重要的课题(端义宏等,2005)。近几年国内已有多项研究工作与此相关,如利用欧洲中期预报场及气候持续预报因子建立的统计释用预报方法(简称STC)(胡春梅等,2006)、气候持续预报方法(简称TICP)(余晖等,2001)和针对南海TC的基于遗传-神经网络的TC强度预报方法(姚才等,2007) 以及用统计方法分析气候持续因子、起报时刻天气因子、当前及未来TC可能影响区域海温等因子做热带气旋强度预报(Chen et al, 2011;宋金杰等,2011)。近海及登陆TC强度变化受地形等下垫面情况影响而变得异常复杂,然而在目前准业务运行和业务运行的台风强度预报方法中,除部分方法在建模时一定程度上考虑了近海样本外,并没有对这类样本进行特殊的处理,导致该类样本预报误差较大(李英等,2004)。但是近海及登陆TC的强度预报准确性对防灾减灾的影响更为直接,因此更为重要。
Vapnik等(1963) 提出的统计学习理论(Bretherton, 1992) 是一种专门的小样本理论,基于这一理论近年提出的支持向量机(Support Vector Machines, SVM)方法,避免了人工神经网络等方法中网络结构难以确定、过学习和欠学习以及局部极小等问题,为解决非线性问题提供了一个新思路。SVM回归方法是依据支持向量(关键样本)来建立最终的决策函数,这一特征与基于确定因子的权重系数来明确表达各个因子的权重组合与预报对象变化的常规统计方法(如逐步回归、卡尔曼滤波和神经网络)有显著的区别。SVM方法考究的是因子群构造的样本空间与预报对象的关系,单个因子与预报对象是否具有显著相关并不重要,而且不需要很大的样本数(陈永义等,2004;冯汉中等,2004)。
气象上用SVM方法做各种要素预报以及数值释用预报,已有了许多尝试(黄崇福等,1995),如温度预报,能见度预报,降水预报,台风影响时的风力预报(熊秋芬等,2008;钱燕珍等,2012;黄丽娜等,2009)等,取得了很好的效果和应用。我们试图利用SVM方法,对相对稳定的环境场数值预报结果进行解释应用,结合TC自身情况,从距离角度来考虑地形对热带气旋不同阶段强度的影响等,做近海及登陆TC的强度预报,并把预报结果分别与中央气象台的预报结果和气候持续法预报结果进行比较。
1 资料和TC强度预报思路使用1999—2009年1°×1°的NCEP再分析场资料,来自台风年鉴的路径、强度资料以及经纬度分辨率0.5°×0.5°的地形资料。其中1999—2008年用于建立模型,2009年资料作为独立样本,检验模型的预报能力。用2009和2010年14个TC的GFS数值预报产品和中央气象台对TC路径的预报产品来检验模型的实际业务预报水平。
建模的TC,一天取4个时次样本。选择进入第一警戒线以后强度在热带风暴以上的TC,从进入第一警戒区开始到在警戒区内刚减弱为热带低压这个时次,包括减弱为热带气压时的头一个时次,这中间所有02、08、14和20时次的强度资料,作为样本。整理资料后,拟合建模资料共计有115个TC,2009年的检验TC是13个。对2009和2010年中央台编号“200904”,“200907”,“200908”,“200913”,“200915”,“200916”,“201002”,“201003”,“201004”,“201006”,“201007”,“201010”,“201011”和“201013”共14个TC进行实际业务应用检验。
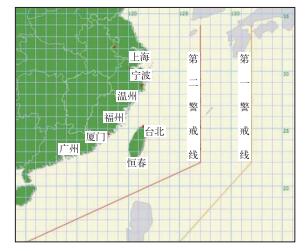
|
图 1 热带气旋警戒线示意图 Fig. 1 Warning region of tropical cyclones |
强度预报模式不直接对预报时次的TC强度进行预报,而是预报该时次相对与实况的强度增量。根据TC强度变化的一些机理和平时预报经验,从TC本身强度、影响范围内的环境场气象要素以及地形资料,寻找相关因子,利用TC实况资料,NCEP再分析场资料,应用支持向量机径向基函数的方法分别对12、24、36、48、60和72 h共6个预报时次,建立预报模型。在实际预报工作中,利用数值预报结果,就可以实现近海及登陆TC的72 h内强度预报。
2 相关因子设计和计算 2.1 从三个方面设计相关因子(1) TC本身强度
包括实况的近中心最大风速、最低气压和中心所在位置的经纬度。
(2) TC影响范围内的气象要素因子
影响范围内,包括1000、925、850、700和500 hPa共5层各网格点上的温度、相对湿度、绝对涡度、垂直上升速度、两分钟平均风速,以及925~500 hPa的位势高度和海平面气压。
各TC的影响范围直径通常从五、六百千米到两千多千米(陈联寿等,1979)。由于目前还没有明确的TC影响范围数据,且每个TC差别很大,为便于计算,统一设定每个TC影响范围的半径为8个经纬度。
(3) 地形因子
包括TC中心到大陆海岸线的距离,TC中心到台湾的距离,影响范围内各网格点的海拔。
2.2 相关因子计算根据相关因子的计算方法,可分为点因子和面因子。
2.2.1 点因子计算点因子主要是单个标量,不涉及TC的影响范围。包括:TC中心的经纬度、TC中心附近实况最大风速和最低气压等。
TC中心到大陆海岸线的距离:计算TC中心到最近海岸线的距离,若TC中心在海洋上,则设定为正,若在陆地上,则为负。
TC中心到台湾的距离:以台湾的地理中心点(23.58′32″N、120.58′25″E)作为台湾地理位置的代表,计算TC中心到台湾地理中心点的距离。
|
|
表 1 相同时次TC近中心最大风速与标量因子的相关系数 Table 1 The correlation coefficient of maximum wind speed near TC center and scalar factors at the same time |
面因子,主要是场变量在影响范围内的累计平均值。一般认为:各变量对TC中心强度的影响,随着格点到TC中心距离的增大而减小。加入距离权重系数,计算影响范围内相关因子的累计平均值。
计算公式:
| $ {{\bar T}_s} = \frac{1}{{2{\rm{\pi }}R}}\int_0^{2\pi } {\int_0^R {f\left( r \right)T{\rm{d}}r{\rm{d}}\theta } } $ |
式中,T为相关因子,r是以TC中心为圆心,网格点到圆心的距离,R为TC影响范围半径,设定为8个经纬度。
网格差分计算:
| $ {{\bar T}_s} = \frac{1}{M}\sum\limits_i^M {F\left(r \right){T_i}} $ |
式中,M为影响范围内的格点数,F(r)为气象要素对TC强度的影响函数。
目前有关气象要素对TC强度的影响,随影响半径变化的具体规律研究较少。现设定4个影响函数,粗略探索其影响程度随半径的变化情况。
(1) F(r)=1 即:相关因子在影响范围内所有网格点上的平均值。假定相关因子对TC中心强度的影响程度不随影响半径变化。
(2)
(3)
(4)
从TC本身、环境场因素和地形因素三个方面出发,共构造了44个因子,通过对44个预报因子和所预报各时次的极大风速、最低气压相关性分析,表明绝大部分因子可以通过置信度为0.05的F检验。
对TC近中心最大风速(最低气压的相关系数也类似,不再列举)与同一时次的相关因子做相关分析,结果如表 2。根据影响程度随半径的4种变化情况的相关性分析,选定该要素最合适的影响程度随半径的变化模型。大多数相关因子都选用影响程度随影响半径增大而减速递减的第四种模型。
|
|
表 2 TC的近中心最大风速与因子相关系数的4种计算方法比较 Table 2 Comparison of the 4 calculation methods for the correlation between maximum wind speed near TC center and its factors |
由表 2可见,TC内力的惯性作用主要体现在36 h以内,TC本身因素和地形因素在这一时段作用大一些。随着预报时效的延长,相邻时段气象要素的差值与TC强度变化的相关性明显增强,36 h后成为主要影响要素,也就是36 h后环境场的影响对TC强度的变化起主导作用。
2.4 相关因子的进一步筛选以上相关性分析都是同一时次的,现对各相关因子分别在实况和预报两个时次的值,与预报时次的TC中心强度相对实况时次的增量做进一步分析。
选择TC中心的实况最大风速和最低气压,实况和预报两个时次的TC中心的经纬度、海拔和到海岸线的距离,每种气象要素在不同层次中相关性最好的1~2个,以及同一个相关因子在预报时次的值和实况时次的值的差(预报时次的值减实况时次的值),共计44个相关因子。不同预报时次的相关性计算结果数值不同,但相差不多,其中各因子与72 h最大风速增量的相关性结果如表 3,其他表略。
|
|
表 3 各因子与最大风速72 h增量的相关性 Table 3 The correlation between the increment of maximum wind speed near TC center in 72 h and the factors |
从计算结果分析得到:
(1) 0~12 h时段的TC强度变化过程中,温度、湿度等环境因子在实况时段比同一时次的相关性更大,说明TC强度变化有较大的惯性,外界环境场因子的变化至少需要24 h以后才能较大程度地改变TC强度。
(2) 影响范围内的风速、涡度和垂直速度等因子一定程度上体现了TC的整体强度,因而在相同时次,其与TC中心强度的相关性比不同时次的更好。
(3) 相同因子在不同时次的差值,随着预报时次的增大,相关性也在增大。在长时效的TC强度预报中,需要更多的考虑影响环境的变化,其本身的强度次之。
3 模型的建立和拟合 3.1 支持向量机方法建模支持向量机的函数回归模式的核函数采用径向基函数,训练工具采用台湾大学林智仁等开发的LibSVM软件中的ν-SVM回归模式。径向基函数的表达式为:
| $ {\rm{exp}}(- 0.15 \times |\mathit{\boldsymbol{U}} - {\mathit{\boldsymbol{V}}_i}{|^2}) $ |
其中,U为预报因子向量,Vi为支持向量。
根据各因子的相关性、物理意义的主观分析和多次试验,对不同时次的TC近中心最大风速和最低气压分别建立相关预报模型(表 4)。由表 4可见,每个时次,中心最大风速和最低气压增量预报因子都有一些不同,但几乎都包含了TC自身因子、地形因素和环境场因子。
|
|
表 4 TC强度预报模型采用的因子和训练参数 Table 4 The factors and parameters of the model used in TC intensity prediction |
模型的拟合训练结果如表 5。
|
|
表 5 各时次TC强度拟合结果 Table 5 The fitting results of TC intensity of each time |
由表 5可见,不管是风速拟合的复相关系数,还是气压拟合的复相关系数,都是很高的,说明所选因子有很好的代表性,可以作为支持向量模型预报的因子。各个时次的风速绝对值误差都不是很大,而且随着预报时效的增长,误差并没有明显增大。误差的标准差也同样不是很大,随着预报时效的增大也没有明显增大。气压的拟合也呈现了同样的效果,拟合的绝对值误差和标准差都不是很大,并且随着预报时效的增长,误差没有明显增大。
4 独立样本检验使用2009年13个进入模型所规定范围内的TC的实况路径资料和NCEP再分析场资料,对预报模式可能达到的最佳预报能力进行检验,如表 6。
|
|
表 6 2009年各时次TC强度独立检验结果 Table 6 Independent test for TC intensity prediction of each time in 2009 |
由表 6可见,12 h极大风速绝对值误差接近3 m·s-1,中心最低气压绝对值误差接近5 hPa,还是比较小的。风速误差最大出现在60 h预报,极大风速绝对值误差5.17 m·s-1,中心最低气压绝对值误差最大出现在72 h,值是8.90 hPa,总体上检验结果还是比较好的。
5 业务检验 5.1 强度预报的业务检验对2009—2010年14个TC进行业务检验。数值预报资料使用的GFS预报资料。预报结果与同时次的中央气象台预报、气候持续法预报结果比较,总体误差如表 7和表 8。
|
|
表 7 三种预报方法对TC各时次的近中心最大风速的预报误差 Table 7 The prediction errors of maximum wind speed near TC center predicted by three prediction methods |
|
|
表 8 两种预报方法对TC各时次的最低气压的预报误差 Table 8 The prediction errors of lowest pressure predicted by two prediction methods |
(1) 本模式的预报效果与稳定性均优于气候持续法。
(2) 本模式和中央气象台的预报比较,48 h及之前的效果略差,72 h的预报略好于中央气象台。总体效果略差于中央气象台,但差距不大。
本模式与中央气象台对各个TC的具体预报效果(图略)互有高低,相差不是很大。极大风速的预报结果比较接近;近中心最低气压48 h之前,略差于中央气象台的预报,其他时次比较接近。与气候持续法相比,多数个例都优势明显。
5.2 强度变化趋势的业务检验对于TC强度变化的趋势的判断,在实际的TC预报服务工作中,也有较大意义。通过比较TC预报强度变化趋势(增强还是减弱)与实际变化趋势一致性,也能反映预报模式的好坏。现定义:
| $ {\rm{预报趋势一致率}} = \frac{{\rm{预报变化率趋势与实况变化趋势一致的时次数}}}{{\rm{总的预报时次数}}} \times 100\% $ |
计算结果如表 9。
|
|
表 9 三种预报方法对TC中心最大风速和最低气压的各时次的预报趋势一致率 Table 9 The prediction coincidence rate of maximum wind speed and lowest pressure near TC center by three prediction methods |
从表 9可见,对TC强度变化趋势的预报,本模式要优于其他两种方法。尤其是长时效的趋势预报,效果更好,可高出7~12个百分点。
5.3 台风及以上级别TC和靠近大陆TC的业务检验鉴于实际业务中,对大强度TC的关注度更高。现对TC实况强度达到台风及以上(近中心最大风速≥32 m·s-1)时次的近中心最大风速预报误差进行统计(表 10),比较三种预报方法间的差异。
|
|
表 10 三种预报方法对近中心最大风速≥32 m·s-1的各时次的最大风速预报误差 Table 10 The prediction errors of maximum wind speed over 32 m·s-1 near TC center predicted by three prediction methods |
由于TC近海和登陆影响比较大,现对各TC实况位置出现在15 °N以北,121°E以西的以大陆为主体区域内各时次的距离预报误差统计分析(表 11),比较三种预报方法间的差异。
|
|
表 11 三种预报方法对实况位置出现在大陆及附近TC的最大风速预报误差 Table 11 The prediction errors of maximum wind speed of TC near and on the land predicted by three methods |
对于近中心最大风速≥32 m·s-1和大陆主体区域内的TC强度预报(表 10和表 11),本模式与中央气象台预报的差异总体上接近,48 h及之前,差于中央气象台的预报,72 h略优于该预报。总体上都明显优于气候持续法的预报。
6 结论本工作针对近海和登陆TC,用支持向量机方法对GFS数值预报产品进行解释应用,做强度预报。在构造预报因子时,考虑了数值预报相对稳定的环境场因子,TC自身因子,地形因子(从距离角度来考虑地形对热带气旋不同阶段强度的影响)等,用来预报12、24、36、48、60和72 h的TC强度。实际业务应用检验,6个时效风速预报业务检验误差的标准差分别是:4.85、6.34、7.69、7.71、8.23和7.22 m·s-1,平均绝对值误差分别是:3.94、5.28、6.26、6.47、6.87和6.12 m·s-1;气压预报业务误差标准差分别是:8.33、10.99、13.13、13.46、14.08和13.91 hPa。平均绝对值误差:6.26、8.56、10.50、10.73、11. 31和11.42 hPa。通过各种分析可以得到:
(1) 本模式的强度预报效果总体上比中央气象台的强度预报效果略差,但差距不大。24和48 h时效预报,中央台预报效果略好;72 h预报,本模式的效果略优。从强度变化趋势预报的效果来看,本模式相比中央气象台的预报有较明显优势,尤其是长时效的趋势预报,效果更好,可高出7~12个百分点。说明本强度预报模式在实际台风预报工作中具有应用价值。
(2) 通过和气候持续法的预报效果比较,本模式从预报效果和稳定性等方面均优于气候持续法。
(3) 本预报模式的预报精度主要取决于GFS数值预报产品,因而随着数值预报产品精度的提高,模式的预报准确率也能进一步提高。
陈联寿, 丁一汇, 1979. 西北太平洋台风概论[M]. 北京: 科学出版社, 1-491.
|
陈联寿, 2006. 热带气旋研究和业务预报技术的发展[J]. 应用气象学报, 17(6): 672-681. DOI:10.11898/1001-7313.20060605 |
陈永义, 俞小鼎, 高学浩, 等, 2004. 处理非线性分类和回归问题的一种新方法(Ⅰ)——支持向量机方法简介[J]. 应用气象学报, 15(3): 345-354. |
端义宏, 余晖, 伍荣生, 2005. 热带气旋强度变化研究进展[J]. 气象学报, 63(5): 636-645. DOI:10.11676/qxxb2005.062 |
冯汉中, 陈永义, 2004. 处理非线性分类和回归问题的一种新方法(Ⅱ)——支持向量机方法在天气预报中的应用[J]. 应用气象学报, 15(3): 355-365. |
胡春梅, 余晖, 陈佩燕, 2006. 西北太平洋热带气旋强度统计释用预报方法研究[J]. 气象, 32(8): 64-69. DOI:10.7519/j.issn.1000-0526.2006.08.011 |
黄崇福, 王家鼎, 1995. 模糊信息优化处理技术及其应用[M]. 北京: 北京航空航天大学出版社.
|
黄丽娜, 林笑茹, 曾华, 等, 2009. 西北太平洋台风累积动能的气候特征[J]. 气象, 35(9): 44-50. DOI:10.7519/j.issn.1000-0526.2009.09.006 |
李英, 陈联寿, 王继志, 2004. 登陆热带气旋长久维持与迅速消亡的大尺度环流特征[J]. 气象学报, 62(2): 167-179. DOI:10.11676/qxxb2004.018 |
钱燕珍, 孙军波, 余晖, 等, 2012. 用支持向量机方法做登陆热带气旋站点大风预报[J]. 气象, 38(3): 302-308. |
宋金杰, 王元, 陈佩燕, 等, 2011. 基于偏最小二乘回归理论的西北太平洋热带气旋强度统计预报方法[J]. 气象学报, 69(5): 745-756. DOI:10.11676/qxxb2011.066 |
熊秋芬, 曾晓表, 2008. SVM方法在降水预报中的应用及改进[J]. 气象, 34(12): 90-95. DOI:10.7519/j.issn.1000-0526.2008.12.012 |
许映龙, 张玲, 高拴柱, 2010. 我国台风预报业务的现状及思考[J]. 气象, 36(7): 43-49. DOI:10.7519/j.issn.1000-0526.2010.07.009 |
姚才, 金龙, 黄明策, 等, 2007. 遗传算法与神经网络相结合的热带气旋强度预报方法试验[J]. 海洋学报, 29(4): 11-19. |
余晖, 薛宗元, 2001. 若干统计方法预测影响华东地区热带气旋年频数的对比试验[M]. 上海: 大气科学研究与应用.
|
Bretherton C S, 1992. An intercomparison of methods for finding coupled patterns in climate datce[J]. J Climate, 5(6): 541-560. DOI:10.1175/1520-0442(1992)005<0541:AIOMFF>2.0.CO;2 |
Chen Peiyan, Yu Hui, Chan Johnny C L, 2011. A western North Pacific tropical cyclone intensity predition scheme[J]. Acta Meteor Sin, 05: 611-624. |
Vapnik V, Lerner A, 1963. Pattern recognition using generalized portraits[J]. Avtomatikai Telemekhanika, 24: 774-780. |
 2013, Vol. 39
2013, Vol. 39 