目前天气预报业务和模式研究中常用的降水检验方法是TS评分、ETS评分和均方根误差等基于点对点的检验(Jollife et al, 2003),此类方法的特点是可对预报结果的优劣给出一个综合评价,但却无法对预报中更为关注的强降水带位置、范围和强度等属性给出定量检验结果。周慧等(2010) 检验分析了T639模式对2008年5月26日20时至27日02时长江中下游暴雨雨带属性的预报,但其检验主要通过主观分析进行,缺乏客观定量的检验结果。Davis等(2006a)仔细分析了TS评分方法存在的问题和基于目标的降水检验方法的应用价值。Davis等(2006a;2006b;2009)、Marzban等(2006)和Gilleland等(2008) 逐步开展了基于目标的降水检验方法研究。Davis等(2006a;2006b;2009) 在研究中将降水量大于给定阈值的每一片互相连通的区域作为一个降水目标。而Marzban等(2006) 在进行降水目标识别时采用聚类分析的方法对目标进行逐步合并,从而形成少数几个和直观判断相近的降水目标。Gilleland等(2008) 提出了对预报场和观测场中的降水目标进行配对的算法步骤,能让配对的方式接近最优,同时保证所需计算量较少。在对降水目标实现识别和配对的基础上,Davis等(2009)、Nachamkin(2004)和Lack等(2010) 提出了各种对降水目标进行检验的方法。
在已有的研究中,基于目标的降水检验方法的算法流程已经发展成型,但目前它在业务中的应用还很少,为此,有必要对此类方法进行总结和介绍。另外,已有算法中的具体算子还需进一步改进被以使目标识别和配对的结果更加合理。本文将通过理论分析结合大量实例研究提出更为合理的算子,从而改进此类检验方法,并结合目前主流业务模式降水预报产品开展实例应用研究。
1 资料本文选用的资料为2010和2011年中每年5—9月逐日0800 BT 24 h降水量加密观测资料(全国共计2513个站),以及国家气象中心全球谱模式T639 L60(简称T639模式)(管成功等,2008)、欧洲中期天气预报中心(简称ECMWF)和日本模式的降水要素预报资料。
2 基于目标的降水检验方法基于目标的检验的基本思想是将降水场看作天气系统相伴随的多个降水目标组成,它对观测场和预报场中的降水目标识别和配对后再进行检验,以提供具有天气学含义的定量检验信息。基于目标的降水检验方法包含三个基本的步骤:目标识别、目标配对和目标检验。
2.1 目标识别目标识别是从原始的降水场中提取大于一定量级的降水区域并将它划分成少数几个降水目标,其中关键内容是逐步地将小的目标合并成大的目标。目标识别过程实际上是一个聚类分析的过程(Marzban et al,2006),其步骤如下:
步骤1,设定一个阈值α,找出观测场或预报场中降水值大于α的观测点或格点,每一个观测点或格点作为一个初始的目标。
步骤2,计算各个目标两两之间的临近度,找出最为临近的两个目标,若它们之间的临近度大于给定阈值β则合并作为一个目标。重复步骤2,直到所有的目标之间的临近度都小于β,则算法终止,所剩目标即为算法识别出的降水目标。
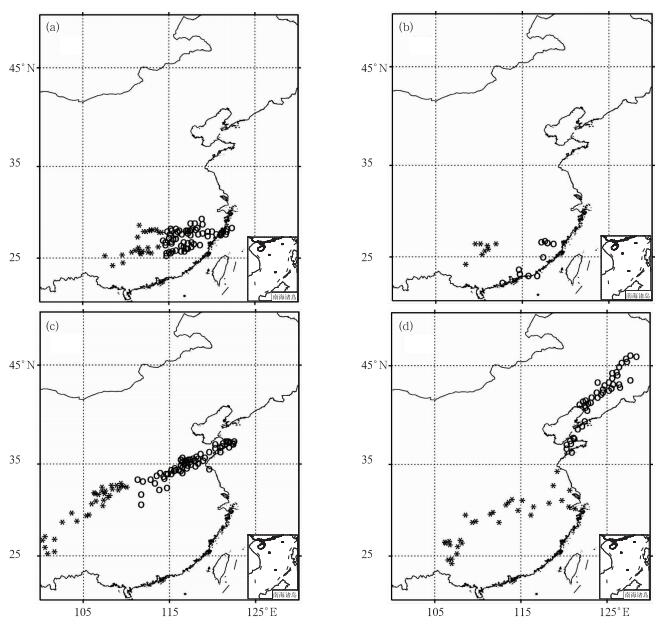
算法中目标之间临近度的定义决定了最终目标识别的结果,其定义越合理,目标识别的结果越合理。降水目标实际上是像素点(观测点或格点)的集合,已有的研究中通常采用点集之间的距离的倒数作为临近度(Marzban et al, 2006;Gilleland et al, 2008;Venugopal et al, 2005),目标之间距离越大,越不该合并。常用的点集之间的距离定义有平均距离、最近距离、最远距离和最大近距(Marzban et al, 2006;Gilleland et al, 2008;Venugopal et al, 2005)。本文挑选了4个典型的例子来说明这4种计算方式容易出现的问题。这4个例子分别来自2010年5月13日、6月13日、7月17日和7月20日08时的24 h累积降水分布。每个例子中有A和B两个待判别的目标,分别用“*”和“o”表示(图 1),它们都是大于50 mm的降水目标。本文计算了每个例子中目标A和B的临近度(见表 1)。选择一个合适的阈值,以此判断A和B是否应该合并,并与人工判断的结果对比。选择和人工判断进行对比,并非将人工判断作为绝对的标准,之所以这样做主要基于两点考虑:一是没有一种绝对合理的客观标准可作为参考;另外人工判断往往更容易综合一些复杂因素得出较为合理的判断,至少在那些人工容易判断的情况下,一个好的客观方法判断的结果应该与人工判断的结果一致。
|
图 1 待判别的目标实例,Ⅰ、Ⅱ、Ⅲ和Ⅳ分别来自2010年5月13日(a)、6月13日(b)、7月17日(c)和7月20日(d)08时的24 h累积降水大于50 mm的降水目标 (“*”和“o”分别属于目标A和B的像素点) Fig. 1 Cases of object pairs required to distinguish, Ⅰ, Ⅱ, Ⅲ and Ⅳ are respectively 50 mm object pairs of 24 h cumulative rainfall at 08:00 BT (a) 13 May, (b) 13 June, (c) 17 July, and (d) 20 July 2010 ("*" and "o" are pixels of objects A and B) |
|
|
表 1 各个实例的临近度及人工对目标合并与否的判别 Table 1 The close degree and manual judgement of the objects to be merged or not in each case |
结合图 1和表 1进行分析,例Ⅰ的两个目标整体接近,主观判断应该合并,但是两个目标最远距离较大,若采用最远距离作为判别标准,则容易误判成不该合并。例Ⅱ,A和B两个目标明显分离,主观判断是两个独立的目标,但由于它们的尺度都较小,因此平均距离、最远距离和最大近距都较小,如果采用这些作为标准,容易误判成应该合并。例Ⅲ是一个降水雨带中间出现小段间隙,从而分裂成了A和B两个目标,主观判断它们是同一个雨带,应该合并,但由于目标尺度很大,因此平均距离、最远距离和最大近距都很大,容易误判成独立的两个目标。例Ⅳ中A和B两个降水目标主体相距很远,雨带走向也不同,主观判断它们不该被合并,但是B的一个小部分落在离A非常近的地方,最近距离较小,因此采用最近距离容易误判成应该合并。
比较这4种度量方式,可知最远距离是一种最不稳定的度量,很容易将一个尺度较大的目标判断成两个目标,而将尺度较小的两个目标判断成一个目标;最近距离是一种相对稳定的度量,但是容易将主体相距较远但有很小部分接近的两个目标误判成一个目标;平均距离和最大近距的性能介于最小距离和最大距离之间。
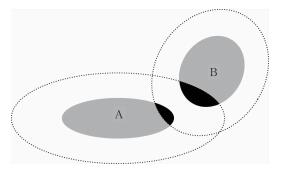
考虑到已有临近度定义存在的问题,本文提出一种更为合理的临近度的定义方法。通过分析可知,两个目标临近度不单由距离决定,至少还需考虑面积和形状的因素。当判断两个目标整体上临近时,实际是指一个目标中的很大部分处于另一个目标的附近。本文以图 2来示意说明,图 2中有A和B两个目标,以填色区域表示,目标A和B有各自临近区域(虚线以内的区域,具体定义见附录),A和B各自处于对方临近区域的部分用黑色表示。A的黑色部分的面积占总面积的比例就反映了A处于B临近区域的程度,反之亦然,这个比例越高越说明A和B应该合并。
|
图 2 目标之间临近度计算示意图 Fig. 2 Sketch map of computing method of close degree between two objects |
为此,本文将两个目标的临近度定义为:
| $ {r_{{\rm{A,B}}}} = {\rm{max}}({n_{\rm{A}}}/{N_{\rm{A}}},{n_{\rm{B}}}/{N_{\rm{B}}}) $ | (1) |
式中,NA和NB分别是目标A和目标B的总像素个数,nA和nB是目标A和B分别处于对方临近区域的像素个数。将本文定义的临近度应用于上述4个例子,结果显示在表 1的第六列。
为上述5种算子分别给定一个合适的阈值,得出对目标是否应该合并的判断,判断结果为应该合并的在表 1中用下划线加强显示。表 1显示只有第六列对4个实例的判断和人工判断完全一致。本文另外从2010年5—9月中挑选了86个人工容易判别的实例,统计得出应用上述5种算子进行判断的正确率分别为78%、85%、60%、78%和97%,其中每种客观方法临近度阈值选在使得每种方法出错次数最少的数值上(表 1底行)。可见采用本文提出的算子来定义临近度可以提高目标识别结果的合理性。
2.2 目标配对根据2.1节的算法从降水的预报场和观测场中识别出少数几个降水目标之后,接下来要将两个场的目标进行最优的配对。两个场中的目标可以一对一的配对,也将多个观测目标合并后再与一个预报目标配对,或者反过来,可以称之为一对多的配对,类似的还可以进行多对多的配对。若预报场和观测场各有n和m个初始目标,则完成一组配对的可能方式接近2n×2m种。定义目标之间的匹配度,通过计算每种配对方式的匹配度,找出其中的最大值,若它达到阈值则完成了一组目标的配对。如果n和m较大,2n×2m会是一个很大的数字,要将所有配对方式的匹配度都计算一遍代价太高。实际上需要多对多配对的情况并不常见,而且多对多的配对方式往往很复杂,即使人工也很难判断其配对结果是否合理。为此Gilleland等(2008) 提出目标配对中应该主要考虑一对一和一对多的配对方式,并提出了有效的计算步骤。但Gilleland等(2008) 的算法中采用距离的倒数作为对目标匹配度的定义,根据2.1节的讨论,这种算子只能考虑到位置因素,容易出现不合理的配对结果,为此本文给出了一种更为合理的匹配度定义如下:
| $ {C_{{\rm{A, B}}}} = \frac{{{n_{\rm{A}}} + {n_{\rm{B}}}}}{{{N_{\rm{A}}} + {N_{\rm{B}}}}} $ | (2) |
式中,方程右边的各个变量的含义和式(1) 中相同,式中分子部分为两个目标重合或临近的像素,分母为两个目标的总像素,两个目标位置、形状和尺度越匹配,CA,B的取值会越大。
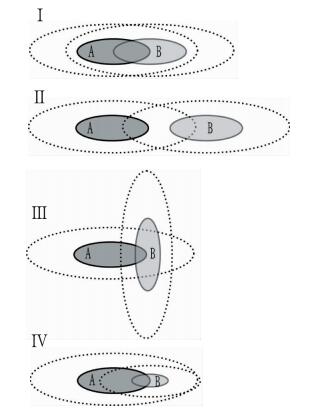
以示意图 3中的4个例子来说明式(2) 在计算匹配度时对目标的位置、形状和尺度3个因素的响应。图 3中A和B分别代表预报场和观测场的两个目标。例Ⅰ中A和B两个目标相距较近,互相完全处于对方的临近区域,因此匹配度为1。例Ⅱ中A和B的情形和例Ⅰ中相似,但两者相距更远,因此两者不完全处于对方的临近区域,匹配度比例Ⅰ小。例Ⅲ,A同B的中心位置的距离与例Ⅰ相同,但两者形状不一致,图中表现为主轴方向不一致,则两者也不能完全处于对方的临近区域,匹配度比例Ⅰ小。例Ⅳ,A同B的形状和中心位置的关系和例Ⅰ中相同,只是例Ⅳ中B的尺度明显比A小,虽然B完全处于A的临近区域,但A只有部分处于B的临近区域,因此匹配度也小于例Ⅰ的情况。由此可以看出式(2) 定义的匹配度能够综合反映两个目标的位置、形状和尺度的一致性。
|
图 3 目标的位置、面积和形状对匹配度的影响示意 Fig. 3 Response of match degree to the position, area and shape of two objects |
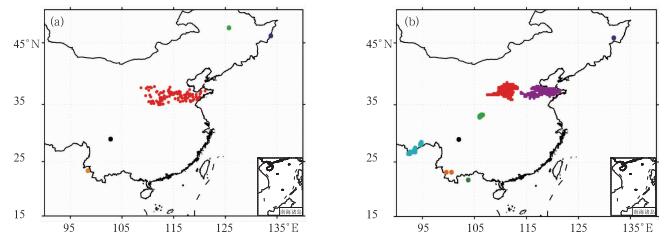
采用本文定义的匹配度,按Gilleland等(2008) 提出算法步骤来对目标进行配对。图 4显示了2011年7月3日08时24 h累积降水观测和对应的EC模式的24 h降水预报的目标初步识别的结果,对其进行目标配对,结果见图 5。本文以此为例来说明目标配对的具体步骤。
|
图 4 经过初步识别的观测(a)和预报(b)的降水目标 (不同的颜色代表不同的目标,(a)中蓝、红、黄、绿和黑色目标编号分别为1、2、3、4和5,(b)中蓝、红、桃红、青、黑、浅绿、黄和深绿编号分别为1、2、3、4、5、6、7和8) Fig. 4 Precipitation objects of observation (a) and forecasting (b) after initial identification (Different colors represent different objects. In (a), blue, red, yellow, green and black correspond to the objects of number 1, 2, 3, 4 and 5. In (b), blue, red, pink, cyan, black, light green, yellow and dark green correspond to the objects of number 1, 2, 3, 4, 5, 6, 7 and 8) |
|
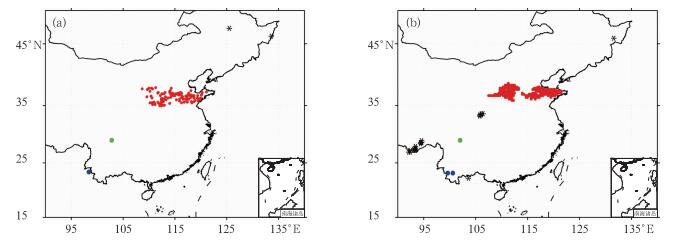
图 5 经过配对后的观测(a)和预报(b)的降水目标 (图中“*”代表的是未实现配对的目标,其他同一颜色的目标代表实现配对的一对预报和观测目标, 绿色、红色和蓝色分别对应表 3中第二、三和四行的目标) Fig. 5 The matched precipitation objects of observation (a) and forecasting (b) (The "*" represents the unmatched objects in (a) and (b), and one color represents a pair of matched objects. Green, red and blue respectively correspond to the objects in line 2, 3 and 4 in Table 3) |
步骤1,给观测场和预报场的目标进行编号,计算两个场的目标两两之间的匹配度,结果如表 2。
|
|
表 2 观测目标和预报目标之间的匹配度 Table 2 The match degrees of observed objects and predicted objects |
步骤2,对表 2中每一行从大到小排序。对于每个观测场的目标,用jk, k=1, 2, …, NB来标记和它匹配度排序为k的预报场目标。以表 2的第二个目标所在行为例,和第二个观测目标匹配度最高的是第三个预报目标,因此j1=3,匹配度排序第二的是第二个预报目标,因此j2=2。
步骤3,对于每个观测场目标,将与它匹配度最大的前k个预报目标合并,再计算合并后的目标与此观测目标的匹配度,结果如表 3。以表 3中第二个目标所在行第二列的元素为例,它表示的是第二个观测目标和第j1同第j2个(即第三个及第二个)预报目标的合并目标的匹配度。
|
|
表 3 观测目标和合并后的预报目标之间的匹配度 Table 3 The match degrees of observed objects and merged predicted objects |
步骤4,按步骤2和3的方式对纵向也进行排序、合并和匹配度的计算,结果如表 4。
|
|
表 4 合并后观测目标和预报目标之间的匹配度 Table 4 The match degrees of merged observed objects and predicted objects |
步骤5,找出表 2、表 3和表 4中所有数值的最大值Cmax,如果Cmax大于匹配度阈值,则它对应的预报场和观测场目标实现了配对。在此实例中第五个观测目标和第五个预报的匹配度为1,第二个观测目标和第二个同第三个预报目标的合并目标的匹配度为1,这两对目标的匹配度同为最大值,且都超过了阈值,实现了配对。将已经配对的目标剔除后重复步骤1至5,直到匹配度最大值Cmax小于阈值时终止算法。
根据式(2),如果第i个观测目标同所有预报目标匹配度都为0,则它同多个预报目标的合并目标的匹配度必然还是0,因此在步骤3中可以省略计算。如果第i个观测目标和对应的第jk个预报目标的匹配度为0,i和j1, …, ∪jk-1的匹配度一定小于i和j1, …, Vjk-1的匹配度,因为前者只在分母上有所增加而在分子上没有变化,此时也就可以省略计算表 3中第i行、第k列及之后的元素,正如表 3所示,同理表 4中亦可进行类似的简略。由此可见采用本文定义的匹配度进行目标配对,相比于Gilleland等(2008) 的算法中采用距离进行计算,不但结果更合理,而且计算量也得到很大的节省。在上述实例中,通过匹配算法实现的最终配对情况如表 5。
|
|
表 5 实现配对的观测和预报目标的编号和匹配度,以及未实现配对的观测和预报目标编号 Table 5 The numbers of matched, and unmatched objects of observation and forecasting and match degrees |
在完成目标匹配之后,就可以针对每一对已经配对好的目标进行检验。一个降水目标最基本的属性包括中心位置、主轴方向、主轴的特征长度、次轴的特征长度和覆盖面积等特征。
2.3.1 目标的中心位置采用矩阵X2×N=(x1, x2, …, xN)表示预报或观测目标的点集,其中矢量xk表示目标中第k个点的经纬度坐标。目标的中心位置为
| $ \mathit{\boldsymbol{\bar x}} = \frac{1}{N}\sum\limits_{k = 1}^N {{\mathit{\boldsymbol{x}}_k}} $ | (3) |
目标中每个点相对于中心的坐标为dk=xk-
对于格点形式的模式降水目标,其面积可以通过目标的格点数来确定,考虑到不同纬度上每个格点代表的面积不同,可以用如下方式计算
| $ {s_f} = \sum\limits_{i = 1}^N {d_f^2{\rm{cos}}{\varphi _i}} $ | (4) |
式中,N为降水目标的像素点数,df为格距(°),φi为第i个像素的纬度(弧度)。
对于分布散乱的观测降水目标的覆盖面积本文采用如下方法计算:首先用等经纬度网格将整个区域划分成n×m个小区域,网格的格距设为do,再通过式(5) 计算降水目标的覆盖面积
| $ {s_o} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {d_o^2{\rm{cos}}({\varphi _{i, j}}){r_{i, j}}} } $ | (5) |
式中, φi, j为第i行、第j列网格位置的纬度,式(5) 中
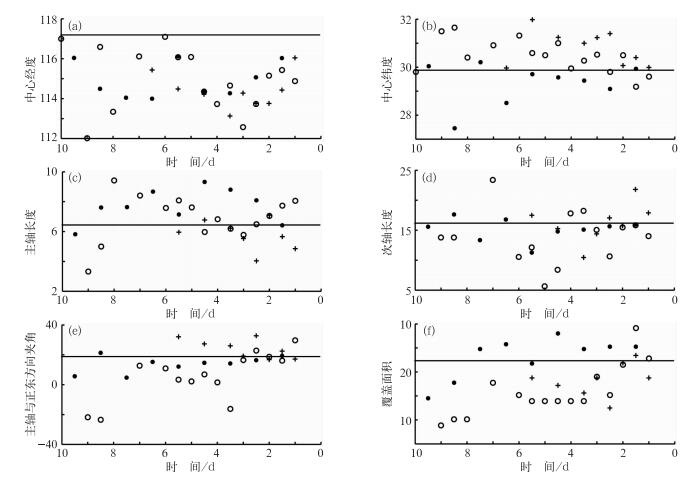
基于上述本文改进后的目标识别方法,依托国家气象中心实时预报数据库,本文进一步开发了可为主观预报提供模式检验和比对信息的产品(图 8),将降水目标的每一个属性显示在不同的子图中,而同一子图中同时显示了T639、ECMWF和日本3家主流业务数值模式各个时效对应预报目标的属性,图中水平直线代表观测目标的属性值。该产品不仅以简明的形式显示了降水目标各个属性的检验信息,由此可以方便地对模式预报与实况进行对比检验,同时还可以对多模式、不同时效的预报结果进行对比检验。
|
图 8 多模式多时效预报的降水目标的属性检验 (a)中心经度,(b)中心纬度,(c)主轴长度,(d)次轴长度,(e)主轴与正东方向夹角,(f)覆盖面积 (横线的纵坐标有对应观测降水目标的属性取值,“”、“。”和“+”分别对应T639、ECMWF和日本模式预报降水目标的属性取值) Fig. 8 Property verification of precipitation objects of multi models and multi-time forecast (a) central longitude, (b) central latitude, (c) length of principal axis, (d) length of secondary axis, (e) included angle of principal axis and east direction, (f) covering area ("", "." and "+" respectively correspond to T639, ECMWF and Japan models, and the horizontal line represents the value of the observed object) |
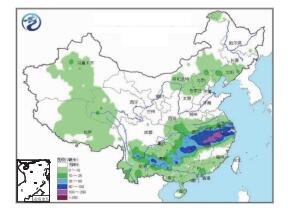
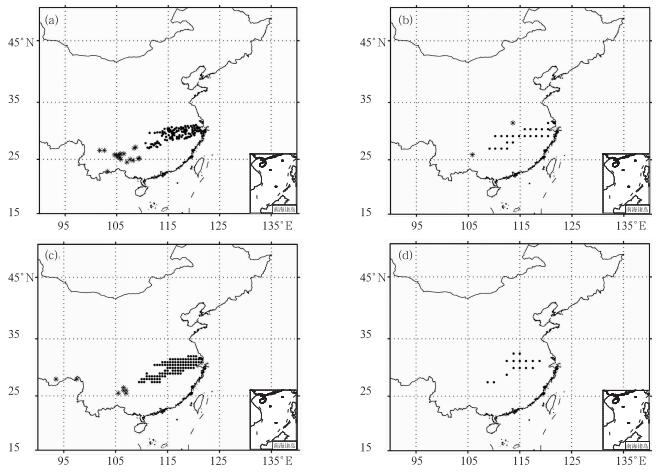
本文以2011年6月长江中下游地区旱涝急转事件中的6月13—15日第三次强降雨过程为例,给出了基于目标识别的降水量检验方法及产品的实际应用效果。第三次强降雨过程中以14日08时至15日08时日降雨强度最大(图 6),江南出现了大范围的区域性暴雨—大暴雨天气。本文对各个时效模式预报和观测的暴雨降水目标进行了识别和配对,其中36 h时效结果显示在图 7中,其他时效结果本文省略显示。图 8给出了对该暴雨区多模式降水预报检验结果。由图 8可见,各家模式对暴雨区的位置、范围、强度和轴向等属性的预报与实况存在着不同程度的偏差。
|
图 6 2011年6月14日08时至15日08时全国降水实况 Fig. 6 The observation of cumulative rainfall from 08:00 BT 14 to 08:00 BT 15 June 2011 |
|
图 7 2011年6月14日08时至15日08时累积降水的观测场(a)和T639(b)、ECMWF(c)和日本(d)模式预报场中50 mm的降水目标 (“*”点为未实现配对的目标,“.”为实现配对的目标) Fig. 7 Precipitation objects of observation (a) and T639 (b), ECMWF (c) and Japan (d) models from 08:00 BT 14 to 08:00 BT 15 June 2011 (The "." represents the matched objects and "*" represents the unmatched objects) |
(1) ECMWF模式各时效预报均未漏报该暴雨目标,而T639模式在156、180和228 h时效漏报了该降水目标,日本模式在96、120和144 h时效也出现了漏报。
(2) 中心纬度位置检验:各家模式预报的暴雨落区均系统性地偏西;对雨带中心纬度的预报则随着预报时效的临近逐渐向实况逼近,其中ECMWF模式预报结果在南北摆动中逐渐接近实况,预报时效在132 h内预报与实况暴雨区中心纬度位置差异小于1°,T639和日本模式的预报多较实况暴雨区偏北。
(3) 雨带的长宽和走向的检验:ECMWF模式预报的雨带长度系统性的偏大,而T639和日本模式预报的雨带长度误差大但无系统性规律;对于雨带宽度的预报,ECMWF模式明显好于T639模式和日本模式,T639模式预报的雨带整体偏窄,而其他两家模式无明显系统性偏差;对于雨带的走向,ECMWF模式预报各时效的预报和实况较为接近,T639模式预报的雨带倾角整体较实况小,即雨带更偏向呈东—西走向,而日本模式预报的雨带倾角较实况偏大,雨带更偏向呈东北—西南走向。
(4) 覆盖面积检验:ECMWF模式对暴雨区范围的预报在预报时效8~9 d偏小,1~7 d偏大,T639和日本模式的对暴雨区范围的预报整体较实况暴雨区偏小。
4 小结与讨论目前,天气预报业务和模式研究中常用的降水检验方法是TS评分等基于点对点的检验方法,与此同时,基于目标的检验方法正逐渐发展成型,但在业务上的应用还不多见。本文综合已有的研究,对基于目标的检验方法进行了系统地阐述,详细介绍了它的算法步骤,并对其中的关键算子进行了优化。
(1) 在目标识别的计算中,定义了一个能综合反映目标位置、面积和形状因素的临近度,使得目标识别的结果更加合理。
(2) 在目标配对的计算中,定义了一个能综合反映目标位置、面积和形状因素的匹配度,使得目标的配对更加合理,所需计算量也得到减少。
(3) 在目标检验的计算中,给出了降水目标的中心位置、长短轴大小和方向以及覆盖面积等属性的计算方法。
(4) 将本文改进的算法应用到对T639、ECMWF和日本模式降水场预报的检验中,提供了强降水雨带位置、形状和范围等属性的检验信息,以简明的图片产品同时实现了预报与观测、不同时效预报和多模式预报的对比检验。该产品已在国家气象中心开展试用,为业务预报提供定量的参考信息。
(5) 鉴于从单日降水检验得到的模式偏差的规律不具有普适性,今后我们将在本文上述研究工作的基础上,进一步开展对近年来大量强降水实例的检验分析,尝试从中找出模式的系统性偏差,为预报订正提供更有力的订正依据,也为寻找模式偏差的原因及改进模式提供参考依据。
附录目标的邻近区域的定义:
(1) 计算目标的主轴和次轴的特征长度(l1,l2)和特征方向(v1和v2)。
(2) 设定一个特征尺度D0,定义反映降水目标形状的属性:
| $ \gamma = {\rm{max}}\left[ {\frac{{{\rm{max}}({l_2}, {D_0})}}{{{\rm{max}}({l_1}, {D_0})}}, 0.5} \right] $ |
(3) 点到目标A中第i个像素(ai)的距离定义为:
| $ {d_{x, {a_i}}} = {[\gamma (\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{a}}_i})\cdot{\mathit{\boldsymbol{v}}_1}]^2} + {[(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{a}}_i})\cdot{\mathit{\boldsymbol{v}}_2}]^2} $ |
(4) 点到目标A的距离定义为:
| $ {d_{x\_A}} = {\rm{min}}({d_{x, {a_i}}}, {\rm{ }}i = 1, n) $ |
(5) 邻近区域定义为所有到目标距离小于D0的区域。
根据上面的定义,当目标的尺度小于D0时,其邻近区域是均匀的往四周延伸。如果目标尺度大于D0且呈团状分布,其邻近区域也是较均匀的向四周延伸。如果目标尺度大于D0,且呈狭长带状,则其邻近区域沿着主轴的方向要延伸的更远,但最多不超过两倍D0的距离。
管成功, 陈起英, 佟华, 等, 2008. T639L60全球中期预报系统预报试验和性能评估[J]. 气象, 34(6): 11-16. DOI:10.7519/j.issn.1000-0526.2008.06.002 |
周慧, 崔应杰, 胡江凯, 等, 2010. T639模式对2008年长江流域重大灾害性降水天气过程预报性能的检验分析[J]. 气象, 36(9): 60-67. DOI:10.7519/j.issn.1000-0526.2010.09.010 |
Davis C A, Brown B G, Bullock R G, 2006a. Object-based verification of precipitation forecasts.Part Ⅰ: Methodology and application to mesoscale rain areas. [J]. Mon Wea Rev, 134(7): 1772-1784. DOI:10.1175/MWR3145.1 |
Davis C A, Brown B G, Bullock R G, 2006b. Object-based verification of precipitation forecasts.Part Ⅱ: Application to convective rain system. [J]. Mon Wea Rev, 134(7): 1785-1795. DOI:10.1175/MWR3146.1 |
Davis C A, Brown B G, Bullock R G, et al, 2009. The method for object-based diagnostic evaluation (MODE) applied to WRF forecasts from the 2005 spring program[J]. Wea Forecasting, 24(5): 1252-1267. DOI:10.1175/2009WAF2222241.1 |
Gilleland E, Lee T C M, Gotway J H, et al, 2008. Computationally efficient spatial forecast verification using Baddeley's delta image metric[J]. Mon Wea Rev, 136(5): 1747-1757. DOI:10.1175/2007MWR2274.1 |
Jolliffe I T, Stephenson D B, 2003. Forecast Verification.A Practitioner's Guide in Atmospheric Science.[M].
Sigapre: Wiley.
|
Lack S, Limpert G L, Fox N I, 2010. An object-oriented multiscale verification scheme[J]. Wea Forecasting, 25: 79-92. DOI:10.1175/2009WAF2222245.1 |
Marzban C, Sandgathe S, 2006. Cluster analysis for verification of precipitation fields[J]. Wea Forecasting, 21: 824-838. DOI:10.1175/WAF948.1 |
Nachamkin J E, 2004. Mesoscale verification using meteorological composites[J]. Mon Wea Rev, 132: 941-955. DOI:10.1175/1520-0493(2004)132<0941:MVUMC>2.0.CO;2 |
Venugopal V, Basu S, Foufoula-Georgiou E, 2005. A new metric for comparing precipitation patterns with an application to ensemble forecasts[J]. J Geophys Res, 111(8): 1-11. |
 2013, Vol. 39
2013, Vol. 39 