引言

为体现大气的混沌特性及数值预报中模式误差、初值误差等带来的不确定性, Epstein(1969)提出了动力随机预报, Leith(1974)提出了“蒙特卡罗"预报(Monte Carlo forecast), 自此集合数值预报技术开始走向实际应用。20世纪90年代初美国国家环境预报中心(NCEP)(Zoltan et al, 1993)和欧洲中期天气预报中心(ECMWF)(Molteni et al, 1996)先后建立了自己的全球中期集合预报业务系统, 其他国家也相继建立了自己的集合预报业务系统(Young et al, 2008)。我国在1998年建立了基于T106L19全球模式的中期集合预报系统, 并于2001年投入业务使用, 2006年底建立了基于T213L31全球模式的中期集合预报系统。经过近十几年的努力, 我国全球集合预报技术在理论研究和业务实践上都获得了一定的进展(矫梅燕, 2010; 陈静等, 2002; 杜钧等, 2010)。

集合预报扰动方法是集合预报技术的核心问题, 其本质是通过分析数值预报不确定性来源, 采用合理的扰动方法, 对数值预报初值和模式自身的不确定性进行定量描述和数学处理。由于大气运动非线性混沌特性(Lorenz, 1963), 初值的微小误差对未来的预报结果影响很大, 使得数值预报结果具有不确定性, 因此初值扰动集合预报技术具有坚实的理论基础, 针对初值扰动技术的研究更加成熟, 国际上主流的初值扰动方法有奇异向量法、增长模繁殖法、卡尔曼滤波法等(Hoffman et al, 1983; Dalcher et al, 1988; Murphy, 1990; Houtekamer et al, 1996; Buizza et al, 1999; Alberto et al, 2004)。

此外, 模式自身的不确定性也是数值预报不确定性的一个重要因素, 尤其是次网格尺度物理过程参数化造成的预报不确定性。研究表明仅采用初值扰动方法构建的集合预报系统离散度偏小(Houtekamer et al, 1996; Buizza et al, 1999; Alberto et al, 2004), 同时包含初值扰动和模式扰动的集合预报能更好地表现数值预报的不确定性(David et al, 2000; Joo et al, 2008)。因此, 模式扰动方法是集合预报扰动技术的重要组成部分, 目前多个国家已经在集合预报系统中引入了模式扰动方法, 结果表明集合预报离散度和预报技巧都有一定的提高。国际上模式扰动主要采用以下三种方法: (1) 使用不同的物理过程参数化方案组合来模拟不同的物理过程参数化方案产生的不确定性(Houtekamer et al, 1996); (2) 采用多模式的方法模拟不同模式系统的不确定性(Harrison, 1999; 严明良等, 2009); (3) 对模式每个积分步长产生倾向项上加入随机扰动项, 通常是对与中小尺度相关的物理过程产生的倾向项进行随机扰动, 体现中小尺度预报不确定性, 简称为随机物理过程扰动方法(Buizza et al, 1999)。

随机物理过程扰动方法是模式扰动技术的重要方向。ECMWF的Buizza等(1999)提出在集合预报系统的模式参数化物理过程倾向项上加入随机扰动, 其依据是物理过程参数化过程所造成的随机误差在不同参数化方案之间是相关的, 并且在模式的空间和时间尺度上也存在着一定的相关, 这种方法假设物理参数化倾向项作用越大, 随机误差的值就越大。1998年10月此方案应用于ECMWF集合预报业务系统中, 增加了集合预报成员的离散度, 提高了概率预报的技巧。2004年ECMWF又引入随机动能散射方案(Shutts, 2004), 继续改进了集合预报的性能。加拿大全球集合预报系统中模式扰动采用的是随机物理过程扰动和随机动能散射方案相结合的类似方案(Charron et al, 2010), NCEP全球及区域集合预报系统采用对总物理过程倾向项进行随机扰动。

国内集合预报模式扰动方法研究多采用不同物理过程参数化方案随机组合的方法, 并多用于中尺度模式的研究(谭燕等, 2008; 陈静等, 2003; 王建捷等, 2005)。全球模式随机物理过程扰动方法的研究相对较少, 任志杰等(2011)基于我国T213全球中期预报模式开展了模式随机扰动方法的研究, 她通过对模式物理过程和动力过程的总倾向项进行随机扰动, 综合考虑模式动力过程和次网格尺度物理过程参数化的不确定性, 改善了增长模繁殖法(BGM)的多初值集合预报效果, 而动力过程和物理过程分别的影响, 特别是物理过程参数化方案对集合预报的影响涉及较少。本文通过设计仅对参数化物理过程倾向项进行随机扰动的试验方案, 对比分析这两种方案优劣, 开展集合预报试验, 更加深入地认识物理过程随机扰动方案对集合预报系统的影响和扰动传播机理, 为发展集合预报技术提供科学依据。

1 两种模式随机扰动方案设计

本文基于CMA T213全球集合预报系统, 参考Buizza等(1999)和任志杰等(2011)的方案, 设计两种模式扰动试验方案, 第一种方案对参数化物理过程倾向项和动力过程倾向项之和, 以下简称随机总倾向扰动方案(Stochastic Total tendency Perturbation Scheme, STPS)进行随机扰动; 第二种方案仅对参数化物理过程产生的倾向项进行随机扰动, 以下简称随机物理扰动方案(Stochastic Physics Perturbation Scheme, SPPS), 下面对STPS和SPPS这两种方案进行详细介绍。

设有初始扰动条件下模式积分:

${e_j}\left( t \right) = \smallint _{t = 0}^t\left\{ {A({e_j},{\rm{ }}t) + P({e_j},{\rm{ }}t)} \right\}{\rm{d}}t$

(1)

其中, e_j表示集合成员, 当j=0时表示控制预报。

积分倾向项可分解为:

$\frac{{\partial {e_j}}}{{\partial t}} = A({e_j},t) + P({e_j},t)$

(2)

式中, A(e_j, t)代表非参数化过程(动力过程)积分倾向项, P(e_j, t)代表参数化的物理过程积分倾向项。

STPS方案对参数化的物理过程积分倾向项P(e_j, t)和非参数化过程积分倾向项A(e_j, t)产生的总倾向项进行随机扰动

$\begin{array}{l} e_j^{{\rm{STPS}}}\left( t \right) = \smallint _{t = 0}^t\{ {r_j}\left( {x,y,z,t} \right)A({e_j},t) + \\ \quad \quad \quad \quad {r_j}\left( {x,y,z,t} \right)P({e_j},t)\} {\rm{d}}t \end{array}$

(3)

SPPS方案仅对参数化的物理过程积分倾向项P(e_j, t)进行随机扰动

${e^{{\rm{SPPS}}}}_j\left( t \right) = \smallint _{t = 0}^t\left\{ {A({e_j},t) + {r_j}\left( {x,y,z,t} \right)P({e_j},t)} \right\}{\rm{d}}t$

(4)

其中, r_j(x, y, z, t)表示随机数, r_j(x, y, z, t)选取[0.5, 1.5]均匀分布的随机数。P(e_j, t)为T213集合预报模式的辐射传输、湍流混合、次网格尺度地形拖曳、湿对流和积云对流等参数化物理过程产生的积分倾向项。物理过程随机扰动的实现方法为在模式每个积分步长(15 min)、每个格点上的积分倾向项乘上[0.5~1.5]内均匀分布的随机数, 实现对模式积分变量温度、比湿、U分量风、V分量风积分倾向项的随机扰动。由式(3) 和(4) 可见, STPS方案和SPPS方案随机扰动的因子有所不同, 前者是对非参数化积分倾向与参数化的物理过程积分倾向项之和, 即总倾向项进行随机扰动, 后者是对参数化的物理过程产生的倾向项进行随机扰动。

2 集合预报试验设计 2.1 T213全球数值集合预报系统简介

T213L31数值预报业务系统是国家气象中心数值预报室在引进的欧洲中期天气预报中心IFS(Integrated Forecasting System)模式框架基础上, 经过移植改造和自行开发与其匹配的最优插值(SSI)资料分析同化方案、模式后处理方案、大规模并行机环境下的自动化运行流程及作业监控方案等, 所形成的我国新一代全球中期数值预报业务系统(胡江凯, 2005)。

T213模式系统包含一整套比较先进的物理过程, 包括(Morcrett, 1990)长波辐射方案, (Fouquart et al, 1980)短波辐射方案, 对可分辨山脉的描述采用平均地形方法, 次网格地形拖曳参数化方案(Lott et al, 1996), 湍流扩散方案(Louis, 1979), 云方案(Tiedtke, 1993)和陆面过程(Vitesbo, et al, 1995), 采用Tiedtke(1989)的质量通量方案描述了各种类型的对流(陈起英等, 2004)。我国T213全球集合预报系统是基于T213全球中期数值预报系统建成。采用增长模繁殖法(Breeding Vector)产生14个初始扰动集合, 目前无模式扰动。

2.2 STPS和SPPS方案集合预报试验设计

试验时段为2008年7月20—31日, 总计12天。积分启动时间为每日12:00UTC, 做10天预报, 积分间隔24 h输出一次结果, 扰动初值来自T213集合预报系统增长模繁殖法(BGM)方案。

本文在试验时段内进行三组集合预报试验, 试验细节见表 1, 其中无模式扰动试验未加入模式扰动, SPPS试验和STPS试验分别采用SPPS扰动方案和STPS扰动方案。

2.3 集合预报检验方法

检验方法采用常规概率预报检验方法:离散度(SPREAD)检验, 均方根误差(RMSE)检验, Brier评分(BS)和连续分级概率评分(CRPS)。离散度是衡量集合成员围绕集合平均的平均变化幅度, 即集合预报成员之间的发散程度, 成员之间的发散程度在一定范围内越大越能体现预报的不确定性; 均方根误差检验(RMSE)是比较集合预报平均与相应分析场之间差异, 衡量平均预报误差大小; Brier评分用于检验集合预报准确性, BS值越小表明集合预报准确性越高; 连续分级概率评分(CRPS)也是用于检验集合预报准确性, CRPS值越小表明集合预报准确性越高。下面是以上检验方法的数学计算公式

$\begin{array}{l} SPREAD = \frac{1}{{m \times n}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\left\{ {\frac{1}{N}} \right.} } \sum\limits_{mem = 1}^N {[{f_{mem}}\left( {i,{\rm{ }}j} \right)} \\ \quad \quad \quad \quad \quad {\left. { - \overline {f\left( {i,{\rm{ }}j} \right)} {]^2}} \right\}^{\frac{1}{2}}} \end{array}$

(5)

其中, N表示成员数, f_mem(i, j)表示预报场, f(i, j)为集合平均, m和n分别为经向和纬向格点数。

$RMSE = \sqrt {\frac{1}{{m \times n}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{{\left[ {F\left( {i,{\rm{ }}j} \right) - O\left( {i,{\rm{ }}j} \right)} \right]}^2}} } } $

(6)

其中, F(i, j)是集合预报场, O(i, j)是相应的分析场。

$BS = \frac{1}{N}\sum\limits_{n = 1}^N {{{({P_n} - {O_n})}^2}} $

(7)

其中, N为特定二分类事件的样本总数(是对空间和检验时间段的累积), P_n是第n个样本的被检验事件的集合预报概率, 其值为0~1, O_n是第n个样本的被检验事件的观测频率, 如果观测到检验事件, O_n的值为1, 否则其值为零。

$CRPS(P,{\rm{ }}{x_a}) = \smallint _{ - \infty }^\infty {[P\left( x \right) - {P_a}\left( x \right)]^2}{\rm{d}}x$

(8)

其中, P(x)为概率预报累计分布, P_a(x)为观测真值累计分布。

3 集合预报效果检验与分析 3.1 大气运动特征变量检验

选取850 hPa温度场(T850)、500 hPa位势高度场(Z500) 和250 hPa纬向风速(U250) 分别代表大气低层、中层和高层运动特征变量进行集合预报检验, 为了分析不同区域的预报效果, 将检验分为四个区域进行:北半球热带外地区(20°~90°N, 简称NH)、南半球热带外地区(20°~90°S, 简称SH)、热带地区(20°N~20°S, 简称EQ)、东亚地区(15°~65°N、70°~145°E, 简称EA)。

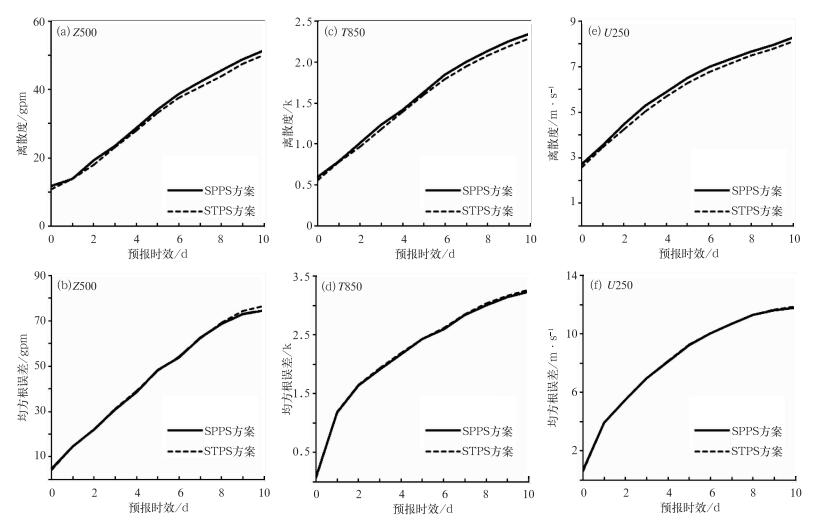
图 1是SPPS和STPS试验在北半球热带外地区的离散度和均方根误差检验, 由图 1a可知, 在10天的预报时效内, SPPS试验的Z500离散度大于STPS试验(图 1a), 在积分中后期尤为显著; 两组试验的Z500 RMSE在积分7 d之前差别不大, 积分7 d后SPPS试验的RMSE明显小于STPS试验(图 1b)。SPPS试验的T850 SPREAD整体大于STPS试验的结果(图 1c); 从T850 RMSE检验可见(图 1d), SPPS和STPS两组试验RMSE差别不大, 但前者RMSE略小。U250的SPREAD和RMSE演变特征与T850类似, 不再赘述(图 1e和1f)。SPPS和STPS试验在南半球热带外地区的SPREAD和RMSE检验结果与北半球热带外地区类似; 在热带和东亚地区, T850、Z500和U250的SPREAD和RMSE检验结果基本一致。

由上可知, SPPS随机扰动方案较STPS随机扰动方案的集合预报技巧获得一定程度的提高, 集合成员在南、北半球热带外地区的离散度略大, 均方根误差略小, 但热带和东亚地区的离散度和均方根误差差别不大。

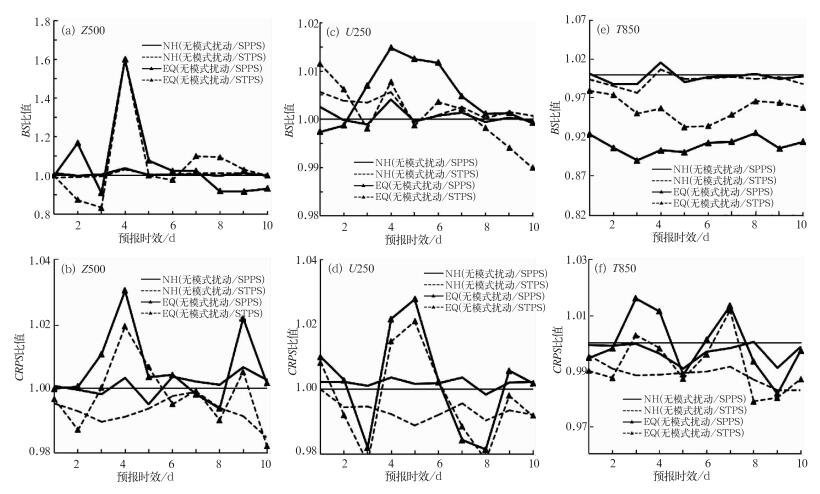
图 2给出的是无模式扰动试验与SPPS试验、无模式扰动试验与STPS试验的Z500、U250和T850在北半球热带外地区和热带地区的Brier评分(BS)比值和CRPS比值。BS是检验集合预报准确性的评分, BS值越小表明集合预报准确性越高,图中SPPS试验的BS小于无模式扰动试验时, 二者比值大于1, 即SPPS试验的概率预报准确性高于无模式扰动。连续分级概率评分(CRPS)也是一种检验集合概率预报准确性的评分, 值越小表明集合预报准确性越高。由图可知, SPPS试验和STPS试验的Z500 BS在北半球热带外地区较为一致(图 2a), 且都优于无模式扰动试验的结果, 在预报时效第4天两个试验的BS改进最显著; 在热带地区, SPPS试验的Z500 BS在前7天的预报时效内较无模式扰动试验有很大的改进, 其中第4天改进最明显, 积分7天后, 评分逐渐变差, STPS试验的Z500 BS改进和变差的时效各占一半。图 2c中SPPS试验的U250 BS在上述两个区域的结果都优于无模式扰动试验, 且热带地区的改进要大于北半球热带外地区; STPS试验的U250 BS在北半球热带外地区优于无模式扰动试验和SPPS试验的结果, 但在热带地区, 其BS在积分后期逐渐变差。SPPS试验和STPS试验的T850 BS除在北半球个别时效有改进之外其他结果都略差(图 2e)。

SPPS试验东亚地区的Z500和U250的BS改进次于北半球热带外地区和热带地区, 南半球热带外地区的BS改进不显著, STPS试验在南半球热带外地区和东亚地区的Z500和U250的BS都比无模式扰动试验略差, 两组试验的T850 BS在南半球热带外地区和东亚地区都没有获得改进(图略)。

图 2b中, 在北半球热带外地区, SPPS试验的Z500 CRPS在积分后期改进明显, STPS试验的Z500 CRPS略变差; 在热带地区, SPPS试验的Z500 CRPS除预报第7和8天外, 其他时效的CRPS均得到改进, STPS试验的Z500 CRPS除第3、4和第9天预报有改进外, 其他时效的评分略差。图 2d中, 在北半球热带外地区, SPPS试验的U250 CRPS在各个时效都有改进, STPS试验的U250 CRPS在各个时效略差; 在热带地区, 除了预报第3、7和8天的CRPS变差之外, 其他时效的SPPS试验的U250 CRPS均有改进, STPS试验的U250 CRPS除个别时效变优之外, 其他时效评分略差。SPPS试验和STPS试验的T850 CRPS除在热带地区个别时效有改进之外其他结果都略差(图 2f), 但前者优于后者。

在南半球热带外地区和东亚地区, SPPS试验、STPS试验的Z500、U250和T850的CRPS与BS分析结果类似(图略)。

总体上看, 集合预报模式加入SPPS的随机物理过程扰动方案后, 概率预报性能较无模式扰动和STPS方案在不同程度上得到提高, 其中北半球热带外地区和热带地区的500 hPa高度和250 hPa风的概率预报改进最为明显, 东亚地区次之, 南半球基本没有改进。

3.2 随机物理扰动方案(SPPS)典型个例降水预报检验

降水量是日常预报中非常受人关注的预报要素, 其预报技巧是检验模式预报效果的一个重要的指标, 从3.1中可知, 随机物理扰动方案(SPPS)可以有效地提高南北半球集合成员的离散度, 减小积分后期的均方根误差, 在一定程度上提高概率预报性能。在这节中, 我们将从试验时段中随机选取2008年7月22日20时至2008年7月23日20时的降水个例, 详细分析SPPS方案对降水量预报的影响及检验分析。

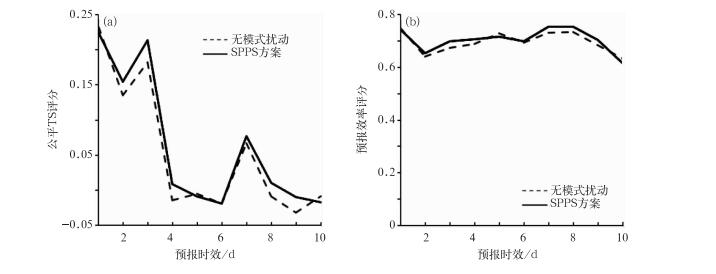
图 3是2008年7月23日20时的24 h累计降水实况及SPPS试验和无模式扰动试验累计降水集合预报平均图。从降水实况图可见(图 3a), 主降水带位于山东、江苏、河南南部、安徽北部、湖北中部、湖南北部和广西北部及云南南部地区。最大降水中心位于山东和江苏两省的交界处, 最大日降水量达100 mm以上。图 3b和3c分别为2008年7月23日12:00 UTC无模式扰动试验与SPPS试验的24 h累计降水集合平均结果, 可以看到两个试验的主降水落区与实况基本一致, 尽管最大降水中心值偏弱, 未能报出在山东与江苏两省交界处的100 mm以上降水中心, 但从SPPS试验与无模式扰动试验的集合平均差值发现(图 3d), 在实况出现暴雨的区域内, SPPS试验集合平均预报要强于无模式扰动试验的集合平均预报, 最大差值达15~20 mm, 可见SPPS试验的降水量预报更加接近实况。图 4是模式预报的中雨公平TS评分和预报效率评分。图 4表明SPPS试验的中雨公平TS评分和预报效率整体上优于无模式扰动试验的结果。SPPS试验的大雨、暴雨的公平TS评分和预报效率评分结果同样优于无模式扰动试验(图略)。

表 2为无模式扰动和SPPS两组集合预报试验的24 h分级降水预报相对作用特征曲线(ROC)面积(AROC) ROC代表的是事件预报的命中率和假警报率的相对比较关系, ROC曲线面积越大(越接近1), 说明命中率越高, 预报越好, 反之亦然。从表中可知, 小雨、中雨和大雨3个降水分级的ROC面积, SPPS试验的结果都大于无模式扰动试验, 说明SPPS方案改善了无模式扰动模式的降水预报技巧。

综上所述, T213集合预报模式加入随机物理扰动方案(SPPS)后, 强降水中心强度值有所增加, 中雨以上量级的集合预报降水ETS评分提高, 降水概率预报技巧也有明显的改进。

4 随机物理扰动方案(SPPS)的扰动分析

上面对两种模式随机扰动方案集合预报结果进行了检验评估, 结果表明SPPS方案的集合预报技巧和预报准确性优于STPS方案和无模式扰动方案。下面将重点分析SPPS方案的扰动特征和扰动能量的传播机制。

4.1 SPPS扰动特征分析及其与STPS的扰动特征比较

为了分析两种模式随机扰动对预报场的影响, 我们设计了离差试验方案(见表 3), 表 3中3组试验的预报结果作为试验对象, 积分时段为2008年7月20—31日, 共12 d。预报时效为1~10 d。定义绝对离差:S_{var, 2}(x, y, z, t), 以衡量模式随机扰动对预报变量的影响。

$\begin{array}{*{20}{l}} {{S_{{\rm{var, 2}}}}\left( {x,{\rm{ }}y,{\rm{ }}z,{\rm{ }}t} \right) = \frac{1}{n}\sum\limits_{st = 1}^n {{\rm{|va}}{{\rm{r}}_{\rm{1}}}} \left( {x,{\rm{ }}y,{\rm{ }}z,{\rm{ }}t,{\rm{ }}st} \right) - }\\ {\quad \quad \quad \quad \quad \quad \quad {\rm{va}}{{\rm{r}}_2}\left( {x,{\rm{ }}y,{\rm{ }}z,{\rm{ }}t,{\rm{ }}st} \right)|} \end{array}$

(9)

其中, var选取3组试验预报变量, var下标为试验号, var中变量t表预报时效, st表示起报时间。本文选用个例为12 d, 即n取12。

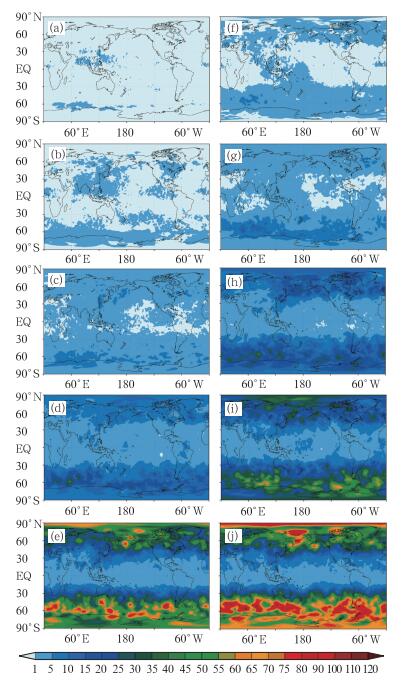
图 5为500 hPa位势高度场(Z500) 的绝对离差。图 5a~5e为TEST2-SPPS试验的Z500绝对离差S_{(z500, 2)}, 图 5f~5j为TEST3-STPS试验的Z500绝对离差S_{(z500, 3)}。

$\begin{array}{l} {S_{z500,{\rm{ }}2}}\left( {x,{\rm{ }}y,{\rm{ }}z,{\rm{ }}t} \right) = \frac{1}{{12}}\sum\limits_{st = 1}^{12} {|Z{{500}_1}} \left( {x,{\rm{ }}y,{\rm{ }}z,{\rm{ }}t,{\rm{ }}st} \right) - \\ \quad \quad \quad \quad \quad \quad \quad \quad Z{500_2}\left( {x,{\rm{ }}y,{\rm{ }}z,{\rm{ }}t,{\rm{ }}st} \right)| \end{array}$

(10)

$\begin{array}{l} {S_{z500,{\rm{ }}3}}\left( {x,{\rm{ }}y,{\rm{ }}z,{\rm{ }}t} \right) = \frac{1}{{12}}\sum\limits_{st = 1}^{12} {|Z{{500}_1}} \left( {x,{\rm{ }}y,{\rm{ }}z,{\rm{ }}t,{\rm{ }}st} \right) - \\ \quad \quad \quad \quad \quad \quad \quad \quad Z{500_3}\left( {x,{\rm{ }}y,{\rm{ }}z,{\rm{ }}t,{\rm{ }}st} \right)| \end{array}$

(11)

分析两组试验的绝对离差演变图, 总体上看, 随着积分时间的增加, 两组试验的Z500绝对离差的大小和范围都在不断地增大, 中高纬地区的绝对离差值大于热带地区, 南半球绝对离差值大于北半球, 至240 h积分时间, 热带地区离差值平均小于5 gpm, 北半球中高纬地区绝对离差值大部分在40~45 gpm以上, 南半球中高纬地区离差值平均为80~90 gpm; 两组试验的Z500绝对离差值各个时效在南半球表现得更敏感。其原因可能有两点:一是T213模式在南半球的预报技巧偏低; 二是南半球海洋面积大, 表现出更大的预报不确定性和高敏感性(任志杰等, 2011)。

值得关注的是两组试验绝对离差分布演变存在较大的差异。在积分前期, TEST2-SPPS试验的24 h绝对离差大值区主要集中在0°~30°N、60°~150°E的南亚和东南亚地区及南半球部分地区, 绝对离差值达5 gpm, 其他区域则不明显, 而TEST3-STPS试验24 h绝对离差值覆盖面更广并主要集中在中高纬地区, 绝对离差值也达到5 gpm, 随着积分时间的增加, TEST2-SPPS方案的离差大值区逐渐扩展到其他区域, 至240 h预报离差分布形态与TEST3-STPS方案趋于一致。TEST3-STPS试验的绝对离差值迅速地增大, 积分后期尤为明显, 在中高纬地区, TEST3-STPS试验绝对离差值增长速度比TEST2-SPPS试验大1~2倍, 绝对值为5~15 gpm, 至240 h, 绝对离差值最大达120 gpm以上, 而TEST2-SPPS试验为60~90 gpm。

分析产生上述差异的原因, 主要是因为SPPS方案只扰动了次网格尺度物理过程计算产生的积分倾向项, 因此对启动次网格物理过程计算的那些区域, 随机扰动的影响更为明显, 其他区域则没有影响。试验时段为7月, 正是东亚和南亚夏季风盛行期, 存在很强的经向垂直环流, 季风暖湿气流强盛, 对流不稳定能量充足(朱乾根等, 2000), 积分初期次网格物理过程随机扰动的影响在这个区域比其他地区更为显著, 离差值明显大于其他区域, 而STPS方案扰动的是总倾向项, 中高纬地区以斜压不稳定为主, 动力过程产生的倾向项随机扰动的影响会更明显, 因此STPS方案离差值主要集中在中高纬地区。可见SPPS方案可以反映模式次网格物理过程参数化的不确定性。

此外, 对850 hPa温度(T850)、250 hPa纬向风速(U250) 的12 d平均绝对离差也进行了对比分析(图略), 结果显示, T850、U250热带区域和中高纬区域的绝对离差值差异减小, 其他特征与500 hPa高度场类似, 在此不再赘述。

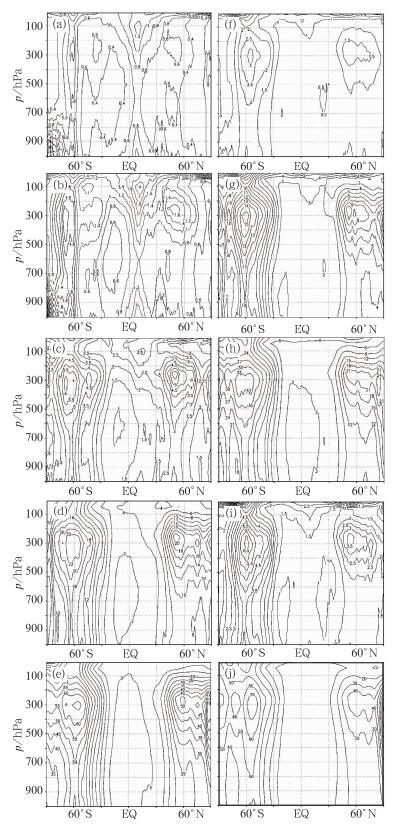
图 6为位势高度的绝对离差经向剖面图。图 6a~6e为TEST2-SPPS试验的位势高度绝对离差S_{(z, 2)}, 图 6f~6j为TEST3-STPS试验的位势高度绝对离差S_{(z, 3)}。由图可见, 积分24~48 h, 两组试验的位势高度绝对离差经向剖面存在明显差异, S_{(z, 2)}存在两个大值中心, 分别位于南半球高纬地区低层和热带地区的高层, 其中热带区域高层绝对离差值超过1.5 gpm, 其他区域分布较均匀, 而S_{(z, 3)}主要集中在南北半球中高纬地区的中高层, 其值在经向和垂直向上分布不均匀, 两个大值中心分别位于60°S和60°N的300 hPa高度附近, 中心最大值超过3和1.5 gpm, 离差绝对值远大于S_{(z, 2)}。随着积分时效的增长, 两组试验的绝对离差值不断增加, 积分96 h后, 两组试验热带地区的绝对离差值增加缓慢, 中高纬地区的绝对离差值迅速增加, 但在相同时效同一区域内, S_{(z, 2)}比S_{(z, 3)}小3~10 gpm。积分168 h后, 二者的绝对离差结构和量级趋于一致。

上述分析结果表明, 无论是水平方向还是垂直方向, 模式预报变量对两种模式随机扰动方案都非常敏感, 但仅扰动参数化物理过程的随机物理过程扰动方案(SPPS)对预报变量的影响较随机总倾向扰动方案(STPS)更加稳定, 更能合理表现模式物理过程的不确定性。

4.2 随机物理过程扰动方案(SPPS)的扰动场水平变化特征

为进一步分析SPPS方案对预报变量的水平方向影响特征, 对TEST2-SPPS试验各个时效的绝对离差值进行纬向平均, 且为了略去各个纬度上扰动值随预报时效增长的因素, 更清晰地分析扰动大值中心随预报时效的传播, 对纬向平均的离差值进行权重分析(公式12),

$\overline {{\rm{va}}{{\rm{r}}_{{\rm{权重}}}}\left( j \right) } = \frac{{\overline {{\rm{var}}\left( j \right)} - \frac{1}{N}\sum\limits_{j = 0}^{N = n} {\overline {{\rm{var}}\left( j \right)} } }}{{\frac{1}{N}\sum\limits_{j = 0}^{N = n} {\overline {{\rm{var}}\left( j \right)} } }}$

(12)

其中, j为经向格点, n为经向格点总数。var(j)为纬向平均离差值。

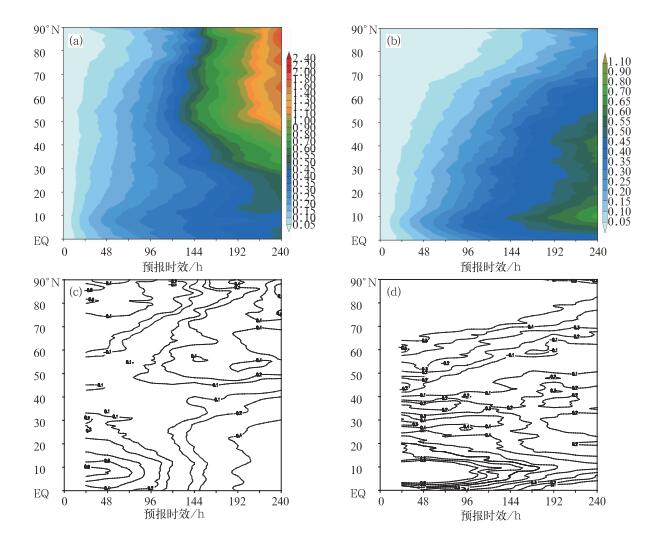
图 7是500 hPa温度场绝对离差[S_{(T500, 2)}]和500 hPa比湿q的绝对离差[S_{(q500, 2)}]的纬向平均和纬向平均权重的演变图。从图 7a中可以看出, 随着积分时间的增加, 各纬度上的S_{(T500, 2)}不断增加, 96 h积分前, 低纬地区的S_{(T500, 2)}增长速度大于中高纬地区; 96 h积分后, 中高纬地区的S_{(T500, 2)}迅速增大。积分240 h, 80°~ 90°N之间的S_{(T500, 2)}最大, 平均为2.4 K。S_{(T500, 2)}有着随积分时间的增长从低纬向中高纬发展的趋势。图 7c是S_{(T500, 2)}的纬向平均权重, 图中正值区是各个预报时效内S_{(T500, 2)}大值中心所在的纬度, 从这张图中可以看出, 随着预报时效的增加, S_{(T500, 2)}大值区有从低纬向中高纬传播的趋势。另外, 我们分别对低层(850 hPa)、中层(500 hPa)和高层(250 hPa)的高度场、温度场、风场这些变量的绝对离差进行了纬向平均, 得出的结论与S_{(T500, 2)}类似, 在此不再赘述。由图 7b和7d可知, S_{(q500, 2)}的纬向平均特征与风场、温度场和高度场的特征不同, 在低纬和中纬地区, S_{(q500, 2)}增加的速度一直大于高纬地区, 绝对离差大值区一直集中在中低纬地区。主要原因是水汽集中分布在中低层的中低纬地区, 比湿q的绝对离差分布从侧面说明了随机物理扰动方案(SPPS)的合理性。

4.3 随机物理扰动方案(SPPS)的波谱能量分析

为进一步分析物理过程参数化的随机扰动对T213中期预报模式预报结果产生的影响, 本节将对表 3中控制预报试验和TEST2-SPPS试验的总能量偏差(DTE)进行离散的傅里叶变换(DFT), 分解得到1~213个波的总能量偏差。总能量DTE的定义(Zhang et al, 2003)如式(13) 所示,

$DTE = \frac{1}{2}\sum {[{{(U{\prime _{i,{\rm{ }}j,{\rm{ }}k}})}^2} + {{(V{\prime _{i,{\rm{ }}j,{\rm{ }}k}})}^2} + K{{(T{\prime _{i,{\rm{ }}j,{\rm{ }}k}})}^2}]} $

(13)

其中, U′、V′和T′分别是无模式扰动试验及TEST2-SPPS试验的风场偏差和温度场偏差, $K = \frac{{{c_p}}}{{{T_r}}}$ , c_p为定压比热, T_r为参考温度。

${F_k} = \frac{1}{N}\sum\limits_{j = 0}^{N - 1} {{f_j}{e^{ - jk{\lambda _j}}}\left( {k = 0,1, \ldots ,N - 1} \right)} $

(14)

式中, N为纬圈格点总数, j=0, 1, …, N-1, 在这些格点上物理量的数值为f_j, k为纬向波数, F_k为谱分量, λ_j为各格点所在经度。

图 8为试验时段的12天平均总能量偏差波谱分析演变图, 从图中可以看出, 积分24~168 h, 不同尺度上的总能量偏差都随着积分时间增加而增长, 小尺度总能量偏差增加的速度小于大尺度总能量偏差。积分168~216 h后, 小尺度总能量偏差基本达到饱和, 大尺度总能量偏差仍随积分时间的增长而增加, 在积分216 h后达到饱和。由此说明随机物理扰动方案的扰动能量有随着积分时间的增加向大尺度传播的趋势。

5 小结和讨论

参考ECMWF的随机物理过程扰动方案, 设计了基于T213集合预报模式的随机物理扰动方案和随机总倾向扰动方案, 并对两种模式随机扰动方案进行了集合预报效果检验, 重点分析了随机物理扰动方案对预报变量的影响及扰动能量的传播机制。结果表明:

(1) 随机物理扰动方案概率预报性能较无模式扰动和随机总倾向扰动方案在不同程度上得到提高, 其中北半球热带外地区和热带地区的500 hPa高度和250 hPa风的概率预报改进最为明显, 东亚地区次之, 南半球基本没有改进。

(2) 随机物理扰动方案对降水预报也有较为明显的改进, 强降水中心值增强, 中雨以上量级集合预报降水评分提高, 降水概率预报技巧也得到了明显的改善。

(3) T213全球中期数值预报模式加入随机物理扰动方案和随机总倾向扰动方案后, 模式预报变量对其都有一定的敏感性。但随机物理扰动方案对预报变量的影响较随机总倾向扰动方案更加稳定, 随机物理扰动方案能更加合理地表现模式物理过程的不确定。随机物理扰动方案对预报变量影响的特征为:积分初期, 在垂直方向和水平方向上, 预报量对扰动敏感性较低, 随着积分时间的增加, 垂直方向和水平方向上的预报量的扰动逐渐增大, 南北半球中高纬地区的扰动增长大于赤道地区, 且南半球大于北半球。中低高层的风场、高度场和温度场的绝对离差大值区有随着积分时间的增加从低纬向中高纬传播的趋势, 比湿q因其本身的分布特征, 随积分时间的增长, 其扰动一直集中在中低纬地区。

(4) 对12天平均的总能量偏差进行波谱分析得到, 积分24~168 h, 不同尺度上的总能量偏差都随着积分时间增加而增长, 小尺度总能量偏差增加的速度小于大尺度总能量偏差。积分168~216 h后, 小尺度总能量偏差基本达到饱和, 大尺度总能量偏差仍随积分时间的增长而增加, 在积分216 h后达到饱和。由此说明随机物理扰动方案的扰动能量有随着积分时间的增加向大尺度传播的趋势。