暴雨是我国常见的局地和区域极端天气事件。局地暴雨与β中尺度的对流性系统相联系, 但β中尺度的对流性系统又是天气尺度系统的产物。天气尺度系统中往往包含先后发生的多个β中尺度的对流性系统, 于是形成了区域持续性的暴雨事件(丁一汇, 1994)。在常规的天气图上, 区域暴雨多位于低空急流的左侧和切变线的右侧, 但暴雨相对天气尺度(或次天气尺度)系统中心的距离不确定, 给暴雨发生的物理解释和落区预报增加了难度。
在日常的暴雨预报业务中, 预报员的信息来源主要是天气图和数值预报产品。天气图上和数值天气预报产品中的低层大气风场(流场)分析是暴雨诊断和预报的通常做法。在有利的大气水汽条件下, 气流辐合与暴雨落区应有直接的联系。但观测的气流中包含了不同的尺度, 人们试图从观测风场中分离掉那些与暴雨没有直接联系的部分, 而仅保留与暴雨有直接联系的扰动部分。水平风场作为一种矢量, 可以根据Helmholtz原理并利用流函数和势函数, 将风场分解为旋转风分量和辐散风分量(Hoskins et al, 1965)。风场的分解试图要有物理含义, 又要有应用价值。黄思训等(2007)把观测的台风流场分解成无旋流场、对称流场和不对称的涡旋对三个分量, 由此风场的分解可以认识台风的运动机理。为了分析暴雨中尺度系统的内部结构, 周玉淑等(2012)介绍了Chen等(1992a; 1992b)的调和正弦函数法和调和余弦函数法的分解原理, 认为调和余弦函数分解法的计算结果更为准确, 收敛也快。利用调和余弦函数分解法, 邓涤菲等(2012)对一次东北冷涡暴雨过程中的风场做了无旋转和无辐散分量的分解分析。这些都是区域风场的数学(函数)分解。在全球角度上, 刘海明等(2007)将全球大尺度的环流分解为Rossby波动的水平分支, 经向垂直剖面内的Hadley环流和纬向垂直剖面内的Walker环流, 用来描述全球大气的主要运动形态。这样的分解能够很好地描述大尺度三维空间环流的协同变化特征, 但对与天气尺度相联系的局地扰动环流难以反映。大气风场具有全球的和区域的或局地的多时空尺度特征, 同时它们的形成也是有物理含义的。既要从全球的角度, 又要体现区域差异, 并且具有物理含义地分解观测的风场才是有实用意义的。基于这一考虑, 我们从气象要素的多时空变化本质出发, 发展了一个新的大气变量物理分解的方法(钱维宏, 2011; 2012a)。它不但能够分解出行星尺度的气候环流和行星尺度的扰动环流, 还可提取出区域尺度的瞬变扰动风分量。在应用方面, 我们用美国再分析风资料做了瞬变扰动风与区域暴雨落区的关系分析(钱维宏等, 2012a)。最近, 我们又用更高分辨率的欧洲再分析资料做了瞬变扰动风的分析, 得到了比用美国再分析资料更有实用意义的结果。本文在介绍大气瞬变扰动风的提取方法之后给出欧洲高分辨率风场资料在中国东部区域暴雨分析中的应用。
1 资料和方法本文使用的基本资料是观测降水和大气风。降水资料来源于中国气象局国家气象信息中心的中国大陆754个观测站的数据, 日(24 h)降水量的统计时段为北京时间前日20时至当日20时。850 hPa风场来源于欧洲中期天气预报中心(ECMWF)ERA Interim的全球再分析资料, 空间分辨率是0.75°×0.75°经纬度格距, 时间分辨率是6 h, 包含世界时00:00、06:00、12:00和18:00时4个时次。用全球原始再分析风场减去相应时次的30年(1981—2010年)风场平均值, 再减去各个纬度的瞬时平均值, 得到瞬变扰动风场。
我们具体介绍大气风场分解的原理。传统意义上, 气候被定义为月、季或年时间平均的大气状态(Peixoto et al, 1992)。与此不同的是, 我们考虑地球上一个点的气候是在某个太阳高度角下太阳辐射与下垫面动力和热力平衡的大气随时间规则变化的状态。这个气候具有日循环的变化和年循环的变化, 但不包含多尺度天气扰动和多时空尺度气候扰动的部分。于是, 全球大气风场、位势高度场和温度场等气象要素都可以物理分解成4个分量:纬圈平均的对称气候、非对称气候、纬圈平均的瞬变对称扰动和瞬变非对称扰动(钱维宏, 2012b)。
以全球风场为例, 4分量分解可以写成:
| $\begin{array}{l} \mathit{\boldsymbol{V}}{\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)_{d,{\rm{ }}y}} = {\left[ {\mathit{\boldsymbol{\overline V}} \left( {\varphi ,{\rm{ }}t} \right)} \right]_d} + {\mathit{\boldsymbol{V}}^*}{\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)_d} + \\ \quad \quad \quad \quad \quad \quad \,\;\;\left[ {\mathit{\boldsymbol{V}}\left( {\varphi ,{\rm{ }}t} \right)} \right]{\prime _{d,{\rm{ }}y}} + \mathit{\boldsymbol{V}}\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)\prime _{d,{\rm{ }}y}^* \end{array}$ | (1) |
式中, 左端项V(λ, φ, t)d, y是历史或当前时刻t的观测风矢。这个风场是全球的, 是经度λ和纬度φ的函数。它的观测是在确定年份y中的某一日d的某一时刻t, 如世界时00:00时(北京时08:00时)。
式(1) 中右端第一项[V(φ, t)]d是纬圈平均的气候对称风。它反映的物理意义是不同地理纬度带上太阳高度角(辐射)变化引起的风场响应。它的变化位相大约滞后太阳季节高度角的变化40多天(Qian et al, 2010)。由历史(N)30年同一时刻t的纬圈P个格点观测风场, 我们可以通过下式计算得到
| ${\left[ {\mathit{\boldsymbol{\overline V}} \left( {\varphi ,{\rm{ }}t} \right)} \right]_d} = \sum\limits_{y = 1}^N {\sum\limits_{\lambda = 1}^P {\mathit{\boldsymbol{V}}{{\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)}_{d,{\rm{ }}y}}/\left( {N \times P} \right)} } $ | (2) |
它是年循环(365 d)中第d天第t时刻(一日24 h)的全球对称气候风场。
式(1) 中第二项V*(λ, φ, t)d是时间平均的非对称气候。它虽然没有长期的或年际的变化, 但它具有日循环t(一日24 h)的和年循环d(一年365 d)的变化。它由下式通过(N)30年同一时刻t的观测资料估算得到
| ${\mathit{\boldsymbol{V}}^*}{\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)_d} = \sum\limits_{y = 1}^N \mathit{\boldsymbol{V}} {\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)_{d,{\rm{ }}y}}/N - {\left[ {\mathit{\boldsymbol{\overline V}} \left( {\varphi ,{\rm{ }}t} \right)} \right]_d}$ | (3) |
在大尺度上, 它反映的是海陆热力对比随时间变化引起的风场日循环和年循环变化。在小尺度上, 它反映的是局地地形差异和城市等下垫面热力和动力作用引起的规则风场日循环和年循环变化。这部分气候分量可以反映全球季风环流、区域季风环流和局地环流的季节变化与日变化。
上述两个气候风场的叠加就是通常意义上的多年平均的气候风场
| $\begin{array}{l} \mathit{\boldsymbol{\widetilde V}}{\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)_d} = \sum\limits_{y = 1}^N \mathit{\boldsymbol{V}} {\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)_{d,{\rm{ }}y}}/N\\ \quad \quad \quad \quad \quad = {\left[ {\mathit{\boldsymbol{\overline V}} \left( {\varphi ,{\rm{ }}t} \right)} \right]_d} + {\mathit{\boldsymbol{V}}^*}{\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)_d} \end{array}$ | (4) |
但它也具有日循环和年循环的变化, 用多年(如N=30年)同一时刻t的观测资料就可以估算得到①。
① 应用美国NCEP/NCAR 30年(1981—2010年)每日4时次(世界时00:00, 06:00, 12:00, 18:00时)再分析资料和欧洲ERA-Interim 30年(1981—2010年)每日4时次(世界时00:00, 06:00, 12:00时)再分析资料, 北京大学钱维宏研究组按照式(2) 和式(3) 已经计算得到了两套日循环和年循环的气候场。
式(1) 右端第三分量是纬圈平均的瞬变对称扰动风
| $\left[ {\mathit{\boldsymbol{V}}\left( {\varphi ,{\rm{ }}t} \right)} \right]{\prime _{d,{\rm{ }}y}} = \sum\limits_{\lambda = 1}^N \mathit{\boldsymbol{V}} {\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)_{d,{\rm{ }}y}}/P - {\left[ {\mathit{\boldsymbol{\overline V}} \left( {\varphi ,{\rm{ }}t} \right)} \right]_d}$ | (5) |
它不但是纬度的函数, 也随每天不同的时刻、每年不同的日期而变。这个纬圈平均的瞬变对称扰动在中纬度地区反映西风指数循环的变化, 在高纬度地区反映南极涛动和北极涛动指数的变化(钱维宏等, 2012b)。我们称第三项为行星尺度的瞬变扰动风。
式(1) 右端第四分量是瞬变非对称扰动风V(λ, φ, t)′d, y, 它是每时每刻变化的。从观测的当前风场中分离掉气候风场和行星尺度的瞬变扰动风场, 得到下列形式的全球扰动风场, 即
| $\begin{array}{l} \mathit{\boldsymbol{V}}\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)\prime _{d,{\rm{ }}y}^* = \mathit{\boldsymbol{V}}{\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)_{d,{\rm{ }}y}} - \mathit{\boldsymbol{\widetilde V}}{\left( {\lambda ,{\rm{ }}\varphi ,{\rm{ }}t} \right)_d} - \\ \quad \quad \quad \quad \quad \quad \quad \left[ {\mathit{\boldsymbol{V}}\left( {\varphi ,{\rm{ }}t} \right)} \right]{\prime _{d,{\rm{ }}y}} \end{array}$ | (6) |
我们也可以把两个气候风场与行星尺度的瞬变扰动风场的合成称为一个时刻的环境风场(
1991年夏季, 江淮流域发生了持续性的暴雨, 导致了江淮地区的严重洪涝灾害(丁一汇, 1993)。这次暴雨过程主要是静止锋及其锋面波动(江淮气旋)两种环流系统下的降水。图 1是1991年6月29日至7月11日持续性暴雨过程中的7月1日08:00时(北京时)850 hPa原始流场和扰动流场与24小时站点累积降水量的分布。在欧洲高分辨率的850 hPa原始流场上, 江淮区域暴雨带位于低空急流的左侧和风场辐合线的右侧。但在850 hPa扰动流场图中, 江淮区域暴雨带位于扰动气流的辐合线上。扰动气流辐合线南侧的西南风扰动气流与北侧的东北风扰动气流势力相当, 呈对峙的辐合状态。在对峙的扰动气流辐合线作用下, 暴雨带相对稳定。比较图 1a与1b可见, 扰动气流辐合线对暴雨带的位置有很好的对应关系, 而原始流场中的辐合线和西南低空急流与暴雨带之间的距离难以定量确定。图 1中原始流场与扰动流场之间存在着差异, 如中印半岛上原始流场上有一槽, 但在扰动流场上为反气旋环流。图 1的原始流场和扰动流场中各有两条槽线(切变线), 并不是有槽线(切变线)就出现降水, 还需要水汽(湿度)条件。这两条北方的扰动槽线上并没有出现强降水。不同的是, 扰动流场东部的暖切变明显, 与扰动流场切变线对应有两个相邻的站出现了暴雨。
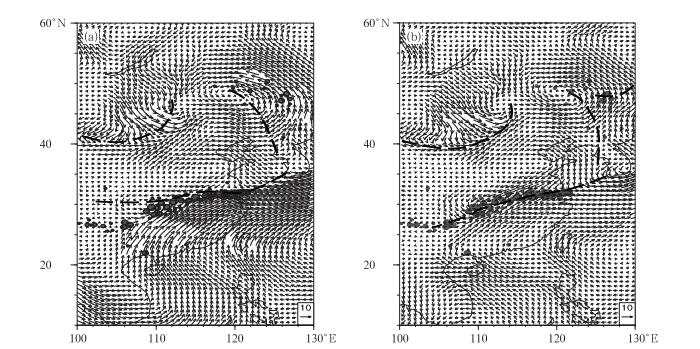
|
图 1 1991年7月1日江淮区域暴雨(圆点)与08:00(北京时)850 hPa原始气流(a)和扰动气流(b) (单位:m·s-1) [圆点由大至小分别为站点上的24 h(前日20:00时至当日20:00时)累积特大暴雨(R≥250 mm)、大暴雨(249.9 mm≥R≥100 mm)、暴雨(99.9 mm≥R≥50 mm)、大雨(49.9 mm≥R≥25 mm)和中雨(24.9 mm≥R≥10 mm), 粗虚线为气流辐合线、切变线或槽线] Fig. 1 The rainstorm in the Jianghuai region on 1 July 1991 and 850 hPa observed winds (a) and regional-scale wind anomalies (b) at 08:00 BT (unit: m·s-1) [The dots in descending size are corresponding to extreme rainstorm (R≥250 mm), heavy rainstorm (249.9 mm≥R≥100 mm), rainstorm (99.9 mm≥R≥50 mm), heavy rain (49.9 mm≥R≥25 mm) and moderate rain (24.9 mm≥R≥10 mm), respectively. The accumulated precipitation R is determined by the interval of 24 hours (from the former 20:00 BT to the current 20:00 BT the current day). Dashed lines indicate the lines of convergence, shear and trough] |
1991年7月3日暴雨带的重心位置相对7月1日东移。图 2给出的是7月3日暴雨带与850 hPa原始流场和扰动流场的分布。在850 hPa上, 7月1—3日长江上游地区存在一个气旋性的环流中心。7月3日, 暴雨带仍然位于850 hPa西南低空急流的左侧和切变线的右侧。但在850 hPa扰动流场中, 暴雨带位于扰动气流的辐合线上, 暴雨带两侧扰动气流呈对峙的辐合状态, 对应为稳定的强降水。
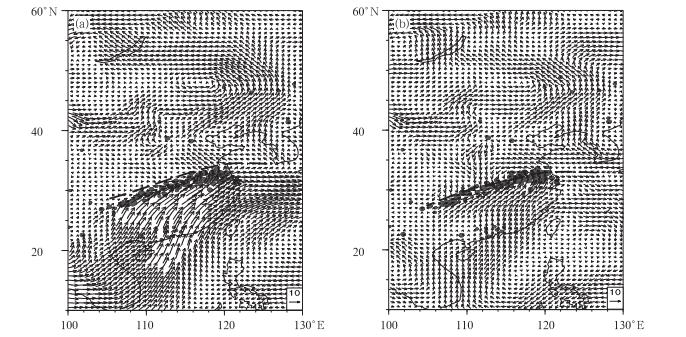
|
图 2 同图 1, 但为1991年7月3日江淮区域暴雨与08:00时850 hPa原始气流(a)和扰动气流(b)(单位:m·s-1) Fig. 2 As in Fig. 1, but on 3 July 1991 |
1991年7月5日, 江淮流域的暴雨分成了两个中心, 分别位于长江的中游和下游。850 hPa原始流场和扰动流场上, 与两个暴雨中心对应, 存在两股气流的辐合。在原始流场上, 暴雨中心仍然位于低空急流的左侧和切变线的右侧。但在850 hPa扰动气流中, 两个暴雨中心都位于扰动气流辐合线上。扰动气流的辐合与对峙及其存在的两个辐合中心, 对应着两个暴雨区。
3 黄河气旋和冷锋槽线区域暴雨分析造成我国区域性的暴雨, 除了南方气旋(位于梅雨锋上的江淮气旋和位于华南静止锋上的气旋)外, 在北方地区主要是黄河气旋和东北气旋。图 4给出了黄河气旋环流下的区域性暴雨。2004年7月11日, 850 hPa原始流场和扰动流场上的黄河气旋中心位于黄河下游。原始流场上, 气旋暖区中西南低空急流明显, 而气旋冷区中偏北气流较弱。850 hPa扰动流场上, 气旋冷式切变线两侧和暖式切变线两侧的扰动气流强度相当。对气旋性系统, 原始流场的气旋性中心及其切变线和扰动流场的气旋性中心及其切变线相对暴雨的位置基本相同。很多的例子分析得出, 在温带气旋和热带气旋的深厚环流系统中, 原始流场系统和扰动流场系统与暴雨落区的对应关系相当(钱维宏等, 2012; 2013)。
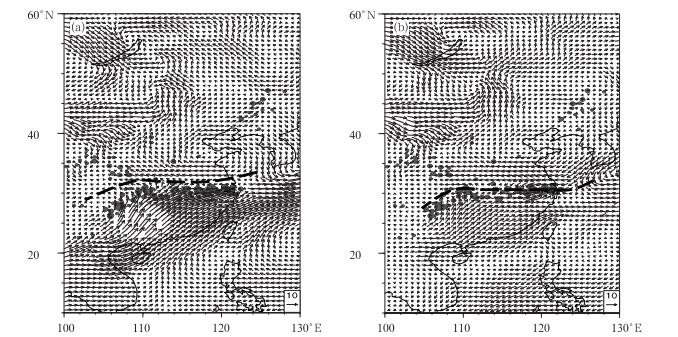
|
图 3 同图 1, 但为1991年7月5日江淮区域暴雨与08:00时850 hPa原始气流(a)和扰动气流(b)(单位:m·s-1) Fig. 3 As in Fig. 1, but on 5 July 1991 |
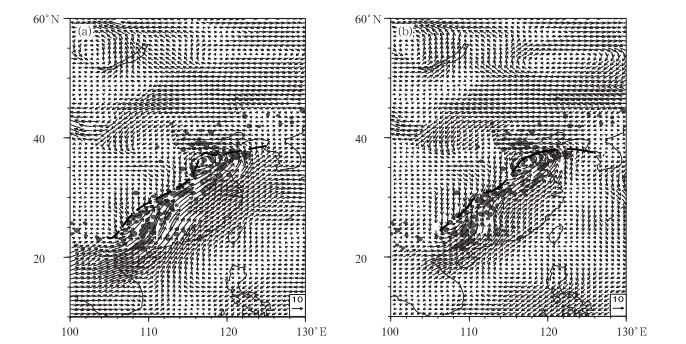
|
图 4 同图 1, 但为2004年7月11日黄河气旋区域暴雨与08:00时850 hPa原始气流(a)和扰动气流(b)(单位:m·s-1) Fig. 4 As in Fig. 1, but for a Yellow River cyclone rainstorm on 11 July 2004 |
北方降水系统的另一形式是冷锋槽线。2004年9月20日, 850 hPa原始流场上, 分别存在着东北气旋、江淮气旋和西南涡。江淮气旋西侧由北向南有明显的冷空气平流。江淮切变线附近存在冷锋。冷锋后或槽后的偏北气流中有两个暴雨区(图 5a)。在850 hPa扰动流场上, 槽后偏北扰动气流的方向和强度分股明显, 槽前扰动西南气流较强, 故扰动气流切变线弯曲明显(图 5b)。弯曲的扰动气流辐合线和偏北气流中的分股切变线更逼近两个暴雨中心。所以, 850 hPa上的扰动气流及其扰动辐合线与区域暴雨之间有较好的天气学对应关系。
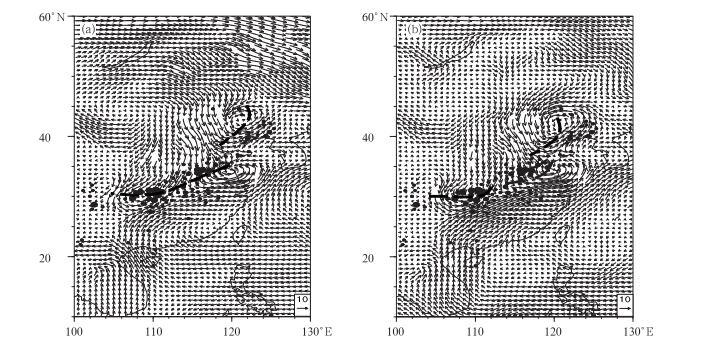
|
图 5 同图 1, 但为2004年9月20日冷锋槽线暴雨与08:00时850 hPa原始气流(a)和扰动气流(b)(单位:m·s-1) Fig. 5 As in Fig. 1, but for cold-front troughs rainstorm on 20 September 2004 |
本文介绍了大气流场物理分解的原理及其在区域暴雨分析中的应用。在850 hPa的原始流场中, 区域暴雨多位于低空急流的左侧和辐合线(切变线)的右侧。这种天气系统的描述难以确定暴雨的位置。与此不同, 暴雨带多位于850 hPa扰动气流的辐合线上。当850 hPa辐合线两侧的扰动气流呈对峙状态时, 暴雨带多为稳定。
本文给出的三次暴雨过程的例子已经用美国再分析风资料做过分析(钱维宏等, 2012a), 其中有4日暴雨也绘制在《中国区域暴雨扰动环流图集》中(钱维宏, 2013)。美国风场分解的扰动气流与区域暴雨的对应关系与上述欧洲再分析风场分解的扰动风与区域暴雨的对应关系一致。所不同的是, 欧洲再分析资料的空间分辨率高, 扰动风系统与区域暴雨的天气学关系更清楚。比如, 1991年7月的3 d欧洲再分析风分解的扰动气流辐合线和扰动气旋中心位置对应于区域暴雨的落区。又比如, 2004年9月20日, 欧洲再分析风分解的扰动气流槽线有弯曲或有分股气流, 与两个暴雨区的关系更紧密, 而美国再分析风分解的扰动气流槽线难以画出这样的弯曲或分股气流。
本文的结果指出, 利用高分辨率的欧洲再分析大气变量做极端天气事件的同期分析效果会比低分辨率的美国全球分析资料好。中期数值天气预报模式预报的风场可以应用于区域暴雨等极端天气事件的天气学和动力学释用。先前对2010年发生在中国夏季的暴雨事件做分析发现, 美国中期模式的环流预报结果分解的扰动风分量对区域暴雨的指示能力平均可提前3 d, 而欧洲中期模式的环流预报结果分解的扰动风分量对区域暴雨的指示能力平均可提前7 d左右(钱维宏等, 2012a)。因此, 在业务中期暴雨预报中可以用如上的方法分解欧洲中期天气预报模式的产品, 对未来1~10 d的区域暴雨做出预报。
邓涤菲, 周玉淑, 王东海, 2012. 有限区域分析方法在2006年一次东北冷涡暴雨分析中的应用[J]. 地球物理学报, 55(6): 1852-1866. DOI:10.6038/j.issn.0001-5733.2012.06.006 |
丁一汇, 1993. 1991年江淮流域持续性特大暴雨研究[M]. 北京: 气象出版社.
|
丁一汇, 1994. 暴雨和中尺度气象学问题[J]. 气象学报, 52(3): 274-283. DOI:10.11676/qxxb1994.036 |
黄思训, 蔡其发, 张铭, 等, 2007. 台风风场分解[J]. 物理学报, 56(5): 3022-3027. DOI:10.7498/aps.56.3022 |
刘海明, 胡淑娟, 徐明, 等, 2007. 全球大气环流三维分解[J]. 中国科学D辑, 12: 1679-1692. DOI:10.3321/j.issn:1006-9267.2007.12.014 |
钱维宏. 2011. 基于大气变量物理分解的低温雨雪冰冻天气的中期预报系统和方法. 中国, CN10222174A. 2011-10-19.
|
钱维宏, 2012a. 天气尺度瞬变扰动的物理分解原理[J]. 地球物理学报, 55(5): 1439-1448. |
钱维宏, 2012b. 中期-延伸期天气预报原理[M]. 北京: 科学出版社.
|
钱维宏, 2013. 中国区域暴雨扰动环流图集[M]. 北京: 气象出版社.
|
钱维宏, 单晓龙, 朱亚芬, 2012a. 天气尺度扰动流场对区域暴雨的指示能力[J]. 地球物理学报, 55(5): 1513-1522. |
钱维宏, 梁浩原, 2012b. 行星尺度纬圈平均风扰动的传播与南北极涛动[J]. 科学通报, 57(15): 1326-1333. |
钱维宏, 李进, 单晓龙. 2013. 中期模式扰动风在2010年区域暴雨预报中的天气学释用. 中国科学, 待刊. http://www.cnki.com.cn/Article/CJFDTotal-GZKX201605011.htm
|
周玉淑, 曹洁, 2012. 有限区域风场分解和重建[J]. 物理学报, 59(4): 2898-2906. |
Chen Q S, Kuo Y H, 1992a. A consistency condition for wind-field reconstruction in a limited area and a harmonic-cosine series expansion[J]. Monthly Weather Review, 120(11): 2653-2670. DOI:10.1175/1520-0493(1992)120<2653:ACCFWF>2.0.CO;2 |
Chen Q S, Kuo Y H, 1992b. A harmonic-sine series expansion and its application to reconstruction problems in a limited area[J]. Monthly Weather Review, 120(1): 91-112. DOI:10.1175/1520-0493(1992)120<0091:AHSSEA>2.0.CO;2 |
Hoskins H F, Rosenthal S L, 1965. On the computation of the stream functions from the wind field[J]. Monthly Weather Review, 93(4): 245-252. DOI:10.1175/1520-0493(1965)093<0245:OTCOSF>2.3.CO;2 |
Peixoto J P, Oort A H.1992.Physics of Climate. Springer. 520pp.
|
Qian W H, Tang S Q, 2010. Identifying global monsoon troughs and global atmospheric centers of action on a pentad scale[J]. Atmospheric and Oceanic Science Letters, 3(1): 1-6. DOI:10.1080/16742834.2010.11446841 |
 2013, Vol. 39
2013, Vol. 39 