人工神经网络(ANN)已经在过去的气象科研中得到了大量的研究(蔡煌东等,1994;孙照渤等,1998;金龙等,1999;2003),特别是基于误差反向传播算法的人工神经网络(简称BP-ANN),由于其成功地解决了求解非线性连续函数的多层前馈神经网络权重调整问题,得到较快发展,并且在一些业务部门得到推广(曾晓青,2010)。目前优化神经网络提高预测的方法主要有混沌理论(曹杰等,1997),PSO方法(傅强等,2004;李丙春等,2007)等,这类优化方法都是改变神经网络的求解方式,但运算加大,收敛速度慢,也很容易陷入局部解。另外通过融合另外一种方法进来提高预测准确率,比如小波(金龙等,2000)、模糊技术(韦一等,2007)。这类方法并未从神经网络自身方案改进。本次研究将从神经网络内部着手,进行网络改进。众所周知BP-ANN的学习训练过程由两部分组成,即输入因子正向传播和误差信息反向传播(简称BP), 在一个完整的3层结构的BP-ANN中,包括输入层、隐层和输出层, 在本文中称为单隐层神经网络。整个网络所要求解的是隐层以及输出层的权重值,那么在一个隐层神经元个数确定及神经元映射函数确定的情况下,在BP训练求解过程中需要输入的参数有:最大训练迭代次数、隐层学习率、输出层学习率和动量因子。对于BP-ANN训练有这样的一个问题,对于同一个样本模型、同样的网络结构和同样的输入参数情况下,每次训练得到的权重和最终的误差结果几乎都是不一样的,有的会很好,有的会较差。无论你怎么调节学习率和动量因子这些输入参数,其拟合准确率的提升空间也很小,对未来预测样本准确率的提升能力(后称泛化能力)就更小。另外,在业务的应用中,特别是在数值预报解释应用中,每个模型的输入因子都是不一样的,那么BP-ANN的隐层神经元结构应该是一个动态的神经元个数。再之,数值预报解释应用中的模型训练是大规模的(成千上万的),在利用BP-ANN建模训练中,希望都能寻找到每个模型的局部相对较优的解,具有较好的泛化能力。为了提高BP-ANN在业务预报中的建模和预测能力,本次将利用BP-ANN作为训练预报模型的建模工具,针对BP-ANN模型内部的权重的初始方式、初始权重次数和隐层神经元的个数等问题进行深入研究,并且通过数值模拟与实况对比,给出改进前后的BP-ANN模型预报效果对比情况,为以后BP-ANN的研究以及业务化应用提供一些有力的参考依据。
1 数据和评判标准气象站点的信息列在表 1中,本次研究收集了北京周边4个气象站2009—2011年的逐日最高温度观测资料。该数据作为模型文件中的目标拟合和检验数据。
|
|
表 1 气象站点信息 Table 1 The information of meteorological stations |
模型文件中的因子数据来自中国气象局下发的T639数值预报模式的输出产品。所收集的资料从2009年1月1日至2011年12月31日逐日预报场资料, 包括温度、高度、纬向风、经向风、垂直速度、比湿、相对湿度、风速、海平面气压、地面温度、地面气压、10 m纬向风、10 m经向风、2 m温度、2 m相对湿度等。模型中因子通过相关系数和逐步回归控制后得到的24小时预测因子模型文件,具体可参考文献(曾晓青等,2009)。由于本文重点讨论BP-ANN的模型问题,所以对于因子模型的生成,这里不再详细讨论。模型中的建模样本为2009—2010年每年的5月15日至9月15日,总共约240天的训练样本数据,另外验证样本选择2011年5月15日至9月15日的数据,总共约115天的验证样本数据。这里需要强调的是站点的选择和样本时间等的选择不会影响试验的结果,因为在因子模型固定的情况下,改进前后的BP-ANN训练都是在针对同一个因子模型的基础上进行,所以就与前面整个因子模型如何得到的是没有太多直接关系。但是对于不同季节、不同站点和不同预测时效的因子模型,改进后的建模方法相对于改进前的预测命中率提高程度是不一定的。所以本文的重点在纵向对比而非横向比较。
大多数BP-ANN训练中的评判标准为平均绝对误差,然而,这个标准有一定的缺陷,原因在于你不容易知道:是由于对一个样本的拟合误差大幅减小带来的误差减小,还是由于对大多数样本拟合误差、微小误差同时减小而累积的误差减小,如果网络让某些样本误差很小而另外一些样本误差较大这样很容易让网络陷入局部解。我们的目的是希望让每个样本误差都减小到允许误差之内,而不是某个样本误差很小,而某个样本误差很大,所以我们选择的评判标准为命中率。命中率是从总体上来描述正确的预报样本所占总预报样本的百分比。因为拟合对象为最高温度, 所以容忍误差为2℃,其公式:
| $命中率 = \frac{{\left( {\left| 误差 \right| \le 2℃} \right)的样本数}}{\quad \quad \quad \quad 总样本数\quad \quad \quad \quad \quad }$ | (1) |
准确率的范围:0~1,0为最差得分,1为最好得分。
2 模型理论与数值试验本文所采用的ANN结构是常用的BP单隐层网络结构,隐层神经元采用Sigmoid函数,输出层神经元为线性函数,对隐层和输出层使用不同的学习效率,以提高收敛速度。这里将不再详述BP-ANN的整个求解推导过程(曾晓青,2010)。网络中的学习率是梯度下降法中的步长调节参数,其目的是让网络大步搜索还是小步前进,动量因子是噪声样本的调节系数,通过原理可以看出,无论怎样调节这几个参数都很难大幅提高网络的预测能力和网络稳定性。我们根据使用经验,在本次试验中对这几个参数采用固定形式,即第一层学习率为0.75,第二层学习率为0.06,动量因子取0.70。任何一个统计模型最重要的目标是训练后的模型具有较高的泛化能力,虽然通过交叉验证中的留一法手段可以进行一定的推测,但是也并不是实际的未来预测能力。另外在求解过程中速度问题使得留一法受到很大限制。所以对BP-ANN训练误差的改进目标是让整个网络对整体训练样本的拟合命中率达到一个较高的值(非平均绝对误差)。下面介绍3种方法对BP-ANN建模训练的改进试验,然后将每种改进后的试验结果与改进前的进行比较,得出结论,最后集成3种改进的方法于一个BP-ANN中和未改进的BP-ANN进行对比,得出最终结果。下面我们就进行这些数值试验来说明。
2.1 权重初始方式对神经网络求解的敏感性试验在求解BP-ANN的开始,需要给BP-ANN的隐层以及输出层权重一个随机的初始场,然后通过不断的迭代,修改每个神经元的权重大小,使得最终的输出结果与实际观测值的差值达到一个可以容忍的范围。可以看出,最终的网络输出结果是由最初给定的一个随机权重初始场不断更新后,得到一个优化的权重场,根据这个优化的权重场而得到最终的拟合值。那么初始的权重场就对后面的拟合数据会起到一定的决定作用。那么初始权重场该取一个什么样的随机数比较合适呢?这里通过给初始权重两种不同的随机分布场,来比较其两种随机分布产生的初始权重场对结果会有怎么样不同的影响。第一种随机分布是常用于BP-ANN中产生初始权重的均匀分布,第二种分布是高斯分布,研究中产生高斯分布的随机数使用Box Muller方案。Box Muller方法是通过均匀分布的随机数来产生一个高斯分布的随机数,公式为:
| $z = \mu + \sigma \cos \left( {2{\rm{ \mathsf{ π} }}t} \right)\sqrt { - 2\log \left( s \right)} $ | (2) |
式中,μ为均值,σ2为方差,s∈[0, 1],t∈[0, 1],s和t都是服从均匀分布的随机数。所得到的随机数z~N(μ, σ2)。
本次试验中4个模型因子数范围为8~11个,样本其余信息介绍在第一节。BP-ANN的隐层神经元个数根据Kolmogorov定理确定,其中常数取6(本次试验中隐层神经元个数固定),第一层学习率为0.75,第二层学习率为0.06,动量因子取0.70,训练次数为1000次。为了验证权重初始方式是否具有普遍性,整个训练过程重复进行20次(为了验证是否是随机性的)。
试验样本拟合结果如图 1,每一根实线表示以高斯分布产生初始权重的BP-ANN一次训练迭代过程中的命中率变化,每一根虚线以均匀分布产生初始权重的BP-ANN一次训练迭代过程中的命中率变化,重复了20次试验,各有20根线。结果表明随着训练迭代次数的增加,利用高斯分布产生的初始权重得到的拟合值与真实值之间的命中率比利用均匀分布所得到的命中率更容易向1值靠近。特别是在迭代后期大部分利用均匀分布所得到的命中率增大得很慢甚至有的不再增加。而采用高斯分布产生的权重却可以随着迭代次数的增加而增加且可能性较高,说明整体误差在不断减小,这是我们希望看到的。可以得出,在BP-ANN求解过程中,初始随机权重场如果服从高斯分布将比服从均匀分布的BP-ANN有更高的整体样本的拟合命中率。
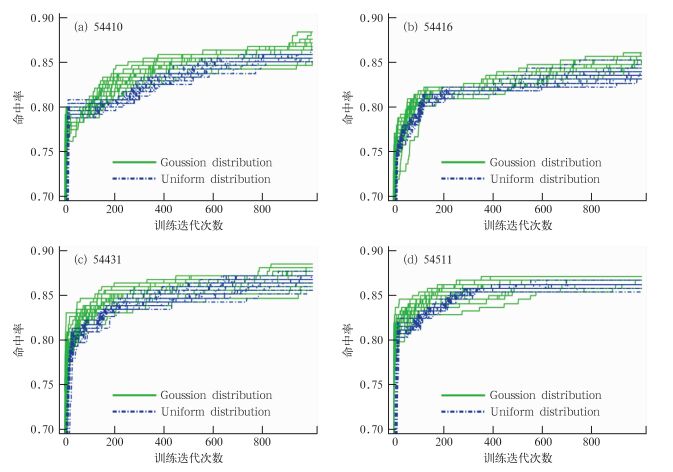
|
图 1 不同权重初始方式对拟合结果的命中率影响图 Fig. 1 Hit rate from fitting the data is influenced by different weights methods |
BP-ANN隐层权重采用高斯分布进行初始化虽然对BP-ANN的解起到优化作用,但是如果一开始初始化的权重就在一个局部最小值的周围,那么整个网络就很容易陷入这个局部最小值而很难跳出来,寻找到更优的局部解。以前的很多文献都提出通过修改学习率或者动量因子来避免陷入局部最小的危险,但是这不是容易的事,因为不会知道网络何时陷入了局部最小,学习率何时变大何时减小。所以这里提出通过多次初始化权重来加大整个解空间的搜索范围,使得BP-ANN能够以更大的几率靠近最优解。
本次试验中4个模型因子数范围为8~11个,样本其余信息介绍在第一节。BP-ANN的隐层神经元个数根据Kolmogorov定理确定,其中常数取6,第一层学习率为0.75,第二层学习率为0.06,动量因子取0.70,训练次数为1000次,权重初始场服从高斯分布。另外,初始权重初始化次数为5次,和同样条件下初始权重进行1次初始化的结果相对比。同样为了验证权重初始方式是否具有普遍性,整个训练过程重复进行20次(为了验证是否是随机性的)。
图 2中的方形虚线为经过5次初始化的BP-ANN训练的样本拟合命中率,实线为经过1次初始化的BP-ANN训练的样本拟合命中率,可以看出总体上经过5次初始化后BP-ANN求解得到的样本拟合命中率总是比1次初始化后BP-ANN求解得到的样本拟合命中率更高,而且重复了20次试验,基本都满足这一结论,说明整体误差在不断减小,这也是我们希望看到的。可以得出,经过多次初始权重初始化的BP-ANN比1次初始权重初始化的BP-ANN有更高的整体样本的拟合命中率。
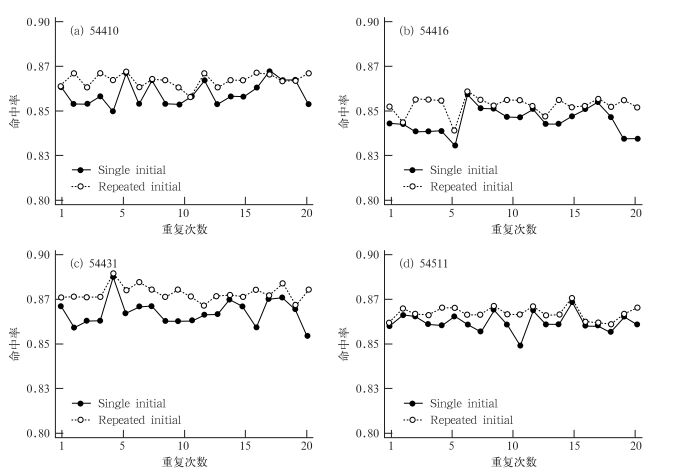
|
图 2 初始化次数对拟合结果的命中率影响图 Fig. 2 Hit rate from fitting the data is influenced by frequency of weights initialization |
BP-ANN的隐层神经元个数是重要的结构参数。隐层的神经元个数并不是越多越好,隐层的神经元过多会大大的加大训练时间,同时隐层的神经元个数的增加会造成网络的容错能力下降,因此隐层神经元的个数必须要适当的选取,不能太多,也不能太少,但由于每个因子模型中的因子数不同,所以每个网络建模模型的隐层神经元个数也应该不同。在数值预报解释应用中的建模模型多达上万个,不可能通过人工逐一测试,那么就需要根据输入因子进行一个动态的隐层神经元个数的选择。所以我们首先根据Kolmogorov(Jondarr, 1996; Mirchandani et al, 1989)定理确定最初的BP-ANN隐层神经元个数,并在其基础上对BP-ANN进行动态隐层神经元个数的选择。Kolmogorov定理可以表述为:
| $HN = \sqrt {n + m} + a$ | (3) |
式中,HN是隐层神经元个数,n是输入因子数,m是输出层神经元个数(这里为1),a是自然常数∈[1, 10]。以前BP-ANN中的a一般都取值为常数,而这里通过循环a值,不断地试算网络,比对不同隐层神经元个数的网络的拟合命中率,最后选取其中相对最优的拟合命中率的网络。
本次试验中4个模型因子数范围为8~11个,样本其余信息介绍在第一节。BP-ANN的第一层学习率为0.75,第二层学习率为0.06,动量因子取0.70,训练次数为1000次,权重初始场服从高斯分布。另外,隐层神经元个数根据Kolmogorov定理确定,其中固定隐层的常数a取为5,动态隐层的常数a从1~10循环。然后比较固定神经元个数的BP-ANN与动态神经元个数的BP-ANN对拟合结果命中率进行比较。同样为了验证权重初始方式是否具有普遍性,整个训练过程重复进行20次(为了验证是否是随机性的)。
图 3中的虚线为经过动态隐层神经元的BP-ANN训练的样本拟合命中率,实线为静态隐层神经元的BP-ANN训练的样本拟合命中率,可以看出总体上经过动态隐层神经元的BP-ANN求解得到的样本拟合命中率大部分比静态隐层神经元的BP-ANN求解得到的样本拟合命中率更高,而且重复了20次试验,基本都满足这一结论,其中有的比静态隐层神经元的BP-ANN求解得到的样本拟合命中率低是因为由于不同的初始场造成的(参看2.2节)。可以得出,经过动态隐层神经元的BP-ANN训练的样本比静态隐层神经元的BP-ANN训练的样本整体上有更高的整体样本的拟合命中率。
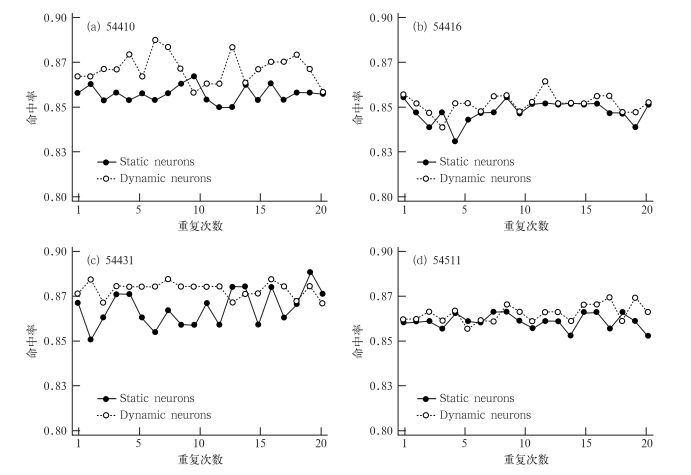
|
图 3 隐层神经元个数对拟合结果的命中率影响图 Fig. 3 Hit rate from fitting the data is influenced by hidden layer neurons |
上面进行的数值试验都是对已知样本的拟合后看其拟合命中率,虽然有的提高很少,有的提高很多,但是都仅限于对过去数据的拟合而不是预报,上面曾说过对于一个统计模型来说,模型对未来样本的预测能力是决定该模型好坏的重要标志。同样对于BP-ANN来说,其建立模型的泛化能力决定了它作为一个预测工具的成败,下面我们将通过集成上面3个改进的网络方法于一个BP-ANN中(即优化的BP-ANN),然后跟未集成的原始的BP-ANN方法(非优化的BP-ANN)进行对未来样本的预报对比数值试验。
本次试验选择2009—2010年每年5月15日至9月15日(约240天)的资料作为训练样本数据,选择2011年5月15日至9月15日(约115天)的资料作为验证样本数据。优化后的BP-ANN保存的最优权重是通过动态的改变隐层神经元个数(隐层神经元公式中的常数a从1~10循环),初始权重的5次初始化以及让初始权重采用高斯分布而得到的。未优化的BP-ANN的最优权重是通过确定静态的隐层神经元公式中的常数a(选择5),进行1次权重初始化以及让初始权重采用均匀分布而得到的。两个网络的第一层学习率为0.75,第二层学习率为0.06,动量因子取0.70,训练迭代次数为1000次。
图 4中三角虚线代表的是非优化的BP-ANN做出的预测结果与实况观测的命中率曲线,菱形实线代表的是优化的BP-ANN做出的预测结果与实况观测的命中率曲线。从图 4中可以看到优化后的BP-ANN得到验证样本的预测命中率都要高于未优化的BP-ANN得到的验证样本的预测命中率。由于使用命中率作为检验标准,说明优化后的BP-ANN具有更好的泛化能力。当然这里也必须指出,并不是利用优化后的BP-ANN就一定比优化前的BP-ANN训练出来的模型具有较好的预测能力,而是说优化后的BP-ANN比起优化前的BP-ANN在很大程度上加大了得到稳定的、泛化能力较好的模型的概率,并且训练出来的预测模型能从整体上提高未来样本预测准确率。
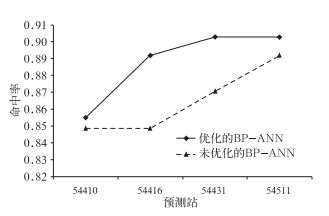
|
图 4 优化的BP-ANN与未优化BP-ANN对验证样本的预测命中率比较 Fig. 4 Hit rates compared between optimized BP-ANN and non-optimized BP-ANN |
BP-ANN在气象领域发挥了很多重要的统计建模的作用,特别是近些年来在数值预报解释应用中的应用逐渐增多,对BP-ANN的求解预测能力提出了更高的要求。为了让BP-ANN在模型求解中获得稳定并且泛化能力较强的预测模型数据,另外由于数值预报释用的客观要素预报水平要求不断提高,本文利用国家气象中心的业务预报模式T639模式的预报场资料作为释用的因子资料,以地面观测的最高温度资料作为释用的目标资料,选择北京地区4个气象站点的24小时预测因子模型作为研究对象。4个模型的因子模型文件通过逐步回归得到(本文非重点论述),因子模型样本为2009—2010年每年的5月15日至9月15日,总共约240天的训练样本数据。通过对4个模型样本的拟合建模试验发现:BP-ANN的随机权重初始场的权重值服从高斯分布(这里采用Box Muller方案),或者初始权重进行多次初始化,或者采用动态的隐层神经元网络结构这三个改进方法都能让BP-ANN对样本的拟合命中率有一定的提高。
为了衡量改进前后的BP-ANN方法建立出来的模型对未来样本的预测能力,通过集成3种改进方法于一个BP-ANN中,和未改进前的BP-ANN进行比较。验证样本选择2011年5月15日至9月15日的数据。总共约115天。对比后发现优化后的BP-ANN得到验证样本的预测命中率都要高于未优化的BP-ANN得到的验证样本的预测命中率。优化后的BP-ANN具有更好的泛化能力。
这里还应该强调的是,并不是说利用优化后的BP-ANN就一定比优化前的BP-ANN训练出来的模型具有较好的预测能力,而是说优化后的BP-ANN比起优化前的BP-ANN在很大程度上加大了得到稳定的、泛化能力较好的模型的概率,并且训练出来的预测模型能从整体上提高未来样本预测准确率。以上的方案都是通过增加寻找最优解的概率来获得较优的概率模型,那么势必会增加计算量。但是在预报之前,BP-ANN模型可以有足够的时间来进行建模,所以计算量虽然在某些程度上增加,因此不会困扰我们业务上的预报过程。
蔡煌东, 宫家文, 甘骏人, 等, 1994. 运用人工神经网络作汛期降水预报[J]. 气象科学, 14(4): 386-389. |
曹杰, 谢应齐, 1997. 一种基于混沌理论的联想记忆神经网络模型[J]. 热带气象学报, 13(1): 82-87. |
陈宁, 金龙, 袁成松, 1999. 最优子集的神经网络预报建模研究[J]. 气象, 25(1): 14-19. DOI:10.7519/j.issn.1000-0526.1999.01.003 |
傅强, 胡上序, 赵胜颖, 2004. 基于PSO算法的神经网络集成构造方法[J]. 浙江大学学报, 38(12): 1596-1600. DOI:10.3785/j.issn.1008-973X.2004.12.013 |
胡江林, 涂松柏, 冯光柳, 2003. 基于人工神经网络的暴雨预报方法探讨[J]. 热带气象学报, 19(4): 422-428. |
金龙, 陈宁, 林振山, 1999. 基于人工神经网络的集成预报方法研究和比较[J]. 气象学报, 57(2): 198-207. DOI:10.11676/qxxb1999.018 |
金龙, 罗莹, 王业宏, 等, 2003. 月降水量的神经网络混合预报模型研究[J]. 高原气象, 22(6): 618-623. |
金龙, 秦伟良, 姚华栋, 2000. 多步预测的小波神经网络预报模型[J]. 大气科学, 24(1): 79-86. |
李丙春, 孙蕾, 2007. 基于粒子群优化的神经网络预测模型[J]. 新疆大学学报(自然科学版), 24(4): 481-485. |
钱莉, 兰晓波, 杨永龙, 2010. 最优子集神经网络在武威气温客观预报中的应用[J]. 气象, 36(5): 102-107. DOI:10.7519/j.issn.1000-0526.2010.05.015 |
孙军波, 钱燕珍, 陈佩燕, 等, 2010. 登陆台风站点大风预报的人工神经网络方法[J]. 气象, 36(9): 81-86. DOI:10.7519/j.issn.1000-0526.2010.09.013 |
孙照渤, 谭桂容, 赵振国, 1998. 人工神经网络方法在夏季降水预报中的应用[J]. 南京气象学院学报, 21(1): 47-51. |
韦一, 佘勇, 王贤勤, 2007. 基于模糊Hopfield神经网络的大气降水粒子分类[J]. 成都信息工程学院学报, 22(5): 569-572. |
曾晓青. 2010. 模式输出统计技术在局地中短期天气预报中的研究与应用. 兰州大学博士学位论文.
|
曾晓青, 王式功, 刘还珠, 等, 2009. 统计降尺度方法在青海省冬季最低温度预报中的应用[J]. 高原气象, 28(6): 1471-1477. |
Jondarr C G H.1996.Back propagation family album.Technical Report C/TR96-05, Department of Computing, Macquarie University.
|
Mirchandani Gagan, Gao Wei, 1989. On hidden nodes for neural nets[J]. IEEE Transactions on Circuits and Systems, 36(5): 661-664. DOI:10.1109/31.31313 |
 2013, Vol. 39
2013, Vol. 39 