引言

降水预报在及时、准确的洪水预警和防灾减灾中扮演着极其重要的角色，水文预报从降水分布的预报到径流、洪峰的预报要经历多个步骤，其中每个步骤都可能存在不确定性。水文预报的用户越来越希望对水文预报的不确定性进行定量估计。因此，降水预报的不确定性对于水文预报不确定性有非常重要的影响。

降水预报是天气预报中具有挑战性的一项任务。随着数值预报技术的发展，降水预报的准确率得到了一定程度的提高。由于大气系统的复杂性和非线性加上模式初值误差和模式本身无法避免的一些不确定性，使得数值预报仍存在一定的误差(杜钧等，2010)。有技巧的降水数值预报是产生有技巧的水文预报的基础，将有一定技巧的单值降水预报生成包含不同可能性的概率预报产品，同时降低其预报偏差，产生使降水预报更加有技巧的产品，对于在防汛抗旱和水资源管理决策中服务不同需求的用户是非常有意义的。

集成预报技术主要是用于处理模式的随机误差，统计方法则可以用来消除系统性的误差，如MOS和PP就是这样的方法(Marzban et al, 2006)。但这些方法无法表达预报的不确定性。Hamill等(2006;2008) 提出使用Logistic回归方程来对降水数值预报进行订正。此外，国外学者通过二元随机变量的联合分布来实现对单个预报的概率化，这样做的好处是在概率化的过程中，考虑了历史资料的应用，不但实现了对数值预报进行订正，而且还将数值预报的不确定性进行了量化，使预报包含的不确定性信息更加完整。例如Krzysztofowicz等(1999)使用贝叶斯理论对数值预报进行了订正，还定量给出了数值预报的不确定性。Schaake等(2007)运用二元联合分布法将单值降水数值预报转化成了一系列有意义的降水概率预报，并在这些概率预报的基础上生成了集合预报，为水文集合预报提供了具有概率意义的降水预报。Wu等(2011)对二元联合分布进行了一定的改进，对改进效果的检验则再一次证明该方法能得到一个更有技巧的降水集合预报。

在气象-水文预报中常常要用到基于单个数值预报计算的面雨量^①预报，虽然可以较为容易地得到一个确定性预报，但是如何把预报的不确定性定量、完整地表达出来，在产品概率化的同时把历史资料的信息吸收进去，使得对预报不确定性的表达不但定量化，而且还具有一定的完整性，这方面的工作还需要一定的探索和尝试。因此，本文利用单值降水数值预报和对应的降水观测资料，在淮河流域的4个子流域上，建立了基于预报和观测的二元条件亚正态分布函数的概率预报模型。不但提高了预报技巧，而且实现了由确定性预报向概率预报的转化，并将预报的不确定性进行了定量表述，最后对应用效果进行检验和讨论。

^①面雨量是指某一时段内一定面积上的平均雨量。

1 研究流域概况和资料

淮河流域地处我国东部，位于30°55′~36°36′N、111°55′~121°25′E，介于长江、黄河之间，为东亚季风区，是我国南北气候的过渡地带，旱涝灾害频繁。该流域天气气候变化复杂，兼具南北特点，雨量相对丰沛但分布不均，是我国干旱、洪涝灾害最频繁的地区之一。本文参照中国气象局流域面雨量业务预报的流域划分^①，选择了淮河流域4个面积大小不同的子流域作为研究区域，按照流域面积从小到大的顺序排列分别是：枣庄到徐州(简记为A)，流域面积9.2×10³ km²；淮河上游大坡岭至息县流域(简记为B)，流域面积16.5×10³ km²；洪泽湖以下流域(简记为C)，流域面积30.6×10³ km²；蚌埠至洪泽湖流域(简记为D)，流域面积42.3×10³ km²(见图 1)。

^①《全国七大江河流域面雨量监测和预报业务规定(试行)》，中国气象局，2010年。

采用对应子流域内59个气象站点的24 h降水量(由前一日20：00至当日20：00，北京时，下同)为降水观测资料，总的时间序列长度为1981年1月1日至2003年12月31日，共计23年。降水数值预报资料取自美国国家大气管理局地球系统实验室(the Earth System Research Laboratory，ESRL)，来自NOAA的NCEP全球预报系统GFS的回算资料(reforecast)^②。该回算系统是由15个集合成员组成的集合预报系统，资料从1979开始回算至今，每12 h输出一次，模式水平分辨率为2.5°×2.5°。本文具体使用该回算资料的24 h降水量集合平均作为单值的确定性预报，为了叙述简便，以下简称这种资料为GFS单值预报。

^②http://www.esrl.noaa.gov/psd/forecasts/reforecast/details.html.

2 方法简介 2.1 流域面雨量的计算方法

对于流域的实际面雨量，本文采用较为常用的泰森多边形法进行计算(毕宝贵等，2003)。

为了简单起见，对应子流域的预报面雨量，则是采用距离子流域的几何中心位置最近的模式格点降水预报，作为该子流域面雨量预报近似值(图 1a)。实际面雨量的分月演变见图 1b，雨量主要集中在夏季(6—8月)。

2.2 单值预报生成概率预报的方法

正如引言所述，由于预报是有不确定性的，因此预报会出现一定的误差。一个单值预报在预报某一事件时，对应观测到的实况可能会是一系列的数值。例如预报25 mm降水，实况可能会出现25 mm，也可能是15 mm，也有可能是30 mm，或其他值。这些值会是[0，∞]上的任何数值，于是预报和实况出现了误差。为了计算在预报某事件发生的情况下，实际观测出现各种情况的概率，把预报的这种不确定性进行量化。利用单值预报的历史资料与观测资料建立一个单值预报和观测的二元联合分布函数，从而得到一个在某单值预报条件(例如条件为预报有25 mm降水)下的，实际观测出现各种情况的(条件)分布函数。进而得到在预报某事件发生的情况下，实际观测出现各种情况的可能性，即实际观测出现各种情况的概率。

具体的做法是采用Schaake等(2007)所用到的方法。用二元联合分布函数H(x, y)表示单值降水预报x和相应的降水观测y的关系。为得到在某单值预报的预报面雨量x的条件下，实际面雨量y出现的条件分布函数H_Y|X(y|x)，需要计算单值预报的降水预报x和降水观测y的边际气候累积分布函数(Climatological Marginal Distributions)，分别记为F(x)和G(y)。

由于x和y都是离散-连续型的随机变量，单值预报的降水预报的边际气候累积分布F(x)定义为：

$F\left( x \right) = 1 - {P_x},x = 0$

(1)

$F\left( x \right) = \left( {1 - {P_x}} \right) + {P_x}F\left( {X\left| {x > 0} \right.} \right),x > 0$

(2)

式中P_x为单值预报的降水发生概率；F(X|x>0) 为单值预报有降水发生时的降水概率分布。观测降水的边际气候累积分布函数G(y)与F(x)形式相同，F(x)与G(y)可为任意的函数，但必须是严格递增的连续函数。梁莉等(2011)用Gamma分布对淮河流域的降水分布拟合取得了很好的结果，因此本文也采用Gamma分布对F(X|x>0) 与G(Y|y>0) 进行估计。

在二元联合分布建立之前，首先将降水量进行正态化的处理。本文使用Kelly等(1997)描述的正态分位数变换(Normal Quantile Transform，NQT)来对降水量进行正态化。经过NQT变换后，假设(Z，W)的联合分布为二元标准正态分布，二元联合分布(X, Y|X＜x, Y＜y)被称为二元亚正态分布(Meta-Gaussian Bivariate Distribution)，其分布函数形式如下：

$\begin{array}{l} H\left( {x,y} \right) = P\left( {X,Y\left| {X ＜ x,Y ＜ y} \right.} \right) = \\ \quad \quad \quad \quad B\left\{ {{N^{ - 1}}\left[ {F\left( x \right)} \right],{N^{ - 1}}\left[ {G\left( y \right)} \right];\gamma } \right\} \end{array}$

(3)

式中，用B表示二元标准正态分布函数：B(z, w; γ)=P(Z≤z, W≤w|γ)，其中γ=Cor(Z, W)，是皮尔森相关系数。

在给定确定性预报X=x条件下，利用条件分布函数H_Y|X(y|x)估计观测Y的累积分布情况。由于x=0进行正态分位数变换后的值无法确定，估计条件分布时有以下两种情况：

第一种情况：当x>0时，进行分位数变换后值为z，由于(Z，W)的联合分布为二元标准正态，则条件亚正态分布为：

$\begin{array}{l} {H_{Y\left| X \right.}}\left( {y\left| {x > 0} \right.} \right) = {B_{W\left| Z \right.}}\left( {w\left| {z > {z_0}} \right.} \right) = \\ \quad \quad N\left\{ {\frac{{{N^{ - 1}}\left[ {G\left( y \right)} \right] - \gamma {N^{ - 1}}\left[ {F\left( x \right)} \right]}}{{\sqrt {1 - {\gamma ^2}} }}} \right\} \end{array}$

(4)

其中，条件平均为E(W|z)=γz；条件方差为Var(W|z)=1-γ²。得出在Z=z的条件下，W在给定p时的分位数：

${w_p}\left( z \right) = \gamma z + \sqrt {1 - {\gamma ^2}} {N^{ - 1}}\left( p \right)$

(5)

将得到的w_p(z)变换到原x，y的空间：

$\begin{array}{l} {y_{\left. p \right|x}} = {G^{ - 1}}\left\{ {N\left[ {B_{W\left| Z \right.}^{ - 1}\left( {w\left| {z > {z_0}} \right.} \right)} \right]} \right\} = \\ \quad \quad {G^{ - 1}}\left\{ {N\left[ {\gamma {N^{ - 1}}F\left( x \right) + \sqrt {1 - {\gamma ^2}} {N^{ - 1}}\left( p \right)} \right]} \right\} \end{array}$

(6)

第二种情况：当x=0时，变换后z≤z₀，z₀=N^-1(1-p_x)，但无法确定具体值，因此条件分布为：

$\begin{align} &{{H}_{Y\left| X \right.}}\left( y\left| x=0 \right. \right)={{B}_{W\left| Z \right.}}\left( w\left| z\le {{z}_{0}} \right. \right)= \\ &\quad \quad \int\limits_{-\infty }^{w}{\int\limits_{\infty }^{{{z}_{0}}}{b\left( z,w \right)}}\text{d}z\text{d}w/\int\limits_{-\infty }^{+\infty }{\int\limits_{-\infty }^{{{z}_{0}}}{b\left( z,w \right)\text{d}z\text{d}w}} \\ \end{align}$

(7)

相应的y_p|x为：

${y_{\left. p \right|x}} = {G^{ - 1}}\left\{ {N\left[ {B_{W\left| Z \right.}^{ - 1}\left( {w\left| {z \le {z_0}} \right.} \right)} \right]} \right\}$

(8)

其中p值即为H_Y|X(y|x=0) 的值。

式(6) 和(8) 确定后，可通过确定累积概率p，得到降水预报值为x条件下，累积概率为p的降水观测阈值y_p|x。在概率区间[0，1]上，给定等距离的n个概率{p=p₁, …, p_n}，则可以得到对应的一组降水预报值{y_p1|x, …, y_pn|x}的集合，在这样一组集合预报值的基础上就可以进行集合或者集成。

例如当单值预报降水量为1.2 mm，即x=1.2时，在概率区间[0，1]上，给定等距离的4个累积概率，即{p=p₁, …, p₄}分别为{0.25，0.5，0.75，1.0}，则每个降水值发生的概率为25%；然后通过式(6) 就可以得到对应的降水预报值，即{y_p1|x, …, y_p4|x}为{0.0，0.0，2.0，3.0 mm}，这些降水值的发生概率是相等的。这样就把一个预报量为1.2 mm的单值预报，转化成与上述4个累积概率区间相应的4个预报值，形成一组概率预报，即降水量预报值分别为0.0、0.0、2.0和3.0 mm，而且它们出现的概率均为25%。

2.3 概率预报的检验方法

通过式(6) 和(8) 得到的多个预报(集成预报)的集成平均预报与GFS模式集合平均预报(可以看成是确定性预报)，使用均方根误差对其进行检验(Armstrong et al, 1992)，均方根误差用于评估预报的误差发散。通过式(6) 和(8) 得到的多个预报(集成预报)，则可以使用Brier技巧评分(Brier Skill Score，BSS)(Bradley et al, 2008)、可靠性曲线(Reliability Diagram)(Hamil, 1997)和百分数评估的方法(刘家骏等，2010)进行检验，具体方法请参考有关文献。

3 结果分析 3.1 条件累积分布的分析和概率预报产品的生成

本文利用根据1981年1月1日到2003年12月31日(共计23年)淮河流域4个子流域内59个气象观测站降水资料计算得到的面雨量，应用式(6) 或(8)，对美国GFS模式24小时降水集合平均预报的日面雨量单值预报进行概率转化，并在转化的基础上生成了具有概率意义的预报产品。以淮河上游大坡岭至息县流域B(图 1)为例。

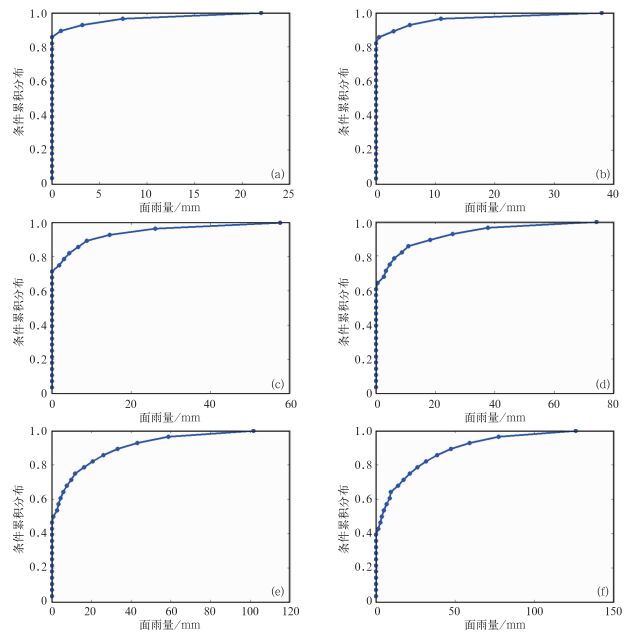
假定在7月，需要预报0.00 mm的日面雨量，在概率区间[0，1]上，给定等距离的28个累积概率分别为1/28，2/28，3/28，…，28/28。因为预报条件x在这里为0.00 mm，则利用式(8) 得到对应的日面雨量预报值为{0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.97，3.23，7.45和21.96 mm}，然后得到在预报条件为0.00 mm条件下的累积分布，图 2a中给出了这28个累积概率。从图中可以看到在单值预报的日面雨量为0.00 mm的条件下，实际日面雨量为0.00 mm的累积概率为0.86，也就是说预报日面雨量为0.00 mm的概率为0.86，那预报日面雨量不为0.00 mm的概率就是(1-0.86)。

对于实际预报，仅仅有预报0.00 mm是不够的，假如需要在淮河上游大坡岭至息县流域预报7月有0.99 mm的日面雨量，同样的在概率区间[0，1]上，给定等距离的28个累积概率分别为1/28，2/28，3/28，…，28/28，利用式(8) 得到对应的日面雨量预报值为{0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.00，0.56，2.99，5.70，10.96和37.95 mm}，然后得到在预报条件为0.99 mm条件下的累积分布(图 2b)。在单值预报的日面雨量为0.99 mm的条件下，实际出现日面雨量为0.00 mm的累积概率为0.82，即预报面雨量为0.00 mm的概率为0.82，预报日面雨量大于0.00 mm的概率为(1-0.82)。类似地，对于需要预报的日面雨量值为5.04、9.67、19.07和30.57 mm的情况，按照单值预报的日面雨量为0.99 mm的情况进行计算求得相应的日面雨量预报值，并得到相应的累积概率(见图 2)。图 2给出的是淮河上游大坡岭至息县流域B(图 1)，由单值预报的日面雨量得到7月的条件累积分布，假定单值预报的面雨量值分别取由0.0、0.99、5.04、9.67、19.07和30.57 mm所生成的条件累积分布，对于全年的其他月份也可以用类似的方法得到，限于篇幅就不赘述。

条件累积分布体现了单值预报存在的不确定性，例如某日面雨量值对应的条件累积概率为0.5时，表示有50%的可能性会出现小于该量值的日面雨量。从图 2a~2f中可以看出，随着需要预报的日面雨量越来越大，实际日面雨量为0.00 mm的条件累积概率就越来越小，即有雨的概率越来越大。此外，需要预报的日面雨量值越大，实际日面雨量出现的量值范围越大。例如需要预报的日面雨量是30.57 mm，从图 2f可以看出，实际日面雨量可能出现的量值范围为0.00~126.03 mm，而需要预报的日面雨量是0.99 mm时，从图 2b可以看出，实际日面雨量可能出现的量值范围为0.00~37.95 mm。这意味着，需要预报的日面雨量越大，实际日面雨量可能出现各种量值范围增大。如果将实际可能出现各种量值的日面雨量作为一个个成员，把它们集成到一起，那么集成预报的发散度越来越大，集成预报包含的可能性就越多。

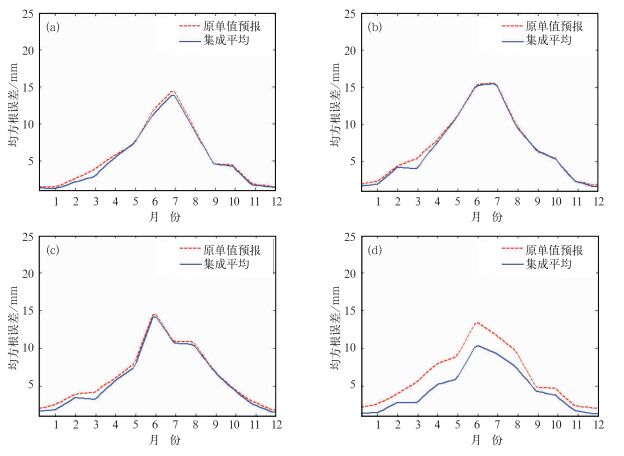
3.2 概率预报产品的集成以及检验分析

从3.1节的分析可以看出，当需要对单值预报中某个量值的日面雨量进行预报时，实际日面雨量会有各种情况出现。例如需要预报日面雨量0.99 mm时，实际出现的日面雨量可能在0.00~37.95 mm之间，且具有不同的概率。也就是说，预报的实际日面雨量包含在0.00~37.95 mm之间。因此这些实际可能出现的一个个量值，可以看做集成预报的一个个“成员”。对于1981年1月1日至2003年12月31日的每一天，GFS在某个流域上预报的日面雨量作为预报条件x，利用式(6) 或(8)，以1/28为累积概率步长，生成28个“成员”，将这28个成员的集成平均作为该流域的预报(为叙述简便，以下简称该方法为新方法)。为考察预报能力是否得到提高，图 3给出了4个子流域以新方法计算的日面雨量集成预报预报值和GFS原始预报的日面雨量均方根误差对比分析。均方根误差本身用于评估预报的误差发散，其值越小越好，从图 3中可以看出，预报误差发散均在夏季大，而冬季小，新方法生成的集成平均预报的日面雨量和GFS原始预报的日面雨量的均方根误差随季节的变化一致。另外分析图 3发现，对于不同季节不同的子流域，由新方法生成的集成平均预报的日面雨量对原始的单值预报日面雨量误差发散度的订正效果均有所不同。由新方法生成的夏季日面雨量集成平均预报对原单值面雨量预报的均方根误差，订正的最大值发生在蚌埠至洪泽湖流域D(图 3d)，夏季订正效果最明显可降低3.11 mm，冬季最小可降低为0.70 mm；而其他地区的订正也很可观，基本上都在0.5 mm以内。例如6月蚌埠至洪泽湖流域D(图 3d)新方法生成的日面雨量集成平均预报的均方根误差最大值为10.36 mm，而GFS日面雨量预报的均方根误差最大值为13.41 mm，均方根误差降低3.05，误差降低非常显著。12月蚌埠至洪泽湖D(图 3d)由新方法生成的日面雨量集成平均预报的均方根误差最小值为1.37 mm，单值面雨量预报的均方根误差最小值为2.08 mm，均方根误差降低0.71。进一步分析GFS日面雨量预报在蚌埠至洪泽湖流域的表现，相对于其他几个子流域，其单值预报明显高于实况，也进一步说明该方法得到的集成预报可能对于单值预报有明显高报的地区，订正效果更为明显。另外，仅从子流域面积大小的变化上并不能看到订正的明显变化，订正效果并不受面积大小的影响。

图 4为利用新方法生成的23年每一天的日面雨量集成预报的Brier技巧评分，通过Brier技巧评分可以评价集成预报对是否发生降水这一事件的预报效果，这里使用气候概率作为参考系统，Brier技巧评分大于0.0就代表技巧有提高，该值越大预报技巧越高，Brier技巧评分等于1.0即是完美预报。图 4的Brier技巧评分显示各个子流域评分均为正，对于降水事件是否发生而言，本文所述方法生成的集成预报技巧均优于气候概率，新方法生成的集成预报具有一定的参考价值。从季节变化上看，Brier技巧评分随季节不同而不同。在冬季的12月到第二年的1和2月期间，枣庄到徐州地区(A)，淮河上游大坡岭至息县流域(B)，洪泽湖以下流域(C)，蚌埠至洪泽湖流域(D)的Brier技巧评分，高的分别能达到0.47、0.56、0.56和0.61，预报技巧均有提高。冬季蚌埠至洪泽湖流域(D)的Brier技巧评分最高，而枣庄到徐州地区(A)最低(图 4)。从图 4中可以看到冬季的Brier技巧评分较高，且蚌埠至洪泽湖流域(D)明显高于其他子流域，可能由于淮河流域冬季的降水影响系统比较简单，降水比较少的原因(图 1b)，GFS模式在冬季的预报技巧较高，在冬季的预报更准确些。而冬季蚌埠至洪泽湖流域(D)的Brier技巧评分较高的原因可能有两个：一方面由于GFS模式的分辨率比较低，蚌埠至洪泽湖流域(D)的空间尺度在这几个流域里与模式的分辨率最为匹配；另一方面由于较低分辨率的模式降水物理过程参数化方案可能更适合较大尺度的流域。从图 4还可以看到，新方法得到的集成预报技巧夏季的没有冬季的高。即便如此，枣庄到徐州地区(A)、淮河上游大坡岭至息县流域(B)、洪泽湖以下流域(C)、蚌埠至洪泽湖流域(D)4个子流域的Brier技巧评分，在夏季的6—8月，最低的Brier技巧评分都能达到0.24、0.16、0.21和0.23，且几个子流域的夏季Brier技巧评分比较接近。与气候概率相比，均有明显的预报技巧。可能的原因一是夏季影响淮河流域降水的天气系统比较多样而且复杂；二是GFS降水的参数化方案无法适合夏季复杂的降水情形。预报技巧较冬季低，所以导致各个子流域日面雨量原单值预报和新方法得到的集成预报技巧也比较低，各个子流域的Brier评分相近。可见，新方法得到的集成预报在不同流域和不同季节的预报技巧是不同的。

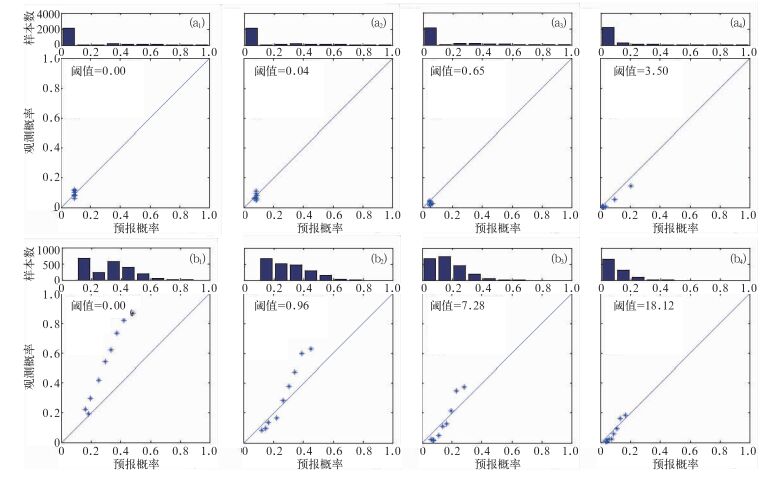
由于Brier评分仅仅是针对了降水概率的技巧进行了评分，无法考虑降水的量级，所以用可靠性曲线和百分位评估来对不同量级降水的效果进行分析。图 5是分淮河上游大坡岭至息县流域冬季和夏季的可靠性曲线图。图 5b₁~5b₄为该子流域夏季(6—8月)的可靠性曲线图，当阈值为0.00 mm时散点明显高于对角线，说明新方法生成的集成预报出现明显的低报。这可能与原GFS预报的分辨率有关，由于原GFS预报分辨率较低，造成对子流域极端天气的预报不足，预报的量级偏小。但随着阈值的逐渐增大，样本集中在预报概率低的一方(见图 5b中上方的直方图)，散点更加靠近对角线。例如对阈值18.12 mm的预报中表现出较好的可靠性，这说明新方法生成的集成预报的大量级日面雨量事件可靠性更高。对比冬季图 5a₁~5a₄和夏季图 5b₁~5b₄发现无论在冬季还是夏季随着降水阈值的增加，散点越接近对角线，日面雨量集成预报的可靠性也随之增大。其他子流域也有类似结果，这里不再赘述。

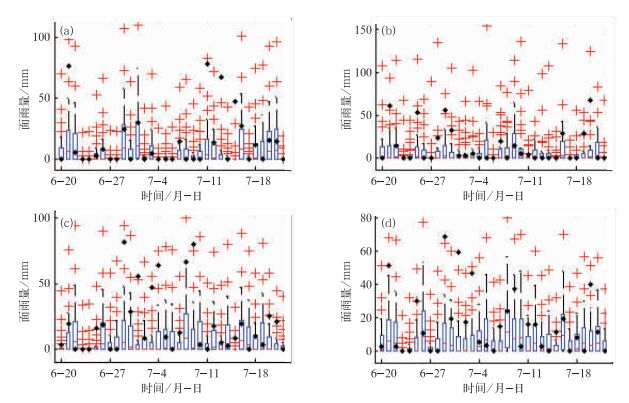
利用2003年6月20日至7月22日淮河流域的一次暴雨过程，对使用条件亚正态分布模型得到的集成预报进行评估。这次暴雨过程淮河流域总降水量普遍有400~600 mm，比常年同期偏多1~2倍，部分站点为历史同期的最大值或次大值。图 6给出盒须图方法的评价，盒须图中盒子两端分别代表上四分位数和下四分位数，中间横线为中位数，须线两端分别为Q₁-1.5IQR(Q₁为下四分位数，IQR=Q₃-Q₁为四分位距)和Q₃+1.5IQR(Q₃为上四分位数)的值，小于Q₁-1.5IQR或大于Q₃+1.5IQR的值被定义为异常值。从图 6中可以发现，这次的极端降水天气过程中，大部分的观测值都落在了盒须图的须线内，只有少数落在异常值范围内，这些落于异常值范围的点均为面雨量比较大的事件，大多都在30 mm以上(大到暴雨以上的量级)。其他3个流域也有类似情况，新方法生成的集成预报对小量级日面雨量事件的预报效果较好，对于30 mm以上量级的降水预报则预报不足。

4 结论和讨论

本文主要介绍了一种利用长时间序列的观测和模式(单值)预报的历史数据，建立概率预报的方法。采用1981年1月1日至2003年12月31日淮河流域59个气象站点的降水观测资料，以及同时段的美国GFS单值预报，建立条件亚正态分布函数的概率预报模型，得到单值预报的条件下观测出现的概率分布，再在此基础上形成集成预报，得到的集成预报量化了单值预报不确定性，同时还对原来GFS单值预报起到一定的误差订正作用。将该方法应用于淮河流域的4个面积不同的子流域，通过分析得到以下结论：

(1) 从由淮河上游大坡岭至息县流域7月不同单值预报的日面雨量得到的条件累积分布的分析来看，由小量级日面雨量得到的概率预报发散度相对较低；随着单值预报的日面雨量值的增加，得到的概率预报的发散度不断增大，不确定性也加大。

(2) 采用均方根误差对模型处理产生的集成平均预报进行检验的结果表明：在误差发散度的订正方面，模型产生的集成平均对不同子流域单值预报的订正均有正效果，且程度各不相同，蚌埠至洪泽湖流域的订正效果最为显著，模型产生的日面雨量集成平均在6月的均方根误差减小得最为明显，可减小3.11 mm。

(3)4个子流域通过该模型得到的集成预报的Brier技巧评分总是大于0的，说明4个子流域的集成预报对是否降水这一事件的预报都比气候概率更好。4个子流域Brier技巧评分最小值分别为0.24、0.16、0.21和0.23，最大值分别为0.47、0.56、0.56和0.61，说明集成预报在整年的时间段上都具有一定参考价值。

(4) 夏季淮河上游大坡岭至息县流域的集成预报在可靠性曲线上显示出一定程度的低报。当实际日面雨量阈值为0.00~7.82 mm时，预报出现不同程度的低报，但随着降水阈值的增加，低报情况好转，可靠性曲线越来越接近对角线，在对实际日面雨量阈值为18.12 mm的预报中表现出较好的可靠性。不管是冬季还是夏季集成预报的可靠性都是逐渐增加的。

(5) 从百分位评估的个例中看出，集成预报对小量级面雨量的预报效果更好，对于30 mm以上的面雨量预报能力则逐渐减弱。

总的来说，本文所述的新方法能生成比较可信的面雨量集成预报，由其处理得到的面雨量集成平均相对原GFS模式的单一预报而言，在部分流域有一定程度的订正效果和提高。同时集成预报效果随着原单值预报技巧的变化而变化；当原单值预报技巧高时，相应的集成预报技巧也就更高；而当预报技巧较低时，集成预报技巧也变低，说明这种方法产生的集成预报依赖原单值预报的预报效果。在降水概率预报中，集成预报优于气候概率，同时集成预报的可靠性也随着预报阈值的增加而增强。需指出的是，本文所用的GFS模式格点资料代表的是以该格点为中心的2.5°×2.5°的范围内的面雨量，即可能存在模式预报格点代表的面积和流域面积空间尺度不匹配的问题，这可能会造成GFS模式面雨量预报技巧降低。对于此类问题，在今后的研究中，可以通过选择更高分辨率的数值模式预报作进一步研究。

除GFS模式分辨率的影响之外，GFS模式面雨量预报技巧还受到模式中的某些物理过程参数化方案的影响，GFS模式是美国的模式，它的某些物理过程参数化方案可能对于美国地区更加适合，然而东亚的青藏高原大地形、下垫面以及降水的物理参数化过程等与美国不一样，这可能使得GFS模式一些物理过程参数化方案并不一定适用于东亚的降水过程。尽管如此，本文所描述的方法生成的集成预报仍使数值预报的技巧提高，说明基于观测和预报的历史资料建立的条件亚正态分布模型，对于提高模式的预报技巧是一条可行的路子。