2. 宁夏大气探测技术保障中心,银川 750002
2. Meteorological Observation and Technology Support Centre of Ningxia, Yinchuan 750002
省级气象计量检定机构的风速实验室承担了各省气象行业风速仪表的量值传递工作,其标准风速值的准确与否直接影响被检仪表的使用。近年来,有一些关于风速仪器检定方面的研究,主要针对风速检定中的阻塞系数修正(李国森等,2006),检定结果的不确定度分析(朱乐坤等,2006;黄蕊等,2011)以及风速自动化检定的设计与实现。还有一些风速资料在实际应用方面的论文(苑跃等,2011;曹丽娟等,2010;邹立尧等,2010;郭凤霞等,2010),都与风速测量值的准确与否有密切的联系。
在2011年3—9月的西北区域气象计量检定实验室比对工作中发现,风速实验室的比对结果令人不是很满意,几个实验室比对结果相差较大,分析发现除了风洞本身的原因外,主要是由于实验室的环境条件影响和JJG431-86检定规程(国家质量技术监督局,1986)中空气密度修正系数查算表过于粗略造成的。
1 实测风速值的计算根据JJG483-86检定规程,标准风速的数值是根据数字微压计与皮托管连接,读取实测风压值,通过式(1) 的计算得到实测风速值。
| $ v = k{v_1} $ | (1) |
式中,v为实测风速(单位:m·s-1); v1为相当风速,由式(2) 计算(单位:m·s-1);k为总修正系数,由式(3) 计算。
| $ {v_1} = 1.278\sqrt {{p_v}} $ | (2) |
式中,pv为微压计在各检定点上的读数平均值分别减去初始零位读数得到的实测风压值(单位:Pa)。
| $ k = {k_\rho }\sqrt {{r_t}\xi {k_c}} $ | (3) |
式中:kρ为空气密度修正系数,由式(4) 计算;rt为微压计工作液体密度修正系数,由于目前使用数字微压计,故rt=1;ξ为皮托管系数;kc为微压计系数,采用二等补偿式微压计时,kc=1。
| $ {k_\rho } = \sqrt {\frac{{1013.25\left({273.15 + t} \right)}}{{288.15\left({p - 0.378u\;{e_w}} \right)}}} $ | (4) |
式中,t为实验室空气温度(单位:℃);p为大气压力(单位:hPa);u为实验室空气的相对湿度(单位:%);ew为空气温度为t℃时的饱和水汽压(单位:hPa)。
根据式(1)~(4),可推导出实测标准风速值的计算公式,见式(5)。
| $ v = 1.278\sqrt {\frac{{1013.25\left({273.15 + t} \right)}}{{288.15\left({p - 0.378u\;{e_w}} \right)}}{p_v}\xi } $ | (5) |
通过式(5) 可以看出,对标准风速测量值的影响量有微压计读数pv、皮托管系数ξ及风速实验室的空气温度t、大气压力p和空气湿度u。
2 各变化量对标准风速测量值的影响分析由于皮托管系数是由上一级计量检定给出的数值,且稳定、变化量很小,故对风速测量值的影响可忽略不计。对风速测量值影响较大的有微压计、实验室空气温度、大气压力及空气湿度。
2.1 微压计误差以目前各省使用的Mensor2500型数字微压计为例,其准确度等级为0.01级,最大允许误差为0.25 Pa。根据JJG431-86检定规程,微压计误差对各检定点的影响量如图 1和图 2所示。
|
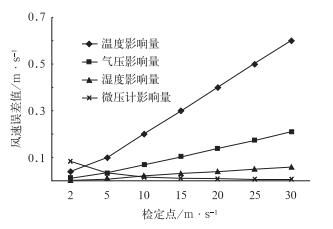
图 1 以“10”为间隔时对标准风速测量值影响量的变化曲线 Fig. 1 The changing curves of influence factors on measured values of standard wind speed at the interval of '10' |
|
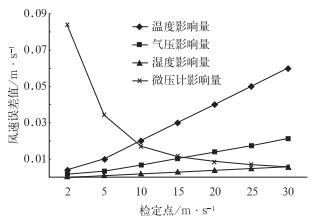
图 2 以“1”为间隔时对标准风速测量值影响量的变化曲线 Fig. 2 The changing curves of influence factors on measured values of standard wind speed at the interval of '1' |
根据式(4) 和(5),空气密度修正系数主要与风速实验室的空气温度t、大气压力p、空气湿度u和饱和水汽压有关,饱和水汽压影响量很小,可忽略不计。JJG431-86检定规程中,绘制了空气密度修正系数查算表(略),查算表列举了以空气温度、大气压力、空气湿度各以“10”为间隔的空气密度修正系数,查算表中空气温度、大气压力、空气湿度对风速值的影响量如图 1所示。可以看出:
(1) 实验室空气温度的变化对标准风速值的影响量最大,在最大风速30 m·s-1时为0.6 m·s-1。
(2) 大气压力对标准风速值的影响量也较大,微压计和空气湿度的影响量较小,都小于0.1 m·s-1。
(3) 除微压计外,在实际工作中查算空气密度修正系数表时,以查算区间的中间点为分界线,故中间点的误差量为最大,也就是图 1中温度、气压、湿度各误差值的一半,也就是在风速30 m·s-1检定点时标准风速误差量为0.3 m·s-1。
根据式(5),以实验室空气温度、大气压力、空气湿度各以“1”为间隔进行计算的各变化量对风速值的影响量如图 2所示。可以看出:
(1) 微压计误差和实验室空气温度、大气压力、空气湿度的各变化量对标准风速的影响量均小于0.1 m·s-1。
(2) 除微压计外,在实际工作中以检定前和检定结束时,分别读取实验室空气温度、大气压力和空气湿度数值的平均值计算风速值,故风速实验室检定1台风速表前后的温度变化不应超过3℃,大气压力变化不应超过5 hPa,相对湿度变化不应超过10%。
2.3 比较分析通过图 1查表和图 2公式计算的风速误差结果进行比较分析发现:
(1) 微压计对检定结果影响只限于本身误差的大小,而与查算表和公式计算没有直接联系。
(2) 相对湿度在查表和公式计算中对风速结果影响均较小。
(3) 气压在查表和公式计算中对风速结果影响较大,且随着风速的增大而增大,在30 m·s-1时两者之差为0.19 m·s-1,是不可忽略的。
(4) 温度在查表和公式计算中对风速结果影响很大,且随着风速的增大而增大,在30 m·s-1时两者之差为0.54 m·s-1,远远超过了风速检定装置复现性误差要求的0.20 m·s-1的要求,需要加以控制。
通过以上比较和分析,查表和公式计算两者结果相差较大,由于查算表是由公式计算编制的,故用公式计算的数值更接近于标准风速的真值,因此在处理检定结果时应该用公式计算较为准确。
风速实验室的温度和气压对风速检定结果的影响大,需要对其进行控制。但是气压值相对较为稳定,一般实验室都能满足气压的变化量5 hPa的要求;主要是对实验室的温度加以控制,使其在1台风速表前后的实验室温度变化不应超过3℃,即公式计算中风速变化量不超过0.18 m·s-1,而在实际计算中取检定前后两次温度的算术平均值,故风速的误差值最大为0.09 m·s-1,完全能够满足风速检定装置的误差要求。
2.4 实例分析用一台样表分别在4和8月在风速实验室中进行检定,检定后标准风速的数值分别以式(5) 进行计算和依据JJG483-86检定规程中的空气密度修正系数查算表进行计算,分别得到不同的数据如表 1所示。
|
|
表 1 不同状态条件下标准风速值(单位:m·s-1) Table 1 The standard wind speed values under the conditions of different atmospheric states (unit: m·s-1) |
从表 1中可以看出:
(1) 用式(5) 计算的标准风速值与用JJG483-86检定规程中的空气密度修正系数查算表进行计算的风速值相差较大,最大为0.22 m·s-1,超过了风速检定装置复现性误差要求的0.20 m·s-1的要求。
(2) 两次检定的环境条件大气压力和空气湿度相近,对标准风速的结果影响不大。影响最大的是实验室空气温度,4月实验室气温值为22.2℃,在空气密度修正系数查算表中应查20℃时的数值,而8月实验室气温值为25.7℃,在空气密度修正系数查算表中应查30℃时的数值,两者取舍相反,故用查算表计算的标准风速值前者偏小,后者偏大。
(3) 随着检定点风速值的增大,用式(5) 计算的标准风速值与用JJG431-86检定规程中的空气密度修正系数查算表进行计算的风速值的误差值也增大。
3 结论与讨论(1) 实验室空气温度的变化对标准风速值的影响最大,故检定1台风速表前后的实验室温度变化不应超过3℃。
(2) 大气压力的变化对标准风速值的影响较大,但是气压值相对较为稳定,一般实验室都能满足气压的变化量。
(3) 空气湿度的变化对标准风速值的影响较小,一般实验室都能满足要求。
(4) 微压计必须按照检定周期进行送检,只要准确度等级优于0.01级,量程在0~2500 Pa之内的数字微压计,其误差量对标准风速值的影响可忽略。
(5) JJG431-86检定规程中的查算表过于粗略,按照此查算表计算的标准风速值误差较大,在30 m·s-1检定点最大可达到0.3 m·s-1,超过了风速检定装置复现性误差要求的0.20 m·s-1的要求。目前计算机都很普及,利用公式进行计算的数值既准确又方便,可以不必再利用查算表进行计算,造成不必要的误差。
曹丽娟, 鞠晓慧, 刘小宁, 2010. PMFT方法对我国年平均风速的均一性检验[J]. 气象, 36(10): 52-56. DOI:10.7519/j.issn.1000-0526.2010.10.008 |
郭凤霞, 朱文越, 饶瑞中, 2010. 非均一地形近地层风速廓线特点及粗糙度的研究[J]. 气象, 36(6): 90-94. DOI:10.7519/j.issn.1000-0526.2010.06.014 |
国家质量技术监督局, 1986. 国家计量检定规程JJG431-86 DEM6型轻便三杯风向风速表检定规程[M]. 北京: 中国计量出版社.
|
黄蕊, 党选发, 宋媛, 2011. 风速检定装置不确定度的评定[J]. 气象水文海洋仪器, 28(3): 28-30. |
李国森, 敖振浪, 2006. 风速仪在风洞检定中的阻塞修正[J]. 气象, 32(9): 67-70. DOI:10.7519/j.issn.1000-0526.2006.09.011 |
苑跃, 赵晓莉, 王英, 等, 2011. 自动与人工观测风速和风向的差异分析[J]. 气象, 37(4): 490-496. DOI:10.7519/j.issn.1000-0526.2011.04.014 |
朱乐坤, 郑丽春, 2006. 自动气象站各要素传感器检定结果的不确定度分析[J]. 应用气象学报, 17(5): 635-642. DOI:10.11898/1001-7313.20060507 |
邹立尧, 国世友, 王冀, 等, 2010. 1961—2004年黑龙江省近地层风速变化趋势分析[J]. 气象, 36(10): 67-71. DOI:10.7519/j.issn.1000-0526.2010.10.011 |
 2013, Vol. 39
2013, Vol. 39 