引言

风电场风速在三种时间尺度上的波动可以对风力发电产生影响，其中超短期波动(几分钟)对风电机组的控制有一定影响；短期波动(几小时到几天)对风电并网和电网调度有影响；而中长期波动(数周或数月)与风电场或电网的检修维护计划有关, 本文重点关注风电场超短期(短临)风速的预报问题。但由于风速受多种要素影响，具有很强的随机性和非稳定性，是最难预报的气象要素之一。因此，风速的超短期(短临)预报成为风电场亟需解决的技术难题之一。

国家能源局要求所有已并网运行的风电场应在2012年1月1日前建立起风电预报体系并开始试运行。该预报体系要求并网风电场每15 min滚动上报未来15 min至4 h的短临风电功率预报数据。国家能源局这一技术规定使得15 min滚动预报的未来0~4 h短临风速预报成为迫切需要解决的预报技术热点。

目前，风电场的短临风速预报模型主要有时间序列模型和智能模型两大类，而每种预报方法都各有优缺点及适用范围(高阳等，2010; 方艳莹等，2012；王美玖等，2010)。智能模型中的神经网络法(范高峰等，2008；蔡敏等，2009；钱莉等，2010)通过大量的学习和训练来建立关系，对复杂问题的求解十分有效；模糊逻辑法(熊浩等，2007；黄文杰等，2010)则通常要与其他方法配合使用以达到预报目的；支持向量机(杜颖等，2008；曾杰等，2009)也是典型的智能模型之一。而时间序列模型是风电预报的一种常用方法(Taylor et al, 2009; 高文元等，2009)，其中持续法(吴国呖等，2005)将最近一点的风速观测值作为下一点的预报值, 对于平稳变化的低频信号具有较好的预报精度；更高级的时间序列模型则包括自回归滑动平均(ARMA)(彭跃华等，2009；洪翠等，2011)、卡尔曼滤波(冬雷等，2007；潘迪长等，2008)等，其中ARMA模型是自回归模型(AR)和滑动平均模型(MA)的有机结合，也是目前最为成熟、使用最广的时间序列分析方法。

上述的时间序列模型在制作多步预报时，预报值会趋于平均值，且往往对极值的拟合效果欠佳。为克服以上不足，本文给出了时间序列的均值生成函数，视其为原序列生成的、体现各种长度周期性的基函数。在基函数基础上，构造了一种均生函数预报模型，既可以进行多步预报，又可以较好地预报极值。

风电场短临风速预报的精度不仅与预报方法有关，还与预报周期和所预报地点的风速特性有关。一般而言，预测周期越短，预报地点的风速变化越缓和，预报误差就会越小，反之，预报误差越大(Sanchez, 2006)。目前风电场短期风速预测的绝对平均误差为25%~40%(Bossanyi, 1985; 陶玉飞等，2009)，而采用时间序列法预测风电场短期风速的误差可小于10%(丁明等，2005)。

本文拟在测风塔观测数据的基础上，建立一套基于均生函数的未来0~4 h精细化风速预报模型，并定量对比该模型与传统的ARMA模型的预报效果，以达到理论建模应用于实际的目的。

1 数据和建模方法 1.1 数据简介

以河北张家口崇礼坝顶(地形较复杂)和内蒙古锡林浩特市达布希勒特苏木(地势相对平坦)两个测风塔的70 m实测风速数据为研究对象。在时间上，选取2011年1、4、7和10月的风速数据，分别代表冬、春、夏、秋四个季节的变化特征。该测风塔数据序列为每10 min采样一点，为满足风电场短临风电预报业务需求(即提供未来0~4 h，15 min间隔的风速预报结果)，将原始风速序列中10和20时的风速平均插值到15时，40和50时平均插值到45时，其余时刻风速不变，从而得到15 min间隔的风速序列，即每天共有24×4=96个采样点。

首先以坝顶测风塔数据为建模对象，建立风电场风速短时临近预报模型，之后将建模理念拓展应用至锡林浩特市的测风塔风速数据中，以检验该模型在空间上的适用性。

1.2 基于均生函数的预报模型

所构造的基于均生函数的预报模型主要由三部分组成，即序列的延拓均生函数、通过灰色关联度挑选出的优势周期、优势周期与预报序列之间的多元回归模型。

1.2.1 均值生成函数

设一时间序列x(n)的均值为$\bar x = \frac{1}{n}\sum\limits_{i = 1}^n {x\left(i \right)} $，对于时间序列x(n)定义均生函数

$ \begin{array}{l} {{\bar x}_l}\left(i \right) = \frac{1}{{{n_l}}}\sum\limits_{j = 0}^{{n_i} - 1} {x\left({i + jl} \right)}, \\ \;\;\;i = 1, \cdots, l;\;\;\;1 \le l \le m \end{array} $

(1)

式中, n_l=INT(n/l)，且根据适用情况，取m=INT(n/3)。根据式(1)，可以得到m个均生函数。由此可见，均生函数是由时间序列按一定的时间间隔计算均值而派生出来的。将均生函数定义域延拓到整个数轴上，即作周期性延拓，即可得到均生函数延拓序列，它是一种周期性函数(魏凤英，2007)，在一定程度上代表了原序列的各种不同周期变化。

1.2.2 灰色关联度分析

灰色关联度分析方法是根据要素之间发展趋势的相似或相异程度，作为衡量要素间关联程度的一种方法。灰色系统理论提出了对各个子系统进行灰色关联度分析的概念，力图透过一定方法，寻求系统中各子系统(或要素)之间的数值关系，非常适合动态历程分析。利用此方法目的在于揭示均生函数与预报序列关系的强弱程度，其操作对象是要素的时间序列，最终结果表现为均生函数与预报序列之间的关联度大小，即关联度。其基本步骤如下(李春霞等，1996)。

1.2.2.1 序列标准化处理

为保持不同因子的量纲统一性，首先对各个序列的要素进行标准化处理，用来消除不同序列绝对值大小相差悬殊带来的不可公度性：

$ {x_i}\left(k \right) = \frac{{x\left(k \right) - \overline {{x_i}} }}{{{s_i}}} $

(2)

式中，k=1, 2, 3, …, m，为各序列长度；i=1, 2, 3, …, n，为序列个数，即因子数与目标量之和；x(k)为原始序列，${\overline {{x_i}} }$为该序列的平均值，s_i为该序列的标准差，x_i(k)为标准化处理的结果。

1.2.2.2 关联系数计算

对于因子x_i对目标量x₀在k点的关联系数可以用如下公式计算：

$ {\xi _i}\left(k \right) = \frac{{\mathop {\min }\limits_i \mathop {\min }\limits_k \left| {{x_0}\left(k \right) - {x_i}\left(k \right)} \right| + P\mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{x_0}\left(k \right) - {x_i}\left(k \right)} \right|}}{{\left| {{x_0}\left(k \right) - {x_i}\left(k \right)} \right| + P\mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{x_0}\left(k \right) - {x_i}\left(k \right)} \right|}} $

(3)

其中，P为分辨系数，其值在0~1之间，不同的P值对应不同的关联度，理论证明，P值越小，分辨率越高，一般可取0.5(邓聚龙，1987)。

1.2.2.3 关联度计算

因为每一列数据都有n个长度，因此，按照式(3) 计算出来的关联系数也就有n个，信息过于分散。将上述关联系数取平均，就可把各点关联系数集中为一个值，即关联度：

$ {\gamma _i} = \frac{1}{n}\sum\limits_{k = 1}^n {{\xi _i}\left(k \right)} $

(4)

1.2.3 多元线性回归建立预测模型

通过灰色关联分析挑选出优势周期后，利用多元线性回归方法建立预报模型。设模型将用作q步预报，将入选的均生函数作q步外延，则得到最终的均生函数预报方程：

$ \hat x\left({n + q} \right) = {a_0} + \sum\limits_{i = 1}^k {{a_i}{f_i}} \left({n + q} \right)\;\;\;q = 1, 2, \cdots $

(5)

式中, a₀和a_i为多元回归技术估计的系数，f_i为延拓均生函数。

1.3 自回归滑动平均模型(ARMA)

ARMA模型由自回归项和滑动平均项两部分组成，一般描述的是平稳时间序列。选择Pandit-Wu S.M法进行时间序列的分析建模，因此在模型定阶时用ARMA(P, P-1)(P=2, 3, 4, …)模型取代ARMA(P, q)(P=2, 3, 4, …; q=1, 2, 3, …)模型来进行逐步拟合(潘迪夫等，2008；李建康，1994)，同时，选择最小信息准则(Akaike information criterion, AIC)进行模型定阶。AIC函数为：

$ AIC = \frac{{2L}}{n} + \frac{{2\left({p + q + 1} \right)}}{n} $

(6)

式中，L是对数似然值，n是观测值数目。AIC准则要求AIC的取值越小越好。即AIC值达到最小的模型被认定是最佳模型。

2 建立预测模型及模型预报效果检验

分别针对河北坝顶测风塔1、4、7和10月的实测风速数据，进行建模，并对未来0~4 h的短时临近风速进行精细化预报。在建模之前，需要对原始的风速序列进行平稳化处理。

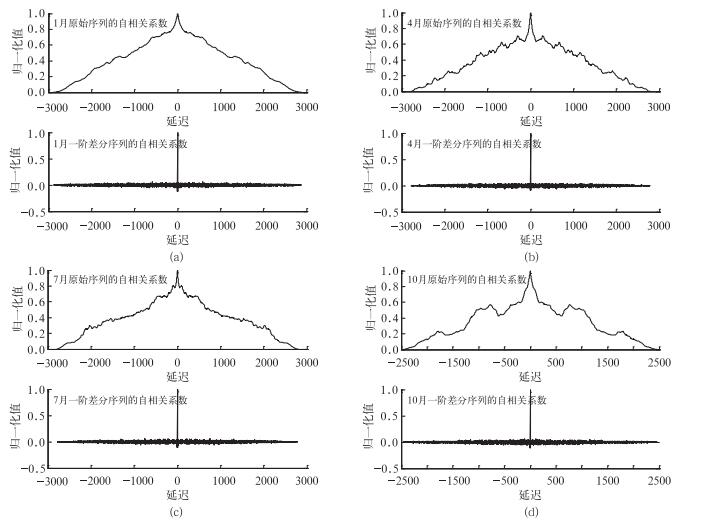
2.1 风速序列的平稳化

图 1给了2011年4个典型月份河北坝顶测风塔风速序列自相关分析结果, 横坐标为延迟期，可见：原始序列的自相关系数不能快速衰减为零，可推断原始风速序列的随机性大，是随时间变化的非平稳序列。这种非平稳性在用预报模型预报风速时会产生较大的影响，因此，可以在原始样本数据进行训练前对数据进行平稳化处理。对原始序列进行差分处理，一阶差分处理后数据的自相关系数接近0，且当延迟期为2时，其自相关系数都与0有差异，即典型月份风速的一阶差分序列是随机稳定序列(图 1)。因此，采用一阶差分方法来减少风速数据的非平稳性。

2.2 均生函数预报模型的建立

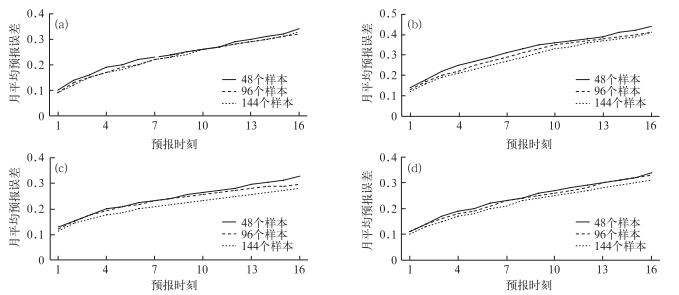
以风速的一阶差分序列作为研究对象，建立预报模型，首先需要确定预报模型的各个参数，包括拟合样本个数、优势周期个数等。首先指出，所建预测模型是一种针对站点、针对预报时刻的动态模型，模型中涉及的所有参数都是随站点和起报时刻不断变化的，具有较强的适应性和实用性，而以下所有结果的分析都基于该动态预报模型逐时刻，即15 min滚动预报结果而进行的。图 2给出月平均尺度上，利用不同拟合样本数的预报模型对未来0~4 h、15 min间隔的风速预报误差对比，横坐标为预报的1~16个时刻。从图中可见，拟合样本数为96(1 d)时，模型预报误差小于拟合样本数为48的模型误差，大于拟合样本数为144的模型误差，但大部分情况下(1、4和10月)其差别不大，说明拟合样本数越大，拟合效果越好。研究中为方便对比，选取一天整周期，即96个拟合样本点进行建模。

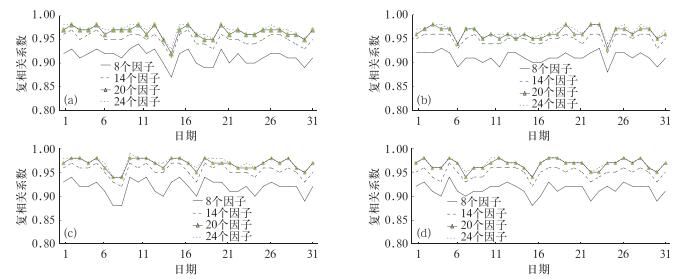
同时，图 3给出了4个典型月份中，96个拟合样本模型情况下，不同优势周期(回归因子)个数的预报模型的复相关系数变化情况，横坐标为日期。图中可见，优势周期个数越大，拟合效果越好，当优势周期(回归因子)个数取20时，预报模型的复相关系数较大，且基本都大于0.96，说明该模型拟合效果极佳。因此，均生函数预报模型的基本参数选取如下：拟合样本个数为96，优势周期个数为20，预报未来16个时刻(即0~4 h)的风速。

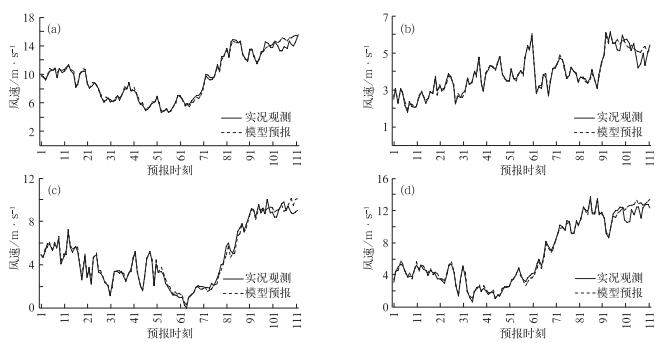
利用上述均生函数预报模型，对河北坝顶2011年1、4、7和10月的风速序列进行逐时刻动态建模和滚动预报，图 4给出了4个典型月份的模拟、预报效果对比情况，图中横坐标表示时刻点，第1~96个时刻点为模型拟合区间，第97~112个时刻点代表模型对临近16个时刻的预报区间。图中可见，模型在4个典型月份的某些时刻点的模拟效果较好，模型预报的相对误差可小于10%，同时模型在对风速序列的极值点的模拟方面比其他时间序列分析方法有明显优势。

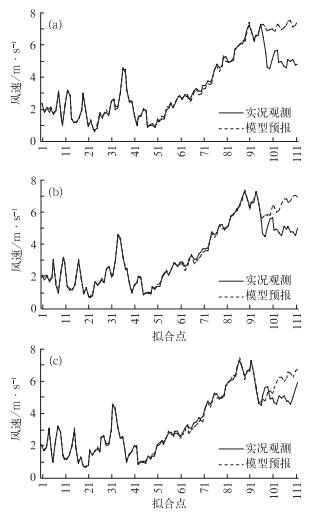
受制于统计模型本身对转折性信息描述的不足，均生函数模型在个别点的表现欠佳(图 5a)。例如，实况天气监测显示2011年1月2日16时至1月3日06时(第1~56个拟合点区间)，河北坝顶受偏南风控制，风速较小，基本维持在2 m·s^-1左右。06时之后，坝顶风向转为偏北风，风速逐渐增大，临近预报时刻(即第96个拟合点)风速最大超过7 m·s^-1，且出现随机震荡，从不断增加突转为逐渐减小，与模型拟合区间内的风速变化出现显著不同的特征，因此，模型预报风速与实况观测风速出现较大差异(图 5a)。若将模型的拟合时段顺序向后滚动，使得拟合时段内包含一定量的风速震荡信息，则模型预报效果就会有明显的改善(图 5b和5c)。综上所述，均生函数模型对短临风速预报具有较好的预报能力，即使在某些个别转折点的预报表现欠佳，仍可通过实时向后滚动预报的技术进行动态订正，从而取得较好的预报效果。

2.3 误差分析

为了定量考察预测的精度，对预测模型采取如下误差指标进行分析：

相对误差：$\varepsilon = \frac{{\hat x - x}}{x} \times 100\% $

式中，${\hat x}$为通过模型预测出的风速数值，x为对应时刻实际测量的风速值。

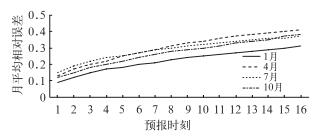
表 1给出了月平均尺度上，均生函数预测模型对未来0~4 h(16个预报时刻)的预报误差特征。为了进一步分析模型在不同风速区间的预报能力，对比了原始序列、＜3 m·s^-1风速序列(切入风速)、≥3 m·s^-1风速序列和＞12 m·s^-1风速序列(额定风速)的误差分布情况。表中可见，模型对大风区间的预报效果明显好于小风区间的预报效果，尤其在小于切入风速(3 m·s^-1)的小风区间内，模型的预报表现不好。但当风速超过切入风速(3 m·s^-1)或者额定风速(12 m·s^-1)后，该模型的预报效果明显提高，说明模型对风电场风机正常运行情况下的短临风速具有更好的预报能力。图 6中横坐标为模型预报的未来16个时刻，图中可见，1、4、7和10月，该模型的预报误差范围分别为9%~31%，13%~41%，15%~37%和12%~38%，可见，模型在冬半年的预报表现明显好于夏半年。

从逐日变化情况来看(图略)，均生函数模型的预报能力表现出一定的波动性，即在某天，模型预报的日平均误差接近10%，而个别日期，其预报的日平均误差则超过40%。这种不稳定的预报特征可能与天气形势的转折有关。但总体而言，该模型的预报表现较好。

为了进一步对比均生函数模型与传统的ARMA模型的预报效果，在相同拟合样本数和预报时效条件下，建立了ARMA模型。按照2.3节中所述的AIC准则，对ARMA模型进行定阶。表 2给出了4个典型月份不同模型阶数所对应的AIC值。从表中可见，ARMA(2，1) 模型的AIC值最小，故根据AIC准则函数的意义可知，ARMA(2，1) 模型为最适用于一阶差分的风速序列的模型。

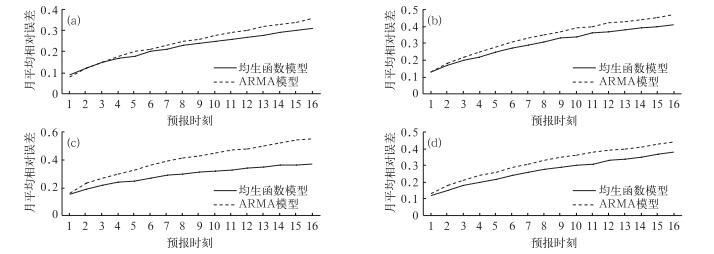
图 7给出了两种预报模型对0~4 h短临风速预报的月平均误差对比情况，横坐标为模型预报的未来16个时刻。图中可见，在所有4个典型月份中，均生函数模型在短临预报时效的所有预报时刻上的预报误差明显小于传统的ARMA模型。均生函数模型在1、4、7和10月的月平均相对误差分别为22.2%、30.1%、29.1%和27%，明显低于ARMA方法的月平均预报误差(24.4%、33.9%、39.9%和31.9%)，预报效果有显著提高。综上所述，所建立的基于均生函数的风速短临预报模型的预报效果明显好于传统的ARMA方法，在实际业务预报中具有重要的应用价值。

3 预报模型推广应用

为检验均生函数模型在空间上的适用性，将上述建模思路和理念应用至内蒙古地区，根据内蒙古锡林浩特市达布希勒特苏木测风塔2011年1、4、7和10月的实测风速特点，确定了该地区均生函数预测模型的各个动态参数。图 8给出了均生函数模型预测对上述4个典型月份风速预测的月平均误差对比，横坐标为模型预报的未来16个时刻。图中可见，所建立的均生函数预测模型对于内蒙古达布希勒特苏木测风塔未来0~4 h中的大部分预报时刻的月平均相对误差小于35%，且冬半年比夏半年的预报效果更好，总体预报效果基本令人满意，说明该预报模型在空间上也具有较好的适用性。

4 小结

利用河北张家口崇礼坝顶测风塔的70 m实测风速数据，采用均生函数、灰色关联度和多元回归等统计预报方法，建立了一套15 min动态滚动的未来0~4 h风速短临预报模型，并定量对比该模型与传统的ARMA模型的预报效果。之后将建模理念拓展应用至内蒙古锡林浩特市的测风塔风速数据中，以检验该模型在空间上的适用性。结果表明：

(1) 均生函数模型在对风速序列的极值点的拟和方面比其他时间序列分析方法有明显优势；个别转折点的预报表现欠佳，可通过实时向后滚动预报的技术进行动态订正。

(2) 误差统计可知，均生函数预测模型在河北坝顶风电场2011年1、4、7和10月的月平均相对误差分别为22.2%、30.1%、29.1%和27%，比传统的ARMA模型分别减小了2.2%、3.8%、10.8%和4.9%，取得了较高的预报准确率。

(3) 所建立的均生函数预测模型在内蒙古达布希勒特苏木地区的总体预报效果基本令人满意，说明该预报模型在空间上也具有较好的适用性。

短临预报模型的预报值比较平稳，对转折性风速预报误差较大，可通过滚动向后预报或集合模式预报结果等方法进行改善。在大部分数据点处能给出比较令人满意的结果，具有一定的业务应用价值。同时，本研究中的误差分析仅基于96个拟合样本、20个优势周期的均生函数模型进行而得出的，实际应用中延长拟合样本个数和优势周期个数对模型进行局部调整，也可进一步显著提高模型的预报精度。