引言

估测降水量一直是广大气象工作者和研究人员十分关注的热点问题，由于产生降水的因素很多，加上观测站点稀疏，造成估测降水的难度较大。用卫星资料进行降水估测，国外专家进行了深入研究，取得了很大的成就，Adler等(1984)应用一维云模式建立对流核心的云顶亮温与降水率和降水面积之间的关系；Goldenberg等(1990)应用一维云模式方法进行MONEX试验期间降水估测；Li等(1993)分别对白天和晚上的云图分类, 找出对流核心后建立核心云顶亮温与降水量、降水面积之间的关系；以Arkin等(1994)提出的方法为代表的云指数法以其简单方便的优点, 被广泛应用于气候研究，以Scofiled提出的方法为代表的云生命史法, 不仅考虑了云顶温度与降水的关系, 也考虑了云的发展变化与降水的关系, 被用于强对流云团的降水估计中；Goodman等(1994)进行了非线性反演估测。在国内，很多专家对降水估测研究也取得了一定成就，刘晓阳等(2010)利用多种雨量计校准雷达降水的方法，生成1 h降水分布，校准雨量计数量和估测精度有明显正相关；梁卫芳等(2008)对顺序卡尔曼滤波校准法进行定量估测降水，在稳定性天气过程中，校准效果最好；王建林等(2008)釆用变分技术校准方法进行雷达定量估测降水，1 h估测降水误差明显减少；卢乃锰等(1998)应用MS24红外资料详细分析了云顶亮温等与云的降水强度之间的关系；杨扬等(1995)使用云分类和降水率估计方法获取面雨量；王华荣等(2008)运用最低红外亮温和红外亮温增量因子对地面1 h降水估测；李腹广等(2007)利用Z-R关系对黔西南地区降水进行估测；师春香等(2001)运用卫星资料采用神经网络方法对日面降水量进行估测；熊秋芬等(2003)用神经网络方法利用卫星多通道资料对淮河区域一次暴雨过程进行降水估测；段旭等(2009)用Z-I关系得出的雷达反演降水资料与中国气象局下发的6 h降水资料，建立联合降水量估测场，采用变分方法对其进行同化，得出云南6 h降水估测；郑媛媛等(2004)利用雷达资料建立不同期气候区域的Z-I关系；闵爱荣等(2007)利用卫星和雷达资料联合估计大暴雨，卫星估测降水在很大程度上弥补了雷达估测降水在空间上的不足。在以往的研究中主要使用基本反射率因子资料，或者是卫星云顶量温(Temperature of Brightness Blackbody，TBB)资料，采用经验方法及逐步回归分析方法构造降水估计方程，所采用的估测降水技术是基于统计和经验的降水反演，由于降水是一个复杂的物理过程，地面降水与气象要素变量之间存在非线性关系，具有很多的不确定性，因此用统计方法构造的降水方程存在一定局限性。

本研究应用卫星和雷达资料，采用BP神经网络建立单站预报模型、云分类Z-I关系和传统Z-I关系对距昆明雷达站大于20 km、小于150 km区域且2008年建有自动站的18个站点进行了降水估测，一方面研究雷达卫星的综合应用及定量应用，一方面引入卫星资料对降水估测中的误差问题进行改善。

1 资料

本文应用的卫星资料有TBB、云顶亮温梯度、水汽云图、总云量、云分类，还有雷达基本反射率因子资料、云南省自动雨量站1 h降水资料。资料时间是2008、2009和2010年5—10月，其中雷达资料是6 min间隔的体扫资料，其他均是逐小时资料。由于雷达资料的数据量较大，在资料收集及处理上工作量较大，因此只选用昆明雷达站数据进行研究，另外雷达数据存在静锥区，对距昆明雷达站大于20 km、小于150 km区域内的测站进行研究，再加上用到测站历史逐时降水资料，本研究对2008年已建有自动雨量站的18个测站进行降水估测研究。资料处理是将卫星和雷达资料插值到18个测站上。

(1) 云分类、总云量是读取最靠近测站的格点数据值作为测站的云型和云量云分类、总云量的产品范围：FY2C为50°S~50°N、55°~155°E, FY2D为60°S~60°N、27°~147°E(许健民等，2008)。

(2) TBB资料和水汽云图资料是通过Gressmam插值得到测站数据(段旭等，2009)，插值半径为0.071°。TBB产品范围为45°~165°E(FY2C), 27°~147°E(FY2D), 60°S~60°N(许健民等，2008)；水汽云图为MICAPS 13类数据格式。

(3) 云顶亮温梯度资料是用TBB资料，根据式(1) 求得, 其中，G为云顶亮温梯度，T为云顶亮温，i、j为图像坐标。将云顶亮温梯度数据进行Gressmam插值得到测站数据，插值半径为0.071°。

$ \begin{array}{l} G = \left\{ {{{[T(i + 1, j) - T(i - 1, j)]}^2} + } \right.\\ \;\;\;\;\;\;{\left. {{{[T(i, j + 1) - T(i, j - 1)]}^2}} \right\}^{1/2}} \end{array} $

(1)

(4) 自动雨量站资料为逐小时雨量资料，资料处理是将1 h降水量进行3 h累加，处理成3 h降水资料。小时降水量资料均要通过界限值检查、时间一致性检查和空间一致性检查，界限值检查使用区域界限值检查，纬度大于25°N的站点界限值为125 mm·h^-1, 纬度小于25°N的站点界限值为150 mm·h^-1(任芝花等，2010；段旭等，2009)。

(5) 雷达基本反射率因子资料，首先对多普勒雷达回波图像进行中值滤波处理，达到既去除噪声又保护图像边缘的效果，中值滤波的基本原理是把数字图像或数字系列中一点的值用该点的一个邻域中各点值的中值代替，中值的定义如下：

一组数x₁，x₂，x₃，…，x_n，把n个数按值的大小顺序排列：

x_i1≤x_i2≤x_i3≤…≤x_in

$ \begin{array}{l} y = {\rm{Med}}\left\{ {{x_1}{x_2}, {x_3}, \cdots, {x_n}} \right\} = \\ \;\;\;\;\;\;\;\left\{ \begin{array}{l} {x_{i\left({\frac{{n + 1}}{2}} \right)}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n为奇数\\ \frac{1}{2}\left[ {{x_{i\left({\frac{n}{2}} \right)}} + {x_{i\left({\frac{{n + 1}}{2}} \right)}}} \right]\;\;\;\;\;\;\;\;\;\;n为偶数 \end{array} \right. \end{array} $

(2)

y称为序列x₁，x₂，x₃，…，x_n的中值(段旭等，2009)。

读取一个体扫资料中的组合反射率因子，即取体扫资料在垂直高度上的最大反射率因子，把最大反射率因子数据由极坐标数据格式转换为以雷达站为原点的直角坐标系数据格式，经过Gressmam插值将数据插值到18个测站上，扫描半径为5 km，得到测站反射率因子数据。

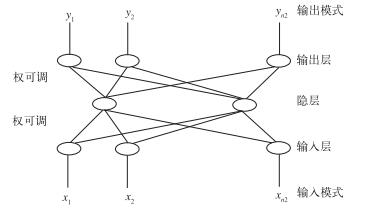
2 方法 2.1 BP神经网络模型

人工神经网络(Artificial Neural Networks, ANN)，一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型，是一个可以提取一组预报变量和另一组自变量之间非线性关系的数据处理系统，建立的网络为人工神经网络的训练过程，是用自适应算法递归迭代求解因变量与自变量之间的非线性关系。训练后的神经网络模型可以来估测或预报估测变量。到目前为止，人工神经网络模型已达上百种，BP神经网络模型是典型的多层网格包括输入层、隐层和输出层，层与层之间采用全互连方式，图 1给出了一个BP网络结构模型(段婧等，2005)。

网络中神经元的输入是上一层神经元输出的权重和：${n_j} = \sum\limits_j {{w_{ij}}{\delta _j}} $，由网络神经元活化函数(一般为sigmoid函数)将权重和转换为神经元输出，δ_j=1/[1+exp(-n+θ_j)]，其中，θ_j为常数，在训练过程中，可进行权重调整，Δw_ij(n+1)=η(δ_jo_j)+αΔw_ij(n)，其中Δw_ij(n+1) 是连接神经元i和j的权重被修改后的值，o_j是误差修正项，η是学习率，α是动量项。

神经网格实现了多层网格学习的设想，当给定网格一个输入模式时，它由输入层单元传到隐层单元，经隐层单元逐层处理后再送到输出层单元，由输出层单元处理后产生一个输出模式，这是一个逐层状态更新的过程，称为前向传播。若输出与期望输出模式有误差且误差不满足要求时，误差转入后向传播过程，将误差值沿连接通路逐层传送并修正各层连接权值，这就是误差后向传播的涵义，用给定的一组训练模式，重复对网格训练，也就是重复前向传播和误差后向传播的过程，当各个训练模式都满足要求时，多层前馈人工神经网络学习过程结束，并保留一组连接权重系数，已训练好的神经网络模型可以对新的输入模式给出判别结果。

选取雷达基本反射率因子、TBB、云顶亮温梯度、水汽云图、卫星云分类产品和卫星云总量产品6种资料，采用BP神经网络建立单站预报模型，对滇中地区18个测站进行3 h降水估测。样本总共3240个，采用3000个做训练样本，时间是从2008年5月1日00时至2010年6月27日19时，240个做检验样本，时间是从2010年6月27日00时至7月4日10时、2010年7月19日19时至7月24日16时。通过多次训练，对训练参数进行修改，根据样本输入及训练效果，构造的网络结构为6-13-1的降水估计BP神经网络模型，神经网络模型中输入的变量为6个，隐含层神经元为13个，输出变量为1个。神经网络训练参数采用训练次数为100，两次显示之间的训练步数为25，训练目标为0。根据训练好的测站模型，当向模型输入变量时，模型给出测站降水估测结果。

2.2 传统Z-I关系

$ {Z_{昆明}} = 198.6{I^{1.65}} $

(3)

式(3) 引用文献(段旭等，2009)的研究，式中I为雨强, Z值首先是测站使用Gressmam插值得到站点dBz值，再通过公式：dBz=10lgZ计算得出。根据公式(3) 可以计算得到测站在雷达一个观测时次的雨强I，根据式(4) 时段降水量与雨强的关系(施丹平，2001)，对计算出的雨强再进行时间积分得到时段估测降水量，然后对3 h内雷达所有估测降水量进行累加，得到测站3 h降水估测值。

$ R = \int\limits_1^{{t_2}} {I{\rm{d}}t} $

(4)

式中，R为3 h估测降水量，I为雨强，t₂为观测时间。

2.3 云分类Z-I关系

在云分类数据中，有0、1、11、12、13、14、15和21数据类型，分别为晴空海面、晴空陆地、混合像元、高层云或雨层云、卷层云、密卷云、积雨云、层积云或高积云8个云型数据，其中混合像元为低云、中云和高云的混合云型。云分类数据中的晴空海面及晴空陆地，在云分类数据生成原理中，利用红外1通道亮温、水汽通道亮温及红外通道2亮温等资料，采用多特征阈值方法，把云和晴空分开(梁卫芳等，2008)，在出现晴空海面及晴空陆地的区域，在雷达回波上没有降水回波出现，在地面上也就没有降水，另外卷层云和密卷云都不是降水云，本文只对其他的4种云型进行降水估测研究。利用雷达反射率因子、卫星云分类产品及自动雨量站3 h降水资料各4200个样本，时间是从2008年5月1日00时至2010年8月23日19时，分别统计出测站出现4个云型对应的样本系列。在这4200样本中，混合像元有1450个样本，高层云或雨层云有42个样本，卷层云有794个样本，密卷云有155个样本，积雨云有69个样本，层积云或高积云有1278个样本, 得到4个类型的降水序列。

Z-I关系建立，假定一个Z-I关系式为Z=AI^b，分别对4个云型降水序列进行最优化处理，根据2.2节传统Z-I关系估测降水方法计算估测降水量。参数A的取值范围为50~270，步进为0.1，参数b的取值范围为0.9~1.7，步进为0.01，调整A、b参数分别对6个类型的降水序列进行最优化处理，当式(5) 中CTF最小时, 确定A和b值。

$ CTF = \min \left\{ {\sum\limits_i {\left[ {{{\left({{A_i} - {G_i}} \right)}^2} + \left({{A_i} - {G_i}} \right)} \right]} } \right\} $

(5)

式中，A为3 h估测降水量，G_i为3 h实测降水量。通过对4个类型的降水序列进行最优化处理，分别建立了4组Z-I关系。表 1是4种云型Z-I关系估测降水与实测降水的均方根误差，其中高层云或雨层云关系估测降水的均方根误差大于4 mm，层积云或高积云Z-I关系估测降水的均方根误差在2 mm左右，另外两种云型估测降水的均方根误差小于1 mm。

$ \begin{array}{l} 混合像元:Z = 180{I^{1.5}}\\ 雨层云:Z = 160{I^{1.1}}\\ 积雨云:Z = 178{I^{1.6}}\\ 层积云:Z = 170{I^{1.4}} \end{array} $

(6)

在实际业务运用中，读取测站雷达反射率因子值及该时次的云型数据，通过dBz=10lgZ计算出Z值，把Z值代入相应云型的关系式中进行计算，逐一计算出3 h内的雨强，再进行累加得到测站3 h降水估测值。

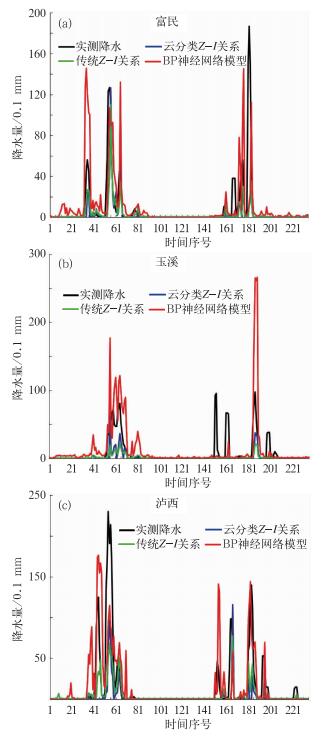
3 估测降水分析 3.1 实况降水与估测降水比较

图 2是18个测站利用BP神经网络建立单站预报模型、云分类Z-I关系和传统Z-I关系对240个样本的降水估测图, 选取3个作为示例，其他测站图略。可以分析出用BP神经网络建立单站预报模型估测降水在几个方面优于另外两种方法。

首先，对18个测站估测降水曲线进行分析，用BP神经网络建立单站预报模型估测的降水，比另外两种方法估测的降水更接近实测降水。其次对于降水量大于25 mm的估测，用BP神经网络模型估测降水量误差比另外两种方法减小了5~10 mm，寻甸站在样本中最大降水量为87.9 mm，传统Z-I关系、云分类Z-I关系及BP神经网络建立单站预报模型3种方法估测降水依次为4.1、18.1和28.8 mm，澄江出现66.5 mm降水，3种方法估测降水量依次为10.7、12.8和15.5 mm，楚雄出现25.7 mm降水，3种方法估测降水依次为1.7、2.7和8.7 mm, 沾益出现35.9 mm降水，3种方法估测降水依次为2.9、3.9和8 mm。另外对于小于25 mm的降水，对于测站样本中最大降水的估测，用BP神经网络建立单站预报模型估测的降水误差在1~2 mm之间，比如富民站，实测最大降水12.7mm，估测降水为11 mm，误差为1.7 mm；安宁站，实测降水5.5 mm，估测降水3.9 mm，误差1.6 mm；宜良站，实测降水18.7 mm，估测降水20 mm，误差为1.3 mm；武定站，实测降水4 mm，估测降水4.4 mm，误差0.4 mm，像这样的测站还有玉溪、马龙、陆良、弥勒、通海和石屏，而用另外两种方法估测的降水误差都大于2 mm，有的站点在10 mm以上，如富民、马龙、陆良、弥勒、泸西和石屏。最后用BP神经网络建立单站预报模型估测的降水，比另外两种方法估测在降水空报率上有所降低，7月2—4日，滇中地区没有产生降水，用传统Z-I关系和云分类Z-I关系就估测出了降水，而用BP神经网络建立单站预报模型没有估测出降水，像安宁、澄江、武定、禄劝、楚雄、元谋等测站。

虽然，用BP神经网络建立单站预报模型估测的降水在一些方面优于另外两种方法，但是从18个测站的估测降水分析图上可以看出，此方法出现了估测降水量明显大于实测降水的情况(图 2)。

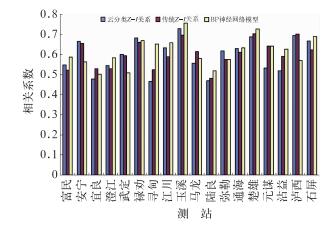
3.2 实测降水与估测降水的相关系数

图 3分别是传统Z-I关系、云分类Z-I关系及BP神经网络模型的3 h估测降水量与实测降水量的相关系数图，所有相关系数都通过0.05显著性水平检验。用BP神经网络模型估测的降水量与实测降水量的相关系数有5个测站(寻甸、玉溪、楚雄、沾益和石屏)明显大于另外两种相关系数。

3.3 实测降水与估测降水的均方根误差

用云分类Z-I关系估测降水的均方根误差，比用传统Z-I关系估测降水的均方根误差略有减小，但减小幅度不是很大(图 4)。用BP神经网络模型估测降水的均方根误差仅有寻甸、通海、石屏站减小，其他站反而增加，这与3.1节中的分析相对应，主要是BP神经网络模型估测的降水出现一些时次明显大于实测降水造成的。

表 2为3种方法对18个测站中不同降水量级的估算降水均方根误差平均值，从表中可用看出，对于大于25 mm的4个测站，用BP神经网络模型比用云分类Z-I关系减小了0.6 mm。对小于25 mm降水的测站的均方根误差平均，比用云分类Z-I关系估算的多了0.3 mm。但是从18个测站均方根误差平均值看，云分类Z-I关系和BP神经网络模型估算的相接近。

3.4 BP神经网络模型估测降水误差原因分析

估测降水与实测降水存在误差是所有估测方法无法回避的问题，进行误差原因分析对估测方法的改进有重要的作用，BP神经网络模型估测降水方法，是利用样本资料，通过网络训练建立模型，进行降水估测。造成估测降水与实测降水存在误差有以下原因：

(1) 样本数据代表性不强。BP神经网络模型是通过样本数据初始化后，进行网格训练建立的，样本数据能否全方面表示出产生降水的信号来，对BP神经网络模型估测降水的精度有一定的影响。本研究只应用了2008—2010年5—10月资料，由于资料有限，样本资料不能全部表示站点产生降水的特征，是影响估测效果的一个原因。

(2) 卫星和雷达数据不能全部表示降水的特征。由于降水是一个复杂的过程，涉及多个气象要素和非气象要素，仅用卫星和雷达资料不能全方面地表示产生降水的特征。

(3) 在样本的匹配上，包括时间尺度、空间尺度也可能会影响到最终的结果。

4 结论

本文使用BP神经网络建立单站预报模型、云分类Z-I关系和传统Z-I关系，利用基本反射率因子、TBB、云顶亮温梯度、水汽云图、卫星云分类产品、卫星云总量产品及自动站降水资料，对云南滇中区域2008年已建有自动站的18个站点进行3 h降水估测研究，通过研究，得到了如下结论：

(1) 云分类Z-I关系的研究中，引入卫星云图中的云分类产品资料，对Z-I关系估测降水能力有一定提高，用云分类Z-I关系估测降水的均方根误差，比用传统Z-I关系估测降水的均方根误差略有减小。

(2) 使用BP神经网络建立单站预报模型，3 h降水估测能很好地表示降水产生的趋势，准确地表示出降水的增强和减弱特征，对于强降水估测比另外两种方法估测的降水误差小。用BP神经网络建立单站预报模型估测的降水，比另外两种方法估测在降水空报率上有所降低。

(3) 综合利用卫星和雷达资料，利用BP神经网络建立单站的预报模型，在一定程度上解决了空报和误差问题，对强降水估测能力有所提高，但还是出现了一定的空报和误差，在以后的研究中有待改善提高。