2. 国家气象中心/数值预报中心,北京 100081;
3. 新疆气象台,乌鲁木齐 830002
2. Numerical Prediction Centre, National Meteorological Centre, Beijing 100081;
3. Xinjiang Meteorological Observatory, Urumqi 830002
众所周知,积云对流过程是大气中重要的过程,它通过感热、潜热和动量输送等反馈作用影响大尺度环流,并在决定大气温度、湿度场的垂直结构中起着关键的作用,也影响大众最为关心的降水预报。由于数值模式分辨率的限制,一般数值模式中要求对积云对流过程进行参数化。由于现有模式的模拟结果对积云对流参数化方案的选择极为敏感,研究积云参数化方案对提高模式性能有重要意义。
积云参数化方案的评价研究是积云参数化方案研究的重要内容,它为积云参数化方案的应用、改进和研发提供依据。评价积云参数化方案的研究方法主要有三种,第一种是完全预报法,即是采用一般的数值模式给定初始场和边界条件进行积分,将积分结果跟观测比较。这种方法是评价积云参数化方案的最基本方法,但是,这种评价方法的缺点也是明显的。在完整的数值模式积分过程中,不仅包含了初始场和边界条件的误差,也包含模式动力过程、其他物理过程参数化方案造成的误差,因此无法将结果优劣完全归因于积云参数化方案(Lord, 1982)。第二种方法是半预报方法(Lord, 1982; Ramanathan, 1980),即在某一给定观测时间,由观测估计的大尺度平流项、地表通量和辐射加热等变量驱动积云参数化方案,将获得的降水、视热源和视湿汇等变量跟观测相比较,来判断积云参数化方案的优劣。半预报方案的优点是明显的,不包含模式动力过程产生误差,也没有其他物理过程参数化方案造成的误差,因此方便诊断检查积云参数化方案问题所在。第三种方法是使用单柱模式进行评价,单柱模式(Single Column Model,SCM),由Betts等(1986)提出,是只有一个维度(垂直方向)的模式,相当于数值模式中的一个格点柱,但同时又可以独立于数值模式的其他部分,其预报方程为
| $ \frac{{\partial A}}{{\partial t}} = \frac{{\partial A}}{{\partial t}}{\left| {_{{\rm{LS}}} + \frac{{\partial A}}{{\partial t}}} \right|_{{\rm{PHY}}}} $ |
其中,A表示水平动量、位温和水汽混合比等预报变量,下标LS表示由观测给定的随时间变化的大尺度强迫项,下标PHY表示物理过程参数化方案产生的倾向项。因此,单柱模式在积分时,不仅要由观测提供大尺度热力和动力初始条件,也要由观测提供随时间变化的大尺度强迫项。利用单柱模式评价的方法,与完全预报方法相比,不需要考虑物理过程对大尺度动力过程反馈作用,不包含在完整模式中动力过程产生的误差;与半预报方法相比,因单柱模式可以包含一整套物理过程,可以方便地考察积云参数化方案与其他物理过程的耦合情况。显然,利用单柱模式进行评价的方法是介于完全预报和半预报之间的方法。目前,国内对积云参数化方案的评价方法主要采用完全预报方法(王建捷等,2001;徐国强等,2005),这主要是因为一方面这些研究更注重为积云参数化方案的应用方面服务,而较少着重于对积云参数化方案的改进或研制研究,另一方面也是因为使用半预报方法和单柱模式对资料质量要求较高,不易获取。
我国自主研发的GRAPES模式在实际业务中表现良好,值得进一步发展(熊秋芬,2011;纪永明等,2011;陈超君等,2012)。杨军丽等(2012)基于GRAPES全球模式建立了单柱模式(GRAPES_SCM),该单柱模式性能良好,可用于检验和改进GRAPES模式中各种物理过程参数化方案,从而最终提升GRAPES模式性能。因此本文采用该单柱模式,利用GCSS WG4第三次个例模拟所用资料(Krueger et al, 1999),对GRAPES模式中的Betts-Miller-Janjic方案(Betts et al, 1986; Janjic, 1994)、Kain-Fritsch eta方案(Kain et al, 1990; Kain, 2004)和Simplified Arakawa-Schubert方案(Arakawa et al, 1974; Grell, 1993)进行数值试验分析,评价各方案的优缺点,并据此对Kain-Fritsch eta方案进行修改,将修改后的方案放入单柱模式和GRAPES_meso模式(陈德辉等,2008;徐国强等,2008)进行检验,以期得到有正效果的修改方案。
1 积云参数化方案简介 1.1 Betts-Miller-Janjic方案(简称BMJ方案)该方案是由Betts-Miller方案改进而来。Betts-Miller方案是一种成熟的对流调整方案,其深对流采用修正的湿绝热线,浅对流则采用混合线作为最初猜想的对流调整参考廓线,然后再根据深对流湿静态能守恒,浅对流无降雨发生等制约条件对初始参考廓线调整得出最终的对流参考廓线。Janjic(1994)为了解决Betts-Miller方案在实际应用中的一些问题,对Betts-Miller方案进行改进,形成所谓的Betts-Miller-Janjic方案。相对Betts-Miller方案,该方案主要修改有:(1) 引入无量纲参数云效(cloud efficiency)来表示对流组织性质,云效取决于熵的变化、降水量和云的平均温度。深对流参考廓线和松弛调整时间都根据云效的变化而变化;(2) 浅对流湿度参考廓线则保证熵的变化最小且非负。
1.2 Kain-Fritsch eta方案(简称KFeta方案)Kain-Fristch eta方案是Kain-Fritsch方案的改进版本。Kain-Fritsch方案采用深对流在一定时间内消耗大部分(约90%)对流有效位能的假定作为闭合假设,采用一个简单一维云模式来计算积云对流对网格尺度的反馈效应。该云模式包含湿上升流和湿下沉气流,还包含相对简单的微物理过程。通过浮力分类机制来决定上升气流与环境的双向质量交换(卷入和卷出),这是Kain-Fritsch方案的一大特征。KFeta方案对Kain-Fritsch方案主要改进包括:引入浅对流过程、设定夹卷率下限和修改下沉气流部分。
1.3 Simplified Arakawa-Schubert方案(简称SAS方案)该方案是Grell(1993)根据Arakawa-Schubert方案(Arakawa et al, 1974)简化修改而成的。在SAS方案中不再采用在一个格点中存在理想云谱的假定,而是将之简化成只允许一种云存在(即深对流或者浅对流)的假定。深对流包含上升气流和下沉气流,采用准平衡假设作为闭合假设,分为动力控制部分、静力控制部分和反馈部分。静力控制部分主要包含云模式,计算云的热力性质;动力控制部分决定对流的位置和大小;反馈部分则决定加热和减湿的垂直分布。
2 数值试验设计 2.1 资料单柱模式所用的资料为(Global Energy and Water Cycle Experiment Cloud System Study Working Group 4,GCSS WG4) 第三次个例模拟所用资料。该资料来自(Atmospheric Radiation Measurement Program,ARM计划)美国南部大平原地区(观测场地中心位于36.61°N、97.49°W)1997年夏季的(Intensive Observing Period,IOP,6月18日23:30至7月17日23:30 UTC)。该观测数据集提供了包括局地对流和频繁大雨天气以及受大尺度对流和持续降水混合影响的天气在内的中纬度夏季天气过程事件(Cederwall et al, 1999),非常适合用于评价积云参数化方案性能的研究。
2.2 试验设计本文所用的单柱模式跟文献(杨军丽等,2012)中所用单柱模式基本一致,只是Exner气压变量设置稍有差别,与原来Exner气压变量在积分过程中保持不变不同,在本文中Exner气压变量在3000 m高度以下为模式变量诊断所得。
辐射方案采用RRTMG,微物理方案采用WSM6,边界层方案采用MRF,陆面方案采用CoLM,不同的试验除了采用不同积云参数化方案外,其他配置相同。
为了减少积分误差,参照文献(杨军丽等,2012),分为4个子时间段进行模拟。子时间段1对应的时间分别为世界时6月22日23:30至6月26日23:30,子时间段2对应的时间为6月26日23:30至30日23:30,子时间段3对应的时间为7月7日23:30至12日23:30,子时间段4对应的时间为7月12日23:30至17日23:30。
与文献(杨军丽等,2012)类似,为了克服单柱模式对初始条件的敏感性,各个子时间段的初始场由对应时间的观测给定后,通过在大气边界层(本研究取为2 km)内用标准差为0.5 K的位温的随机序列扰动和标准差为0.5 g·kg-1的水汽混合比的随机序列扰动对位温和水汽混合比的初始场进行扰动,这样可以得到多个不同初始场的样本,但本文采用的扰动为伪随机序列扰动,这样既保证了初始场的随机性,又保证了不同试验对应样本初始场的一致。各个试验结果为20个样本的平均。
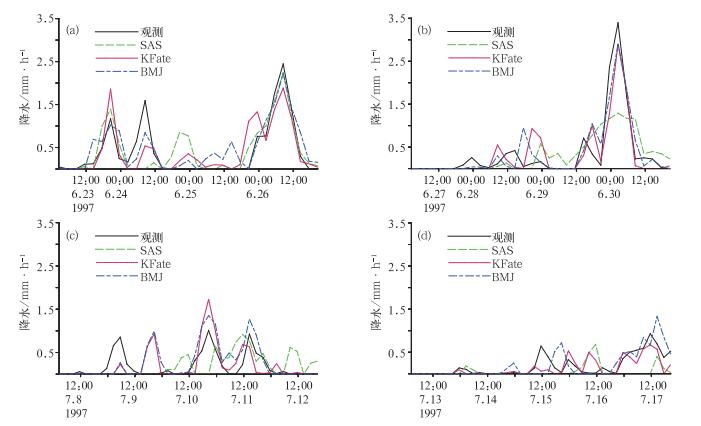
3 结果分析 3.1 降水分析降水是评价积云参数化方案性能的重要参数之一,因此下面先看不同积云参数化方案模拟降水情况。子时间段1主要经历了3次降水过程,其中第三次最强,达到2.5 mm·h-1。从图 1a可以看出,KFeta和BMJ方案都很好地模拟出子时间段1的3个降水事件,而SAS方案则没有模拟出子时间段1的第二个降水事件,随后还模拟出了1 mm·h-1左右的虚假降水。子时间段2经历了2弱1强的降水过程,对于子时间段2的强降水过程,KFeta和BMJ方案模拟的降水都跟观测非常的接近,达到3 mm·h-1,而SAS方案模拟的降水则明显小于观测,不到1.5 mm·h-1。子时间段3主要经历了3个强度相当的降水过程,强度在1 mm·h-1左右,KFeta和BMJ方案都能较好地模拟出后两个降水过程,但是第一个降水过程则模拟的强度过小,且启动较慢,随后还模拟出了强度为1 mm·h-1的虚假降水,SAS方案则完全没有模拟出第一次降水过程。对于子时间段4,KFeta方案模拟的效果比较好,能模拟出这个时间段主要降水特征,而SAS方案模拟的降水明显偏小。
|
图 1 不同积云参数化方案对子时间段1~4的降水模拟(a~d,单位:mm·h-1) Fig. 1 Time series of rainfall (a-d, unit: mm·h-1) for subcases 1-4 with different cumulus parameterization schemes |
表 1给出了不同方案在4个子时间段内产生的累积降水。可以看出,BMJ方案倾向于产生比观测多的降水,比如子时间段1观测的累积降水为37.24 mm,而BMJ模拟为44.6 mm,子时间段3观测的累积降水为20.86 mm,BMJ方案则为31.48 mm。KFeta方案产生的累积降水量则跟观测值大致相当。SAS方案则在子时间段4模拟的降水严重偏小,只有8.75 mm,跟观测相差约12 mm。
|
|
表 1 累积降水(单位:mm) Table 1 Accumulated rainfall in simulation and observation (unit: mm) |
表 2给出了4个子时间段不同方案模拟降水和观测的相关系数和均方根误差。可以看出,除了SAS方案在子时间段3和4模拟的降水的相关系数达不到显著相关外,其他方案在4个子时间段中模拟降水的相关系数都通过了0.001的显著性检验。
|
|
表 2 模拟的降水与观测的相关系数和均方根误差 Table 2 The correlation coefficients and root-mean-square error (RMSE) of simulated rainfall with observation |
从上面的分析可以看出,不同方案对子时间段1和2的降水模拟的效果好,而子时间段3和4的相对较差。这可能与子时间段3和4观测区域的平均大尺度强迫不能很好地反映典型的强对流复合体的热力结构特征有关(Xie et al, 2002)。当然,除了大尺度条件的不适当外,SAS方案在子时间段3和4模拟的降水较差还可能与其激发机制有关,需要更进一步的探讨。
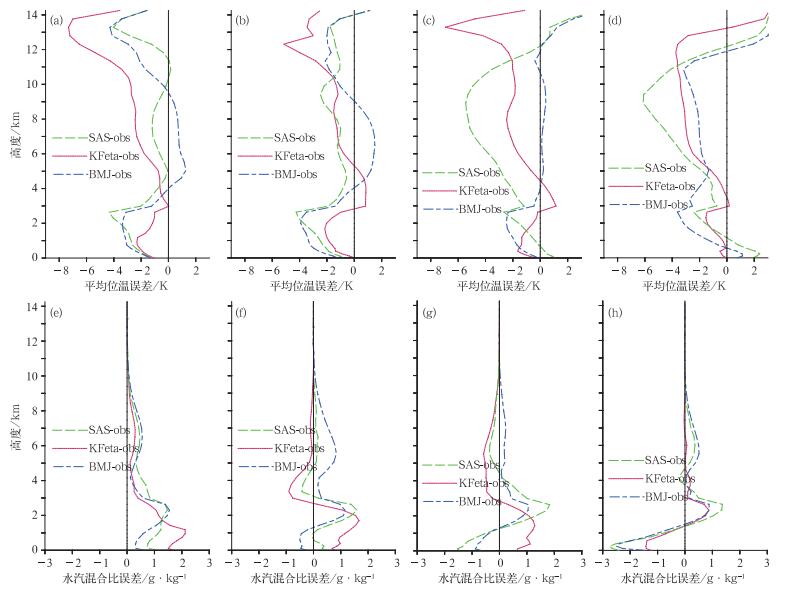
3.2 位温和水汽混合比误差分析积云参数化方案的主要目的就是在条件允许的情况下(积云参数化方案被激发),通过调整温湿廓线,形成降水,消除(或减弱)条件不稳定。因此积云参数化方案对大气的温湿廓线必然有重要的影响。图 2给出了时间平均位温和水汽混合比误差的垂直廓线。总的来看,不同方案的平均位温误差幅度在-8~8 K内,水汽平均误差在低层最大,但也在-3~3 g·kg-1范围内,在10 km以上高度水汽误差接近于零,这些结果与文献(Arakawa et al, 1974)类似。
|
图 2 不同积云参数化方案子时间段1~4的时间平均位温误差(a~d, 单位:K)和水汽混合比误差(e~h, 单位:g·kg-1)的垂直廓线 Fig. 2 Profiles of time-averaged potential temperature errors (a-d, unit: K) and water vapor mixing ratio errors (e-h, unit: g·kg-1) for subcases 1-4 of different cumulus parameterization schemes |
从图 2可以看出,BMJ试验在子时间段1~3模拟的位温在4 km高度以下偏冷,幅度可以达到-4~-2 K之间,在4~9 km高度之间则误差较小,主要表现为偏暖,特别是在子时间段3,BMJ方案模拟的位温在4~10 km之间平均误差接近于零。在子时间段4,BMJ试验模拟的位温在0.5 km高度以下存在着浅薄的偏暖层,在0.5~11 km之间则表现为偏冷,误差的极大值在2~3 km高度处,接近-4 K。从湿度误差来看,BMJ试验在子时间段2~4表现为低层偏干,在子时间段1则偏湿,但相比于其他方案偏湿幅度最小。BMJ试验在4个子时间段在1.5 km高度以上都表现为偏湿,这体现了BMJ方案具有较强的水汽垂直输送能力。从BMJ试验模拟温湿误差垂直结构(低层偏冷偏干,中高层偏暖偏湿)可以看出,与实际观测相比,经BMJ方案调整的大气层过于稳定。
KFeta试验模拟的位温总体表现为偏冷,在10 km高度以下误差较小,3 km高度以下位温误差相比其他方案最小,但是在12~14 km处则总是比其他两个方案偏冷,造成较大的误差。在湿度上,我们还很容易看出KFeta试验相对于其他试验对流层低层偏湿,只有在子时间段4偏干,但其偏干的幅度依然小于BMJ和SAS试验。
SAS试验在子时间段1和2位温误差相对小,整层主要表现为偏冷,但是后两个子时间段模拟的位温在对流层7~9 km高度处偏冷严重,误差可以达到-6 K左右,低层则偏暖。SAS试验在子时间段1和2主要表现为偏湿,后两子时间段在1.5 km高度以下都偏干,其中在子时间段4湿度误差达到了-2.5 g·kg-1。SAS方案在子时间段4的激发不足与低层偏干和SAS方案激发机制有很大关系。与其他两方案相比,SAS方案在激发机制上的特点是既限制了自由对流层与气块起始层之间高度差,同时也考虑了上升气块对云下空气较为强烈的卷夹作用,因此SAS方案在对流层低层偏干环境中激发则更为吃力。
从上面分析可以得出,不同的积云参数化方案可以产生很不相同大气温湿误差廓线,其中BMJ方案模拟的大气层结过于稳定,低层偏冷偏干,中高层则偏湿;KFeta方案则表现为高层偏冷,低层偏冷偏湿,但低层偏冷的程度小于BMJ方案。KFeta和BMJ方案这些性能似乎能够在一定程度上说明在许多台风模拟研究中(Li et al, 2009; Davis et al, 2002; Deshpande et al, 2010)发现使用KFeta(或者KF)方案模拟的台风要强于使用BMJ方案模拟的台风强度的原因:与KFeta方案相比,BMJ方案使得台风环境气层低层更加倾向于偏冷偏干,不利于台风的加深发展。Liu等(2001)利用Tropical Ocean Global Atmosphere Coupled Ocean-Atmosphere Response Experiment(TOGA CORE)的观测资料同样发现了KF方案产生类似的误差,即高层偏冷,低层偏湿。对于KFeta方案这些性能,我们后面还要做一些相对深入的分析。
3.3 视热源和视湿汇分析视热源Q1主要是由辐射加热率、水汽的净凝结产生的潜热和涡动垂直输送感热造成,而视湿汇Q2则是由水汽的净凝结和水汽的涡动垂直输送水汽造成。当大气中存在对流活动时,可以较好地用这两个变量考察积云对流对大尺度环境温度和湿度的反馈作用。
为了简化起见,下面只分析子时间段2。图 3给出了子时间段2各个试验Q1和Q2的时间平均值,以及积云参数化方案对Q1和Q2贡献部分Q1c和Q2c廓线图(分别由积云参数化方案对模式反馈的温度和湿度倾向所求得)。由图 3可以看出,在子时间段2中,不同方案模拟的Q1在400 hPa附近达到最大,可以达到4 K·d-1左右,与观测的值都相当接近,这主要是由于大尺度平流项都是由观测给定的,同时也可以看出,不同方案模拟的Q1比观测的Q1稍微小,这说明了模拟的位温相对观测相对偏冷的原因。同时也可以看出,积云对流过程造成的对流加热Q1c占据了Q1的主要部分。同时也可以细心的发现,KF方案模拟的Q1c在对流层上部(200 hPa以上)为负的视热源,表现为降温作用,说明了KFeta方案模拟的对流层上部位温偏小主要是KF方案的对流加热调整造成的。

|
图 3 子时间段2的模拟和观测的时间平均垂直廓线(单位:K·d-1) (a)Q1,(b)Q1c,(c)Q2和(d)Q2c Fig. 3 Vertical profiles of time-averaged: (a) Q1, (b) Q1c, (c) Q2, and (d) Q2c over subcase 2 (unit: K·d-1) |
在子时间段2,不同方案模拟的Q2在700 hPa以上与观测值非常符合,但是在700 hPa下,则相差较大,不同方案模拟Q2都比观测值小,其中KFeta方案模拟的Q2比其他方案都弱。Q2小,说明减湿能力相对小,因此造成KFeta方案模拟对流底层相对湿润。比较图 3c和3d,可以发现Q2和Q2c差别还是比较大的,比如BMJ方案模拟的Q2c在对流层底层达到12 K·d-1,但是Q2则才3 K·d-1左右,这说明在对流层底层除了积云的减湿作用外,还有其他过程比如湍流过程对湿度产生重大影响。
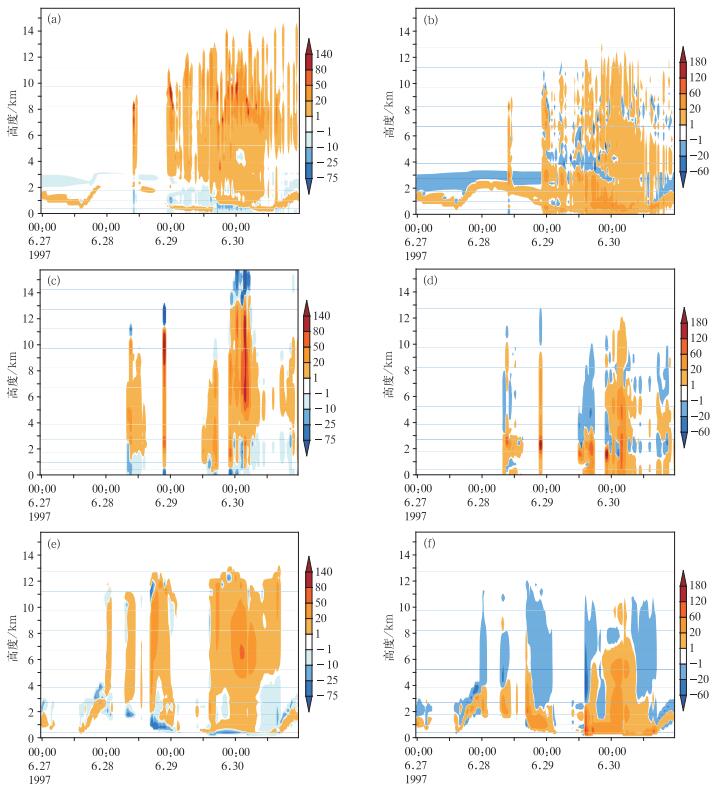
为了进一步考察不同积云参数化方案的性能,图 4给出了子时间段2不同方案向单柱模式反馈的温度倾向(即Q1c)和湿度倾向(即Q2c)的高度-时间图,为了方便比较和凸显积云作用,已经将温度倾向和湿度倾向的单位转化成K·d-1,分别表示了积云的加热效应和减湿效应,注意减湿效应正值表示湿度倾向为负,体现的是减湿作用,负值则相反。从该图中可以看出积云参数化方案的激发情况(激发强度和云顶高度等随时间的变化)。从图 4a,4c和4e可以看出,尽管不同方案都能很好地模拟出降水,但是不同方案的激发仍体现出很大的不同。从图 4a和4b中可以看出,SAS方案在6月27日00时到28日11时(UTC,下同)之间激发出浅对流,浅对流云顶高度在3 km左右,表现为浅对流上部冷却加湿,下部加热减湿,意味着在浅对流中,热量向下输送,水汽则向上输送。BMJ方案也在28日00时之前激发出浅对流,其效应与SAS方案类似,都表现热量向下输送,水汽向上输送。考虑到27日18时观测已经开始出现降水,在27日00时到28日00时之间模拟出浅对流有一定的合理性,而BMJ方案在28日00时就开始激发出深对流,则与观测更为相符。KFeta方案在28日08时之时才开始激发出深对流,之前并无激发对流,因此与其他方案相比,KFeta方案的浅对流激发频率偏低。从激发的深对流来看,与其他方案相比,KFeta方案激发频率仍偏低,但是模拟的深对流则更为强盛。加热效应的高度体现着积云参数化方案模拟的云顶高度。在子时间段2中,BMJ模拟的深对流云顶高度在13 km左右以下,SAS方案则相对高,可以达到14 km,KFeta方案模拟的云顶高度最高,可以到16 km左右,同时在KFeta方案中模拟强对流顶部,还存在着强烈的冷却作用。这是由于KFeta方案允许对流穿透,所谓的对流穿透,是指当云体的温度小于环境温度时,仍可以上升,直到云体垂直速度等于0,因此KFeta方案模拟的云顶较高。允许对流穿透,存在物理合理性,但是从产生的云高以及位温偏差来看,KFeta方案模拟的对流穿透无疑是过强的,这跟Liu等(2001)研究结果一致。
|
图 4 子时间段2 SAS(a, b)、KFeta(c, d)和BMJ(e, f)方案模拟的加热(a, c, e)和减湿(b, d, f)效应高度-时间图(单位:K·d-1) Fig. 4 The time-height SAS (a, b), KFeta (c, d) and BMJ (e, f) parameterized convective heating (a, c, e) and drying (b, d, f) effect (unit: K·d-1) over subcase 2 |
Liu等(2001)认为,KF方案造成低层偏湿的原因主要是KF方案缺少模拟浅对流和层积云的能力(KF方案不包含浅对流)。现KFeta方案虽引入浅对流方案,但前面分析表明其浅对流激发频率偏低。由于浅对流的作用是在低层向上输送水汽,因此浅对流方案的缺失或激发频率过低也是造成低层偏湿的一个因素。相对于其他两个方案,BMJ方案则偏向于在对流层上部产生较强的减湿效应负值(图 4f),造成对流层上部偏湿,对流低层则偏干。
4 KFeta方案的修改试验 4.1 KFeta方案的修改 4.1.1 KFeta修改方案1前面的研究表明,KFeta方案存在着因模拟的对流穿透过强导致对流层上部偏冷的问题。由于在KFeta方案中垂直速度方程控制对流穿透,因此可以考虑修改其垂直速度方程来解决这一问题。估算积云的垂直速度向来是个棘手的问题,一则缺少观测资料,对积云对流的垂直速度大小缺少认识,二则影响积云垂直速度的因素除了浮力外还有气压扰动、湍流动能增长和夹卷作用等(Gregory et al, 2001),这些因素估算也是让人头疼的问题。Simpson等(1969)提出积云对流的垂直速度方程可以写成
| $ \begin{array}{l} \frac{1}{2}\frac{{{\rm{d}}w_u^2}}{{{\rm{d}}z}} = \frac{g}{{\left({1 + \gamma } \right)}}\left({\frac{{{T_u} - \bar T}}{{\bar T}} - {\gamma _h}} \right) - \\ w_u^2\lambda - \beta {C_d}w_u^2\lambda \end{array} $ | (1) |
式中,wu为云的垂直速度,Tu为云的上升气流的虚温,T为环境虚温度,γh为云中所包含水凝物的混合比,g为重力加速度,γ=0.5,λ为环境空气卷入率,单位为m-1,β=1.875,Cd=0.5。其中方程右边第一项为浮力项,为了模拟湍流效应,将浮力项减为原来的(1+γ)-1,第二项为夹卷项,第三项是为体现气压扰动因素对垂直速度影响而引入的项。
KFeta方案中的垂直速度方程与式(1) 类似,但是缺少方程右边第三项。因此本研究对KFeta方案垂直速度的算法做了以下修改:(1) 引入表示气压扰动效应项,即加入式(1) 中右边第三项;(2) 在试验中发现,做了修改(1) 后,虽垂直速度有所减小,但是仍然穿透过强,因此参考欧洲中心的积云参数化方案(ECMWF:IFS document-Cy36r1) 中求对流上升气流垂直速度的算法,将浮力项削减为原来的(2+2γ)-1,即加强了湍流作用对垂直速度的影响;(3) 在KFeta方案中,λ与模式层之间的气压差成正比,因此,λ随高度倾向于减小,可以从云底的2×10-4 m-1到云顶附近减到0.5×10-4 m-1,使得在高层垂直速度的变化越来越依赖浮力项,进而加剧了积云对流穿透,为了克服这个缺点,在计算垂直速度时,将λ最小值设置为1.5×10-4 m-1;(4) 在KFeta方案中上升气流中水凝物在某一模式层内换成降水的多少与cdz/w成正比,其中dz模式层厚度,w为上升气流垂直速度,c为系数,其值一般为0.01~0.03 s-1,原方案设置为0.03 s-1,修改垂直速度方程后,KFeta方案模拟垂直速度减小,为了不致使模拟的降水偏高,将c系数设置成0.02 s-1。这种修改云的垂直速度后的方案简记为KFeta_w。
4.1.2 KFeta修改方案2Anderson等(2007)认为可以通过修改KFeta方案的流出层来减缓KFeta方案对流穿透过强的问题。在KFeta方案中,上升气流质量通量在流出层线性递减为零。Anderson等提出的修改如下:将流出层的底层设定在网格相当位温最小的层和融化层(ML)中比较低的层,并且在流出层中,上升气流质量通量随气压的自然对数线性递减而不是原来的随气压线性递减。Anderson的修改方案记为KFeta_flux。
4.2 修改的KFeta方案单廓线的检验把前面单柱模式积分过程中(子时间段2) 可以产生强对流的某一垂直廓线输出(图 5),用来简单诊断和讨论修改对KFeta方案的影响。
|
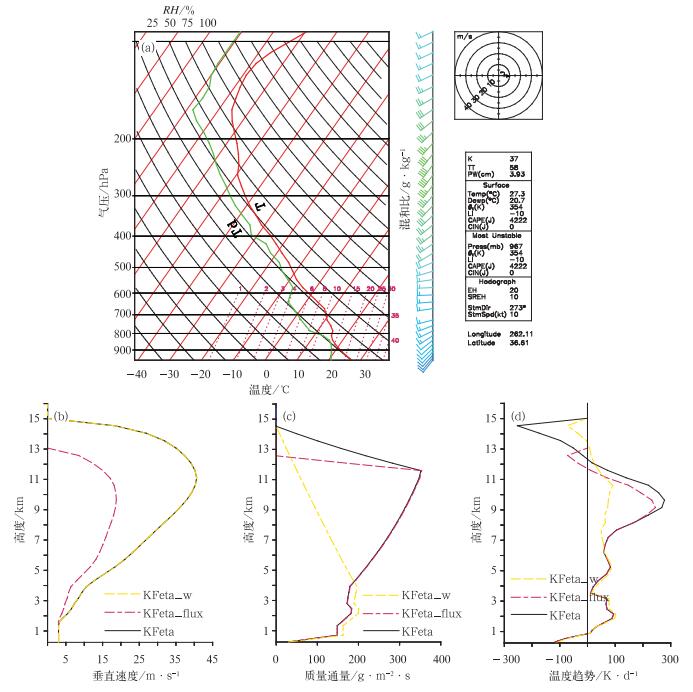
图 5 (a)可以产生强对流的温度(单位:℃)、露点温度(单位:℃)和风标(单位:m·s-1)的垂直廓线,(b)KFeta方案模拟的垂直速度(单位:m·s-1),(c)上升气流的质量通量(单位:g·m-2·s)和(d)对流加热廓线(单位:K·d-1) Fig. 5 (a) The profiles of temperature (unit:℃), dewpoint temperature (unit:℃) and wind barbs (unit:m·s-1) that can produce severe convection, (b) parameterized vertical velocity (unit:m·s-1), (c) parameterized updraft mass flux (unit:g·m-2·s), (d) parameterized convective heating profile (unit:K·d-1) |
从图 5a可以看出该廓线情形下,大气环境比较湿润,存在着非常大的对流不稳定能量。原KFeta方案模拟的云顶高度达到15 km,最大垂直速度达到40 m·s-1,位于11 km左右(图 5b),对应的加热廓线在9 km高度左右达到260 K·d-1,紧接着在14~15 km高度上出现强烈的冷却作用,达到-250 K·d-1左右(图 5d)。修改垂直速度方程后,其最大垂直速度减小到18.7 m·s-1,出现在10 km高度,相应其云顶高度大约在13.3 km高度,加热廓线在云顶附近的强烈冷却作用已经大为减小,最强的为-100 K·d-1。Anderson等修改显然对垂直速度和云顶高度没有影响,因其修改的是流出层,因此对上升气流的质量通量影响尤为明显(见图 5c),其模拟的上升质量通量在4 km左右就开始随高度线性递减,由于模拟的云上部质量通量变小,对应的卷出也变小,故使得积云对环境的影响减小,如图 5d所示,KFeta_flux试验模拟的加热廓线最大幅度小于100 K·d-1,冷却作用也在-60 K·d-1左右。
以上分析表明,本文提出的修改云的垂直速度的方案和Anderson提出的修改方案都对KFeta方案对流穿透过强的现象有了明显改进。
4.3 修改的KFeta方案在单柱模式中的检验为了进一步检验以上两种修改对KFeta方案的影响,下面将两种修改放到单柱模式中,重复前面模拟的试验,检验效果。
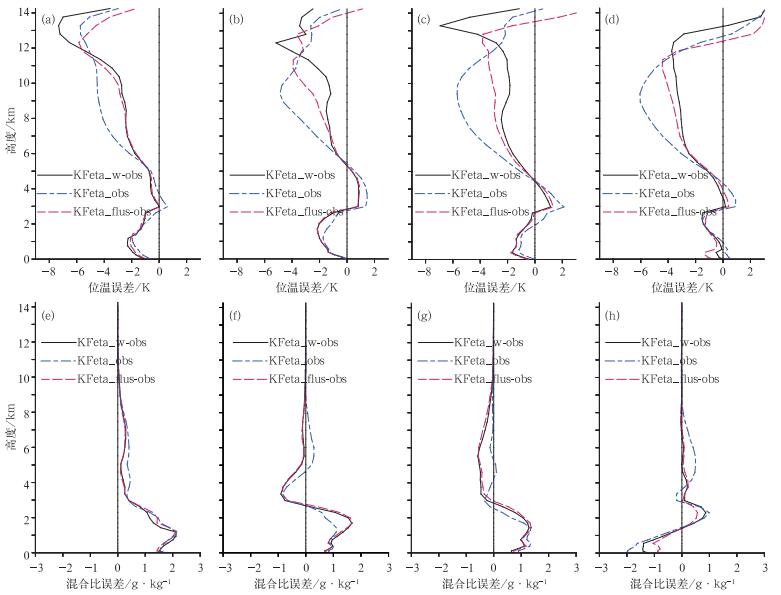
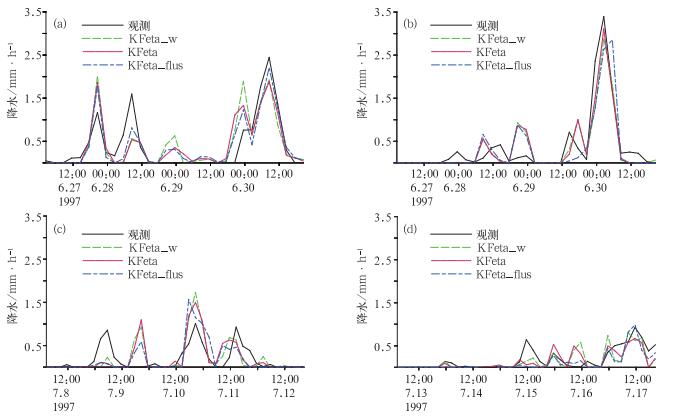
图 6给出了位温和水汽混合比平均误差的垂直廓线。可以看出,修改垂直速度方程后,能有效减少12~14 km处的位温误差,对湿度则影响不大。Anderson等的修改虽然可以减少12~14 km处的位温误差,但也同时加大了在7~12 km处的位温误差,这主要是由于该修改减小上升气流的质量通量,增加了卷出,从而减小了中上层加热效应,同理该修改也使得其模拟水汽混合比在7~12 km之间相对于原方案偏湿。从图 7及表 1可以看出,修改垂直速度后,对降水影响不大;Anderson修改模拟的降水在子时间段3和4较明显的减少。
|
图 6 不同修改方案子时间段1~4的时间平均位温误差(a~d, 单位:K)和水汽混合比误差(e~h, 单位:g·kg-1)的垂直廓线 Fig. 6 Same as Fig. 2, but for KFeta Scheme and its modified schemes |
|
图 7 不同修改方案对子时间段1~4的降水模拟(a~d,单位:mm·h-1) Fig. 7 Same as Fig. 1, but for KFeta and its modified schemes |
为了进一步考察上述两种修改对KFeta方案性能的影响,本文选取2007年7月7日00时(UTC,下同)至8日00时发生在安徽和江苏一带的梅雨暴雨过程作为实际个例使用GRAPES_meso模式进行模拟。采用NCEP 1°×1°的6 h一次的再分析资料为初始场和边界场,陆面方案采用Noah方案,边界层方案采用YSU方案,微物理方案采用WSM6方案,分辨率为0.15°,积分区域为10°~47.35°N、85°~137.35°E,起报时间为7日00时,积分24 h。相应的试验采用相应的积云参数化方案,其他模式配置完全一致。
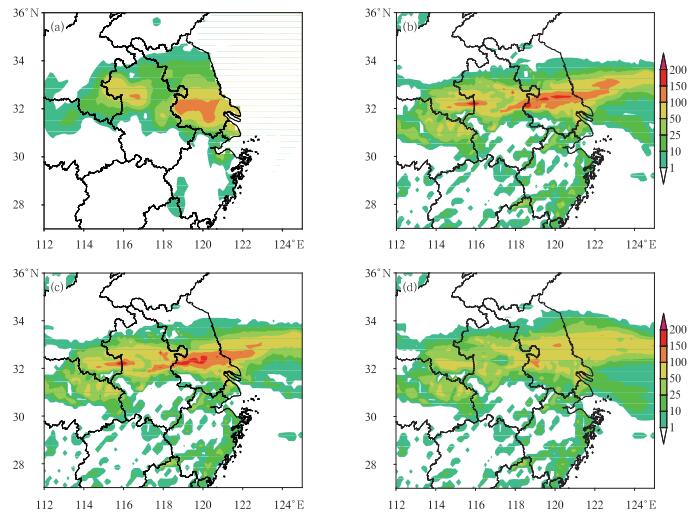
图 8给出了2007年7月8日00时的24 h累积降水分布。观测的降水资料为站点加密资料。可以看出,原方案很好地模拟了位于安徽和江苏地区梅雨暴雨过程,但是降水量偏大。KFeta_w试验对降水的分布影响不大,KFeta_flux试验则由于减小了方案中的上升气流质量通量,因此使模拟的暴雨中心降水有所减小,低于观测。
|
图 8 2007年7月8日00时24 h累积降水图(单位:mm) (a)观测,(b)KFeta,(c)KFeta_w和(d)KFeta_flux Fig. 8 The 24 h precipitation (unit: mm) at 00 UTC 8 June 2007 for (a) observation, (b) KFeta, (c) KFeta_w and (d) KFeta_flux |
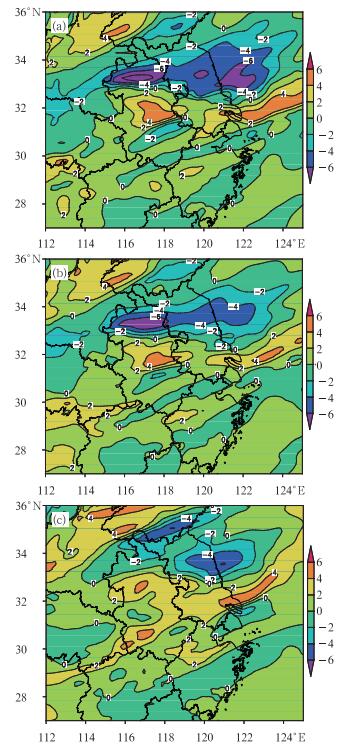
由于此处主要关注的是修正原方案在高层产生的负位温误差,因此图 9给出7月8日00时不同方案预报的100 hPa位温与FNL再分析资料的位温差异分布。从图 9可以看出,KFeta试验在安徽北部上空存在着-8 K的位温偏差,在江苏及东海上空存在着-6 K的位温偏差,两种修改都能有效地降低该处的位温偏差,冷误差的范围也有效的减小。
|
图 9 2007年7月8日00时不同方案模拟的100 hPa位温与NCEP FNL再分析资料位温差异(单位:K) (a)KFeta,(b)KFeta_w, (c)KFeta_flux Fig. 9 Potential temperature bias (unit:K) between simulated and NCEP FNL data at of 100 hPa at 00 UTC 8 June 2007 (a) KFeta, (b)KFeta_w and (c) KFeta_flux |
本文利用GRAPES单柱模式,采用GCSS WG4第三次个例模拟的观测数据,考察了积云参数化方案SAS、KFeta和BMJ方案对模拟的影响,并取得了一些有意义的结论。KFeta方案和BMJ方案都能较好地模拟出与实际相符的降水,但在模拟的温度和湿度上都体现出很大的不同。BMJ方案虽然在对流层中高层位温误差较小,但低层偏冷严重,同时,BMJ方案具有较强的水汽向上输送能力,易造成低层偏干,中高层偏湿,因此BMJ方案模拟的大气层结过于稳定。KFeta方案模拟的位温误差总的来说在低层相对于其他方案较小,在对流层高层则由于对流穿透过强导致偏冷严重,同时KFeta方案在低层有偏湿的倾向,这可能跟KFeta方案浅对流激发频率过低有关。SAS方案在子时间段1和2模拟出合理的降水,但在子时间段3和4则深对流激发不当,特别是子时间段4模拟的降水严重偏少,除大尺度强迫场的原因外,该试验模拟的低层偏干以及SAS方案激发机制较为严格是造成SAS深对流激发不足的重要原因。相应,SAS试验在子时间段3和4在6~11 km之间则偏冷严重,1.5 km高度以下则偏干。以上这些结果和结论为改进和研制积云参数化方案提供了参考。
本文针对KFeta方案穿透过强问题,提出了一种新的修改方案,即修改该方案中的垂直速度方程,添加表征气压扰动影响项,加强湍流作用,并对方程中的环境卷夹率设定下限,修改后的方案减小了模拟的垂直速度,减弱了穿透强度,从而减小了因穿透过强造成云顶偏冷的程度,通过单廓线试验、单柱模式试验和GRAPES_meso的一个实际个例试验表明修改后的方案能有效地改进对流层高层处的位温模拟。本文同时考察了Anderson等提出的修改,由于其修改是减小该方案中的上升气流质量通量,虽然能有效减少高层位温误差,但是易造成中高层偏冷,在实际模拟中也可能会造成降水量偏少的问题。综合来看,本文提出的修改方案的预报效果更令人满意。
本文只是对单柱模式试验简单的分析,并且将重点放在了KFeta方案中,对于BMJ和SAS方案体现出来的性质和问题则需要更深入分析,需要更多的个例模拟验证。研发适合东亚季风区的积云参数化方案是国内许多气象学者努力的方向(薛建军等,1999;许习华等,1999;左瑞亭等,2008)等,如能获取适合表征东亚地区对流系统的观测资料用于单柱模式检验积云参数化方案,这将为积云对流参数化方案的研究提供非常大的便利。
致谢:特别感谢杨军丽博士提供GRAPES单柱模式,并指导该模式的运行。特别感谢审稿专家提出的宝贵意见。
陈超君, 王东海, 李国平, 等, 2012. 冬季高海拔复杂地形下GRAPES_Meso要素预报的检验评估[J]. 气象, 38(6): 657-668. DOI:10.7519/j.issn.1000-0526.2012.06.003 |
陈德辉, 薛纪善, 杨学胜, 等, 2008. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究[J]. 科学通报, 53(20): 2396-2407. DOI:10.3321/j.issn:0023-074X.2008.20.002 |
纪永明, 陈静, 矫梅燕, 等, 2011. 基于多中心TIGGE资料的区域GRAPES集合预报初步试验[J]. 气象, 37(4): 392-402. DOI:10.7519/j.issn.1000-0526.2011.04.002 |
王建捷, 胡欣, 郭肖容, 2001. MM5模式中不同对流参数化方案的对比试验[J]. 应用气象学报, 12(1): 41-53. |
熊秋芬, 2011. GRAPES_Meso模式的降水格点检验和站点检验分析[J]. 气象, 37(2): 185-193. DOI:10.7519/j.issn.1000-0526.2011.02.008 |
徐国强, 陈德辉, 薛纪善, 等, 2008. GRAPES物理过程的优化试验及程序结构设计[J]. 科学通报, 53(20): 2328-2434. |
徐国强, 黄丽萍, 薛纪善, 等, 2005. 中国冬夏季模式降水方案的应用分析研究[J]. 气象学报, 63(1): 49-56. DOI:10.11676/qxxb2005.006 |
许习华, 丁一汇, 1999. 一种考虑云相互作用的积云对流参数化方案及其在降水预报中的应用[J]. 中国科学(B辑), 9: 998-1008. |
薛建军, 闫之辉, 1999. 一种改进的质量通量积云参数化方案及其预报试验[J]. 气象, 25(5): 8-11. DOI:10.7519/j.issn.1000-0526.1999.05.002 |
杨军丽, 沈学顺, 2012. GRAPES单柱模式的试验研究[J]. 气象学报, 70(2): 275-290. DOI:10.11676/qxxb2012.027 |
左瑞亭, 王丽琼, 钱贞成, 等, 2008. 当前对流参数化研究存在问题的讨论[J]. 热带气象学报, 24(6): 732-736. |
Anderson C J, Arritt R W, Kain J S, 2007. An alternative mass flux profile in the Kain-Fritsch convective parameterization and its effects in seasonal precipitation[J]. J Hydrometeor, 8: 1128-1140. DOI:10.1175/JHM624.1 |
Arakawa A, Schubert W H, 1974. Interaction of a cumulus cloud ensemble with the large-scale environment, Part Ⅰ[J]. J Atmos Sci, 31: 674-701. DOI:10.1175/1520-0469(1974)031<0674:IOACCE>2.0.CO;2 |
Betts A K, 1986. A new convective adjustment scheme. Part Ⅰ: Observation and theoretical basis[J]. Quart J Roy Meteor Soc, 112: 677-691. |
Betts A K, Miller M J, 1986. A new convective adjustment scheme. Part Ⅱ: single column test using GATE wave, BOMEX, ATEX and arctic air-mass data sets[J]. Quart J R Met Soc, 112: 693-709. |
Cederwall R T, Rodriques D J, Krueger S K, et al.1999.The ARM-GCSS intercomparison study of single-column models and cloud system models. 9th Atmospheric Radiation Measurement Science Team Meeting, San Antonio, TX(US). http://digital.library.unt.edu/ark:/67531/metadc735448/
|
Davis C, Bosart L F, 2002. Numerical simulations of the Genesis of Hurricane Diana (1984). Part Ⅱ: Sensitivity of track and intensity prediction[J]. Mon Wea Rev, 130: 1100-1124. DOI:10.1175/1520-0493(2002)130<1100:NSOTGO>2.0.CO;2 |
Deshpande M, Pattnaik S, Salvekar P S, 2010. Impact of physical parameterization schemes on numerical simulation of supper cyclone Gonu[J]. Nat Hazards, 55: 211-231. DOI:10.1007/s11069-010-9521-x |
ECWMF. IFS documentation-Cy36r1. Part Ⅳ: Physical processes. http://193.63.95.1/research/ifsdocs/CY36r1/PHYSICS/IFSPart4.pdf.
|
Gregory D, 2001. Estimation of entrainment rate in simple models of convective clouds[J]. Quart J R Met Soc, 127: 53-72. DOI:10.1002/(ISSN)1477-870X |
Grell G A, 1993. Prognostic evaluation of assumptions used by cumulus parameterizations[J]. Mon Wea Rev, 121: 764-787. DOI:10.1175/1520-0493(1993)121<0764:PEOAUB>2.0.CO;2 |
Janjic Z I, 1994. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer and turbulence closure schemes[J]. Mon Wea Rev, 122(5): 927-945. DOI:10.1175/1520-0493(1994)122<0927:TSMECM>2.0.CO;2 |
Kain J S, 2004. The Kain-Fritsch convective parameterization: An update[J]. J Appl Meteor, 43: 140-181. |
Kain J S, Fritsch J M, 1990. A one-dimensional entraining/detraining plume model and its application in convective parameterization[J]. J Atmos Sci, 47(23): 2784-2802. DOI:10.1175/1520-0469(1990)047<2784:AODEPM>2.0.CO;2 |
Krueger S K, Cederwall R T, Xie S C, et al, 1999. GCSS WORKing Group 4 model intercomparison, procedures for Case 3:summer 1997 ARM SCM IOP[J]. Technical report. |
Li Xuanli, Pu Zhaoxia, 2009. Sensitivity of numerical simulations of the early rapid intensification of Hurricane Emily to cumulus parameterization schemes in different model horizontal resolutions[J]. J Meteor Soc Japan, 87(3): 403-421. DOI:10.2151/jmsj.87.403 |
Liu C H, Moncrieff M W, Grabowski W W, 2001. Explicit and parameterized realizations of convective cloud systems in TOGA COARE[J]. Mon Wea Rev, 129: 1689-1703. DOI:10.1175/1520-0493(2001)129<1689:EAPROC>2.0.CO;2 |
Ramanathan Y, 1980. Cumulus parameterization in a case study of a monsoon depression[J]. Mon Wea Rev, 108(3): 313-321. DOI:10.1175/1520-0493(1980)108<0313:CPIACS>2.0.CO;2 |
Lord S J, 1982. Interaction of a cumulus cloud ensemble with the large-scale environment. Part Ⅲ:semi-prognostic test of the Arakawa-Schubert cumulus parameterization[J]. J Atmos Sci, 39: 88-103. DOI:10.1175/1520-0469(1982)039<0088:IOACCE>2.0.CO;2 |
Simpson J, Wiggert V, 1969. Models of precipitating cumulus towers[J]. Mon Wea Rev, 97: 471-489. DOI:10.1175/1520-0493(1969)097<0471:MOPCT>2.3.CO;2 |
Xie Shaocheng, Xu Kuan-Man, Cederwall R T, et al, 2002. Intercomparison and evaluation of cumulus parametrizations under summertime midlatitude continental conditions[J]. Quart J R Met Soc, 128: 1095-1135. DOI:10.1256/003590002320373229 |
 2013, Vol. 39
2013, Vol. 39 
