“山洪”是指山区中小流域河谷地带发生的暴涨洪水,一般情况下山洪多为暴雨所致,有发生突然、水量集中、流速大等特点,极具冲刷破坏力(刘志雨等,2010)。山洪及其诱发的次生灾害,常造成人员伤亡、房屋毁坏、田地淹没、道路桥梁冲垮等灾害,对国民经济和人民生命安全造成严重危害。近年来山洪灾害越发严重,已引起各级政府的高度重视,故迫切需要山洪灾害的有效预警方法来为政府提供服务。
目前山洪灾害预警公认的依据指标为风险临界雨量(江锦红等,2010),即一定时段内降水量达到或超过一定临界雨量时,立刻启动防洪减灾预案。目前有关临界雨量的计算方法主要有实测雨量分析法、降雨灾害频率分析法、产汇流对比分析法及暴雨临界曲线法(江锦红等,2010;段荣生,2009;刘哲等,2005;郑永山,2010),应用这些方法可以计算得出洪灾发生时的临界雨量。对于无水文观测资料的山区流域,前人的研究多采用类比法(郑永山,2010),但由于山洪流域的局地性和特殊性,很难找到相似的流域进行替代,因此该方法的可行性也不强。
为了更好地计算无水文资料的山区流域的致灾临界雨量,本文引进了德国研发的洪水动态淹没模型“Floodarea”(Geomer,2003),在基于实地调查的基础上,针对无水文资料、无长序列气象观测资料,但有洪水淹没个例的流域,进行山洪风险雨量的计算。
1 方法简介 1.1 “Floodarea”计算原理“Floodarea”为德国Geomer公司开发的洪水淹没模型,该模型内嵌于Arcgis平台,计算基于水动力方法,同时考虑了一个栅格的周围8个单元(图 1)。对邻近栅格单元的泻入量由manning-stricker公式计算(Geomer,2003)。坡度由单元之间的最低的水位和最高的地形高程之间的差异所决定,对每一个单元都进行计算。相邻单元的流量长度被认为是相等的;位于对角线的单元,以不同的长度算法来计算。不同于静态洪水风险区划图,“Floodarea”在每个时相的运行过程,即运行时间与相应淹没范围和水深,都以栅格形式呈现和存储,直观明了,易于查询(苏布达等,2005)。
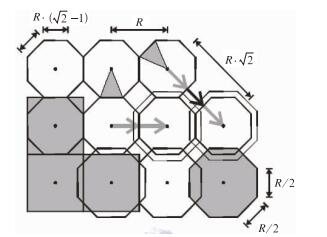
|
图 1 栅格单元划分图 Fig. 1 Grid cell division |
水流的淹没深度为淹没水位高程和地面高程之间差值,由式(1) 表示(Geomer,2003):
| $ flow\_depth = water\_leve{l_a} - elevatio{n_a} $ | (1) |
淹没过程中的水流方向由地形坡向所决定,地形坡向反映了斜坡所面对的方向,坡向指地表面上一点的切平面的法线矢量在水平面的投影与过该点的正北方向的夹角。对地面任何一点来说,坡向表征了该点高程值改变量的最大变化方向。计算公式由式(2) 表示(Geomer,2003):
| $ aspect = 270 - \frac{{180}}{\pi }\alpha \tan 2\left( {\frac{{\partial Z}}{{\partial Y}} + \frac{{\partial Z}}{{\partial X}}} \right) $ | (2) |
其中,α为地形坡度。
1.2 “风险雨量”计算方法山区中小流域中发生不同等级的洪水淹没时所对应的某时段的降水量即为该淹没等级的风险雨量,风险雨量分为高、中、低三个等级,一般用1 h或几个小时的降雨量(单位:mm)表示(江锦红等,2010)。
对于无水文资料的山区流域进行实地考察,选择山洪隐患点,调查往年洪水淹没的深度,以人口集中、经济发达的区域作为山洪预警点。根据数字高程模型(digital elevation model, DEM)、地表产流系数、地表水力糙度、及以往山洪发生时的降水资料,利用“Floodarea”模型进行山洪淹没再现模拟,根据预警点的调查资料对模拟结果进行调整。提取最佳模拟结果中预警点逐时的淹没深度,对逐时淹没深度及对应降水量进行分析,最终得出不同风险等级的临界面雨量。
2 实例分析 2.1 山洪流域基本情况上清溪流域位于福建省三明市泰宁县境内,是一个无水文资料的典型山区小流域,流域境内有包括乡政府驻地在内的数十个行政、自然村,上清溪呈西北—东南走向,境内地势海拔为332~1256 m,流域面积仅为76 km2,为典型的高山峡谷型河流流域,大部分区域地表产流系数相对较大,一场暴雨过程极易形成产流,狭小的地形连锁引发山洪。由于流域地势陡峭,河谷狭小,且处于大山深处,无水文观测资料,目前只有气象局的4个气象观测自动站近几年的观测资料。
2010年6月上清溪遭遇了连续长时间的暴雨袭击,伴有突发短历时强降水事件,据自动气象站观测记录显示,6月18日11时单站最大小时雨量竟达85.2 mm,上清乡遭遇了超百年一遇的特大洪涝灾害。
2.2 资料计算所用地理信息资料(1:10000) 及遥感资料(1:50000) 来自福建省地理信息院,降水资料来自福建省气象局;通过实地考察获得灾情淹没记录。
2.2.1 实地考察选择流域内的8个村落作为风险隐患点(表 1和图 2)考察对象,针对2010年6月18日的山洪灾害进行考察,考察内容有受灾点洪水淹没深度及时间、河道宽度、堤坝高度及人口分布。
|
|
表 1 上清溪洪水隐患点实地考察表 Table 1 Form of investigation in Shangqing River valley |
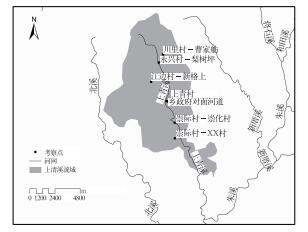
|
图 2 上青流域考察点分布图 Fig. 2 Distribution of investigated spots in Shangqing River Valley |
根据实地考察得知,上青乡政府驻地位于上清溪流域的中部,该地人口集中、经济相对发达,故选择上青乡政府驻地作为上清溪流域山洪淹没预警点。
2.2.3 流域面雨量根据DEM数据,利用ArcGIS软件计算得出上清溪流域范围,再根据流域范围内及周围的气象自动站点,利用ArcGIS制作流域所在区域的泰森多边形, 最后采用权重法计算得出流域的面雨量,计算方法如下:
| $ {A_{\rm{R}}} = \sum\limits_{i = 1}^n {{R_i} \times {A_i}/A} $ | (3) |
式中,AR为流域面雨量,Ri为站点i的雨量,Ai为站点i代表的泰森多边形面积,A为流域总面积,n为泰森多边形个数。
2.2.4 地表水力糙度水力糙度指的是流体力学上的粗糙度,是衡量河道或冲沟边壁形状不规则性和粗糙程度影响的一个综合性系数,目前关于水力糙度的研究较多(童星等,2011)。利用遥感资料对流域内地面覆盖类型,根据张洪江等(1994)的研究结论对流域内不同地面覆盖类型的水力糙度赋初值,本文对流域地表水力糙度取值介于1~10之间。根据洪水再现淹没模拟效果对水力糙度进行率定,以调节洪水淹没过程中水流的速度,上清溪流域地表水力糙度率定结果如图 3所示。
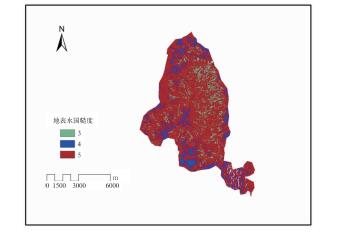
|
图 3 上青流域地表水力糙度 Fig. 3 Water roughness value of surface hydraulic power in Shangqing River Valley |
SCS(Soil Conservation Service)模型应用于无资料地区径流模拟,依据地表覆盖类型来确定SCS模型的参数(甘衍军等,2010)。模型能够客观反映土壤类型、土地利用方式及前期土壤含水量对降雨径流的影响,其显著特点是模型结构简单、所需输入参数少,是一种较好的小型集水区径流计算方法(刘家福等,2010)。SCS模型计算公式如下:
| $ S = \frac{{25400}}{{CN}} - 254 $ | (4) |
| $ Q = \frac{{{{\left( {P - 0.2S} \right)}^2}}}{{P + 0.8S}} $ | (5) |
| $ k = \frac{Q}{P} $ | (6) |
式中,Q为产流量,P为当天降水量,k为产流系数;S为潜在入渗量,CN反映流域前期土壤湿润程度、坡度、土壤类型和土地利用现状的综合特性, 可以较好地反映下垫面条件对产汇流过程的影响,CN值由地表覆盖类型确定,可查表获得(Mockns et al,1985)。
根据地面覆盖类型,通过式(4)~式(6) 计算得出上清溪流域地表产流系数,根据受灾隐患点位置洪水再现淹没模拟效果对参数进行率定,以调节洪水淹没过程中洪水淹没深度,上清溪流域地表产流系数率定结果如图 4所示。
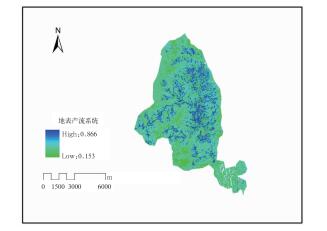
|
图 4 上青流域地表产流系数 Fig. 4 Runoff coefficient value in Shangqing River Valley |
根据上清溪流域地面水力糙度、地表产流系数和2010年6月18日暴雨过程面雨量,利用“Floodarea”淹没模型对2010年6月18日暴雨过程造成的淹没状况进行再现模拟。模拟结果见图 5,由图可见,随着时间的推移,洪水向中、下游堆聚,集中在上清至崇际村—从化村一带,下游水深增加,最后流域水位全部上涨,范围扩大至上游,与实际考察过程吻合。
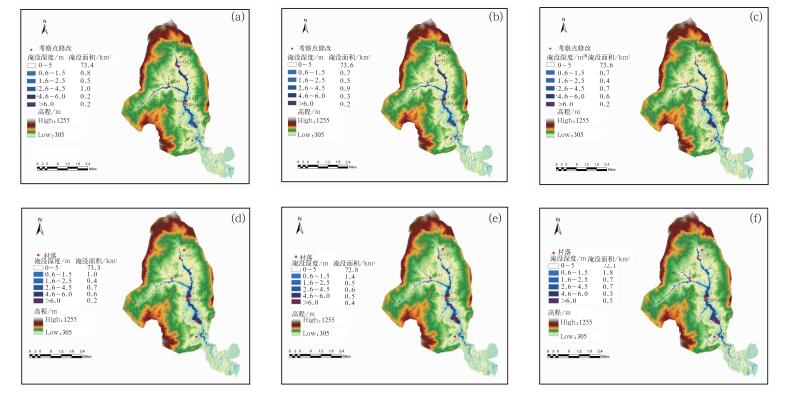
|
图 5 上清溪流域2010年6月18日洪水淹没过程模拟 (a)06:00, (b)07:00, (c)08:00, (d)09:00, (e)10:00, (f)11:00 Fig. 5 Simulation of the flood on 18 June 2010 in Shangqing River Valley (a) 06:00, (b) 07:00, (c) 08:00, (d) 09:00, (e) 10:00, (f) 11:00 |
上清溪流域2010年6月18日洪水淹没过程模拟,预警点各时段淹没深度如表 2所示。由表 2可以看出,雨量较小且降水时间短时预警点淹没水深基本为地表产流造成,随着降水量的增加和降水强度的增强,淹没水深会突然增大。对比实地考察资料,预警点考察淹没水深最高为1.14 m,模拟淹没水深最高为1.411 m,模拟结果高稍高于调查结果,但二者最高水深的淹没时间相一致,均为上午09时左右。
|
|
表 2 预警点洪水淹没水深及对应面雨量 Table 2 Flood depth and corresponding precipitation at the warning spots |
根据上清溪流域2010年6月18日洪水淹没过程模拟结果及实地考察资料,利用隐患点水位及其对应的各小时累计面雨量建立相关方程;由于淹没模型模拟过程中,最高淹没高度比实际淹没高度偏高约0.27 m,因此,在利用拟合方程推算隐患点处时,基于河坝坝高的淹没水深对应的不同累计小时雨量时,将水位增加0.27 m;推算结果见表 3。由表可见,超过4 h累计面雨量趋于稳定,故选择4 h累计面雨量作为上清溪流域致灾临界雨量。
|
|
表 3 预警点不同等级的风险雨量 Table 3 Risk precipitation in different grades at warning spots |
(1) “Floodarea”淹没模型能够为无水文资料的山区小流域的风险临界雨量研究及洪水淹没灾害评估提供较好的技术支撑。
(2) 短历时强降水为山区小流域洪水淹没的主要致灾因子,长时间的低强度降水对山洪爆发形成的潜在诱因也不容忽视。
3.2 不足(1) 山区雨量观测站少,导致暴雨过程中山区小流域逐时面雨量计算结果的准确度偏低。
(2) 山区小流域有淹没记录的暴雨山洪样本少,导致流域风险雨量计算结果的准确度偏低。
段荣生, 2009. 典型小流域山洪灾害临界雨量计算分析[J]. 水利规划与设计, (2): 20-21, 57. |
甘衍军, 李兰, 杨梦斐, 2010. SCS模型在无资料地区产流计算中的应用[J]. 人民黄河, 32(5): 30-31. |
江锦红, 邵利萍, 2010. 基于降雨观测资料的山洪预警标准[J]. 水利学报, 41(4): 458-463. |
刘家福, 蒋卫国, 占文凤, 2010. SCS模型及其研究进展[J]. 水土保持研究, 17(2): 120-124. |
刘哲, 张鹏远, 刘广成, 2005. 黑龙江省山洪灾害防治临界雨量计算分析[J]. 黑龙江水利科技, 33(5): 10. |
刘志雨, 杨大文, 胡建伟, 2010. 基于动态临界雨量的中小河流山洪预警方法及其应用[J]. 北京师范大学学报, 46(3): 317-321. |
苏布达, 姜彤, 郭业友, 等, 2005. 基于GIS栅格数据的洪水风险动态模拟模型及应用[J]. 河海大学学报, 33(4): 370-374. |
童星, 裴毅, 2011. 地表糙度与水力糙率间关系的试验研究[J]. 湖南农机, 38(3): 35-37. |
张洪江, 北原耀, 解明曙, 1994. 晋西几种不同土地利用状况下糙率系数的研究[J]. 北京林业大学学报, 16(supp.4): 86-91. |
郑永山, 2010. 甘肃省山洪灾害临界雨量分析[J]. 甘肃水利水电技术, 46(3): 5-6. |
Geomer.2003.Floodarea—Arcview extension for calculating flooded areas (User manual Version 2.4).Heidelberg.
|
Mockns V, Woodward D E.1985.National Engineering Handbook.Washington: Natural Resources Conservation Service.
|
 2013, Vol. 39
2013, Vol. 39 