引言

随着全球气候变化的加剧，以及城市化过程引发的诸多问题，城市大气环境问题已成为全球关注的热点问题之一。工业生产中矿物燃料燃烧、交通工具废气排放及冬季燃煤取暖等, 使城市大气环境不断恶化，不仅危害到人们的正常生活，而且威胁着人们的身心健康。污染物排放量和大气对污染物的稀释扩散能力是影响城市大气环境质量的两个主要因子。在污染物排放量一定的情况下, 污染浓度的日变化或月变化主要是由某些天气过程和天气系统影响城市边界层大气对污染物的稀释扩散能力造成的。大量研究发现城市大气污染与天气形势关系密切(Lam et al, 1998；Oanh et al, 2005；Bei et al, 2013；孟燕军等，2002)，不利于大气扩散的天气形势甚至造成严重的城市大气污染事件，如著名的伦敦烟雾事件和洛杉矶光化学烟雾事件就是大量污染物排放和不利天气形势共同作用的结果。Chen等(2008)通过分析天气形势对中国北方城市大气环境的影响，指出在高压及随后持续低压的天气形势下，空气污染指数(Air Pollution Index, API)会增加，冷锋前API达到极大值，冷锋过境时气压梯度增大，API迅速减小，大气污染物浓度降低。气象条件对不同污染成因造成的大气环境问题的影响也不同。对于区域性污染，如沙尘污染，风速增加虽然可使城市大气通风能力增强，但由于污染物(沙尘)输入的增加，大气污染可能加重；对于局地污染，风速增加使大气通风能力增强，大气污染减轻(Pasch et al, 2011)。区域天气形势和局地气象条件对大气污染的影响程度也不同，在一些地区局地气象条件对大气环境可能有决定性影响(Xu et al, 2011)。Pearce等(2011a；2011b)分析了墨尔本大气环境与天气形势和局地气象条件之间的关系，发现局地气象条件对大气环境的影响更大。Lu等(2012)模拟研究了气象条件对由南加州自然火灾所引起烟雾的输送和扩散的影响，发现复杂地形地区局地大气环流对大气污染物输送有很大的影响。李喜仓等(2011)分析了城市发展对大气环境的影响，发现城市发展影响局地环流，大气扩散能力减弱。

兰州属大陆性干旱半干旱地区，年降水量327.7 mm，其中50%的降水集中在7—10月，年平均气温9.3℃，年平均风速0.8 m·s^-1，年平均静风频率达62%，近地面盛行偏东风(Wang et al, 2009)。目前兰州市城区人口超过300万，大量工业生产排放、机动车尾气排放和燃煤取暖排放加上特殊的山谷地形影响，使兰州成为全国大气污染最严重的城市之一(张远航等，1987)，特别是冬季, 污染十分严重, 空气质量超标率达50%以上(陈雷华等，2010)。许多学者针对兰州市冬季大气污染成因做了大量有意义的工作。胡隐樵等(1999)定性分析了兰州大气污染的成因，指出冬季兰州山谷大气边界层长时间日夜维持的大气逆温和几乎静风的气象条件是造成兰州大气污染严重的客观原因，并提出了相应的治理对策；张强(2001)用Froude数分析了地形和逆温对兰州大气污染的影响，指出兰州山谷气流的Froude数远小于1，在一般的天气条件下, 地面污染物较难通过沿坡爬升方式输送出去；An等(2007)认为大气环境容量小造成了兰州市严重的大气污染，污染物排放量减少20%空气质量才能达到Ⅱ级标准；姜大膀等(2001)、王世功等(2000)和尚可正等(2001)利用短期实验观测资料、多年常规地面和探空观测资料分析了低空风和大气温度层结状况以及天气形势与城市空气污染的关系，指出低空风速、逆温层厚度和强度、日最大混合层厚度及稳定能量是影响兰州市空气质量的重要因素。

随着人们对城市大气环境问题的日益重视, 特别是2012年6月中华人民共和国环境保护部正式发布《重点区域大气污染防治“十二五”规划》，首次将民众最关心的细颗粒物(PM_2.5)纳入指标体系，对今后大气污染防治工作和保护人民群众身体健康等都具有十分重要的意义。同时，也对大气污染预报工作提出了更高的要求。本文利用WRF模式模拟高时空分辨率的优势, 通过模拟2011年11月1日至2012年2月29日兰州市区及其周边气象场，结合兰州市环境监测站的空气污染物浓度监测资料, 采用相关分析方法，分析兰州市冬季大气污染物浓度与气象因子的关系，明确主要影响因子以及影响因子与大气污染物浓度的关系，并建立预报模型，为开展城市空气质量预报提供参考。

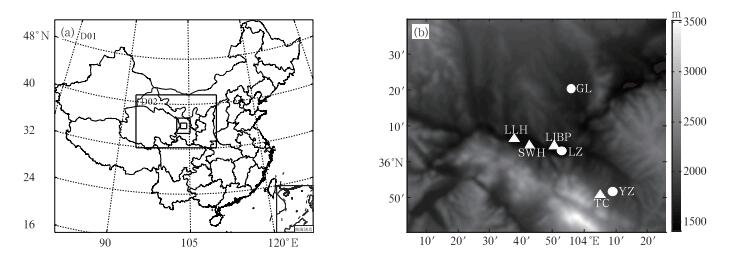
1 资料和研究方法 1.1 资料及来源

本文所用资料包括2011年11月1日至2012年2月29日兰州市4个大气环境监测点[职工医院(SWH)，生物制品研究所(LIBP)，兰炼宾馆(LLH)和三角城(TC)]的NO₂和PM₁₀小时平均浓度自动监测数据；研究区3个自动气象站点[兰州(LZ)、皋兰(GL)和榆中(YZ)每日8次(02、05、08、11、14、17、19和21时，LST)]地面常规观测资料和榆中(YZ)站08和20时的探空资料以及WRF模式模拟的研究区气象场。4个大气环境监测站和3个自动气象站的位置示于图 1b，其中LIBP、LLH和SWH 3个监测点位于兰州城区，TC监测点位于距离兰州城区48 km以外的榆中县城。城区监测点周边土地利用差异很大：SWH周边是小工厂和耕地，LIBP周边是居民区，LLH周边是工业区。为了尽量减少除气象条件以外的其他因素对大气污染物浓度的影响，选择兰州气温低、降水少和污染源相对稳定的冬季，并且在分析气象参数与污染物浓度之间的相关性时剔除了有降水的时段。另外，为了去除污染源排放量日变化的影响，分析中使用污染物浓度的日均值。

1.2 研究方法

目前，空气质量预报模式大致分为3类。第一类是无化学反应的预报模式，它主要由扩散模式和统计模式组成；第二类是考虑气象场的影响又考虑污染物化学反应的化学预报模式；第三类是空气质量信息系统，它是将与空气质量有关的资料系统、预报模式、预报系统、决策系统和评估系统等有机的结合在一起。我国空气质量预报主要方法有数值模式、数理统计和综合经验3类方法(朱玉强，2004)。姚琳等(2012)对成都市空气质量预报中WRF的本地化参数选取进行了研究；顾莹(2010)尝试利用WRF模拟结果作为观测值代入动力-统计预报模式进行预报，分等级预报的结果较为理想。本文使用WRF模式模拟研究区气象场, 通过分析兰州市冬季大气污染物浓度与气象因子的关系建立预报模型。

1.2.1 数值模拟方案

WRF模式系统是美国国家大气科学研究中心(National Center for Atmospheric Research，NCAR)、国家海洋和大气管理局(National Oceanic and Atmospheric Administration，NOAA)等多个部门联合开发的新一代高分辨率中尺度预报模式和资料同化系统, 分为ARW和NMM两个动力核。WRF-ARW是可压缩、欧拉、非静力平衡模式，控制方程组为通量形式，采用地形跟随静压垂直坐标系，水平网格采用Arakawa-C交错格式，模式顶层气压为常数。本研究采用WRF-ARW V3.3模式。

模拟试验微物理参数化选用WRF Single-Moment 6-class(WSM6) 方案(Hong et al, 2006)，积云参数化选用K-F方案(Kain, 2004)，辐射参数化选用长波辐射方案Rapid Radiative Transfer Model(RRTM)(Mlawer et al，1997)和Dudhia短波辐射方案(Dudhia, 1989)，边界层参数化选用YSU方案(Hong et al, 2006b)，近地面参数化选用Monin-Obukhov相似理论方案，陆面过程参数化选用包含城市参数化的Noah陆面过程模式(Chen et al, 1996)。

模式采用分段积分，将模拟时段(2011年10月30日至2012年2月29日)分为9段分别进行模拟，每段前24 h作为模式起转时间，不作分析。模式垂直方向分为35层，模式层顶气压为50 hPa。模式采用单向四重嵌套，网格距分别为27、9、3和1 km，第四重模拟区域覆盖了兰州市区及南北两山大部地区(图 1a)。模式初始场和侧边界条件由NCEP FNL资料(时间间隔6 h，空间分辨率1°×1°)提供。

1.2.2 影响因素的选取

影响边界层大气对污染物稀释扩散能力的因素主要有风、大气层结稳定度、混合层高度、逆温层厚度和强度等。风对大气污染物的稀释扩散和三维输送起着重要作用，是与空气污染密切相关的气象参数。在兰州特殊地形影响下, 低层风一般比较小，这与低层大气层结过于稳定使上层动量下传受阻有关。因此, 稳定的大气层结被认为是引起兰州空气重污染的因素之一(尚可政等，2001)。在以往的研究和应用中理查森数被用来描述低层大气的稳定度, 逆温厚度和强度被用来描述近地面层的逆温状况, Froude数被用来衡量山谷地形下稳定大气边界层的气流越山能力(张强，2001)，输送指数或通风指数被用来描述低层大气的扩散能力(Termonia et al, 2004)，大气边界层总体稳定度参数被用来衡量大气边界层湍流运动能力。

根据研究区的特点，选取风速、稳定能量、Froude数、边界层高度、位温递减率、输送指数和梯度理查森数来分析局地气象条件对兰州大气环境的影响。由于逆温强度和厚度无法描述没有逆温状态时大气的扩散能力，故采用反映大气层结状态的位温递减率取代。有研究指出兰州低空气象参数中稳定能量与污染物浓度之间相关性最显著，各月污染物浓度与稳定能量相关性最好的高度层位于500~850 m(尚可政等，2001)，因此计算了地面到500 m低空稳定能量。所选气象参数具体算法详见附录。

1.2.3 相关分析

本文用相关系数描述变量间的相关程度。常用的相关系数有Pearson积矩相关系数、Spearman秩相关系数和Kendall秩相关系数。用Kolmogorov-Smirnov法，取显著性水平为0.05，检验变量是否服从正态分布，结果表明日平均污染物浓度、风速、Froude数和输送指数服从对数正态分布，位温递减率、稳定能量和边界层高度服从正态分布，梯度理查森数是非正态分布。因此，用Pearson积矩相关系数描述风速对数、Froude数对数、输送指数对数、位温递减率、稳定能量和边界层高度与污染物浓度对数的相关性；用Spearman秩相关系数描述梯度理查森数与污染物浓度对数的相关性。下文将Pearson积矩相关系数和Spearman秩相关系数均简称为相关系数。

2 模拟结果检验及回归方程效果分析 2.1 气象场模拟结果检验

本节用命中率(HR)、平均偏差(MB)、均方根误差(RMSE)和标准差(SD)来评估WRF模式在研究区域的模拟能力。HR考虑了观测的不确定性，其结果可以反映模式的总体模拟性能，其值与所选控制值大小有关。气温、相对湿度和风速的控制值分别取2℃、10%和1 m·s^-1(Papalexiou et al, 2006；Miao et al, 2009)。

表 1给出了第四重模式区域模拟结果与3个自动气象站和1个探空站观测值对比统计结果。WRF模式模拟的气温比观测值偏高，模拟的近地面气温标准差较观测标准差小。WRF模式对上层气温的模拟效果好于近地面气温，近地面相对湿度和风速模拟效果较上层好。WRF模式在不同研究区的模拟能力不同，Miao等(2009)利用WRF模式模拟研究了北京地区城市热岛和边界层结构的变化，得到WRF模拟的2 m气温、2 m比湿和10 m风速的HR分别是70%、60%和62%，MB分别是0.2℃、-1.61 g·kg^-1和0.3 m·s^-1，RMSE分别是1.94℃、2.19 g·kg^-1和1.1 m·s^-1。尽管兰州地区地形复杂，统计评估结果与其他地区基本相当，WRF模式能很好地模拟兰州地区气象场。

2.2 日平均污染物浓度与气象影响因素的相关性分析

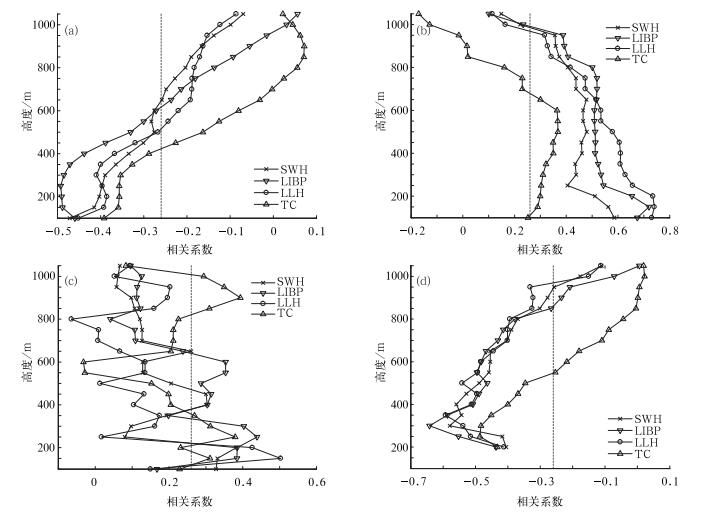
图 2是日平均NO₂浓度对数与风速对数、位温递减率、梯度理查森数、输送指数对数的相关系数。图中垂直虚线是相关系数通过α=0.05显著水平t检验时临界值。日平均NO₂浓度对数与风速对数呈负相关(图 2a)，4个环境监测站(SWH、LIBP、LLH和TC，下同)最大相关系数分别是-0.47、-0.49、-0.45和-0.39，LIBP在200 m高度相关系数最大，其余站点则在近地面50 m处相关系数最大。城区环境监测站在450 m以下相关系数均超过临界值，相关系数通过t检验；郊区环境监测站在350 m以下相关系数超过临界值。平均NO₂浓度对数与位温递减率呈正相关(图 2b)，4个环境监测站最大相关系数分别是0.59、0.72、0.74和0.37，城区150 m以下相关系数稳定，700 m以上相关性随高度增加迅速减小。城区环境监测站900 m以下相关系数均超过临界值，郊区环境监测站600 m以下相关系数超过临界值。日平均NO₂浓度对数与梯度理查森数呈正相关(图 2c)，4个环境监测站最大相关系数分别是0.38、0.44、0.50和0.39，但由于模式模拟的水平风场切变在垂直方向差异较大，垂直方向相关性波动明显。日平均NO₂浓度对数与输送指数呈负相关(图 2d)，4个环境监测站最大相关系数分别是-0.58、-0.64、-0.59和-0.49，500 m以上相关性随高度增加迅速减小。城区环境监测站在800 m以下相关系数均超过临界值，郊区环境监测站在450 m以下相关系数超过临界值。日平均PM₁₀浓度和风速、位温递减率、梯度理查森数、输送指数的相关性与NO₂相似(图略)。4个环境监测站日平均PM₁₀浓度与风速最大相关系数分别是-0.36、-0.44、-0.36和-0.25，与位温递减率最大相关系数分别是0.60、0.72、0.66和0.45，与梯度理查森数最大相关系数分别是0.56、0.39、0.53和0.30，与输送指数最大相关系数分别是-0.58、-0.56、-0.57和-0.47。表 2是日平均污染物浓度对数和稳定能量、Froude数对数及边界层高度的相关系数。稳定能量与污染物浓度呈正相关，城区相关系数超过0.5，最大相关系数是0.65。Froude数与污染物浓度呈负相关，相关性较差，最大相关系数是-0.53。边界层高度与污染物浓度呈负相关，兰州城区相关系数超过-0.6，最大相关系数是-0.78。受地形差异和污染源排放特征差异的影响，郊区气象条件与污染物浓度相关性低于城区。

平均而言，NO₂浓度与气象参数相关性较PM₁₀好，气态污染物受局地气象条件影响较颗粒物明显，这与Pearce等(2011b)研究结果一致。不同气象参数与污染物浓度的相关性差异明显，与污染物主要扩散和输送方式有关。兰州为典型的山谷城市，周边山体阻碍了城区大气与周边大气的交换(张强，2001)，城区位温递减率和边界层高度与污染物浓度相关性较其他参数好，污染物浓度主要受大气垂直扩散能力影响。

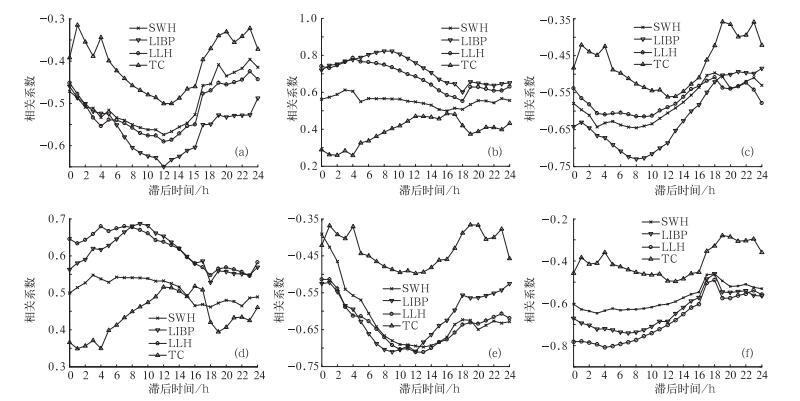
综合分析表明，50 m风速、100 m位温递减率和250 m输送指数与污染物浓度相关性较其他高度层显著。图 3是日平均NO₂浓度对数与50 m风速对数、100 m位温递减率、250 m输送指数对数、稳定能量、Froude数对数和边界层高度的相关系数随日平均污染物浓度计算的滞后时间的变化。从图中可以看出，气象条件对大气污染物浓度的影响有一定滞后性，24 h内相关系数随滞后时间基本呈现先增加后减小的变化趋势，但不同环境监测站、不同气象参数间相关系数极值出现的滞后时间不同。城区日平均污染物浓度计算比风速和Froude数滞后12 h左右时，其相关系数达到极值，如图 3所示，除风速和Froude数，城区站点(SWH、LIB和LLH)相关系数极值(极大值或极小值)滞后时间小于12 h，郊区则大于12 h。气象条件对12 h后大气污染物浓度的影响逐渐减弱。颗粒物来源复杂，气象参数与PM₁₀浓度相关系数达到极值时的滞后时间比气象参数与NO₂浓度相关系数达到极值时的滞后时间长(图略)。受地形、排放源差异的影响，城区各环境监测站气象条件对大气污染物浓度影响的滞后性也不同，除风速和Froude数，SWH站点气象参数与污染物浓度的相关系数达到极值的滞后时间是3~8 h，LIBP站点相关系数达到极值的滞后时间是7~11 h，LLH站点相关系数达到极值的滞后时间是4~8 h。郊区气象参数与污染物浓度达到极值的滞后时间是12~17 h，较长的滞后时间可能与兰州城区污染物向郊区输送有关。进一步分析发现，风速对大气污染物浓度影响的滞后性比温度层结明显。

2.3 回归方程建立

在污染特征及地形地貌基本不变、污染物排放相对稳定的情况下，利用气象条件对大气污染物浓度的影响有一定滞后性的特征，通过建立多元回归方程可以预测气象因素变化对大气污染物浓度的影响。

受地形和城市热岛影响，兰州城区出现大气层结不稳定概率高于郊区，当大气层结不稳定时，无法计算输送指数和Froude数。因此，在进行逐步回归分析时，城区选取50 m风速对数、100 m位温递减率、稳定能量和边界层高度，郊区选用50 m风速对数、100 m位温递减率、250 m输送指数对数、稳定能量、Froude数对数和边界层高度作为自变量，用污染物浓度对数作因变量，用2011年11月1日至2012年1月20日资料进行线性回归拟合。不同气象参数对大气污染物浓度影响的滞后性不同，分别选取4、8、4和12 h滞后时间计算SWH、LIBP、LLH和TC 4个环境监测站日平均NO₂浓度，再分别选取7、9、4和17 h滞后时间计算这4个环境监测站的日平均PM₁₀浓度，来建立预报模型。通过线性拟合，得到NO₂回归方程式(1)~式(4) 和PM₁₀回归方程式(5)~式(8)。回归方程均通过α=0.05显著性水平F检验，具有统计显著性。

$ \ln {\left( {\bar C} \right)_{{\rm{SWH}}}} = - 0.371\ln \left( {\bar u} \right) + 102.783\frac{{\overline {\partial \theta } }}{{\partial z}} - 3.001 $

(1)

$ \ln {\left( {\bar C} \right)_{{\rm{LIBP}}}} = - 0.202\ln \left( {\bar u} \right) + 151.787\frac{{\overline {\partial \theta } }}{{\partial z}} - 3.631 $

(2)

$ \ln {\left( {\bar C} \right)_{{\rm{LLH}}}} = 80.703\frac{{\overline {\partial \theta } }}{{\partial z}} - 0.00187\overline {Bh} - 2.99 $

(3)

$ \ln {\left( {\bar C} \right)_{{\rm{TC}}}} = - 0.412\ln \left( {\bar l} \right) - 1.533 $

(4)

$ \ln {\left( {\bar C} \right)_{{\rm{SWH}}}} = - 0.608\ln \left( {\bar u} \right) + 177.493\frac{{\overline {\partial \theta } }}{{\partial z}} - 2.13 $

(5)

$ \ln {\left( {\bar C} \right)_{{\rm{LIBP}}}} = 206.144\frac{{\overline {\partial \theta } }}{{\partial z}} - 0.0019\overline {Bh} - 2.443 $

(6)

$ \ln {\left( {\bar C} \right)_{{\rm{LLH}}}} = 89.039\frac{{\overline {\partial \theta } }}{{\partial z}} - 0.00309\overline {Bh} - 1.34 $

(7)

$ \ln {\left( {\bar C} \right)_{{\rm{TC}}}} = 0.000111{{\bar E}_{500}} - 3.422 $

(8)

式中，C是污染物日平均浓度(单位：μg·m^-3)，$\frac{{\overline {\partial \theta } }}{{\partial z}}$是100 m高度日平均位温递减率(单位：K·m^-1)，u是50 m高度日平均风速(单位：m·s^-1)，l是250 m高度日平均输送指数(单位：m)，E₅₀₀是地面到500 m高度日平均稳定能量(单位：J·m^-2)，Bh是日平均边界层高度(单位：m)。

表 3是4个环境监测站线性回归方程拟合度，城区(LIBP、LLH和SWH)回归方程拟合度高于郊区(TC)，LIBP站拟合度最高(0.713)。尚可政等(1999；2002)利用兰州城区环境监测站大气污染物浓度日均值和能见度、总云量、气压、气温、相对湿度和风速等气象观测资料建立线性回归模型，冬季NO_x回归方程拟合度在0.45~0.80之间，但回归方程预报精度高度依赖能见度和总云量，给实际大气污染物浓度预测带来不便。赵仲莲等(2006)基于地面气象要素和天气形势建立了兰州城区大气污染预报模型，冬季NO₂回归方程拟合度在0.33~0.47之间，PM₁₀回归方程拟合度在0.35~0.44之间。本文所选气象参数较全面，与污染物浓度相关性较高，回归方程拟合度高。

2.4 回归方程对污染物浓度的预报检验

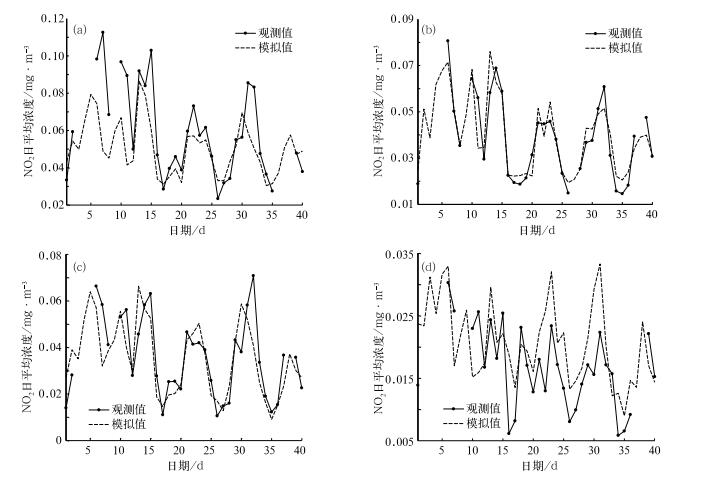
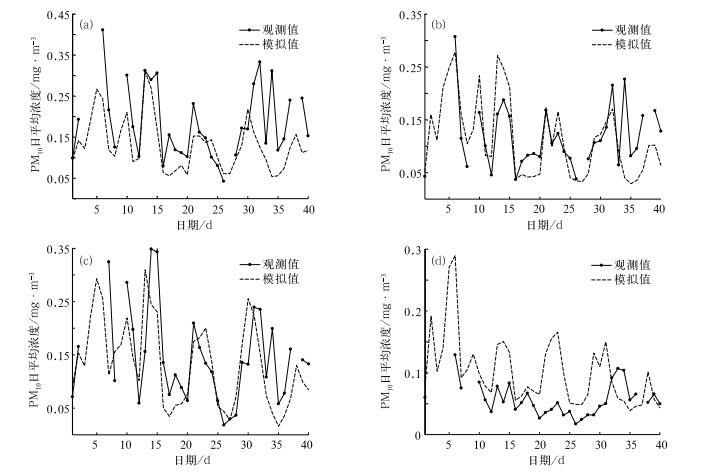
图 4和图 5是用回归方程预报得到的2012年1月21日至2月29日NO₂和PM₁₀的日平均浓度及其与观测结果的对比。其中，NO₂日平均浓度模拟值与观测值的相关系数和回归方程复相关系数相当，而PM₁₀日平均浓度模拟值与观测值的相关系数比回归方程复相关系数低(可能与春节前后大量燃放烟花导致PM₁₀浓度增加有关)，除TC站点外，其余站点由回归方程模拟的日均PM₁₀浓度均低于观测值(表 4)。城区回归方程拟合度好于郊区回归方程拟合度(表 3)，使回归方程对城区污染物浓度的预报效果好于郊区。TC站点模拟PM₁₀浓度与观测值相比偏差较大，可能是由于预测时段内PM₁₀浓度很低(基本与城区PM₁₀浓度最低值相当，代表该区域大气背景浓度)，局地气象条件对其浓度逐日变化的影响很小，进一步分析也证实预测时段TC站点PM₁₀日均浓度与局地气象条件相关性很低。由于资料限制，本文用于建立回归方程的资料时间序列较短，利用更长时间的资料作回归分析，结果应有所改善。

为进一步分析回归方程对污染物浓度的预报能力，下面用平均值(M)、相关系数(R)、均方根误差(RMSE)、标准差(SD)、归一化平均偏差(NMB)和归一化平均误差(NME)进行预报检验。表 4中由回归方程得到的NO₂日均值与观测的日均值之差小于10 μg·m^-3，但PM₁₀日均值与观测的日均值相差较大(SWH和TC两站误差分别达到58.3和37.3 μg·m^-3)。回归方程预报的日均NO₂浓度和PM₁₀浓度与观测值的相关系数在城区分别超过0.7和0.6，但对污染物浓度极值的模拟偏弱。整体而言，NO₂回归方程的模拟效果好于PM₁₀，回归方程对城区污染物浓度的模拟效果好于郊区。

目前，空气质量数值模式是模拟大气污染物浓度的主流方法，可较准确地模拟大气污染物的时空分布，但其模拟精度依赖于排放清单的精度，不同地区不同模式模拟性能差异较大。Sartelet等(2007)用Polyphemus系统模拟欧洲颗粒物和气态污染物浓度变化时得到的NO₂均方根误差为10~20 μg·m^-3，相关系数为0.3~0.4；PM₁₀均方根误差低于20 μg·m^-3，相关系数为0.4~0.6。Im等(2010)用WRF/CMAQ模拟研究了伊斯坦布尔冬季PM₁₀日平均浓度的变化，其观测和模拟平均值分别是107.1和96.4 μg·m^-3，标准差分别是15.1和19.7 μg·m^-3，均方根误差是24.5 μg·m^-3。Roustan等(2011)用化学输送模式(CTM)模拟了巴黎NO₂小时浓度和PM₁₀日平均浓度，得到NO₂和PM₁₀观测平均值分别是32.1和18.7 μg·m^-3，模拟平均值分别是24.4和22.7 μg·m^-3，相关系数分别是0.54和0.5，均方根误差分别是18.9和9.8 μg·m^-3，归一化平均误差分别是45.9%和40%，归一化平均偏差分别为-27.9%和22%。

本文利用WRF模式模拟的气象场，结合污染物浓度监测资料，分析研究建立的污染物浓度与气象影响因子的回归方程，其对污染物浓度的模拟效果与常用的空气质量数值模式模拟效果相当，回归方程对兰州城区污染物浓度的预测值与观测值相关系数、归一化平均误差和归一化平均偏差甚至好于数值模式模拟的效果。与空气质量数值模式相比，该方法不需要污染源排放数据，并且可用WRF模式预报的气象场预测污染物浓度水平，为城市空气质量预报、大气污染防治和研究提供了科学依据。

3 结论

本文利用WRF数值模式模拟的兰州市及其周边气象场，结合污染物浓度监测数据，分析了气象影响因素与污染物浓度之间的相关性，并建立了污染物浓度与气象影响因子的回归方程，得到以下结论：

(1) NO₂与气象影响因子的相关性较PM₁₀好。兰州城区污染物浓度与位温递减率和边界层高度相关性高。由于周边山体的阻挡作用，污染物浓度主要受垂直扩散的影响。

(2) 气象条件对大气污染物浓度的影响有一定的滞后性，24 h内相关系数随滞后时间基本呈现先增加后减小的变化趋势，风速对大气污染物浓度影响的滞后性比温度层结明显。

(3) 线性回归方程对NO₂浓度的模拟效果好于对PM₁₀的模拟效果，对城区污染物浓度的模拟效果好于对郊区污染物浓度的模拟效果。

(4) 线性回归方程对污染物浓度的模拟效果与常用的空气质量模式的模拟效果相当，回归方程对兰州城区污染物浓度的模拟效果甚至好于部分地区空气质量数值模式的模拟效果。

本研究结果为山谷城市大气污染物浓度预测提供了一种新方法，该方法比用空气质量数值模式计算快，模拟效果较好，可用于城市大气污染预报。

附  录：

式(1)~式(5) 分别给出了位温递减率、输送指数、梯度理查森数、Froude数和稳定能量的计算方法。

$ \gamma = \frac{{\partial \theta }}{{\partial z}} $

(1)

$ l = {u_z}/\sqrt {\frac{g}{\theta }\frac{{\partial \theta }}{{\partial z}}} $

(2)

$ {R_i} = \frac{g}{\theta }\frac{{\partial \theta }}{{\partial z}}\left[ {{{\left( {\frac{{\partial u}}{{\partial z}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial z}}} \right)}^2}} \right] $

(3)

$ Fr = \bar u/\left( {h\sqrt {\frac{g}{\theta }\frac{{\partial \theta }}{{\partial z}}} } \right) $

(4)

$ {E_w} = \frac{{{c_p}}}{g}\int_{{p_h}}^{{p_0}} {({T_G} - G){\rm{d}}p} $

(5)

式中，γ是位温递减率(单位：K·m^-1)，正值越大表示层结越稳定；θ是位温(单位：K)；z是高度(单位：m)；l是输送指数(单位：m)；u_z是高度z处水平风速(单位：m·s^-1)；g是重力加速度(单位：m·s^-2)；u和v是水平风速(单位：m·s^-1)；u是0~500 m平均水平风速(单位：m·s^-1)；h是山谷深度(单位：m)，取500 m；E_w是稳定能量(单位：J·m^-2)；c_p是定压热容(单位：J·K^-1·kg^-1)；T是温度(单位：K)；p是气压(单位：Pa)。