2. 中国气象科学研究院,北京 100081
2. Chinese Academy of Meteorological Sciences, Beijing 100081
云强烈地影响地气系统中的热力平衡和水循环过程,在全球气候及其变化中扮演重要角色。在对云辐射的研究中,云光学厚度τ和云粒子有效半径re是两个重要参数,鉴于它们对太阳反射和吸收性质的敏感性(Chandrasekhar,1960),可以通过可见光波段和近/中红外波段的反射率来分别反演。
传统的云粒子有效半径反演方案中假定存在垂直均一的平面平行云,即有效粒子半径不随高度变化。最有代表性的是由Nakajima等(1990)提出的利用0.75和2.16 μm通道同时反演云的光学厚度和云粒子有效半径的算法。NOAA-AVHRR(Advanced Very High Resolution Radiometer)发射后,3.7 μm通道被广泛用于反演云粒子的有效半径(Kaufman et al,1993;Han et al,1994;Platnick,2000;许健民等,2010;李俊等,2012),赵凤生等(2002)建立了一种利用AVHRR的0.64和3.75 μm通道测量的辐射率同时反演云的光学厚度和云滴有效半径的迭代方法,并将其应用于分析中国东海上空冬季层积云的辐射特性,刘健等(2003)利用FY-1C双通道资料同时反演水云的光学厚度和有效粒子半径。李娟等(2005)利用GMS-5静止卫星资料,通过模拟分析,提出了初步反演云顶部物理特性的方法,陈英英等(2007)基于SBDART(Santa Barbara DISORT Atmospheric Radiative Transfer)辐射传输模式,利用FY-2C第3.7 μm通道资料反演了水云粒子的有效半径,并与MODIS(Moderate Resolution Imaging Sepectroradiometer)的相应产品作了比较,发现两者具有较好的时空分布一致性。刘香娥等(2010)用SBDART辐射传输模式模拟计算了FY-2C中3.7 μm通道接收的总辐射、热辐射及散射辐射, 分析了它们的特性及对云粒子有效半径的敏感性, 提出了从该通道接收总辐射中扣除地面及云热辐射贡献项的经验关系式。
但理论和观测结果显示,云滴分布存在一定的垂直结构,如Slingo等(1982)等研究了海上积层云的飞机观测数据,发现云粒子半径和液水含量有垂直结构,黄梦宇等(2005)研究了大量飞机观测云滴谱资料,发现在层状云中,云滴有效半径从云底向上有增大的趋势。Chang等(2002)假定有效粒子半径在垂直方向上呈线性变化,并提出了用多个近红外通道选取最佳线性廓线的方法,还进一步提出,当云非常厚且云粒子有效半径廓线非线性时,对云底处有效粒子半径的计算会有很大的不确定性,因为卫星接收到的云底信号很弱。Chen等(2007)提出了一个用3.7、2.1和1.6 μm通道联合反演云粒子有效半径垂直廓线的方法并用此法提升了LWP的计算精度。
虽然3.7 μm波段被广泛用于云粒子有效半径的反演,但由于云粒子对该波段有很强的吸收,因此3.7 μm反射率只对靠近云顶的云粒子有效半径的变化敏感(Platnick et al,2000)。基于此,3.7 μm的反演方法对有效粒子半径垂直均一分布的云具有一定的合理性,对有效粒子半径垂直非均一的云,反演结果可能只代表云顶附近的一个浅层,而不能反演整层云的性质。
本文首先利用SBDART辐射传输模式,计算了不同有效粒子半径和光学厚度分布下的3.7 μm通道的反射率。具体设计了以下情形:(1) 有效粒子半径垂直连续变化分布;(2) 有效粒子半径垂直分层均一分布。此外,还通过有效粒子半径垂直非均一的云与有效粒子半径垂直均一的云进行反演结果的对比,计算了把后者当作前者反演时的误差,分析了影响该误差的因素。
1 工具介绍SBDART(Ricchiazzi, 1998)是一个用于计算平面平行大气条件下的辐射传输计算软件。在该计算程序中,散射、分子吸收和热辐射过程同时存在。SBDART包含了影响紫外、可见光和红外辐射场的各种重要过程, 集成了复杂的离散坐标辐射传输模块DISORT、低分辨率大气透射模式LOWTRAN和水滴、冰晶的米散射结果。该模式包含多流的算法, 参数的选择及自行设定比较方便。代码适用于各类大气辐射能量平衡和遥感方面的研究, 也可以用于进行敏感性实验, 最关键的是它提供了有关角度(如太阳天顶角、卫星天顶角和相对方位角等)和云微物理特征方面的辐射信息, 云参数的设定为计算卫星遥感的辐射量奠定了基础。
文中运用SBDART模式模拟计算有云状况下卫星中红外通道散射辐射值,需改动或设定的参数有:云层的高度h、光学厚度τ、云粒子有效半径re、太阳天顶角sza、卫星天顶角uzen、太阳与卫星之间的相对方位角phi、地表反照率albcon、计算辐射类型nothrm、大气廓线idatm、卫星通道响应函数isat、输出项选择iout等。
SBDART中,re垂直廓线函数如下:
| $ {r_e}\left(h \right) = {r_{e0}} \times {\left({\frac{{{r_{e1}}}}{{{r_{e0}}}}} \right)^{\left({h - {h_0}} \right)/\left({{h_1} - {h_0}} \right)}} $ | (1) |
其中h是高度,h0是云底高度,h1是云顶高度,单位为km。re0是云底处的有效粒子半径,re1是云顶处的有效粒子半径,单位为μm。
此外,模式中还可以设置每层均匀但多层叠加的情形。
2 有效粒子半径垂直分布对3.7 μm反射率的影响为了研究有效粒子半径的垂直分布对3.7 μm反射率的影响,本节利用SBDART辐射传输模式模拟云顶有效粒子半径为16 μm,云底有效粒子半径为不同值时的3.7 μm反射率。
2.1 不同有效粒子半径廓线下的3.7 μm反射率对于非降水的层状云,由于其垂直运动很弱,所以云粒子的增长主要依靠凝结而非碰并。在云底部,温度高,云滴凝结相对较少,而在云顶部,温度低,云滴凝结相对较多。因此对于非降水的层状云,云粒子尺度随高度增大。如Hallett等(1974)所述,对于明显的降水来说,云滴的有效半径至少要达到12 μm。基于上述理论,本节模拟非降水的层状云,云顶有效粒子半径为16 μm,设定云粒子有效半径随高度增加。由于卫星3.7 μm通道白天所测的辐射来自对太阳辐射的反射和自身的热辐射两个部分,后者在反演云粒子有效半径时实际上是一种干扰,要设法先去除掉,再用单纯的散射辐射的信息来反演。因此本文在计算时将计算辐射类型nothrm设置成1,即没有热辐射的情形。具体参数如表 1所示。
|
|
表 1 不同re分布下,计算3.7 μm反射率时的参数设置 Table 1 Parameter settings in the computation of the 3.7 μm reflectance (for different re profile) |
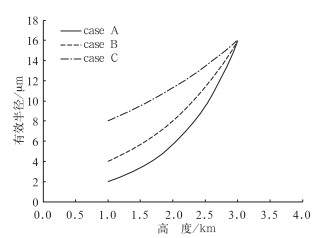
由式(1) 可知,当云顶、云底高度和云顶有效粒子半径恒定,云底有效粒子半径的不同对应不同的有效半径垂直廓线,这三种情况下,粒子有效半径随高度的变化曲线如图 1所示。
|
图 1 A、B、C三种情况下有效粒子半径随高度变化示意图 (A廓线:云底re为2 μm,云顶re为16 μm,B廓线:云底re为4 μm,云顶re为16 μm,C廓线:云底re为8 μm,云顶re为16 μm) Fig. 1 Changes of effective radius with height in three cases A, B and C |
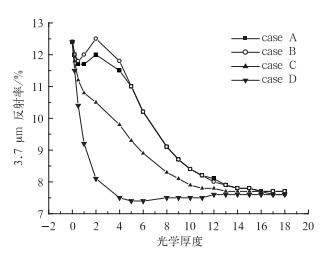
另外,取有效粒子半径随高度均一分布,且为16 μm的情况作为对比,记为廓线D。为了研究这四种re分布下云的辐射性质,将表 1中的参数输入SBDART辐射传输式计算不同光学厚度τ和这四种有效粒子半径垂直分布条件下的3.7 μm波段反射率,结果如图 2所示。
|
图 2 不同云粒子有效半径垂直分布条件下,云光学厚度与3.7 μm通道反射率的关系图 Fig. 2 Under the conditions of effective radius' different vertical distribution, the relationship between opitcal thickness and the 3.7 μm reflectance |
分析图 2可知,3.7 μm通道反射率受re垂直分布和云光学厚度的影响十分显著。case A和case B在光学厚度为0~1时,反射率下降,这是因为光学厚度为0时体现的是地表的反射率,随着云光学厚度的增加,对地表产生了遮挡(此时云的反射率小于地表反射率),因此此时反射率随着云光学厚度的增加而降低。case A和case B在光学厚度为1~3时,随着云光学厚度的增大,云的反射率也随之增加,这是因为随着云越来越密实,云体反射率增大。当光学厚度大于3时,随着云光学厚度的增大,云的反射率随之减小,这是因为随着云光学厚度的增加,卫星接收到的辐射是靠近顶层的大粒子的辐射,而大粒子的辐射偏小,导致反射率随光学厚度的增加而减小。对于case C和case D,由于这两种情况下云底有效粒子半径比前两种情况小很多,因此反射率也会比地表反射率小很多,综合看来,3.7 μm反射率随光学厚度的增加呈不断减小的趋势。综上所述,当光学厚度为0时,3.7 μm反射率体现的是地表的反射率,随着光学厚度的增大,3.7 μm反射率体现的是地表反射率和云反射率的综合结果,当光学厚度大到一定程度时,云体对地表完全遮挡,此时3.7 μm反射率体现的是云的反射率。
由不同颜色曲线的分离度可以看出,随着光学厚度τ的增加,有效粒子半径垂直廓线的变化对3.7 μm通道反射率的影响先增大后减小。经初步计算,当τ=10时,四个反射率值的均方差为0.0028,因此可以认为当τ≥10时,有效粒子半径垂直廓线的变化对3.7 μm通道反射率无影响。这说明对于3.7 μm通道,当τ很大时,只有云顶部粒子的辐射才能被卫星接收,故此时该通道反射率只能反映云顶附近的有效粒子半径情况,与有效粒子半径垂直分布关系不大。当0<τ<10时,云顶与云底粒子有效粒子半径相差越大,对反射率的影响也越大,这说明此时3.7 μm通道反射率可以反映有效粒子半径的垂直分布。
2.2 与re垂直均一分布云的对比为了进一步研究云粒子有效半径垂直廓线的分布对3.7 μm反射率的影响,本节把图 1中A、B、C三条廓线情况下云的反射率跟re垂直均一云的反射率作了对比,如表 2所示,并分别反演出把具有A、B、C三种re垂直廓线的云当做re垂直均一分布时反演所得到的re值,如表 3所示,进一步分析把具有re垂直非均匀的云当做re垂直均一分布时所带来的反演误差。
|
|
表 2 不同光学厚度和re垂直分布时的3.7 μm反射率值(单位:%) Table 2 The 3.7 μm reflectance for different opitcal thickness and re vertical distribution(unit:%) |
|
|
表 3 不同光学厚度和re垂直分布时对应的re垂直均一云的re及误差(括号中为误差, 单位:%) Table 3 The results and errors (in brackets, unit:%) for different optical thickness when taking the re in vertical inhomogeneous cloud as the re in homogeneous cloud |
当光学厚度太小时,在3.7 μm通道反射率易受到地面辐射的干扰,而光学厚度很大时,三种情况的反射率值已经很接近,无法揭示其垂直分布特征,因此只讨论光学厚度在4~10的情况。
由表 2和3可以看出,对于廓线A、B、C,随着光学厚度的增加,反射率值将越来越接近廓线D,将之当作re垂直均一反演时所得到的re值也更加接近16 μm,即云顶部的有效粒子半径值,表 3中的相对误差随着光学厚度从23.8%下降到7.5%进一步说明了这一点。当光学厚度一定,re垂直分布不同时,云顶与云底re相差越小,则反演误差越小。
3 3.7 μm反射率对有效粒子半径垂直深度上的反映能力 3.1 “有效辐射层”的提出及其光学厚度的计算为解决利用3.7 μm波段反演有效粒子半径垂直非均一的云时遇到的问题,即仅能反演云顶附近一个浅层的情况,结合光子在层状云中的传输理论(Platnick,2000),定义当云的光学厚度比较大时,云顶附近能被反演到的云层为有效辐射层。通过有效辐射层的大小,可以定量地描述利用3.7 μm波段反演有效粒子半径垂直非均一的云有效粒子半径时究竟反演了多厚的一层云。
由于有效辐射层以下的云辐射并不能被遥感仪器(如卫星)接收,因此这些云粒子的粒子尺度信息不能被反演。为了定量区分有效辐射层和非有效辐射层,把有效辐射层的光学厚度记为τs。如果云层总的光学厚度为τ,则非有效辐射层的光学厚度为τ-τs。为了计算有效辐射层的光学厚度τs,用SBDART辐射传输模式做了数值模拟,下面介绍具体方法。
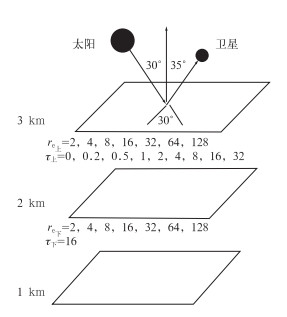
3.2 实验设计如图 3所示,设定一层云,其云底高度为1 km,云顶高度为3 km,在2 km处把云分为上下两部分。需要输入SBDART的参数如表 4所示。
|
图 3 实验设计示意图 Fig. 3 The schematic diagram of experimental design |
|
|
表 4 计算有效辐射层光学厚度时的参数设置 Table 4 Parameter settings in the computation of the effective radiation layer |
如此输入,则输出值为不同上部有效粒子半径、上部光学厚度和下部有效粒子半径下的3.7 μm反射率。
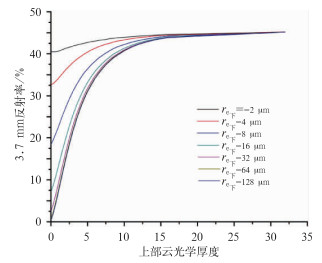
3.3 计算方法在计算时,先把上部云的有效粒子半径固定,再计算上部云的光学厚度不同时,下部云的有效粒子半径re下[k](k取1~7) 的变化对3.7 μm反射率R3.7[i, j, k]的影响。图 4是上部云的有效粒子半径为2 μm,下部云的有效粒子半径分别取2、4、8、16、32、64和128 μm时,反射率值随上部云光学厚度的变化图。
|
图 4 下部云有效粒子半径变化时,反射率与上部云光学厚度关系图 Fig. 4 The relationship between the upper layer's opitcal thickness and the 3.7 μm reflectance when the effective radius in the lower layer of cloud changes |
由图 4可以看出:
(1) 当上部云光学厚度较小时,大气上界观测到3.7 μm的反射率对下部云有效粒子半径变化是很敏感的。但随着上部云光学厚度逐渐增大,这种敏感性就越来越弱。到上层云的光学厚度达到一定值时,无论下层云的有效半径有什么变化,云顶的反射率已经对它完全没有响应,也就是说,大气上界观测到的3.7 μm反射率仅仅取决于上层云了,这一层即为有效辐射层。
(2) 计算表明,当上层云的有效半径不同时,有效辐射层对应的光学厚度不同。
上部云光学厚度一定时所对应的7个反射率值的标准差定义为:
| $ \varepsilon = \sqrt {\frac{{\sum\limits_{i = 1}^7 {{{\left({{R_i} - \bar R} \right)}^2}} }}{7}} $ | (2) |
式中,Ri代表 3.7 μm波段反射率,R是7个反射率的平均值。
为了定量地判定有效散射层的光学厚度,参考图 4,用式(2) 计算当上层云取不同光学厚度(即图 4的x轴)时,下层云有效半径的变化引起云顶反射率变化的均方差,而且规定当均方差小到0.003时,上层云的厚度即为有效辐射层的厚度。下面讨论影响τs的因素。
3.4 云顶有效粒子半径对有效辐射层光学厚度的影响按照3.3中的方法,分别计算了上部云有效粒子半径为2、4、8、16、32和64 μm,ε=0.003时的上部云光学厚度值,结果如表 5所示。
|
|
表 5 云顶有效粒子半径不同时的有效层光学厚度值 Table 5 The effective radiation layer's optical thickness versus the upper layer's effective radius |
分析表 5可知,随着云顶有效粒子半径的增大,τs减小。这说明有效粒子半径很小时,需要一层光学厚度较大的云才能达到完全不透明,以抵挡下面一层云的辐射对其云顶处辐射的干扰;而当有效粒子半径较大时,只要光学厚度较小的一层云就能达到完全不透明。粗略看来,该结果似乎与传统理论有悖。根据粒子散射相关理论,云滴有效半径越小,云的反射能力越强,云滴有效半径越大,云的反射能力越弱。按照此理论,有效粒子半径小的云应该在光学厚度比较小的时候就达到完全不透明,而有效粒子半径大的云应该在光学厚度比较大的时候才能达到完全不透明。其实传统理论所说的“粒子有效半径减小,将导致云滴数密度增加,这时云的辐射率会增加”是基于垂直液态云水含量恒定这一前提, 但本实验并没有对垂直液态云水含量作定量限制。根据大气辐射有关知识,当云粒子尺度参数x增大到一定值时, 消光效率Qex的值趋向于2,另外,此节中re不随高度变化,在此条件下垂直液态云水含量的表达式为
| $ LWP = \frac{2}{3}{\rho _w}{r_{\rm{e}}}\tau $ | (3) |
由式(3) 可知,液水路径LWP与有效半径和光学厚度的乘积成正比,本节中re与τ乘积并非为一定值。通过表 5也可发现与有效层光学厚度相关的液水路径LWP并非定值。随着有效粒子半径的增加,有效层光学厚度亦增加,因此这两者乘积迅速增大,液水路径LWP的值也随之增大。
综上所述,当有效粒子半径小时,有效辐射层需要的云水量较小,有效辐射层光学厚度较大;当有效粒子半径大时,有效辐射层需要的云水量较大,有效辐射层光学厚度较小。
3.5 散射几何角度对有效辐射层光学厚度的影响 3.5.1 太阳天顶角对有效辐射层光学厚度的影响3.4节中讨论的是太阳天顶角为30°,卫星天顶角为35°,相对方位角为30°时的结果。为了研究3.4中的结论是否具有普遍性,本节计算不同散射几何角度时的有效辐射层光学厚度。
设定卫星天顶角为5°,相对方位角为0°,太阳天顶角分别为0°、30°和60°,其他参数与表 1中设置相同,有效辐射层光学厚度计算的具体结果如表 6所示。
|
|
表 6 不同太阳天顶角时的有效层光学厚度值 Table 6 The variations of effective radiation layer's optical thickness with the solar zenith angles |
可以发现,对于任意的太阳天顶角,随着上部云有效半径的加大,有效辐射层的光学厚度都变小,与3.4中结论一致。当上部有效粒子半径相同时,随着太阳天顶角增大,有效辐射层的光学厚度减小。这是因为对于同样光学厚度的云,太阳天顶角越大,光线在云中经过的路径越长,所需要的有效辐射层的光学厚度越小的缘故。
3.5.2 卫星天顶角和相对方位角对有效辐射层光学厚度的影响设定太阳天顶角为30°,上部云有效粒子半径为2 μm,卫星天顶角分别取0°、5°、15°、25°、35°、45°、55°和65°,相对方位角从0°~180°每隔15°取一个值。所计算的有效辐射层光学厚度结果如图 5所示。
|
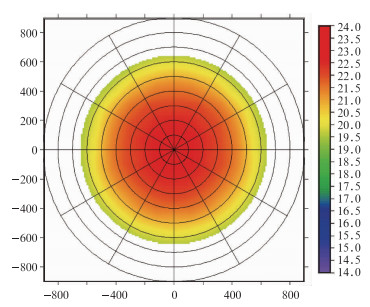
图 5 卫星天顶角和相对方位角不同时有效辐射层的光学厚度值 Fig. 5 The effective radiation layer's optical thickness as the function of satellite zenith angle and the relative azimuth angle |
图 5中极坐标的径向为卫星天顶角,每一个圈为10°;切向角度为观测方向和太阳入射方向的相对方位角;颜色代表有效散射层的光学厚度值。从图中可以看到,随着卫星观测天顶角的加大,有效辐射层的光学厚度值有减小的趋势,这是因为天顶角加大,倾斜路径的散射会更强,而本文所定义的有效散射层光学厚度是指一层云的垂直光学厚度。当卫星天顶角一定时,相对方位角的变化对有效辐射层的光学厚度影响不明显。
4 结论及讨论为进一步了解3.7 μm波段在反演云粒子有效半径中的作用,基于SBDART辐射传输模式,计算了不同有效粒子半径垂直分布时的3.7 μm反射率。
当有效粒子半径垂直非均一分布时,计算了不同云粒子有效半径垂直廓线时3.7 μm通道的反射率,通过反射率与光学厚度的变化趋势,进一步证明了有效辐射层的存在。通过与有效粒子半径垂直均一云的反射率的对比,发现当光学厚度小于10时,把有效粒子半径垂直非均一的云当作垂直均一的云进行反演时,云顶有效粒子半径的结果会出现一定的误差,该误差随着光学厚度的增大而减小,当云足够厚(光学厚度大于10) 时,该误差小于10%,由于反演时只能反演到云顶部粒子的信息,云底部粒子的信息不能被遥感仪器接受,所以此时云粒子有效半径的垂直分布的改变对3.7 μm反射率不再产生影响。
当有效粒子半径分为上下两层时,发现随着上层光学厚度的增大,下部有效粒子变化对3.7 μm反射率的影响逐渐减小。提出了有效辐射层光学厚度的概念并进一步分析了影响其大小的因素,结果表明,云顶部有效粒子半径越大,有效辐射层的光学厚度越小;随着太阳天顶角增大,有效辐射层的光学厚度减小;随着卫星天顶角的增大,有效辐射层的光学厚度减小;相对方位角的变化对有效辐射层的光学厚度影响不明显。通过对有效辐射层的定量计算结果得出,对于有效粒子半径大于4 μm的云,有效辐射层的光学厚度大致在3~10之间。
陈英英, 周毓荃, 杨军, 2007. 利用FY-2C静止卫星资料反演云粒子有效半径的试验研究[J]. 气象, 33(4): 29-34. DOI:10.7519/j.issn.1000-0526.2007.04.005 |
黄梦宇, 赵春生, 2005. 华北地区层状云微物理特性及气溶胶对云的影响[J]. 南京气象学院学报, 28(3): 360-368. |
李娟, 毛节泰, 2005. GMS卫星资料反演云的物理特性及其在人工影响天气中的应用[J]. 气象学报, 63(增刊): 47-55. |
李俊, 方宗义, 2012. 卫星气象的发展—机遇与挑战[J]. 气象, 38(2): 129-146. DOI:10.11898/1001-7313.20120201 |
刘健, 董超华, 张文建, 2003. 利用FY-1C资料反演水云的光学厚度和粒子有效半径[J]. 红外与毫米波学报, 22(6): 436-440. |
刘香娥, 王广河, 2010. FY-ZC静止气象卫星红外通道辐射特性研究[J]. 气象, 36(2): 39-47. DOI:10.7519/j.issn.1000-0526.2010.02.006 |
许健民, 杨军, 张志清, 等, 2010. 我国气象卫星的发展与应用[J]. 气象, 36(7): 94-100. DOI:10.7519/j.issn.1000-0526.2010.07.016 |
赵凤生, 丁强, 孙同明, 等, 2002. 利用NOAA-AVHRR观测数据反演云辐射特性的一种迭代方法[J]. 气象学报, 60(5): 594-601. DOI:10.11676/qxxb2002.070 |
Chandrasekhar S.1960.Radiative Transfer.N.Y:Dover.
|
Chang F L, Li Z, 2002. Estimating the vertical variation of cloud droplet effective radius using multispectral nearinfrared satellite measurements[J]. J Geophys Res, 107: 4257. DOI:10.1029/2001JD000766 |
Chen R, Chang F L Z, Li R F, et al, 2007. Impact of the vertical variation of cloud droplet size on the estimation of cloud liquid water path and rain detection[J]. J Atmos Sci, 64(11): 3843-3853. DOI:10.1175/2007JAS2126.1 |
Hallett J, Mossop S C, 1974. Production of secondary ice particles during the riming process[J]. Nature, 249: 26-28. DOI:10.1038/249026a0 |
Han Q, Rossow W B, Lacis A A, 1994. Near-global survey of effective droplet radii in liquid water clouds using ISCCP data[J]. J Climate, 7(4): 465-497. DOI:10.1175/1520-0442(1994)007<0465:NGSOED>2.0.CO;2 |
Kaufman Y J, Nakajima T, 1993. Effect of Amazon smoke on cloud microphysics and albedo-analysis from satellite imagery[J]. J Appl Meteor, 32(4): 729-744. DOI:10.1175/1520-0450(1993)032<0729:EOASOC>2.0.CO;2 |
Nakajima T, King M D, 1990. Determination of the optical thickness and effective particle radius of clouds from reflected solar radiation measurements. Part Ⅰ: Theory[J]. J Atmos Sci, 47(15): 1878-1893. DOI:10.1175/1520-0469(1990)047<1878:DOTOTA>2.0.CO;2 |
Platnick S, 2000. Vertical photon transport in cloud remote sensing problems[J]. J Geophys Res, 105(22): 919-935. |
Ricchiazzi P, 1998. SBDART: A research and teaching software tool for plane parallel radiative transfer in the earth's atmosphere[J]. Bull Amer Meteor Soc, 79(10): 2101-2114. DOI:10.1175/1520-0477(1998)079<2101:SARATS>2.0.CO;2 |
Slingo A, Nicholls S, Schmetz J, 1982. Aircraft observations of marine stratocumulus during JASIN[J]. Q J R Meteorol Sot, 108(458): 833-856. DOI:10.1002/(ISSN)1477-870X |
 2013, Vol. 39
2013, Vol. 39 
