引言

长期完整的气温日值序列，是大气环流模式、陆面过程模型等模式所需要的输入参数，并且是进行气候统计分析和气候变化研究的基础。但是，由于站址迁移、台站撤并、观测仪器故障以及其他历史原因等，造成气温观测数据缺测或长时间序列中断，从而引起台站日气温序列不完整，而序列的不完整将对气候变化及其趋势研究、气候评估及影响评价产生影响^[1]。因此，有必要对缺测的台站日气温资料进行估值计算，即对不完整的气温序列进行插补。

早在20世纪50年代，么枕生^[2]即提出了气温观测序列的订正问题。屠其璞^[3]对气温序列的延长和插补进行了相关分析与研究。近年来，我国研究人员利用一维车贝雪夫多项式展开、线性回归、逐步回归、偏最小二乘回归等方法对我国部分地区的气温月、年值资料进行了恢复性试验^[4-7]。此外，江志红等^[8-9]、张永领等^[10]对区域的气温场资料进行了插补研究。对台站观测的气温序列进行插补时，如果某站出现非连续的日气温缺测，可利用缺测日前后的气温数据进行插值计算，但是如果出现连续数日的气温缺测，应用该方法将造成较大误差^[11]。标准序列法^[12]是一种利用周边台站观测值进行插补的方法，它假设对于在同一气候区域内的所有站点，某日气温与该日多年平均气温的距平都是相似的。DeGaetano等^[13]对该方法进行了改进，并基于美国东北部近400站的气温资料，对日最高、最低气温缺测值进行了插补。王海军等^[14]利用DeGaetano等的方法，利用湖北省蔡甸站周边7个台站的资料，对该站非缺测的日平均、最高、最低气温进行了插补试验，取得了较好的插补效果。

本文利用DeGaetano等的标准序列法，对1971—2000年我国2000多个国家级地面气象台站的日平均气温进行插补试验，并用交叉检验方法^[15]验证其结果。使用标准序列法插补时，关键在于插补邻近站的选取。本文分别采用了“相关性最好”和“距离最近”两种邻近站选取方案，对比了两种方案的插补效果，同时对邻近站数的选择进行了讨论，并分析了不同台站其插补误差的大小与其邻近站平均距离之间的关系。

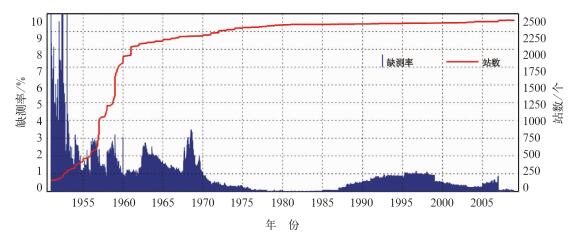
1 资料与方法 1.1 资料

本文利用了中国地面2400台站气候资料日值数据集(2.0版)^①中的日平均气温数据，该数据已经通过气候界限值、台站气候极值、内部一致性和时间一致性等质量控制方法的检验。从地面2400台站日平均气温缺测率统计分析来看(见图 1)，1970年前缺测相对较多，平均每月约有37站左右资料的缺失，20世纪90年代由于某些台站未将地面月报文件上报国家气象信息中心，造成了部分站整月缺测。为了较好地检验插补效果，选用了1971—2000年30年日平均气温序列进行插补试验。

^①中国气象科学数据共享服务网，http://cdc.cma.gov.cn.

1.2 插补方法

本文采用的插补方法为标准序列法^[12]，计算时，首先假设待插补站某年中的第i日日平均气温缺测，然后利用邻近站日气温标准化距平，对插补站的气温值进行估计，该方法可表示为：

${{Z}_{j}}=\frac{{{X}_{j}}-{{{\bar{X}}}_{j}}}{{{S}_{j}}}$

(1)

${{Z}_{\text{avg}}}=\frac{1}{n}\sum\limits_{j=1}^{n}{{{Z}_{j}}}$

(2)

${{X}_{i}}={{Z}_{\text{avg}}}{{S}_{i}}+{{{\bar{X}}}_{i}}$

(3)

式(1)~(3) 中，Z表示标准化序列，Z_avg为邻站平均标准化序列，j代表第j个邻近站，X_j为j站第i日日平均气温，X_j和S_j分别为j站第i日日平均气温的多年(本文中即为30年)平均值和标准差，n表示邻近站站数，X_i表示第i日待插补日气温，X_i和S_i分别为待插补站第i日日气温多年的平均值和标准差。

在插补前，首先建立了待插补站的邻近站表Cls_sta0。在选择邻近站时，以待插补站为中心，在距其220 km的范围内进行搜索，并且备选站的海拔高度应满足：

当h₀<2500 m时，|h-h₀| ≤200 m；

当h₀≥2500 m时，|h-h₀| ≤500 m；

式中，h₀、h分别为待插补站和备选站的海拔高度。选择与待插补站距离最近的20个站为该站的邻近站，若邻近站数不足20个，以实际数为准。

在插补试验中，基于邻近站表Cls_sta0设计了相关性最好(RO方案)和距离最近(CS方案)两种不同的邻近站选取方案。采用RO方案时，需首先计算各邻近站与待插补站日平均气温序列的相关系数，然后选取相关性最高的n个邻近站参与计算；而CS方案则选取与待插补站距离最近的n个邻近站参与计算。

1.3 检验方法

本文采用交叉检验方法对上述两种邻近站选取方案的结果进行对比分析，并用平均绝对误差(MAE)、均方根误差(RMSE)、插补值与实际观测值误差在±0.5℃范围内的样本比例(p)3项指标来考查插补精度和插补效果。当邻近站数为n时，MAE_n、RMSE_n和p_n的计算公式分别为：

$MA{{E}_{n}}=\frac{1}{m}\sum\limits_{i=1}^{m}{|{{x}_{ei}}-{{x}_{oi}}|}$

(4)

$RMS{{E}_{n}}=\sqrt{\frac{1}{m}\sum\limits_{i=1}^{m}{{{({{x}_{ei}}-{{x}_{oi}})}^{2}}}}$

(5)

${{p}_{n}}=\frac{{{m}_{p}}}{m}\times 100%$

(6)

式中，x_ei为第i日插补值，x_oi为第i日实际观测值，m为插补天数，m_p为插补值与实际观测值误差在±0.5℃范围内的天数。MAE和RMSE的值越小，且比例p越大，则表明插补精度越高。

2 结果分析

针对1971—2000年2088个国家级台站的日平均气温，分别采用RO和CS两种邻近站选取方案进行了插补试验。基于插补结果，分别统计了每个待插补站其邻近站数为n时的MAE、RMSE和比例p三项指标。

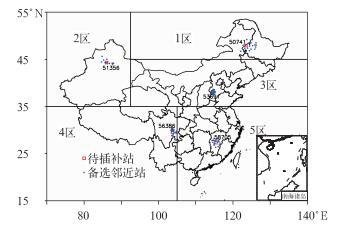
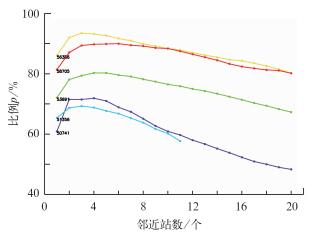
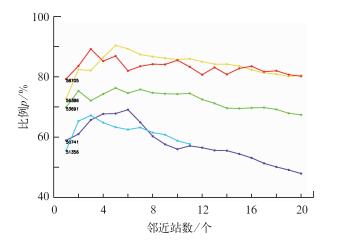
参考《中国气候总论》^[16]将全国大致划分为5个气候区(图 2)，在5个气候区中，分别随机选择了邻近站数相对较多的1个待插补站点，以上述统计指标p为例，给出了采用两种方案的不同插补精度，如图 3和4所示。当采用RO方案时，5个站的比例p随邻近站数增加均先增大后减小，呈现单峰变化。采用CS方案时，比例p随邻近站数的变化不尽相同，53691站的比例p随着邻近站数的增加变化不大，而58705站的比例p呈现出了多个峰值。对比发现，采用CS方案时5个站的比例p的最大值，比RO方案均有不同程度的减小。此外还可以看出，采用RO方案时，比例p在邻近站数为3~4时，即达到相对最大值，而采用CS方案时，比例p随邻近站数的变化没有规律性，达到相对最大值时的邻近站站数取值不固定。

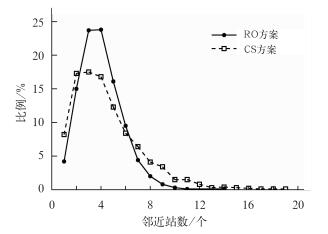
对所有被插补的台站，分别统计了MAE、RMSE达到相对最小，比例p达到相对最大时的邻近站数取值，同样以比例p为例给出了两种方案的对比结果，如图 5所示。当采用RO方案，约47.5%的台站当其邻近站数取为3或4时，比例p达到相对最大，约88.1%的台站邻近站数取值在2~6之间比例p达到相对最大。而采用CS方案，约72.3%的台站邻近站数取值在2~6之间时，比例p达到相对最大。由此可见，采用RO方案时的邻近站数取值相对比较集中。对比MAE和RMSE两项指标，也有类似的结论。

当邻近站数取为4(2~6的中值)时，对完成插补台站的MAE、RMSE和比例p进行了分区统计，并对比了两种方案的差异，结果在表 1中给出。在5个不同气候区采用RO方案的3项指标的平均值均好于CS方案，并且各气候区中超过85%的台站的3项指标RO方案优于CS方案。因此认为RO方案比CS方案的插补精度更高，在实际插补过程中应采用这一方案。对比不同气候区的插补精度可以看出，气候区5内的台站气温插补精度相对较高，MAE为0.340℃，而气候区2内的台站气温插补精度相对较低，MAE为0.672℃，这与不同气候区内台站的疏密有一定关系，将在第3节进行讨论。

综上所述，在实际使用标准序列法进行气温插补时，应选用RO方案，并且对于备选邻近站数较多的待插补站点，并不需要利用所有的邻近站资料来进行插补，只需要选择与待插补站相关系数最高的4个邻近站资料参与计算，这样得到的插补结果具有相对较高的插补精度。

3 邻近站距离对插补效果的影响

从表 1分区统计结果和图 3可以看出，利用标准序列法对不同台站日平均气温的插补精度存在差异。一般来说，如果邻近站与待插补站的距离较近且海拔高度相差不大时，两者的日平均气温序列相关性较高，利用标准序列法做插补计算，可以得到较高的插补精度。假设插补计算某站第i日日平均气温时，最相关的4个邻近站与待插补站的平均距离为d_i，则完成对m天日平均气温插补后的邻近站平均距离d_mean为：

${{d}_{\text{mean}}}=\frac{1}{m}\sum\limits_{i=1}^{m}{{{d}_{i}}}$

(7)

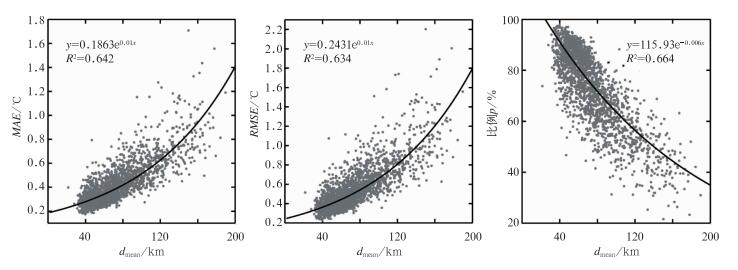
对2000多个国家级台站应用RO方案进行插补试验后的MAE、RMSE和比例p, 这3项插补精度指标，与d_mean求取拟合关系式，如图 6所示。可以看出，MAE和RMSE随d_mean增加呈e指数增大，而比例p随d_mean增加呈e指数减小，3项插补精度指标与d_mean的相关性约为0.8左右，通过了显著性检验。这样，由图 6中的3个拟合关系式，可以初步估计不同邻近站不同平均距离情况下的插补精度。但是，图 6中的关系式是通过对大量插补样本进行统计后的结果拟合而成，不适用于对单个插值结果进行精度评估。

4 结论

基于我国地面2000多台站日值气候资料，利用标准序列法，进行了日平均气温插补试验，得到以下结论：

(1) 当利用标准序列法进行日平均气温插补时，采用相关性最好方案选取邻近站的插补结果优于距离最近方案。

(2) 对插补站某年第i日日平均气温进行插补时，选取与待插补站历史同期日平均气温序列相关性最高的4个邻近站参与插补计算，这样得到的插补值具有较高的精度。从我国地面2000多台站日平均气温插补试验结果来看，插补值与实际观测值的平均绝对误差为0.424℃，均方根误差为0.551℃。

(3) 采用相关性最好方案时，MAE、RMSE、比例p与实际插补时所用的邻近站和待插补站的平均距离d_mean有较好的相关性，MAE和RMSE随d_mean的增加呈e指数增大，比例p随d_mean增加呈e指数减小。