引言

雷暴是一种灾害性天气，由于雷暴的时空尺度以及发生概率都较小，因此雷暴一直是预报中的重点和难点。现阶段，对雷暴常见而有效的预报手段主要有卫星、雷达等实况资料的外推以及天气学概念模型等方法，即雷暴预报的预报时效及有效性仅仅适用于雷暴的临近预报^[1-4]，而雷暴的短期预报却仍属于较难预报的范畴。随着数值模式的发展和模式产品精度相应的提高，模式产品的释用为雷暴短期预报准确率的提高提供了一种很好的解决途径。

模式产品的释用主要是建立预报对象与预报因子之间的关系。在模式既定的情况下，预报效果的提高与预报因子的选择和对象，以及因子之间关系的形式有关。近年来，因子分析技术在释用预报中已经有了较为成熟的应用；同时一些较好的建模新方法也在解释应用领域得到引进，比如逻辑回归判别、神经网络和支持向量机等方法。其中支持向量机方法在被冯汉中等^[5]引入到气象领域之后，在暴雨、大雾等的预报中均有较为成功的应用^[6-7]。

本文以在暴雨预报表现良好的AREM模式产品和常规观测报文为基础，运用支持向量机方法以及主成分分析技术，建立单站的雷暴MOS预报模型。

1 预报流程的前处理 1.1 资料介绍

AREM模式基于中国科学院大气物理研究所大气科学和地球流体力学国家重点实验室发展的REM η坐标暴雨数值预报模式^[8]。本文所用版本为AREM V2.4，模式分辨率是37 km，垂直层次22层，模式顶高20 hPa，积分区域为14°~51°N、74°~136°E。模式的初始场为NCEP再分析场与常规报文资料的融合。模式起报时间为当日世界时00 UTC(下同)，积分时间为36 h，模式产品输出间隔为6 h。鉴于E网格特点，其输出产品的分辨率0.5°×0.5°。在该模式中，云和降水过程采用BIAM显式冷云微物理过程方案和改进的Betts对流调整方案，行星边界层过程采用非局地边界层参数化方案，辐射方案采用基于Benjamin理论的MM5辐射方案，地表通量处理方案采用多层结通量廓线方案。

本文使用的资料为2002—2007年汛期5—8月的AREM模式产品和同期的常规观测报文资料，预报时效为12~36 h，其中建立模型时间为2002—2006年，预报试验的时间为2007年。

1.2 雷暴指标的介绍与计算

论文中采用的指标分为4类，合计72个。

(1) 模式输出量：地面温度和气压；高空温度、露点、风场、散度、涡度、垂直速度和位势高度，其中高空量有850、700、500和300 hPa 4层。这4层代表着低(850 hPa)、中低(700 hPa)、中(500 hPa)和高空(300 hPa)。

(2) 能量指标^[9]：对流有效位能(CAPE)、最优对流有效位能(BCAPE)、下沉对流有效位能(DCAPE)、对流抑制能(CIN)、925 hPa总能量(TEI₉₂₅)、850 hPa总能量(TEI₈₅₀)。

(3) 不稳定度指标^[9]：Adedokun 1指数、Adedokun 2指数、Rackliff指数、Boyden指数、Bradbury指数、Cross Totals指数、Vertical Total指数、Total Total指数、Lifted指数、K指数、Showalter指数、Potential Instability指数、S指数、Jefferson指数、Humidity指数、Deep Convective指数、KO指数、Thompson指数、自由对流高度、平衡高度、0℃层高度和Δθ_se。

(4) 综合指标^[9]：Severe Weather Threat指数、SWISS00指数、SWISS12指数、Yonetani指数、Modified Yonetani指数、Storm Relative Helicity指数、Energy Helicity指数、Storms Severity指数、Bulk Richardson Number指数和Wind指数。

由于后续的建模是针对站点，因此，因子的计算按照以下规则进行：(1) 考虑到雷暴量变到质变的积累过程和常规报文的6 h间隔，这里选择预报时刻和预报前一时刻的加权和进行因子场的计算，权重值以预报时刻为主。(2) 雷暴往往发生在站点附近地区，对于某一站点，雷暴指标除了该站点外还需要考虑到站点周围的格点。这里模式产品的水平分辨率近似50 km×50 km，雷暴的水平尺度也就数10 km，因此仅选择距离站点最近的两个格点。论文中站点的雷暴指标值采用周围4个格点的距离加权平均进行插值处理。

1.3 样本和因子的处理

雷暴属于小概率事件，小概率事件的预报建模一般都要求样本集的尽量均衡。在小概率天气现象样本集的均衡中，首先需要考虑样本的消空，消空的实现一般借用消空指标库的建立。通过试验发现：如果采用多个消空因子进行消空预报时，很容易错过有雷暴的天气。因此，这里仅采取1个消空因子作为消空的条件。

正常情况下，对于雷暴样本筛选和均衡，单靠因子消空还是不够的。在同类中，从多到少，或选择压缩，或选择提取。鉴于计算的简便实用，这里采用K-平均聚类^[10]的方法进行样本的压缩。由于K-平均聚类算法中初始聚类中心的选取是随意的，但是初始聚类中心的选取却又直接影响到样本压缩的效果，因此初始聚类中心的选取采用袁方等^[11]的初始聚类中心的选择算法。

因子的筛选分为初选和精选，由于消空的过程中某些重要对流参数的影响容易被覆盖掉，因此不再运用消空因子作为预报因子，而是采用F-分值^[10]进行因子的初选。F-分值思想来源于Fisher判别，即实现同类之间差别小，异类之间差别大。具体选择时，给定初选因子的个数d，把各个对流参数的F-分值按降序排列，然后找出前d个最大值对应的下标，这些下标对应的对流参数就作为初选的因子。

鉴于主成分分析较为常见，因此这里不再介绍。

2 预报模型的建立 2.1 支持向量机算法简介

本文采用支持向量机的两种变形形式——线性规划支持向量机(LP_SVM)和最小二乘支持向量机(LS_SVM)^[10]。考虑到便于拓展的需要，算法均由FORTRAN语言实现。

支持向量机算法实现的过程中，核函数较为重要，核函数具体实现了空间变换，使数据空间的维数得到改变，解决了非线性问题。可以这样说，核函数为线性时，相应的支持向量机也为线性的，反之，为非线性的。常见的核函数主要有4种。

(1) 线性核函数K(x, x′)=(x·x′)

(2) 多项式核函数K(x, x′)=(x·x′)^d

(3) 径向基核函数K(x, x′)=exp(-γ‖x-x′‖²)

(4) Sigmoid核函数K(x, x′)=tanh[s(x·x′)+c]

以上核函数中的d、γ、s和c均为参数，在算法的具体实现中需要借用K-折交叉确认(K-fold cross-validation)的思想逐个循环进行核函数的确定和最优核参数的选择。

(1) LP_SVM是基于C支持向量机的原问题和对偶问题的变形而得到的，其形式为：

$\begin{align} \max\limits_{\alpha ,b,\beta}&-lC-\sum\limits_{i=1}^{l}{{{\alpha }_{i}}}+C\sum\limits_{i=1}^{l}{{{y}_{i}}}[\sum\limits_{j=1}^{l}{{{\alpha }_{j}}{{y}_{j}}K({{x}_{j}},{{x}_{i}})}]+ \\ &Cb\sum\limits_{i=1}^{l}{{{y}_{i}}-C\sum\limits_{i=1}^{l}{{{\beta }_{i}}}} \\ st\ \ \xi &=1-{{y}_{i}}(\sum\limits_{j=1}^{l}{{{\alpha }_{j}}{{y}_{j}}K({{x}_{j}},{{x}_{i}})}+b)+{{\beta }_{i}} \\ &i=1,\cdots ,l \\ {{\alpha }_{i}},&{{\beta }_{i}},{{\xi }_{i}}\ge 0~~~~i=1,\cdots ,l \\ \end{align}$

对于线性规划问题这里采用能够克服退化和无限循环的基于Bland规则的单纯形算法(Simplex Method)方法^[12]解决。

(2) LS_SVM由Suykens在1999年提出，其形式：

$\begin{align} &\left(\begin{matrix} \mathit{\boldsymbol{\varOmega}}\text{ }&Y \\ {{Y}^{T}}&0 \\ \end{matrix}\right)\left(\begin{matrix} \mathit{\boldsymbol{\alpha}}\text{ } \\ b \\ \end{matrix}\right)=\left(\begin{matrix} \mathit{\boldsymbol{I}} \\ 0 \\ \end{matrix} \right) \end{align}$

其中 ${{\mathit{\boldsymbol{\varOmega}}\text{ }}_{ij}}={{y}_{i}}{{y}_{j}}K({{x}_{i}},{{x}_{j}})+\frac{{{\delta }_{ij}}}{C}$

由于Ω是对称的半正定矩阵，这里可以利用该矩阵的性质，采用追赶法或平方根方法^[13]进行解决。

最小二乘支持向量机将不等式约束转化为等式约束，失去了支持向量的稀疏性，而最小二乘支持向量机的难点也在于支持向量的稀疏性处理。Suyken等^[14]提出了一种简单易行的剪枝方法进行支持向量的稀疏性处理，即按照一定的步长逐步去掉绝对值较小的Lagrange乘子对应的支持向量。通过试验发现，具体的剪枝阈值根据最小二乘支持向量机的分类效果而定。

两类支持向量机的决策函数均为：

$\begin{align} f(x)=&\text{sgn} [g(x)]= \\ &\text{sgn} \{\sum\limits_{i=1}^{l}{\alpha _{i}^{*}{y}_{i}[{x}_{i} \cdot \varPhi (x)]}+{b}^{*}\} \end{align}$

其中 $x\xrightarrow{\varPhi}\mathit{\boldsymbol{X}}={\varPhi}(x)$ 属于引进核函数时做的空间变换，以应对部分线性不可分情况。

2.2 预报模型建立

释用预报中，一般依据天气型建模或者逐月(季)建模。天气分型主要有两个大的方面，一是主观经验分型；二是客观的环流指标分型以及典型场相似分型^[15]。在预报对象复杂、天气型较难判断或者判断结果不符合实际的情况下，可以建立逐季(月)的释用预报模式^[2]。在本文，采用逐月建模。

这里根据是否采用主成分分析和运用支持向量机模型，共设计6个方案。即仅采用Fisher线性判别的RAW_Fisher，主成分-Fisher判别的PCA_Fisher，仅采用最小二乘支持向量机的RAW_LSSVM，主成分-最小二乘支持向量机的PCA_ LSSVM，仅采用线性规划支持向量机的RAW_LPSVM，主成分-线性规划支持向量机的PCA_ LPSVM。其中这6个方案涉及到3种模型，即Fisher、LS_SVM、LP_SVM。

2.3 预报技巧的评价

目前，天气预报的检验和评估方法较多，雷暴属于小概率事件，本文采用适合小概率事件的临界成功指数CSI(风险评分TS)、Heidke技巧评分HSS和Gilbert技巧评分GSS，这三种评分方法进行预报效果的评估^[16]。

(1) 临界成功指数CSI(critical success index)：临界成功指数又称之为风险评分TS(threat score)，反映了事件“出现且报对”时的预报水平。

(2) Heidke技巧评分HSS(Heidke skill score)，HSS表示实际预报准确率比随机预报准确率到底提高了多少，其值在[-1, +1]之间，HSS>0表示预报水平高于随机预报水平，预报完全正确是HSS=1。

(3) Gilbert技巧评分GSS(Gilbert skill score)，GSS实际上是CSI扣除随机预报正确次数后得到的，因此又称之为技巧临界成功指数，其值在[-1/3, +1]之间，GSS>0表示预报水平高于随机预报水平，预报完全正确是GSS=1。

以上3种预报评分方法可以综合使用，当HSS和GSS均大于零时，CSI越大则预报方法越好；或者CSI无太大差异时，HSS和GSS越大时预报方法越好。

3 个例试验与结果分析

试验站点选为海口站。海口站是雷暴发生的甚高密度区，其一年四季均有雷暴发生，5—8月是雷暴发生的集中期。海口位于琼州海峡南侧附近，受海陆热力影响更多，其雷暴的日分布也有明显的变化。

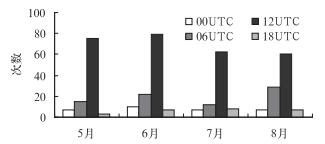
通过统计：海口站2002—2007年5—8月的各月雷暴日天数的分布总体较为平缓；但是雷暴的日分布却有很明显的变化，5—8月各月情况类似，即每天下午到前半夜是雷暴的高发时间段，其他时间段雷暴发生的概率相比显得极小，如图 1。

在采用预报模型预报之前，采用了1个消空因子进行了消空预报。因此对于“消空成功”或者“过消空”的结果都放在预报方程的预报结果中进行统计和最后预报方法的评估。

首先分析不同方案的总体预报效果(表 1)。由结果可知：

(1) 当仅进行因子的初选时，RAW_LSSVM、RAW_LPSVM、RAW_Fisher这3种方案的HSS和GSS评分均大于零，雷暴的预报结果好于随机预报，这说明预报流程的设计是有效果的，整个预报流程是合理的；3种方案中，最小二乘支持向量机的预报效果最好，CSI评分约为0.23，HSS和GSS评分均大于其他两种方案，两种形式支持向量机的预报效果均要好于线性的Fisher判别，因而支持向量机的预报效果要好于线性的Fisher判别预报模型。

(2) 因子的精选涉及到主成分分析时，PCA_LSSVM、PCA_LPSVM、PCA_Fisher 3种方案的HSS、GSS和CSI评分相较于未进行因子精选的预报效果有明显的提高，CSI评分最低的Fisher也达到了0.28，说明在释用预报中减少因子数目、进一步综合因子和进行因子的精选是很有必要的；3种方案中，仍然是最小二乘支持向量机的预报效果最好，其CSI评分达到了近0.40，HSS和GSS评分均大于其他两种方案，两种形式支持向量机预报CSI评分均超过了0.30，进一步说明了支持向量机方法较线性判别方法具有一定的优越性。虽然预报评分有了一定提高，但是这种提高是建立在较大的样本规模基础之上的，即预报时次是那些样本达到一定规模的时次(自行设计的程序中规定样本个数大于50时才进行因子的精选)，所以预报评分在这里仍不能完全说明预报方法的绝对优越性，但是应当注意的是对于样本较少时次的预报应该不要仅仅局限于定量的方法，可以考虑对流参数区域叠套等方法的运用。

由以上分析发现，对于海口站，最小二乘支持向量机是最好的预报形式，进行主成分分析后预报效果有明显提高。因此下面按照样本多时采用PCA_LSSVM，样本少时RAW_LSSVM这种组合方式统计各个时次和各月的预报结果。

先分析各个时次的预报结果，由表 2可知：12和36 h预报效果最好，这两个时次都对应海口当天下午，是海口站雷暴高发时间段；30 h的CSI评分有0.15，这个时间对应海口当天的中午前后，雷暴也经常发生；18和24 h的预报效果虽然HSS和GSS评分均大于零，但是总体都较差，这也与海口站夜间到第二天鲜有雷暴的时间段相对应；此外12和36 h两个预报时刻其实均对应于12 UTC，但是发现36 h的预报CSI评分要高于12 h的，这说明模式的输出存在形势场的过快或者过慢，某些物理场也随着预报时效的增加变得过大或者过小。

由这些分析可以发现，对于雷暴的模式产品释用预报，如果一直运用一种方法和均匀6 h的间隔进行预报，不考虑当地的雷暴的日分布规律，预报效果并不好，这就要求某些时间段可以进行加密预报，某些时间段可以放稀疏些；此外，为了适应样本，预报方法也可以采取灵活的方式，比如一些定性的、非方程形式的方法。

接着分析各月的预报结果，如表 3。由该表可知：6月的预报效果最好，7月预报效果较差；由于逐月建模是分别将各月作为建立不同气候背景的依据，考虑到海口所处的地理位置，其发生雷暴时的环流形势在5—6月都是分别有所侧重的，但是7和8月的环流形势经常被副热带高压、台风和低槽等天气型交替影响，因此预报效果也受到了一定的影响。

4 结论

论文利用2002—2006年AREM模式产品和常规观测报文资料，逐月建立了支持向量机的单站雷暴释用预报模型，并针对海口站2007年5—8月进行了具体的预报，结果表明:

(1) 在不同的预报方案中，支持向量机较线性Fisher判别的预报效果好，其中最小二乘支持向量机的预报效果最好。由此可见，支持向量机结合AREM模式产品进行释用预报是合适的，用支持向量机方法建立预报方程较线性Fisher判别效果优。

(2) 在主成分分析前后，支持向量机和Fisher判别的预报效果均有明显改变，这些说明：对于雷暴这种较为复杂的天气现象的预报，通过一定方法综合和精简其预报因子，会对最终的预报结果起到积极的作用。

(3) 通过对各个时次和各月的预报结果分析发现：雷暴的预报效果在雷暴活跃期较好，而在雷暴的沉寂期却相对较差，这些结果一方面说明了预报方程的预报效果与样本的规模有关，另一方面也说明了对雷暴沉寂期缺乏细致的研究，规律难觅，预报仍较难。