引言

太阳辐射是地球大气运动的最主要能源，是气候形成和演变过程中重要的外参数^[1]，也是生态系统过程模型、水文模拟模型和生物物理模型研究中的重要输入参数^[2-5]。太阳辐射通过大气时，要受到空气分子(CO₂、O₃、O₂等)、水汽以及气溶胶质粒的吸收和散射而减弱^[6]。由于大气中水汽和气溶胶含量的不确定性，因此，要准确描述辐射过程是比较困难的。

近年来，大规模太阳能发电已成为国际上应对气候变化、调整能源结构的重要举措。高精度太阳能资源计算是太阳能资源评估的基础。同时，随着大规模集中并网光伏发电系统容量的增加，为了避免发电系统输出功率固有的间歇性和不可控等缺点对电网的冲击，有效减轻太阳能并网发电对电网的影响，开展了太阳能发电量预报技术研究。逐时、逐日等高时空分辨率的太阳能资源量计算和预测是太阳能发电量预报的基础。在太阳能资源计算中，起始辐射数据是影响计算精度的重要基础数据，选择一个好的起始数据，对提高计算精度具有非常重要的意义。目前，大多采用天文辐射作为起始数据。由于我国地域广阔，海拔高度变化大(天顶角范围变化大、海拔高度差大)等原因，海拔高度对太阳辐射的影响天文辐射是无法考虑的。因此，王炳忠等^[7]也提出利用理想大气辐射量作为计算太阳能资源的基础辐射量。理想大气(指不含水汽和气溶胶的干洁大气)对太阳辐射的影响(主要受到空气分子Rayleigh散射、O₃以及其他气体分子的选择吸收)是可以获得的。因此，理想大气太阳辐射成为高时空分辨率太阳辐射计算的重要起始数据，理想大气太阳辐射计算的准确与否直接影响着太阳辐射估算的精度。最早由Moon 1940年^[8]提出的太阳辐射机理模型使得太阳辐射模型由统计模式向大气传输的物理过程模式发展。1975年McMaster University的Davies等提出的MAC模型^[9-10]是太阳辐射机理模型的代表。在近几十年，太阳辐射机理模型的研究得到了广泛的发展和应用。比较有影响的是：得到广泛应用的Bird Clear Sky Model^[11]、Iqbal Model C^[12]、被用于美国国家太阳辐射数据库建设的METSTAT Model^[13]，以及广泛应用于工程与建筑业的ASHRAE Model^[14]、用于制作《欧洲太阳辐射图集》的Page Model^[15]、多层透射率的MLWT2^[16-17]等模型。最复杂的太阳辐射模型是以LOWTRAN^[18]和MODTRAN^[19]为代表的频谱模型。Gueymard^{[17, 20]}曾对许多宽光谱太阳辐射模型的直接辐射模型进行理论、实验数据检验，结果表明许多模型由于不正确的透射率方程或者简单的假设造成模型缺陷或严重的局限性。这表明太阳辐射模型还有改进的空间。

本文在对宽广谱模型与精确的谱模型比较的基础上，提出一个修正的理想大气太阳辐射模型。

1 理想大气太阳辐射模型 1.1 宽光谱模型

宽光谱的大气辐射模型是指：研究对象为直接太阳光，它包含了波长为0.2~4 μm的波动，通常考虑的是整层大气，即将大气看成一层(Broadband)。经过大量模型的初步筛选，选取了几个应用广泛、国外公认并且其主要的大气消减过程都有单独的透射率公式的宽光谱太阳辐射机理模型：Iqbal Model C^[12]、METSTAT^[13]、MMAC^[9-10]、MLWT2^[17]、Perrin^[21]、REST^[17]和Yang等^[22]模型。表 1是所选取的太阳辐射模型的结构，其详细的模型描述可参阅参考文献，这里不再分别给出。

在晴空条件下METSTAT模型基本上与Iqbal Model C是一致的。Rayleigh分子散射、O₃吸收、均一混合气体吸收的透射率计算公式没变。标准大气压下的空气质量M_r据Kasten等^[23]公式计算。经过严格的理论和观测数据检验，该模型具有较高精确度，属于Gueymard推荐的7个模型之一。因此，这里仅研究METSTAT模式。

在理想大气下，将各模型的大气透射率(T_R为空气分子Rayleigh散射；T_O为O₃的吸收；T_UM为均一混合气体的吸收)和直接辐射计算结果与基于MODTRAN基础上发展的、精确的谱模型SMARTS^[24-25]计算结果逐一进行严格的比较。据比较，SMARTS2和MODTRAN取得很好的一致性：在天顶角Z<66.5°范围内，误差小于1%。

所有的比较均以美国标准大气(U.S. Standard Atmosphere，USSA)作为参考大气，海拔高度分别取0、1、2、3和4 km 5个高度、天顶角的计算范围为0~87°。

在计算O₃的厚度时，为了更准确，引进订正系数C_t：

${U_O}{\rm{ = 0}}{\rm{.3438}}{C_t}$

(1)

${C_t}{\rm{ = }}\,\,\,{\rm{1}} - {\rm{0}}{\rm{.00898}}H$

(2)

式中，H为海拔高度(km)；U_O为O₃厚度(atm-cm)。

1.2 谱模型SMARTS

SMARTS是太阳大气辐射传输光谱模型(即Simple Model for Atmospheric Transfer of Sunshine), 它涵盖了具有不同波长间隔的全部太阳光谱区域(280~4000 nm)，其中280~400 nm间的波长间隔为0.5 nm，400~1700 nm间的波长间隔为1 nm，1705~4000 nm间的波长间隔为5 nm。各透射率、直射太阳辐射、散射辐射和总辐射由SMARTS代码计算获得(SMARTS 2.9.5，简称SMARTS2)。SMARTS代码可以选取10种不同的理想大气状况，本文选用其中的一个典型大气状况——标准美国大气状况。

1.3 模型性能评价指标

模型的性能评价指标包括：

均方差(Root Mean Square Error，RMSE)表明误差的离散程度。

$RMSE{\rm{ = }}\sqrt {[\sum\limits_{i = 1}^n {{{({k_i} - {{\widehat k}_i})}^2}/n} ]} $

(3)

平均绝对误差(Mean Absolute Error，MAE)

$MAE{\rm{ = }}\frac{1}{n}\sum\limits_{i = 1}^n {\left| {({k_i} - {{\widehat k}_i})} \right|} $

(4)

平均相对误差绝对值(Mean Absolute Percentage Error, MAPE)：表明估算相对误差的平均状况。

$MAPE{\rm{ = }}\frac{1}{n}\sum\limits_{i = 1}^n {\left| {(\frac{{{k_i} - {{\widehat k}_i}}}{{{k_i}}})} \right|} $

(5)

式中，k_i、 ${\hat k_i}$ 分别为SMARTS2模型计算的参考值和其他模型的预测值。

2 模式比较 2.1 相对光学质量的比较

当考虑大气内发生的吸收和散射时，必须要知道辐射所通过的吸收和散射物质的总质量，这就是光学质量。在天顶角较大时，由于大气曲率和空气密度随高度的变化所引起的大气折射的影响就变得极为重要了。通常，相对光学质量都是采用近似的经验公式计算。因此，相对光学质量计算公式的精确与否，直接关系到太阳辐射模型的准确度。

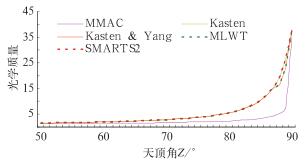
上述模型中涉及到的相对光学质量公式有：MMAC、Kasten^[26]、Kasten & Yang和MLWT2，将其分别和SMARTS模型中的相对光学质量公式计算结果比较(图 1)。结果表明：当天顶角Z>30°时MMAC模型中相对光学质量计算有较大的误差(图略)，Kasten和Kasten & Yang的相对光学质量在Z>80°时稍有误差，MLWT、Kasten & Yang和SMARTS2吻合得较好(REST采用的是SMARTS中的相对光学质量公式)，具有较高的精确度。

2.2 模型大气透射率的比较 2.2.1 空气分子Rayleigh散射的透射率T_R

大多数太阳辐射模型单独考虑空气分子Rayleigh散射透射率(T_R)，但MLWT2将其和均一混合气体透射率T_UM结合起来计算的。

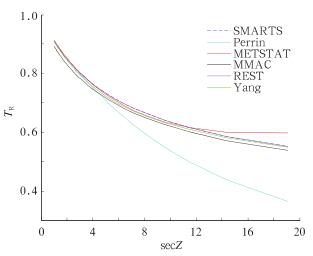
图 2和表 2是所选取模型中单独考虑T_R和谱模型SMARTS2计算的T_R进行比较的结果。表明：这几个模型T_R计算精度都较高，其MAE小于0.05，除MMAC模型外，MAPE均小于5%，以METSTAT模型精度最高，其次是REST、Yang等模型。MMAC的误差最大，Perrin次之。它们对T_R估算严重低估，这主要是由于模型的局限性造成的，MMAC的相对光学质量公式误差较大也是原因之一。

在天顶角Z>85°时METSTAT对T_R的估算偏大，这主要是由于该模型低估了Rayleigh散射对太阳短波辐射的影响，随着天顶角的增大误差也增大。

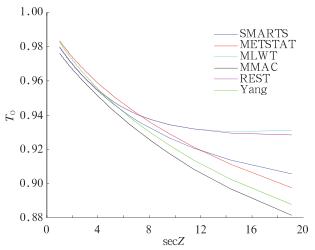
2.2.2 O₃分子透射率

Perrin模型是将T_O和T_UM结合在一起考虑的，没有单独的T_O公式。表 3和图 3是所选取模型中考虑臭氧吸收的透射率T_O和谱模型SMARTS2计算的T_O进行比较的结果，各模型结果和SMARTS2的吻合较好，精确度都较高。以REST和MLWT2模型的预测精度最高，其次为Yang和METSTAT。

从图 3中也发现：当M_r>5.0(即天顶角Z>80°)时，各模型与SMARTS的T_O误差开始偏大。随着M_r的增大，误差也增大。这主要是由于大多数模型在计算T_O时臭氧的相对光学质量(M_O)采用空气的相对光学质量M_r来代替的。事实上，臭氧相对光学质量M_O比空气光学质量(M_r)要小，尤其在天顶角较大时，它们之间的差异更大，例如，在天顶角Z=90°时，M_O=16.601，而M_r=38.136。这是影响模型精确度的一个主要原因。

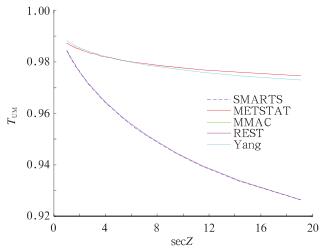
2.2.3 均一混合气体吸收的透射率T_UM

表 4和图 4是具有中T_UM和SMARTS2进行比较。MMAC模型的T_UM固定为1，MMAC计算精度最差。除了REST模型和SMARTS吻合得很好，精度较高，其余模型的RMSE均大于0.01。METSTAT、Yang等模型由于主要考虑O₂和CO₂气体对短波辐射的吸收，而REST充分考虑了CO₂、O₂、CH₄、CO、N₂和N₂O等多种气体的吸收，因此其T_UM较其他模型有所减小，反映出均一混合气体对太阳短波辐射的影响增大。

3 理想大气太阳辐射模型修正模型 3.1 大气透射率的修正

根据上述理想大气下宽光谱太阳辐射模型的透射率比较，可以看出REST模型的透射率精确度最高，预测效果最好。但是，由于它的透射率公式是对谱模型透射率的拟合，此模型的作者认为由于受比尔-布格-朗伯定律的限制，当将其外推到宽光谱模型计算时，不能保证总是很好^[19]。所以选取应用广泛的、大气透射率精确度也很高的宽光谱模型METSTAT对其大气透射率进行改进。

模型修正是基于以下几点考虑：

(1) 相对光学质量的修正。虽然METSTAT模型中采用的相对光学质量的计算公式和SMARTS的计算结果较一致，但在天顶角较大时仍略有偏差，因此，我们采用谱模型SMARTS中的相对光学质量，进一步提高模型的计算精度。

(2) 臭氧吸收透射率的改进。在METSTAT模型中，计算T_O采用空气相对光学质量替代臭氧的相对光学质量，由于在天顶角较大时，臭氧的相对光学质量远远小于空气的相对光学质量，是影响T_O精度的主要原因。因此，在改进的模型中，T_O采用SMARTS模型中臭氧的相对光学质量^[22]计算，减小模型的计算误差。

(3) 均一混合气体的吸收透射率的改进。由于METSTAT模型仅考虑了CO₂和O₂气体对太阳辐射的吸收。随着对太阳辐射的进一步认识，基于最新的气体吸收谱线资料，均一混合气体仅考虑CO₂和O₂对太阳辐射吸收的影响，是远远不够的。因此，在修正的模型中将采用REST模型考虑多种气体的吸收对太阳辐射的影响。

下面是修正的模型METSTAT_M大气透射率公式：

${T_R}{\rm{ = }}{{\rm{e}}^{ - {\rm{0}}{\rm{.0903}}M_a^{{\rm{0}}{\rm{.84}}}}}{\rm{(1 + }}{M_a} - M_a^{^{{\rm{1}}{\rm{.01}}}}{\rm{)}}$

(6)

$\begin{array}{l} {T_O}{\rm{ = 1}} - {\rm{0}}{\rm{.1611}}{X_O}{{\rm{(1 + 139}}{\rm{.48}}{X_O}{\rm{)}}^{ - {\rm{0}}{\rm{.3035}}}} - \\ {\rm{0}}{\rm{.002715}}{X_O}{\rm{(1 + 0}}{\rm{.044}}{X_O}{\rm{ + 0}}{\rm{.0003}}X_O^{\rm{2}}{\rm{)}} - {\rm{1}} \end{array}$

(7)

${T_{UM}} = {{\rm{e}}^{ - 0.0127M_a^{0.26}}}$

(8)

其中

${M_a} = {M_r}\left( {\frac{p}{{{\rm{1013}}{\rm{.25}}}}} \right)$

(9)

${M_o} = {[\cos Z + 1.065{Z^{0.6379}}/{(101.8 - Z)^{2.2694}}]^{ - 1}}$

(10)

${X_O} = {U_O}{M_O}$

(11)

式中，X_O为订正后的臭氧厚度，单位(cm)，U_O用公式(1)。M_r见文献[22]。M_a是无量纲，为经气压订正后的空气质量。表 5是METSTAT_M与SMARTS模型透射率的比较。结合前面表 2到表 4，将METSTAT_M和METSTAT模型的计算的大气透射率比较，结果表明METSTAT_M的大气透射率无论是在RMSE还是MAE上比METSTAT模型都有不同程度的提高，T_R、T_UM和T_O的计算误差MAPE分别较原模型的3.2%、0.41%和0.95%提高到2.98%、0.34%和0.17%，明显优于原来的模型。可见，METSTAT_M模型精度是最高的，且形式比Yang、REST等模型简单，便于网格点上的海量数据的计算。

3.2 理想大气下直接辐射的比较

理想大气下总辐射：

${E_t} = {E_b} + {E_d}$

(12)

${E_b} = {E_0}{T_R}{T_O}{T_{UM}}$

(13)

${E_d} = {D_r} + {D_m}$

(14)

${D_r} = \frac{{0.79{E_0}\cos Z{T_O}{T_{UM}}0.5(1 - {T_R})}}{{(1 - {M_a} + M_{_a}^{1.02})}}$

(15)

${D_m} = \frac{{({I_n}\sin {h_\theta } + {D_r}){\rho _g}}}{{1 - {\rho _g}}}$

(16)

式中，E_t、E_b和E_d分别为理想大气总辐射、直接辐射和散射辐射；D_r为空气分子Rayleigh散射；D_m为地表与大气间的多重散射；h_θ为太阳高度角；ρ_g为地表反射率。大气透射率T_R、T_UM和T_O应用修正的模型。

在理想大气下，根据各模型计算的直接辐射和SMARTS的计算结果进行比较(表 6)，结果表明：除了REST模型外，METSTAT_M模型的计算精度是最高的，比改进前的METSTAT模型精度平均提高了近50%。

将改进的散射辐射模型METSTAT_M和METSTAT进行比较(表略)，MAPE由7.51%提高到6.42%，均方根误差(RMSE)为3.33。

将改进模型与原模型的总辐射与SMARTS计算结果比较，METSTAT_M经计算，平均相对误差(MAPE)为0.65%，均方根误差(RMSE)为8.21，而METSTAT的平均相对误差为1.07%，均方根误差(RMSE)为12.84，改进后的模型METSTAT_M精度提高了许多。

4 讨论

本文选取多个国外应用广泛、得到公认并且其主要的大气消减过程都有单独的透射率公式的宽广谱太阳辐射机理模型，在理想大气下将各模型的透射率(T_R、T_O和T_UM)以及直接辐射、散射辐射与精确的谱模型SMARTS逐一进行严格的比较；并在此基础上选取模型精确度较高的METSTAT模型，对模型中的相对光学质量、臭氧吸收透射率、均一混合气体吸收透射率等存在的缺陷和不足进行修正后，获得一个改进的理想大气太阳辐射模型METSTAT_M。通过研究表明：

(1) 从相对光学质量比较结果来看，当Z>30°时MMAC模型中相对光学质量计算有较大的误差，Kasten、Kasten & Yang的相对光学质量在Z>80°时稍有误差，总体是MLWT、Kasten & Yang和SMARTS2吻合的较好，具有较高的精确度。

(2) 从大气透射率比较结果来看，所选模型的T_R计算精度都较高，以REST模型的精度最高；所选模型的T_O计算结果和SMARTS2的吻合较好，尤以REST和MLWT2模型的预测精度最高；T_UM计算结果以REST精度最好。

(3) 改进的理想大气太阳辐射模型METSTAT_M的大气透射率无论是在RMSE还是MAPE上比METSTAT模型都有不同程度的提高，T_R、T_UM和T_O的MAPE结果分别较原模型的3.2%、0.41%和0.95%提高到2.98%、0.34%和0.17%。

(4) 改进的理想大气太阳辐射模型METSTAT_M的直接辐射计算结果平均相对误差由0.92%提高到0.48%，散射辐射由7.51%提高到6.42%，总辐射由1.07%提高到0.65%，改进以后的模型精度提高了许多。

上述研究结果表明METSTAT_M模型具很高的精确度，并且模型形式简单，便于计算，优于其他的模型。