2. 中国气象科学研究院,灾害天气国家重点实验室,北京 100081
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
多普勒天气雷达不仅能实时监测各种强对流天气,还可以定量地估测探测范围内的降水。但由于雷达探测不是直接对降水本身的测量,因此不可避免地易受到雷达探测高度、降水类型等许多因素的影响,使得雷达估计值和降水实况之间存在偏差。雨量计是测量降水最直接有效的工具, 使用雨量计可以实现对地面单点降水的精确测量,但其测量结果往往因站网密度有限而缺乏代表性。随着自动化探测技术的不断提高,自动站在许多国家得到迅速发展,国内各地也相继建立起加密自动站网, 这为实时监测天气特别是中小尺度强对流天气以及开展雷达-雨量计联合校准雷达估测降水的分析研究提供依据和资料支持。但如何将雨量计对单点的准确测量和雷达测量降水的高时、空分布优势相结合, 校准雷达, 提高雷达定量估测降水的精度,长期以来一直是雷达气象和水文专家们研究的重点和难点。
雷达-雨量计联合校准常用的校准方法有Z-I关系法[1-3]、最优插值法[4]、卡尔曼滤波校准法[5-6]、变分校准法[7]、Kriging法[8]、概率配对法[9]等。但其校准前提是地面要有一定分布密度的雨量计网,以达到尽可能缩小雷达和雨量计在雨量站点上存在测量偏差的目的。Wilson[10]通过采用雨量计和雷达测量降水的比值校准降水估计,证实一部雨量计可以改善雷达在1000平方英里(1英里=1.6093 km)区域内对降水的测量,使其均方根误差减小39%。Brandes[11]研究了基于雨量计单点校准雷达估测降水的空间变化。随后Koistinen等[12]对Brandes提出的方法进行了改进,但当加入距离因子时涉及的雨量计网观测密度变化和Brandes所得结论是一致的。Herndon等[13]使用老式雷达系统对对流性降水过程进行的研究表明,当考虑所使用的雷达系统和试验区域的地理位置时,对1小时降水使用布设在1000 km2内的17部雨量计得到的降水精度与雷达估测降水场相当。Harrold等[14]分析了不同区域范围内与雨量计相对应的雷达测量的误差特征,用以研究在相对近距离范围内雷达测量所需要的校准雨量计密度。Woodley等[15]对美国南部不同流域面积内发生对流性降水时的雨量计密度进行了研究分析,指出在570 km2的加密实验区域内需要的校准雨量计密度为26 km2·部-1;当研究区域扩大至13000 km2的试验区域时,所需雨量计密度也只是143 km2·部-1即可。
中国基于雷达和雨量计的降水估计研究也较多[16-27],其中张培昌等[17]用变分法把各雨量计资料内插到所选区域的各个网格点上,得到降水量“真值场”;李建通等[19-20]将最优插值法引入校准领域,并在最优插值法和卡尔曼滤波法的基础上提出了分步校准法;黄小玉等[21]将漂移克里金方法应用到雷达-雨量计联合估测降水中。本文采用黄淮项目雷达估测降水算法软件中的变分校准技术方法,选取不同类型降水过程,以校准区域内所有雨量计校准雷达得到的估测降水场作为“真值场”,对比分析14种不同密度雨量计网校准雷达估测降水的效果,并对雨量计网中单个站点对校准的贡献进行试验分析研究,以探讨不同降水类型下校准雷达需要的雨量计密度及雨量计网中单个站点对校准的贡献,为更好地开展联合雨量计校准雷达估测降水的研究及科学合理布设地面自动站提供有用的参考依据。
1 校准方法和雨量计分布密度 1.1 校准方法和资料校准方法采用黄淮项目雷达估测降水算法软件中的变分校准技术方法,这种校准方法的基本思想是[22]:将同时有雷达回波和雨量计值的点k(k=1,2,…,n)上的实测校准因子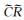
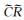
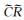
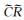
| $\sum\limits_i {} \sum\limits_j {{{[CR(i,j) - \widetilde C\widetilde R(i,j)]}^2}} \to \min $ | (1) |
可以看出,变分校准法的优点是明显的,无论是Z-I关系和雷达参数不稳,或者距离变大、降水粒子非球形以及雨区衰减等带来的影响,均可因使用CR(i,j)场进行逐点校正而得到一定的订正,使测雨精度大大提高。但变分校准法要求地面上有一定分布密度的雨量计网,以保证有一部分质量好的值可以作为校准值用。天津地区雨量计网由232个自动气象站组成,雨量计平均站距不足8 km,分布密度约为19.7×10-3·km-1,符合变分校准法的要求。
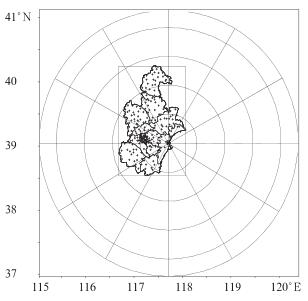
所用雷达资料采用天津新一代天气雷达基数据资料,所用资料经过去除地物杂波和超折射回波等非气象杂波的质量控制[28-29];雨量计资料选用天津自动雨量计站点资料,使用时去除因仪器故障等原因造成雨量计数据不可用的站点资料(图 1为天津雷达和地面自动雨量计的分布)。进行校准的降水个例选取代表三种不同类型降水的天气过程,分别为:2008年6月27日积云强对流天气过程、2008年7月14日积层混合云对流性降水过程和2009年4月19日层云稳定性降水过程。
|
图 1 天津地面自动站分布 (中心为雷达位置,圈距50 km,+代表地面雨量计;方框范围为校准试验区域) Fig. 1 Tianjin radar and raingauge distribution (Center is the radar located, lap distance 50 km, '+'showing raingauge; box range showing the calibration test area) |
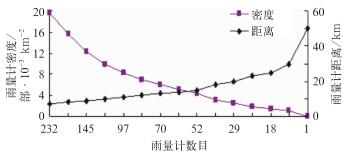
校准雨量计站点的选取原则为在相同区域内雨量计的分布相对均匀,随机选取雨量计,通过不断减小校准站点之间的距离,达到校准雷达雨量计网密度逐步加大的目的。本文共选定14种不同密度分布的校准雨量计网(图 2)。考虑到自动雨量站实际分布的不均匀性,文中所给雨量计站距为近似值。
|
图 2 校准网中雨量计分布密度与雨量计站点间距离对应图 (站距=50,表示全区只有一个雨量计参加校准) Fig. 2 The comparison map of raingauge site distance and density (The distance=50, indicating only one raingauge calibration) |
校准时采用的降水Z-I关系为Z=300×I1.4,时间步长为1小时。校准范围为所有雨量计参加校准的区域(图 1中方框选定的区域),从图上看到,所选校准区域在雷达140 km探测范围内,这样在校准时距离折叠对雷达估测降水效果的影响可以忽略不计。假定所有雨量计参加校准时的雨量计网为“最大密度雨量计网”、用其校准雷达得到的估测降水场为“真值场”。校准场格点分辨率1 km×1 km,校准区域范围共有119×191个格点数据。
1.3 校准效果的评估检验指标采用比率(Ra,也称偏差)、均方根误差(Rm)和相关系数(C)作为校准评估检验指标。比率、均方根误差、相关系数的计算公式分别如下:
| ${R_a} = \frac{{\sum\limits_{j = 1}^M {} \sum\limits_{i = 1}^N {{G_{ij}}} }}{{\sum\limits_{j = 1}^M {} \sum\limits_{i = 1}^N {{R_{ij}}} }}$ | (2) |
| ${R_m} = \sqrt {\frac{{\sum\limits_{j = 1}^M {} \sum\limits_{i = 1}^N {{{({G_{ij}} - {R_{ij}})}^2}} }}{{MN}}} $ | (3) |
| $C = \frac{{\sum\limits_{j = 1}^M {\sum\limits_{i = 1}^N {({R_{ij}} - \overline R )({G_{ij}} - \overline G )} } }}{{\sqrt {\sum\limits_{j = 1}^M {\sum\limits_{i = 1}^N {{{({R_{ij}} - \overline R )}^2}} } } \sqrt {\sum\limits_{j = 1}^M {\sum\limits_{i = 1}^N {({G_{ij}} - \overline G )}^2 } } }}$ | (4) |
式中G为以所有有效雨量计参加校准得到的估测降水场格点降水量“真值”,R是雷达估测的格点降水量,i为第i个时次,j为第j个格点,和分别为“真值”和估测降水量序列的均值,N为降水持续时间(1 h),M为校准区域内格点总数。根据定义,Ra大于和小于1.0,分别表示雷达估测降水相对“真值”的偏低估计和偏高估计,Rm表示雷达估测降水量相对于真值的离散程度,值越小表明离散程度越小,C值越接近1.0,表示雷达估测降水量值同真值序列的相关性越高。
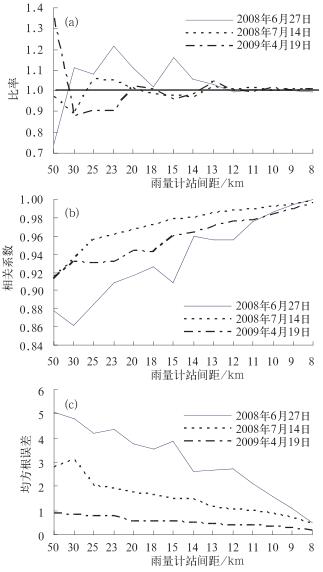
2 不同密度雨量计校准雷达估测降水效果的分析 2.1 不同密度雨量计校准雷达估测降水效果分析对于三次降水过程,当参加校准的雨量计网密度较小时,雷达估测降水的偏差明显(比率值明显大于或小于1),出现弱降水偏高估计、强降水偏低估计的现象;且均方根误差较大、相关系数也不高。随着校准雨量计密度的不断加大,雷达估测降水的偏差逐渐减小、均方根误差迅速减小、相关系数呈线性增大(图 3)。当校准雷达的雨量计网达到一定密度后,雷达估测降水的偏差趋于为零(Ra≈1)、均方根误差达到最小、相关系数达到0.98以上;之后再不断增大校准雨量计的密度,雷达估测降水的效果均没有进一步明显改善。
|
图 3 2008年6月27日、2008年7月14日和2009年4月19日降水过程指标随校准雨量计密度的变化 (横坐标为雨量计站距,代表不同雨量计密度,其中‘50’代表全区只有一部雨量计参加校准) Fig. 3 Performance measures for raingauge calibration density on June 27, 2008 (solid) July 14, 2008 (dashed) and April 19, 2009 (dot-dashed) (Abscisso shows raingauge site distance, representing the different raingauge density>50, showing only one raingauge calibration) |
对于2008年6月27日积云强降水过程,当参加校准的雨量计密度较小时,雷达对降水的低估明显,估测偏差最大达21.7%。但随校准雨量计密度的加大、雷达估测降水偏差与、均方根误差减小、相关系数加大;当校准的雨量计网密度为196 km2·部-1(雨量计站距为14 km)时,校准雷达的估测偏差减小为5%左右、均方根误差为2.6 mm、相关系数达到0.96;之后随校准雨量计网密度的继续加大,检验指标仍有改善。当校准雨量计网密度为121 km2·部-1以上时,雷达估测降水的效果与“真值场”的相当,雷达估测偏差为零、均方根误差达最小、相关系数达0.98以上。之后再不断增大校准雨量计网的密度,雷达估测降水的效果均没有进一步明显改善。所以可以将121 km2·部-1(天津范围需布设97部雨量计)作为这次降水过程校准雷达的最佳密度雨量计网。
对于2008年7月14日降水过程,参加校准的雨量计密度较小时,雷达对降水的估测偏差最大为11.6%;随校准雨量计密度的加大,均方根误差明显减小、相关系数不断加大、比率逐渐趋近于1。当雨量计密度为226 km2·部-1(雨量计站距为15 km)时,校准雷达估测降水的估测误差仅为2%、均方根误差为1.5 mm左右、相关系数达0.98;当雨量计密度为145 km2·部-1时,雷达估测降水的效果与“真值场”的相当,即估测偏差为零,相关系数达到1.0;之后再不断增大校准雨量计网的密度,雷达估测降水的效果均没有进一步明显改善。所以可以将145 km2·部-1(天津范围需布设81部雨量计)作为这次降水过程校准雷达的最佳密度雨量计网。
对于2009年4月19日降水过程,参加校准的雨量计密度较小时,雷达对降水的偏高估测偏差最大为12.1%;随校准雨量计密度的加大、雷达估测精度明显提高,当校准雷达的雨量计密度为405 km2·部-1(雨量计站距为20 km)时,能使雷达对降水的估测偏差降低到1.7%;当雨量计密度为121 km2·部-1时,雷达估测降水的效果与“真值场”的相当,即估测误差为零,均方根误差小于0.37 mm,相关系数达到0.98;之后再不断增大校准雨量计网的密度,雷达估测降水的效果均没有进一步明显改善。所以可以将121 km2·部-1雨量计(天津范围共布设97部雨量计)作为这次降水过程校准雷达的最佳密度雨量计网。
2.2 不同类型降水天气的校准效果对比从图 3和上面的分析看到,校准三次降水过程需要的雨量计密度不同,当校准雷达的估测误差较小时(5%以内),2008年6月27日积云强降水过程需要的雨量计密度为196 km2·部-1、2008年7月14日积层混合云降水过程需要的雨量计密度要小一些,为226 km2·部-1、2009年4月19日层云稳定性降水过程需要的雨量计密度最小,仅为405 km2·部-1。而且校准三次降水过程使雷达估测降水效果与“真值场”的相当时所需的雨量计密度也略有不同,校准2008年6月27日和2009年4月19日降水过程需要的雨量计网密度为121 km2·部-1、校准2008年7月14日降水过程的为145 km2·部-1。这之后对三次降水过程再如何增加雨量计网密度,雷达估测降水的效果均没有进一步明显改善(图 3)。这说明对不同类型降水过程而言,校准雷达的雨量计网密度不一定很大,而是要有一个最佳密度分布的雨量计网,这从一定角度上可为科学合理布设地面自动雨量计网提供参考依据。
3 雨量计校准网中单个站点对雷达估测降水效果的贡献通过分析知,仪器故障或人为因素是造成雨量计测量误差较大的主要原因,所以下面我们通过在校准雨量计网中任意增减雨量计站点和任意改变其中单个站点的降水量值,来分析在校准雨量计网中单个站点对校准雷达估测降水的贡献。下面以2008年7月14日和2009年4月19日两次降水过程为例进行校准试验分析。
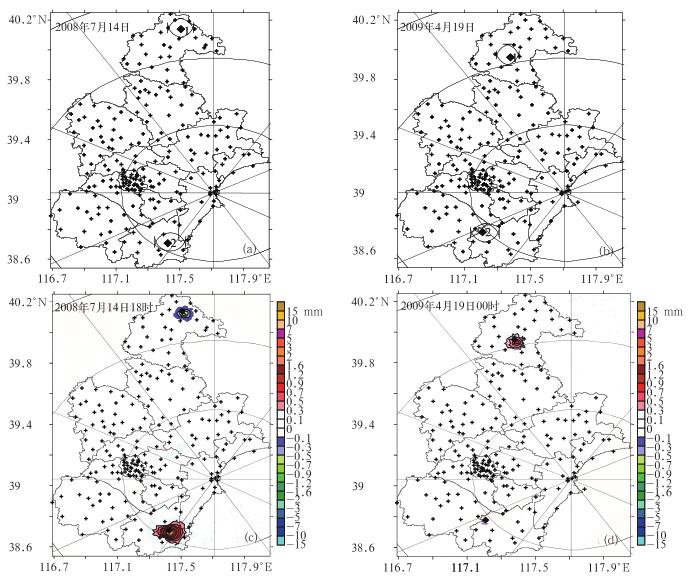
3.1 在校准网中增加雨量计站点在所有雨量计参加校准的“最大密度雨量计网”中任意选取两个降水量为零的站点,采取替换的方式,分别用与其距离最近站点的降水量值代替其的零值(图 4a、4b),然后重新校准雷达,将结果与“真值场”进行对比看到:对两次降水过程,所选站点周围均出现了绝对误差正值或负值区,也就是说增加的站点对估测降水场产生了影响,即在站点周围出现了高估或低估区(图 4c、4d)。从图上看到,任意增加的站点周围出现的高估或低估区的影响范围和站点周围雨量计密度的大小有关,站点1周围雨量计密度大,所以其周围出现估测偏差的影响范围小、而站点2周围的雨量计密度小,所以其周围出现估测偏差的影响范围大。
表 1给出了不同时刻站点1、2的降水量及相对“真值场”的估测绝对误差极值,从表 1看到,增加的站点对校准雷达的贡献是高估或低估?和增加站点本身降水量值的大小无关, 却和站点降水量相对于其周围雨量计降水量平均值的大小有关,当站点的降水量值大于周围站点的平均值时,在站点周围出现高估区;反之在站点周围出现低估区。如2008年7月14日18:00站点1的替换值为4.2 mm、周围雨量计(图 4a站点周围黑圈所示)的平均值为5.6 mm、站点的值小于其周围雨量计的平均值,所以站点1在此时对估测降水场的贡献为偏低估计;而站点2的替换值为10.6 mm、其周围雨量计的平均值为8.8 mm,站点的值大于周围雨量计的平均值,所以站点2在18:00对估测场的贡献为偏高估计(图 4c)。统计表明,这两次降水过程增加的四个站点,在各时次对估测场的贡献符合上述规律的次数占总次数的72%(2009年4月19日04:00—06:00站点1的替换值为零,对校准结果没有影响,统计时去掉了这三个时次)。
|
图 4 (a)、(b)所示为增加的雨量计站点的位置,1、2表示不同站点,圆圈所示为站点周围雨量计的分布;(c)、(d)分别为2008年7月14日18:00和2009年4月19日00:00估测场的绝对误差分布 Fig. 4 Showing the location of the increased raingauge (a, b), (numbers 1, 2 indicate the different sites, the circle shows the distribution around the raingauge site) and the absolute error distributions of radar rainfall estimation at 18:00 UTC July 14, 2008 (c) and 00:00 UTC April 19, 2009 (d) |
|
|
表 1 不同时刻所选站点降水量及相对“真值场”的估测绝对误差极值 Table 1 The variation of the selected raingauge precipitation and the relatively maximum absolute error of radar rainfall estimation |
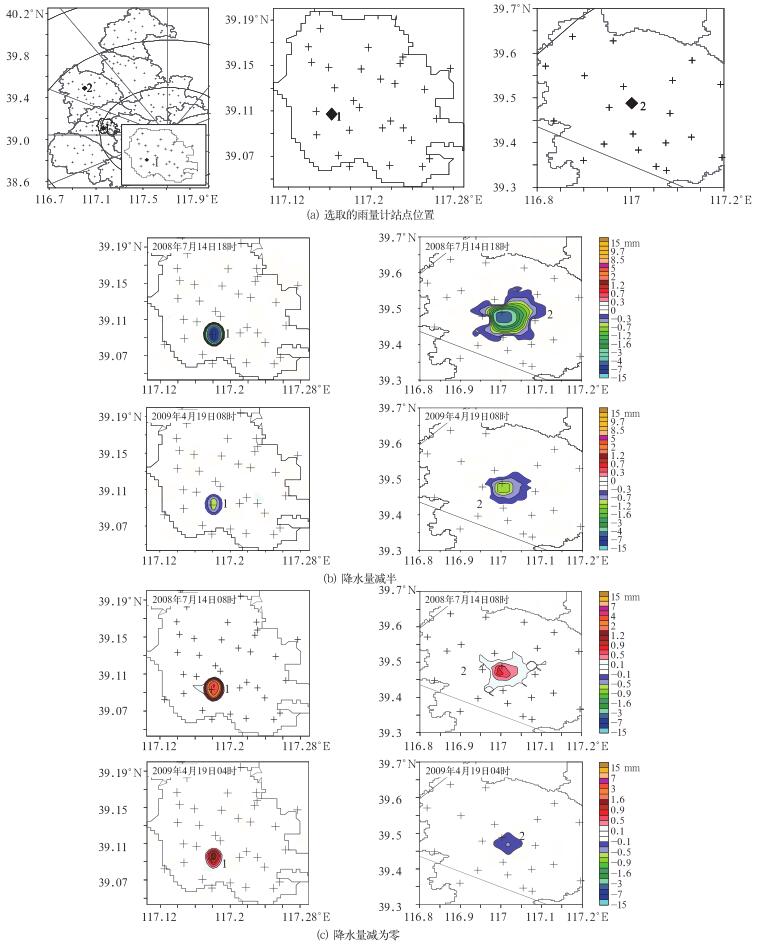
在“最大密度雨量计网”中任意选取不同站点,任意增大或减小其的降水量值,然后重新对雷达进行校准,对比分析其估测结果(下面简称“估测场”)和“真值场”的差异。图 5a所示为两次过程参加校准的“最大密度雨量计网”、1、2为任选的两个站点,从图上看到站点1周围的雨量计分布密度明显大于站点2的。
|
图 5 减小单站降水量对估测降水场的影响(世界时)(a)两次降水过程所选雨量计站点在最大密度雨量计网中的位置,(b)站点降水量减半时的绝对误差分布,(c)站点降水量减为零的绝对误差分布 Fig. 5 Impact of the radar rainfall estimation by reducing single raingauge site precipitation (UTC) (a) the location of the selected raingauge at the maximum density of raingauge net, (b) the absolute error distribution when reduced to the half precipitation of the raingauge site, and (c) the absolute error distribution when reduced to zero of the raingauge site |
将所选站点的降水量值分别减小一半和减小3/4(没有减小到零)时,“估测场”与“真值场”的绝对误差均为负,就是说减小雨量计校准网中任意站点的降水量值均会造成雷达对站点周围降水的低估(图 5b为两次过程雨量计降水量值减半时的绝对误差分布)。对比站点1、2对估测降水场的贡献看到,低估区影响范围与站点周围雨量计分布密度密切相关:站点1周围的雨量计密度大、其低估区的影响范围小;而站点2周围的雨量计密度相对较小、其低估区的影响范围则相应较大。对比不同降水过程的同一个站点看到,当减小的降水量大小相同时,站点周围低估区的范围没有明显的变化,但偏低估计的程度有所不同(图 6),其和站点本身降水量值的大小无关,而和其降水量值减小的多少有关(如站点1),降水量减小的越多,低估的程度越大。对同一站点相同时次减小不同降水量时,雷达对站点周围降水低估的程度及低估区的范围大小均和站点降水量减小的多少有关,降水量减小的多,低估的程度就大、影响范围也大;反之减小的少,低估的程度就小、影响范围也小。当将所选站点的降水量减小到零时,“估测场”与“真值场”的绝对误差有正有负(图 5c和图 6),也就是说将校准雨量计网中任意站点的降水量值变为零,会造成雷达对站点周围降水的偏高或偏低估计。分析看到,高(低)估区的影响范围和站点周围雨量计的密度有关,站点1周围的雨量计密度大、其周围偏高(低)估计的影响范围则小;站点2周围的雨量计密度相对较小、其周围偏高(低)估计的影响范围则相对大些。对“估测场”的贡献是高估或低估?这和所选站点原有的降水量值相对于其周围雨量计降水量平均值的大小有关,当站点周围雨量计的平均值大于站点原有降水量值时,在站点周围出现偏高估计;当站点周围雨量计的平均值小于站点原有降水量值时,在站点周围出现偏低估计。
|
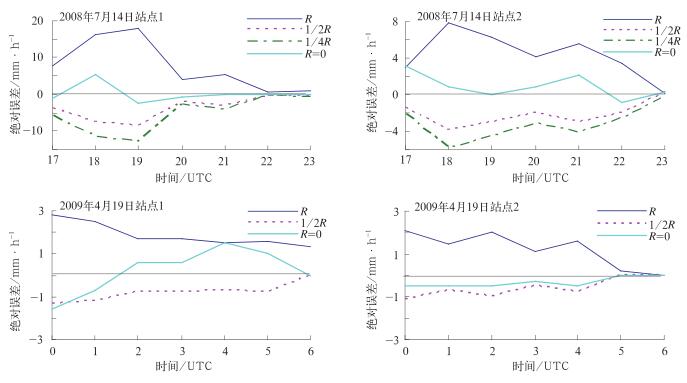
图 6 减小单站降水量对雷达估测降水场的影响 (R表示站点降水量,1/2R表示站点降水量减半,1/4R表示站点降水量减去3/4,R=0表示站点降水量减为零) Fig. 6 Impact of the radar rainfall estimation by reducing single raingauge site precipitation (R is site precipitation, 1/2R the site precipitation reducing the half, 1/4R site precipitation by reducing 3/4, R=0 site precipitation by reducing zero) |
另外从图 6看到,对同一次降水过程的同一站点来说,不同时次站点降水量减小时对雷达估测场的贡献仅与站点降水量减小的多少有关,而和站点本身降水量及不同时次站点降水量的多少无关,其的影响范围也仅和站点周围雨量计的密度有关;再对比两次降水过程同一站点减小相同降水量对估测场的影响看到(图略),雷达对站点周围降水高(低)估的程度及其影响范围也仅和降水量减小的多少有关,而和选取的降水天气过程无关。这说明在校准雨量计网中减小任意单个站点的降水量对雷达估测降水的贡献仅与站点的空间分布及其降水量减小的多少有关,而和降水随时间的演变及天气过程降水类型无关。
3.2.2 增大单个站点的降水量分别将所选站点1、2的降水量值增大10和20 mm,然后重新校准雷达,通过对比分析看到:“估测场”与“真值场”的绝对误差均为正,就是说增大站点降水量使雷达对站点周围的降水估计均偏高;而雷达对降水偏高估计的多少和站点降水量增大的多少相关。计算不同时次两个站点周围偏高估计的最大值和增大的降水量值之间的偏差:偏差=(估测降水量-增大降水量)/增大降水量。看到(表略):虽然两个站点的降水量分别增大10和20 mm,但两次过程的站点1处的偏差均为-3%,而站点2处的偏差小于等于-0.5%,这说明增大站点降水量造成雷达对降水高估的偏差和降水量增大的多少无关,仅和站点周围雨量计的密度有关,周围雨量计分布密度小的站点处的偏差小、分布密度大的站点处的偏差反而大;这进一步说明校准雷达估测降水的雨量计密度不一定很大,而是要有一个最佳密度分布的雨量计网。
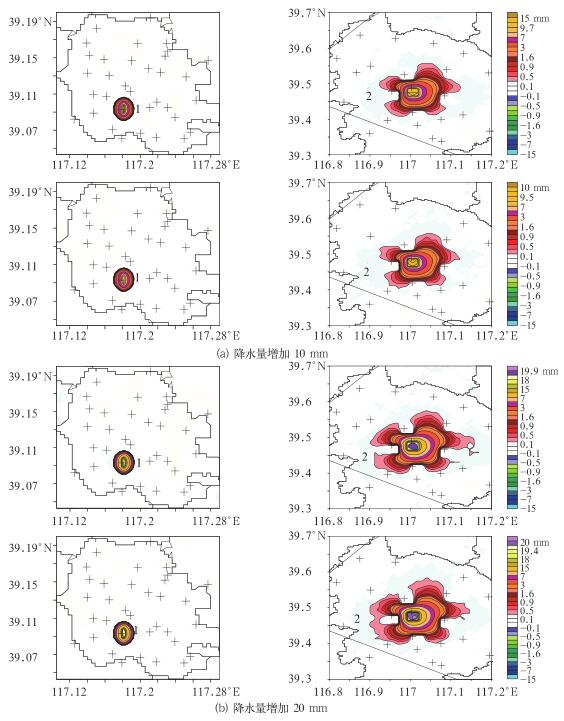
而站点周围偏高估计的范围则和站点降水量增大的多少有关(图 7)。从图 7看到,降水量增大20mm时(图 7b)站点周围高估的范围明显大于增大10 mm时(图 7a)的。另外比较同一降水过程站点1和站点2的周围雷达对降水高估的范围看到,站点1周围高估的范围比站点2的小很多,这说明对同一次降水过程,不同站点增大相同降水量时,其对雷达估测降水高估的范围大小和站点周围雨量计密度密切相关,站点周围雨量计密度越大,其影响范围越小;站点周围雨量计密度越小,其影响范围越大,这和上面分析减小站点降水量对雷达估测降水影响的结论一致。
|
图 7 2008年7月14日19:00 UTC和2009年4月19日03:00 UTC增大单点降水量对估测降水场的影响 (a)站点降水量增大10 mm时的绝对误差分布,(b)站点降水量增大20 mm时的绝对误差分布 Fig. 7 Impact of radar rainfall estimation by increased a single raingauge precipitation at 1900 UTC July 14, 2008 and at 0300 UTC April 19, 2009 (a) the absolute error distribution when precipition increased 10 mm, (b) the absolute error distribution when precipition increased 20 mm |
另外,对比两次过程同一站点增大相同降水量对雷达估测降水的影响(图 7)看到,无论是偏高估计的多少、还是偏高估计区范围的大小都一样,并没有因不同降水过程及不同时刻站点降水量不同而出现差别。这说明增大单站降水量对雷达估测降水的影响仅和站点的空间分布及其降水量增大的多少有关,和降水随时间的演变及天气过程降水类型无关。
4 结论与讨论选取代表不同降水类型的三次降水天气过程,以所有雨量计校准雷达得到的估测降水场作为“真值场”,对比分析了14种不同雨量计密度校准雷达的估测效果,并对“最大密度雨量计网”中任意单个站点对雷达估测降水效果的贡献进行试验分析。有以下几点结论:
(1) 校准雷达的雨量计密度较小时,雷达估测降水的误差较大,估测效果不好;随校准雨量计密度的不断加大,估测误差明显减小、雷达估测降水的精度不断提高并趋于稳定。
(2) 校准不同类型降水需要的雨量计密度不同,对于积云强对流天气,当校准的雨量计密度为196 km2·部-1时,雷达的估测误差可控制在5%以内;当校准积层混合云降水的雨量计密度为226 km2·部-1时,雷达估测降水的误差仅为2%;而对于层云降水天气,校准雷达的估测误差为1.7%时需要的雨量计密度仅为405 km2·部-1。而且校准雷达的雨量计密度不一定很大,使雷达估测降水的精度和“真值场”的相当时的雨量计网最佳密度为121 km2·部-1。
(3) 在雨量计网中任意增加降水量不为零的站点,会在增加的站点周围出现估测偏差,其对估测场的贡献是高估或低估?这和站点降水量相对于其周围雨量计平均值的大小有关,当站点降水量值大于(小于)其周围站点降水量的平均值时出现高(低)估区,这一规律出现的概率为72%。而高(低)估区的范围则和站点周围雨量计密度相关,当周围雨量计密度大时其影响范围小、周围雨量计密度小时其影响范围大。
(4) 任意增大(减小)校准雨量计网中单个站点的降水量会使雷达对站点周围降水的估计偏高(偏低),高(低)估的程度及影响范围与站点降水量增大(减小)的多少及站点周围雨量计分布密度有关,而和降水类型及降水随时间的演变无关。当站点降水量值增大(减小)的越大,高(低)估的程度越大;同时周围雨量计密度越大的站点周围高(低)估区的影响范围越小,而周围雨量计密度越小的站点周围高(低)估区的影响范围越大。
Imai I.Raindrop size distribution and Z-R relationships[C].Proc Eighth Weather Radar Conf, Boston, AMS, 1960:211-215.
|
James W W, Brandes E A, 1979. Radar measurement of rainfall: A summary[J]. Bulletin of AMS, 60(9): 1048-1058. |
Chapon B, Delrieu G, Gosset M, et al.Study of the Z-R relationship sensitivity on the precipitation type using concomitant ground-based drop size distribution and vertically pointing radar measurements[OL]. 1998:ERAD3-A-00057.
|
Daley R, 1991. Atmospheric Data Analysis[M].
New York: Cambridge University Press, 457.
|
Dinku T, E Anagnostou, M Borga, 2002. Improving radarbased estimation of rainfall over complex terrain[J]. J Appl Meteor, 41: 1163-1178. DOI:10.1175/1520-0450(2002)041<1163:IRBEOR>2.0.CO;2 |
Ahnert P R, Krajewski W F, Johnson E R.Kalman filter estimation of radar-rainfall field bias[C]. In preprints 23rd Conf. On Radar Meteor, 1986, JP33-JP37.
|
Ninomiya K, Akeyama T, 1978. Objective analysis of heavy rainfalls based on radar and gauge measurement[J]. J Meteor Soc Japan, 50: 206-210. |
Krajewski W F, 1987. Cokriging radar-rainfall and rain gauge data[J]. J Geophys Res, 92(d8): 9571-9580. DOI:10.1029/JD092iD08p09571 |
Rosenfeld D, Wolff D B, Amitai E, 1994. The windows probability matching method for rainfall measurements with radar[J]. J Appl Meteor, 33: 682-693. DOI:10.1175/1520-0450(1994)033<0682:TWPMMF>2.0.CO;2 |
Wilson J W, 1970. Integration of radar and raingage data for improved rainfall mesaurement[J]. J Appl Meteor, 9: 489-498. DOI:10.1175/1520-0450(1970)009<0489:IORARD>2.0.CO;2 |
Brandes E, 1975. Optimizing rainfall estimates with the aid of radar[J]. J Appl Meteor, 14: 1339-1345. DOI:10.1175/1520-0450(1975)014<1339:OREWTA>2.0.CO;2 |
Koistinen J, Puhakka T.An improved spatial gauge-radar adjustment technique[C]. Proc 20th Conf on radar meteorol, AMS, 1981:179-186.
|
Herndon A, Woodley W L, Miller A H, et al.Comparison of gauge and radar methods of convective precipitation measurement[C]. NOAA Tech Mem, 1973:ERLOD-18.
|
Harrold T W, English E J, Nicholass C A, 1974. The accuracy of radar-derived rainfall measurements in hilly terrain[J]. Quart J R Met Soc, 100: 331-350. DOI:10.1002/(ISSN)1477-870X |
Woodley W L, Olsen A R, Herndon A, et al, 1975. Comparison of gages and radar methods of convective rain measurement[J]. J Appl Meteor, 14: 909-928. DOI:10.1175/1520-0450(1975)014<0909:COGARM>2.0.CO;2 |
刘黎平, 牟容, 许小永, 等, 2007. 一次飑线过程的动力和微物理结构及滴谱变化对降水估测的影响研究[J]. 气象学报, 65(4): 601-611. DOI:10.11676/qxxb2007.055 |
张培昌, 戴铁丕, 傅德胜, 等, 1992. 用变分方法校准数字化天气雷达测定区域降水量基本原理和精度[J]. 大气科学, 16(2): 249-256. |
刘晓阳, 杨洪平, 李建通, 等, 2010. 新一代天气雷达定量降水估测继承系统[J]. 气象, 36(4): 90-95. DOI:10.7519/j.issn.1000-0526.2010.04.016 |
李建通, 张培昌, 1996. 最优插值法用于天气雷达测点区域降水量[J]. 台湾海峡, 15(3): 255-259. |
李建通, 高守亭, 郭林, 等, 2009. 基于分步校准的区域降水量估测方法研究[J]. 大气科学, 33(3): 501-512. |
黄小玉, 陈媛, 熊毅, 等, 2009. 漂移克里金方法在雷达和雨量计联合估测降水中的应用[J]. 气象学报, 67(2): 288-297. DOI:10.11676/qxxb2009.029 |
张培昌, 杜秉玉, 戴铁丕, 2001. 雷达气象学[M]. 北京: 气象出版社.
|
王建林, 刘黎平, 曹俊武, 2005. 双线偏振多普勒雷达估算降水方法的比较研究[J]. 气象, 31(8): 25-30. DOI:10.7519/j.issn.1000-0526.2005.08.006 |
王叶红, 崔春光, 赵玉春, 等, 2001. 变分技术在校准数字化天气雷达定量估测降水的应用[J]. 气象, 27(10): 3-7. DOI:10.3969/j.issn.1000-0526.2001.10.001 |
王建林, 徐晓亮, 毕玮, 等, 2008. 变分校准法在山东雷达估测降水中的一次应用[J]. 气象, 34(S1): 219-222. DOI:10.7519/j.issn.1000-0526.2008.S1.040 |
丛芳, 刘黎平, 2011. 新一代天气雷达与地面雨量资料的综合分析[J]. 气象, 37(5): 532-539. DOI:10.7519/j.issn.1000-0526.2011.05.003 |
陈晓辉, 曹俊武, 胡志群, 等, 2010. 车载X波段双线偏振多普勒天气雷达及其数据处理系统[J]. 气象, 36(8): 116-125. DOI:10.7519/j.issn.1000-0526.2010.08.017 |
刘黎平, 王致君, 1996. 双线偏振雷达探测的云和地物回波的特征及其识别方法[J]. 高原气象, 15(3): 303-310. |
刘黎平, 吴林林, 杨引明, 2007. 基于模糊逻辑的分布式超折射地物回波识别方法的建立和效果分析[J]. 气象学报, 65(2): 253-260. |
 2012, Vol. 38
2012, Vol. 38 