引言

随着电力事业的发展，气象灾害对输电线路安全的影响与日俱增。特别是电线积冰成为冬季影响输电线路的主要灾害。除南岭以南等少部分地区, 我国大部分地区几乎年年都有不同程度的导线积冰或积冰事故。陕西南北狭长、地形复杂，气候多样。从历史资料看，秦岭、巴山、宜君梁等地的导线积冰严重，因此，如何比较合理地确定设计冰厚就成了设计输电线路工程工作面临的重要问题。

从国外来看，美国、加拿大早已有关于电线积冰的相关研究^[1]，20世纪80年代，挪威电力部门和气象部门合作，利用近30年积冰实测资料和常规气象资料，进行积冰的系统研究^[2]。前苏联在高耸建筑物如广播铁塔、电视塔、跨江送电线路铁塔的积冰研究方面取得过很大进展^[3-4]。朱瑞兆、谭冠日等^[3-4]作了很多研究。各地科研人员对电线积冰现象进行了大量研究，对积冰的观测^[5-6]，雪、雨凇、雾凇的气候特征^[7-8]，形成积冰的气象条件，物理过程^[9-11]以及积冰的时间地理分布、气候特征、资料应用和冰灾防御等^[12-16]作了分析。

电线是否积冰与气象条件密切相关。积冰要具备低温、高湿天气，大量的雨凇、雾凇、降雪天气发生时，就可能会出现较厚的电线积冰。本文对陕西全省各地的常规气候资料和少部分的积冰观测资料进行分析计算，参考电力部门输电线路所做的部分电线积冰观测资料与多年积累的积冰灾情资料，找出它们之间的内在联系，建立数学模型。将多年一遇的积冰厚度计算到空间每一个点上，作出陕西全省电线积冰厚度的分布，绘制了30年一遇、50年一遇全省1：500000积冰分布图。可作为陕西省电网建设中积冰厚度设计的重要依据。

1 华山气象站实测积冰资料计算

陕西省共有11个电线积冰观测站，宝鸡、彬县、定边、华山、洛川、绥德、铜川、吴起、西安、榆林和凤翔。其中大部分站观测资料不连续、年代短，无法使用，只能作为参考。只有华山站有连续系统的观测资料，同时华山气象站地处秦岭山区，而陕西省的重冰区主要分布在秦岭，所以华山的资料有较强的代表性。本文首先以1980—2007年华山电线积冰观测资料为主进行计算分析。

1.1 积冰厚度计算

平常所观测到的积冰的直径、厚度^[17]，并不能真正说明积冰的程度。因为每次积冰的密度是不一样的。有时外形大但密度小、重量轻，有时外形小但密度大、重量重，为了比较，必须换算成统一比重的标准积冰厚度(我国规定为0.9 g·cm^-3)。根据华山历年实测的积冰资料，每年挑选出一个重量最重的数值。只要根据每次观测到的积冰重量, 通过以下公式计算就可换算成统一比重均匀裹覆电线的积冰厚度。从而得到华山历年标准积冰厚度。

单位长度上积冰的体积

$V=\pi \left( \frac{D}{2} \right){{~}^{2}}\times 1-\pi \left( \frac{\phi }{2} \right){{~}^{2}}\times 1=\frac{\pi }{4}({{D}^{2}}-{{\phi }^{2}})$

式中，V为积冰1 m长的圆筒体积，D为积冰1 m长的圆柱体的直径(包括模拟线)，φ为积冰观测模拟线的直径。

单位长度上积冰的体积的重量

$W=V\rho =\frac{\pi }{4}({{D}^{2}}-{{\phi }^{2}})\rho $

式中，W为积冰1 m长的圆筒体积的重量，ρ为积冰密度。

因为

$D=2b+\phi $

式中，b为2 m高处^[17]积冰圆筒体积的厚度，也称冰厚。

所以

$\begin{align} & W=V\rho =\frac{\pi }{4}(4{{b}^{2}}+{{\phi }^{2}}+4b\phi -{{\phi }^{2}})\rho \\ & \quad =\pi \rho {{b}^{2}}+\pi \rho \phi b \\ & \quad {{b}^{2}}+\phi b-\frac{W}{\pi \rho }=0 \\ \end{align}$

(1)

积冰厚度

$b=\{-\phi +{{[{{\phi }^{2}}+4W/\left( \pi \rho \right)]}^{1/2}}\}/2$

(2)

式中，π=3.1416, ρ=0.9, φ=4。所以

$b=-2+\left( 0.3537W+4 \right){{~}^{1/2}}$

因此由式(2) 便可计算出华山历年标准积冰厚度。

1.2 距地10 m高冰厚订正

设计风速的计算高度^[18]和重现期，330 kV及以下架空送电线路要求离地15 m高、15年一遇; 500 kV架空送电线路要求离地20 m高、30年一遇。

同理，架空送电线路设计高度^[18]冰厚应采取以下标准:330 kV及以下等级为离地15 m高，15年一遇，冰的厚度密度为0.9 g·cm^-3的标准冰厚; 500 kV为离地20 m高、30年一遇。而根据最新规范规定^[19]设计高度全部为10 m，是为了便于比较。

${{K}_{h}}={{(\frac{h}{{{h}_{0}}})}^{\alpha }}$

式中，K_h为距地面高度订正系数，h为设计导线距地面高度^[19], h₀为观测模拟线距地面高度为2 m，α指数，根据规范规定取^[19]0.22, 所以K_h为1.4249。

距地面10 m高度处的积冰厚度

${{b}_{10}}={{K}_{h}}b$

(3)

从而计算出华山历年10 m高度处标准积冰厚度。

1.3 积冰厚度与常规气象要素相关分析

电线积冰必须具备气温0℃以下，相对湿度90%以上的条件。所以应对气温、相对湿度相联系的气象因子做详尽的分析。通过对华山气象站的积冰观测资料分别与历年各月、年的平均气温、最低气温、相对湿度、降水量、降水日数、年雾凇最长持续小时数、年雨凇最长持续小时数、年雾凇日数、年雨凇日数和年降雪日数等众多气象要素做相关分析，最终找到了与积冰相关较好的因子：年雾凇日数、年雨凇日数、年降雪日数、年雾凇最长连续小时数和年雨凇最长连续小时数。

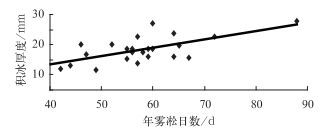
1.3.1 年雾凇日数相关分析

年雾凇日数为当年7月至次年6月出现雾凇天气现象的天数。历年积冰厚度与年雾凇日数相关分析见图 1。

图 1中横坐标为雾凇天数，纵坐标为积冰厚度。其趋势方程为

${{b}_{10}}=0.278{{d}_{ws}}+2.3359$

(4)

式中，b₁₀为积冰厚度，d_ws为雾凇日数。其相关系数为0.6836，通过了置信度为0.01的显著性水平检验。

1.3.2 年雨凇日数相关分析

年雨凇日数为当年7月至次年6月出现雨凇天气现象的天数。历年积冰厚度与年雨凇日数相关分析见图 2。

图 2中横坐标为雨凇天数，纵坐标为积冰厚度。其趋势方程为

${{b}_{10}}=0.4212{{d}_{ys}}+8.6$

(5)

式中，b₁₀为积冰厚度，d_ys为雨凇日数。其相关系数为0.5086，通过了置信度为0.01的显著性水平检验。

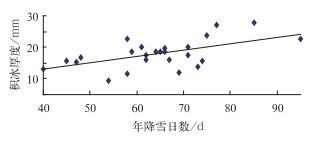
1.3.3 年降雪日数相关分析

年降雪日数为当年7月至次年6月，降雪量≥0.1 mm的天数。历年积冰厚度与年降雪日数相关分析见图 3。

图 3中横坐标为降雪天数，纵坐标为积冰厚度。其趋势方程为

${{b}_{10}}=0.2054{{d}_{jx}}+4.7467$

(6)

式中，b₁₀为积冰厚度，d_jx为降雪日数。其相关系数为0.5707，通过了置信度为0.01的显著性水平检验。

1.3.4 年雾凇最长连续小时数相关分析

年雾凇最长连续的小时数为当年7月至次年6月出现雾凇持续时间最长一次的小时数。

雾凇最长连续的小时数长的年份说明这年某一段时期内，气温低且湿度大的气象条件维持的时间特别长，在低温高湿时间长的情况下往往有利于电线积冰增厚。历年积冰厚度与年雾凇最长连续的小时数相关分析见图 4。

图 4中横坐标为雾凇最长连续的小时数，纵坐标为积冰厚度。其趋势方程为

${{b}_{10}}=0.0345{{d}_{wsl}}+9.2$

(7)

式中，b₁₀为积冰厚度，d_wsl为雾凇日数。其相关系数为0.3854，通过了置信度为0.05的显著性水平检验。

1.3.5 年雨凇最长连续小时数相关分析

年雨凇日数为当年7月至次年6月出现雨凇最长连续的小时数。

雨凇最长连续的小时数长的年份说明这年某一段时期内，这年寒冷时期较长，空气过冷却液态降水多且维持的时间特别长。在这种情况下，往往有利于电线积冰增厚。历年积冰厚度与年雨凇最长连续的小时数相关分析见图 5。

图 5中横坐标为雨凇最长连续的小时数，纵坐标为积冰厚度。其趋势方程为

${{b}_{10}}=0.0348{{d}_{ysl}}+11$

(8)

式中，b₁₀为积冰厚度，d_ysl为雨凇最长连续的小时数。其相关系数为0.3929，通过了置信度为0.05的显著性水平检验。

2 陕西省各地设计冰厚的推算

根据华山气象站的积冰观测资料，挑选历年各月年与积冰相关最好的因子：年雾凇日数和年雨凇日数，反复计算、试验、分析及模拟后得出，年雾凇日数与年雨凇日数相加之和与所对应的年最大积冰厚度有较好的数据依据。根据陕西的地理地形以及多年来积累的电线积冰厚度设计经验，陕西省积冰厚度用式(9) 表示。

${{b}_{10}}=0.1961{{d}_{h}}+2.02$

(9)

式中，b₁₀为积冰厚度(单位：mm)，d_h为年雾凇日数与年雨凇日数之和(日数)。

这里统一使用1961—2007年(跨年度)46年历史气候资料，可得到陕西省各地气象台站所在地46年的积冰厚度。

3 重现期冰厚计算

根据我国新的架空输电线路设计规范^[19-20], 架空输电线路设计冰厚应采取以下标准计算设计冰厚重现期：330 kV及以下等级为30年一遇的冰厚；750和500 kV为50年一遇的冰厚。重现期设计冰厚的计算应采用概率统计法确定线路设计冰厚，其概率模型宜采用极值Ⅰ型分布。本文采用极值Ⅰ型分布作为概率模型, 分别计算30和50年一遇的设计冰厚。

极值Ⅰ型是极值推断中广泛使用的方法^{[3-4, 21-23]}。其分布函数

$F{\rm{ }}({b_P}) = P{\rm{ }}(b{\rm{ ＜ }}{b_P})\exp \{ - \exp [ - a{\rm{ }}({b_P} - u)]\} $

(10)

从分布函数[式(10)]可以看出是双指数形式，所以有时也被称作双指数分布。式中，b为随机变量，即所有的最大积冰厚度，b_P是发生概率为P时的最大积冰厚度，这里为30或50年一遇事件。即P=1/30≈0.033或P=1/50=0.020。b_P为30或50年一遇的最大积冰厚度。a和u为待定参数。根据分布函数，通过用耿贝尔分布的适线法，得到

${b_P}=\bar b{\rm{ }}({\mathit{\Phi }_p}{C_v} + 1)$

(11)

式中，b为历年最大积冰厚度的平均值，Φ_p称为耿贝尔分布离均系数，它只与保证率有关，计算时可查表。C_v是反映相对变动程度的离差系数(或称变差系数)。

${{C}_{v}}=s/\bar{b}=\left( 1/\bar{b} \right){{\{1/\left( n-1 \right)\text{ }[\sum {{({{b}_{i}}-\bar{b})}^{2}}]\}}^{1/2}}$

(12)

式中，s为均方差(或称标准差)，n为资料序列的长度，b_i为序列中第i年的最大积冰厚度。

根据C_v计算出各种概率下的最大积冰厚度计算值，点绘在概率格纸上，依次连接各点，划出一条平滑的曲线。在曲线上读出30和50年一遇积冰厚度值。

3.1 用气象资料计算的30年一遇的最大冰厚

陕西省共有95个气象站的常规观测资料，根据前面的分析，计算出全省95个站点46年历年的积冰厚度。再对每个站点46年历年的积冰厚度利用极值Ⅰ型分布的概率统计方法计算出30年一遇的冰厚，最后就得出全省95个站点的30年一遇的冰厚。但由于秦巴山区是陕西省的重冰区，气象站点稀少。这里选用秦巴山区周围海拔高度较高的(800~2000 m)华山、太白、凤县、洛南、柞水、留坝、佛坪、宁强、宁陕和镇坪等站的30年一遇的冰厚与其对应的海拔高度，建立的回归方程推算出秦巴山区高山区中有代表性的10个点30年一遇的积冰厚度：

${{b}_{10}}=0.0186H-10.5$

(13)

式中，b₁₀为积冰厚度(单位：mm)，H为海拔高度(m)。积冰厚度与海拔高度的相关系数为0.9538, 通过了置信度为0.001的显著性水平检验。

根据现已建成输电线路的经验，有代表性的10个点的海拔高度做了如下处理：高于2800 m的山峰按2800 m计算，即认为2800 m是形成积冰厚度最大的高度。

根据新的架空输电线路设计规范，设计积冰冰区划分为：设计积冰厚度10 mm及以下为轻冰区，大于10小于20 mm为中冰区，20 mm及以上为重冰区。

轻冰区分别按无冰、5和10 mm设计，中冰区分别按15和20 mm设计，重冰区分别按20、30、40和50 mm等设计。

这就得出了陕西省30年一遇最大积冰冰厚分布图(图 6)。

同理也可计算得出陕西省50年一遇最大积冰冰厚分布图(略)。

3.2 积冰设计厚度

本次冰区划分主要以气象站多年实测积冰资料及常规气象要素为基础，用概率统计的方法计算不同重现期冰厚及其分布规律，辅之全省已有线路观冰数据(330工程的关山观测站、陕西省的820观测站和秦岭宝鸡观冰站)、已建线路设计运行资料(包括电力、邮电、长话等线路以及交通部门、电视转播台和微波站等)、事故及冰灾调查结果和多年工程经验。

积冰设计厚度取值比照参考值，是在积冰观冰、线路设计、运行和事故调查的基础上，根据多年工程经验对计算的数值进行订正后所推荐的数据。

从陕西省最大积冰分布的区域分析, 大部分分布在宝鸡西南地区、关山地区，北部塬区及宜君、铜川、永寿梁和秦巴山区。

3.2.1 冰区分级

输电线路设计中习惯把冰区称为轻冰区、中冰区和重冰区，本次冰区分级是为了绘制分区图。根据使用的需求，冰区划分方法及分级见表 1。

将陕西省分为6个积冰区，分别绘制全省不同区域30和50年一遇的1：500000积冰分布图，每个地区一幅，30(见图 7)和50年一遇各10幅。

3.2.2 各冰区划分的说明

(1) 一级区

主要包括以下地区：关中平原地区，海拔在500 m以下区域；汉中盆地，海拔在600 m以下区域；安康盆地，海拔在600 m以下区域。

(2) 二级区

这一区域主要分布在陕西省除5 mm区及高海拔山区、塬区以外的大部分地区。

(3) 三级区

这一区域分布不太规律，多位于平地连接山区(或塬区)、地形突变地段、低海拔与高海拔过渡区域，以及重冰区与5~10 mm的过渡地带。

(4) 四级区

这一区域分布不太规律，多位于平地连接山区(或塬区)、地形突变地段、低海拔与高海拔过渡区域，以及重冰区与10~15 mm冰区的过渡地带。

(5) 五级区

主要分布在秦岭山区、米仓山区、大巴山区、六盘山及其余脉的关山、陇山、永寿梁、岐山北山、子午岭及其余脉的宜君梁、黄龙山区等高海拔或微地形区域。

(6) 六级区

分布范围主要位于重冰区高海拔地带，受微地形、微气候双重影响，积冰程度进一步加大。

以上分区，如遇到河流、湖泊、水库等大型水体时，需提高一个等级。

对于微地形及微气候区，由于其影响的范围较小，但影响程度却很严重，加之分布范围很广，应根据具体工程情况实地勘查、分析确定积冰厚度及范围。

4 结语

本文应用华山1980—2007年的电线积冰观测资料，分析了电线积冰与气象要素之间的关系，进而推算出陕西省95个站点的电线积冰情况，根据架空输电线路设计规范的相关规定，计算设计冰厚，对陕西省电线积冰进行了区划。同时紧密结合电力建设需求，通过综合分析得出下列结论。

(1) 最大积冰厚度与年雾凇日数、年雨凇日数相关较好，同时都为正相关。即年雾凇日数、年雨凇日数越多积冰厚度越厚，物理意义明确。

(2) 最大积冰厚度在陕西全省的分布，平原盆地小于丘陵浅山区，丘陵浅山区小于高山区。

(3) 最大积冰厚度与海拔高度有较好的相关关系，利用秦岭周围浅山区、米仓山和大巴山周围浅山区部分台站的积冰厚度推算出秦岭、米仓山区和大巴山区无台站高山区的积冰厚度。

(4) 将全省分为6个冰区。其中积冰较重的五级和六级冰区主要分布在秦岭山区、米仓山区、大巴山区、六盘山及其余脉的关山、陇山、永寿梁、岐山北山、子午岭及其余脉的宜君梁、黄龙山区等高海拔或微地形区域，这也是防冰抗冰的重点区域。

(5) 目前从经济角度考虑，无论电力部门还是气象部门不可能布设很多电线积冰观测站进行长时间的观测，所以充分利用完整、系统、长系列的常规气象资料推算多年一遇最大积冰厚度的分区，是可行的、经济实用的方法。