引言

能见度、气温等气象要素直接影响到冬奥会各项目的顺利开展，同时也可能影响到运动员水平的发挥。为给2010年第二十一届冬奥会赛场组委会、参赛人员和观众提供更准确的天气预报服务，由加拿大环境部、德国波恩大学、美国国家大气研究中心(NCAR)、俄克拉何马国家风暴实验室、中国气象局等各国科学家组成的团队，参加了世界气象组织(WMO)批准的世界天气研究计划(WWRP) SNOW-V10(Science and Nowcasting Olympic Weather for Vancouver 2010)。在此次天气服务中，中国气象局以自主开发的GRAPES (Globe/Regional Assimilation and Prediction System)模式，有针对性地对奥运场地多气象要素(相对湿度、气温、露点气温、风向和风速等)进行了精细化预报。

GRAPES模式是在中国气象局与国家科技部共同支持下, 我国自主研发的新一代数值预报模式。它兼顾全球与有限区两种性质不同的预报区域，填补了我国数值预报领域的数项技术空白^[1-6]。2004年GRAPES开始在国家气象中心数值预报室做业务试运行，2005年6月下旬正式在中央气象台投入业务试运行，2006年7月GRAPES模式通过业务化验收并投入业务运行^[7]。从模式对台风、暴雨和冬季大雪等实时应用试验结果看，GRAPES模式对中尺度系统预报模拟的能力和潜力得到了初步的显示^[8]。

数值预报理论的不断发展完善，加上高速度、大容量的巨型计算机及网络的快速发展，使其成为天气预报的基础和重要工具^{[2, 4, 9-10]}。然而，大气是一个极其复杂的系统，天气要素如降水是一个非线性、不确定性和时变的过程，受多种因素影响^[11]，天气预报也因其直面固有的可预报性挑战而成为永恒的科学难题^[12]。针对这一难题，学者们在数值模拟及敏感性试验方面开展大量工作^[13-15]。但如何正确理解数值预报产品并对模式存在的问题和不足进行检验总结，对提高数值预报效果起着至关重要的作用，在很多国家各类预报产品的检验已经成为提高天气预报准确率的有效途径^[9]。张建海等^[16]指出定性定量评估数值产品和预报性能、预报技巧及误差分布特点，对研发人员和预报员都是十分有益的。有关GRAPES模式预报的检验工作已经很多^[17-22]，其中大多数是针对降水的评估。如庄照荣等^[17]用不同分辨率的模式预报差异估计了GRAPES模式的预报误差，并指出模式误差随分辨率降低而线性增加，随预报时效增加呈线性增长趋势；李勇等^[20]通过GRAPES模式对淮河流域降水位置和降水量的预报检验，表明采用分辨率为15 km的预报结果比30 km的预报更接近实况；康岚等^[21]评估了GRAPES模式对西南夏季2 m气温的预报情况；王雨^[23]也对夏季青藏高原中南部降水预报进行了检验。然而，以往的研究主要是针对较长(12或24 h)时效预报产品进行的，对GRAPES模式冬季复杂地形下多气象要素短时预报产品的检验仍较少^[24-25]。

本次冬奥会赛场地形复杂，且需要做时间和空间尺度更小的精细化预报，这种复杂地形下的冬季短时精细化预报无疑将给GRAPES-Meso模式带来极大挑战。为认识GRAPES-Meso对冬季复杂地形区天气预报的问题，改进模式预报效果，完善模式，提高短时天气预报准确率。本文将通过2010年第二十一届温哥华冬奥会和残奥会期间(2010年2月1日至3月31日)，GRAPES-Meso对各个场馆逐时预报和观测资料，评估其在冬季高海拔复杂地形下各气象要素的预报性能。

1 GRAPES-Meso在SNOW-V10中的应用 1.1 SNOW-V10简介

为研究冬季复杂地形上的短时天气预报问题，同时给2010温哥华冬奥会提供可靠的天气预报服务，世界气象组织(WMO)世界天气研究项目组(WWRP)授权一批科学家，来负责将数值预报模式应用在冬季复杂地形上的短时天气预报研究项目^[26](SNOW-V10)。来自加拿大、美国、中国、瑞士、芬兰、德国、奥地利和澳大利亚等相关部门参加了SNOW-V10项目的研究。此项目的主要目的是认识和改进复杂地形区冬季短期预报，特别是像对能见度、风向、风速、相对湿度、降水、云量、气温等重要天气要素的预报效果，以便发展和改进中尺度及陆面模式预报系统，提高短临预报能力，最终评估对终端用户的参考价值。项目借鉴2008年北京奥运会和2000年悉尼奥运会的成功经验，对奥运会赛区布设大量观测网，并使用高分辨率模式，为2010年冬奥会各赛事提供了大量有指导意义的天气预报产品。

目前世界气象组织WWRP开展的短临预报项目^[27]主要有悉尼2000 FDP (重点是夏季对流短时预报)、北京2008 FDP (重点是夏季对流短时预报)和温哥华2010 (SNOW-V10 FDP/RDP)(重点是冬季复杂地形的短时预报)。SNOW-V10是首次冬季天气预报项目，可供参考的经验很少，且温哥华冬奥会赛场地形复杂，加上冬季多雨雪，能见度低，都使SNOW-V10面临巨大挑战。同时大多数预报员并不擅长高山地区气象预报，对气温、相对湿度和风等的预报将主要依靠中尺度模式预报结果，且SNOW-V10项目的许多参与组对该冬奥会地区复杂山区地形效应并不熟悉，模式运行和预报都将面临许多困难，对复杂地形上冬季天气预报需要各个参与者的共同努力。

1.2 SNOW-V10期间GRAPES-Meso的实时运行

数值天气预报经过近一个世纪的发展，已成为每天气象预报不可缺少的重要基础和手段。本次实时预报服务过程中，模式区域设置采用两层嵌套网格(图 1)，表 1中列举了GRAPES-Meso模式的分辨率，格点数，内、外层网格中心点以及物理过程参数化方案设置等基本信息。模式每天00时和12时(世界时，下同)对奥运会各赛区天气要素[地表温度(2 m)、露点温度、相对湿度、风速、风向和降水量等]分别预报两次，其中还包括累积降水量(过去24小时或过去3小时)、各层的位势高度和水平风(200、300、500、700、850和925 hPa)、相对湿度(700、850和925 hPa)、海平面气压、气温等图形产品。

2 检验资料和方法 2.1 资料

站点信息如表 2所示，可以看出6个站点的经纬度比较接近，但海拔高度分布范围广，从海拔最低的WSK (52.1 m)到最高的VOA (1640.0 m)。为了由低到高覆盖尽可能大的海拔高度范围，因此选取了卡拉汉山谷(VOD)、布莱克科姆基地滑动中心(VOI)、惠斯勒山中站(VOL)等6个赛场作为检验站点。限于观测和预报资料，本文将GRAPES-Meso (15 km)数值模式在温哥华冬奥会和残奥会期间(2010年2月1日00时至3月31日23时(UTC，下同)对表 2中6个场馆的逐时气温(定时)、相对湿度(定时)、风速(定时)和风向(八方位风分类检验)预报结果，以站点对站点的方式进行检验评估。

2.2 检验方法

本文主要采用预报准确率、平均误差ME、平均绝对误差MAE及Alpha Index^[28]4种指标来检验GRAPES-Meso模式对气温、相对湿度、风速和风向的预报性能(以下F_i为预报值，O_i为观测值)。

(1) 预报准确率指预报正确的站(次)数与预报总站(次)数之比。参照中国气象局《天气分析预报质量检验方法》^[29]中的规定：

$气温：|F_i-O_i|≤1℃或|F_i-O_i|≤2℃$

(1)

$相对湿度：|F_i-O_i|≤10%$

(2)

$风向：|F_i-O_i|≤22.5 (八方位分类检验)$

(3)

$风速：|F_i-O_i|≤2 \rm{m·s}^{-1}$

(4)

若要素满足以上相应的检验公式，可以认为预报是正确的，例如气温预报准确率指气温预报值与观测值之差的绝对值小于1℃或2℃的百分率，依此，类似定义相对湿度、风向和风速的预报准确率。

(2) 平均误差ME

$ME=\frac{1}{N}\sum\limits_{i=1}^{N}{{}}({{F}_{i}}-{{O}_{i}})=\overline{F}-\overline{O}$

(5)

理想分为0，计算时正负误差抵消，代表模式的系统误差，正误差表示高于预报而负误差表示低于预报，对于订正模式产品预报最有用。如果与平均绝对误差联用，可以判断进行偏差订正的可信度。当平均误差与平均绝对误差接近时，说明系统误差明显，可以当作系统误差进行模式订正。

(3) 平均绝对误差MAE

$\text{MAE}=\frac{1}{N}\sum\limits_{i=1}^{N}{{}}{{| {{F}_{i}}-O }_{i}|}$

(6)

(4) Alpha Index

$AI=\frac{\sum\limits_{i=1}^{N}{{}}{{({{F}_{i}}-{{O}_{i}}-\overline{F}+\overline{O})}^{2}}}{\sum\limits_{i=1}^{N}{{}}{{({{F}_{i}}-\overline{F})}^{2}}+\sum\limits_{i=1}^{N}{{}}{{({{O}_{i}}-\overline{O})}^{2}}}$

(7)

AI(Alpha Index)的取值范围为0到2，理想分为0，它是无偏的误差方差标准化度量。由于误差幅度的平均状况(RMSE)，不能表征误差的偏离方向，同时也不能区分模式的系统误差和随机误差，当变量数值越大，RMSE也就更大，这样容易造成认为模式的预报性能差的误解。Alpha Index可以克服RMSE存在的问题，为将来的模式发展和数值预报检验技巧提供更明朗的方向。Alpha Index量化了关于随机误差的技巧，指数接近0，表示随机误差小，且预报值和观测之间吻合好；指数接近1，表示随机误差大，且预报和观测之间吻合较差；指数接近2，说明随机误差小，预报和观测吻合差，两者趋于负相关^[28]。对于具有相对可靠的物理过程的模式，Alpha Index应该基本小于1。

2.3 降水检验方法

文章对GRAPES-Meso模式预报的24小时累积降水量划分为≥0.1 mm (晴雨)、0.1~10.0 mm (小雨)和≥10.0 mm (明显降水)3个级别，分别计算分析各降水等级的TS评分(TS)、预报正确率(EH)、漏报率(PO)、空报率(NH)、偏差(B)、ETS评分(ETS)，表 3为各指标的简要描述^[30-33]。其中，NA为有降水(即实况和预报均为有)预报正确站(次)数, NB为空报(即实况无而预报有)站(次)数, NC为漏报(实况有而预报无)站(次)数, ND为无降水(实况和预报均为无)预报正确的站(次)数。

3 检验结果及分析

表 4是6个站点气温、相对湿度和风在整个检验期间预报准确率和AI指数。从预报准确率来看，模式对海拔最低的WSK和海拔最高的VOA的气温预报较差。气温误差小于2℃的准确率远高于小于1℃的预报准确率，VOA上升幅度最大，其气温预报准确率从12.79%上升到31.58%。此外，其他各站对气温的预报准确率基本都在40%左右，最高的预报准确率为44.89%。相对湿度的预报准确率普遍较高，除WSK外，其余准确率都在60%以上，其中VOL相对湿度预报准确率达到了66.76%，这为该地区的高山滑雪赛事提供了可靠的天气服务。虽然对WSK的气温和相对湿度的预报最差，但其风速预报效果最好，预报准确率最高，达到60%以上；尽管对位于最高海拔的VOA风速预报依然不尽人意，但风向的预报检验效果相对不错。气温的AI指数都在0.35以下，相对湿度的AI指数主要在0.4~0.5，可认为，GRAPES-Meso模式对气温和相对湿度的预报与观测吻合较好，随机误差小。而风速和风向的AI指数接近1，说明其预报随机误差大，预报和观测吻合较差。

从四要素总的检验看出，风向的预报准确率最低，都在30%以下；相对湿度的预报性能最好，且最稳定；低海拔WSK和高海拔VOA在四个要素中的预报情况表现不一，各有优劣。总体上看，对VOA的预报效果更差。这可能是由于模式对地形的刻画有较大误差，导致强烈的地形强迫作用，而地面各预报要素，尤其是气温对海拔高度很敏感，所以不同海拔地区，模式对气温的预报性能较差。陈敏等^[34]认为模式地形的强迫作用是地面和对流层预报系统误差的重要来源。康岚等^[21]对GRAPES模式预报西南夏季2 m气温的检验评估，也指出模式中高原地形处理的不真实是气温预报产生误差的重要原因之一。所以有必要对模式进行误差订正^[34-36]。

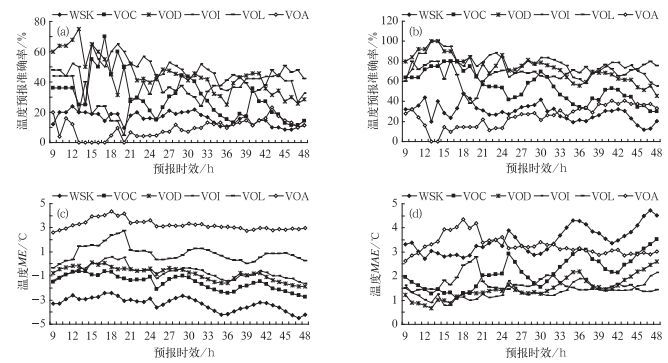
3.1 2 m温度

图 2分别给出了6个场馆逐小时气温预报值与观测值相差小于1℃和2℃预报准确率、平均误差和平均绝对误差情况。从图 2a和图 2b中可以看出，模式对WSK和VOA的预报准确率较低，气温预报误差小于2℃的预报准确率相比于小于1℃的预报准确率，有很大提高。图 2b显示，除WSK和VOA外，其他场馆在时效为12~15 h时，气温的预报准确率是最高的，VOD和VOI在预报时效为13和14 h，小于2℃的预报准确率基本能达到100%。总体上看，随着预报时效的增加，气温预报误差小于1℃或小于2℃的预报准确率缓慢下降或趋于缓慢波动。值得注意的是，开始时VOA的气温预报准确率较低，之后是缓慢上升。这种现象可能是由于VOA的海拔最高(1640.0 m)，模式需要更长的起转(spin-up)时间，然而VOA最终的预报效果还是低于平均水平。从图 2c中看出，除了VOL和VOA的气温预报值偏高外，其他各站预报都低于观测值。随时效的增加，2 m气温偏差呈波浪式变化，且在24、36和48 h附近各站气温偏差达到极大值。图 2d显示，在9~15 h，VOA与其他场馆的变化趋势相反，其余5个场馆MAE先有明显的下降，之后间隔上升与下降变化。总的来看，MAE仍呈增大趋势。

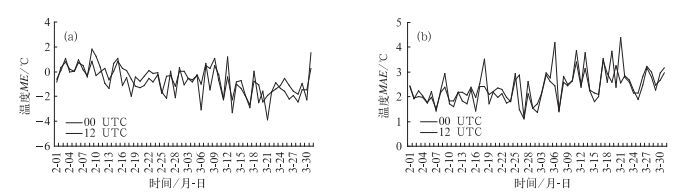
GRAPES-Meso模式气温预报平均误差时序图(图 3a)中可看出，除2月上旬2 m气温预报偏大外，其他检验时段呈负偏差，说明整个冬奥会期间，气温的预报偏低。两不同起报时刻的预报偏差趋势基本一致，12时起报的气温偏差稍大于00时起报的。图 3b显示了整个检验阶段气温预报的平均绝对误差。相比于后期(3月)来说，前期(2月)气温平均绝对误差变化不大，除2月18日，气温的平均绝对误差为3.52较大外，基本在2℃附近波动，但温哥华残奥会期间(3月12—28日)，气温MAE整体增大，其中21日的预报效果最差(MAE为4.39℃)。总的来说，00时起报的气温预报误差基本维持常态，波动要更小于12时起报的。

3.2 相对湿度

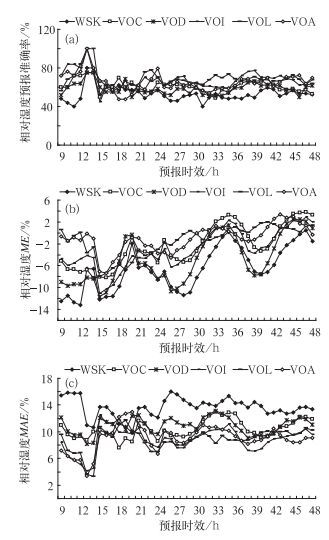
图 4a清楚看出，预报时效小于15 h时，各个场馆逐小时相对湿度的预报准确率逐渐增大，接着迅速降低，之后随预报时效的变化，相对湿度准确率维持在60%左右，基本无明显变化。图 4b显示，GRAPES-Meso对相对湿度的预报明显偏小。预报时效为15、28和40 h时，各场馆分别出现负偏差极大值，说明相对湿度的预报偏干。随预报时效的增加，整体偏差似乎更集中于零。整个预报周期内，相对湿度从预报偏干转变到偏湿。图 4c表明，在检验预报时效内，相对湿度的平均绝对误差在10%徘徊，但WSK的MAE相对稍大，最大MAE为16.01%，各场馆随预报时效的变化趋势基本一致。

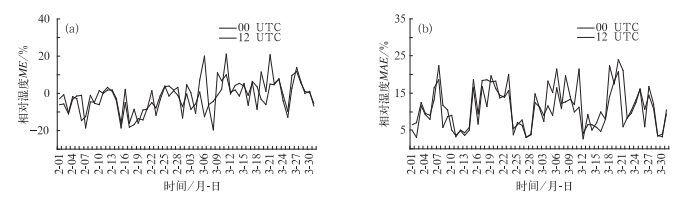
与气温的预报类似，对于不同起报时间的相对湿度平均误差和平均绝对误差(图 5)来说，12时起报的效果要差于00时起报的预报结果，其中3月6、11、21日三天的平均误差达到最大，20%左右(12时起报)。图 5a显示，在整个2月，GRAPES-Meso模式的相对湿度预报偏差小于零，3月的偏差主要为正，这正好与上面3.1中气温的预报偏差随时间变化情况相反。这可能是因为相对湿度与温度呈反比关系，即温度增大，相对湿度减小。所以当气温预报偏高时，相对湿度预报较实况低，反之较实况预报高。相对湿度平均绝对误差(图 5b)表明，温哥华冬奥会期间，相对湿度主要在5%~20%之间变化，波动幅度比气温的更大。

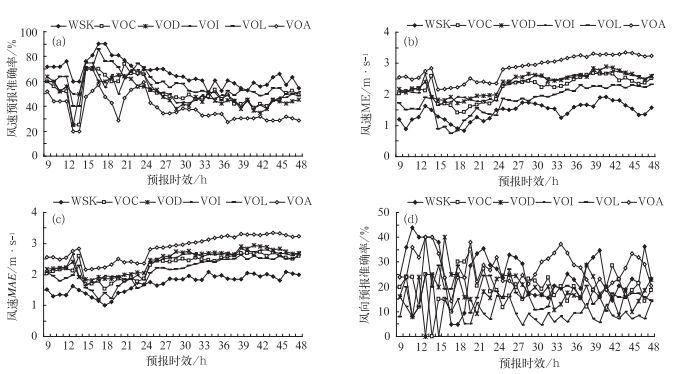
3.3 风向风速

由于风是矢量，这里将主要通过风向和风速的预报准确率来对温哥华冬奥会期间风的预报进行检验。从图 6a可以看到，在预报时效为13和14 h时，各站点风速的预报准确率达到最低，之后准确率迅速上升，预报时效为17 h时，各预报准确率达到最高，尤其是WSK的准确率达到了90%。接着，随着预报时效的增加，预报准确率也逐渐下降。位于最高海拔的VOA仍然是预报效果最差的，对WSK的风速预报效果最好。对比风速和风向的预报准确率(图 6d)，风速的预报准确率高且变化趋势明显，风向的预报准确率普遍比较低，而且变化不均匀。具体来看，风速的预报准确率基本都高于风向的准确率，风速最高准确率可达90.47%，最低也都在20%以上，但风向的预报情况稍差，其准确率主要集中在5%~35%之间，值得一提的是，有些时效的准确率近乎为0，相对于前面检验的气温、相对湿度和风速来说，风向的预报准确率是最低的。对风速的平均误差(图 6b)和平均绝对误差(图 6c)检验表明，随着预报时效的增加，风速的ME和MAE变化趋势很一致，两者都逐渐增大，风速平均误差范围在1~3 m·s^-1。值得注意的是，GRAPES-Meso模式在温哥华冬奥会的风速预报检验中，平均误差始终为正值，表明模式对风速的预报相对于观测值来说偏大。由于风向对局地地形、植被、建筑物等因素很敏感，特别是在风速比较低的情况下，近地面瞬时风向的精确预报并不可靠，只有观测风速达到5 kt (1 kt=0.5144 m·s^-1)以上时才对其风向进行检验^[37]。鉴于低风速时，风向预报多变且极其不稳定，这里仅给出了风向的预报准确率，而没有具体计算其平均误差和平均绝对误差。

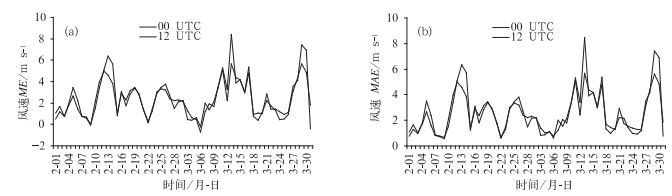
从风速的平均误差和平均绝对误差时序图(图 7)看出，GRAPES-Meso模式在温哥华冬奥会的风速预报检验中，平均误差全为正值，表明模式对风速的预报偏大。两图(图 7a和7b)不仅变化趋势一致，且每天风速的平均误差与平均绝对误差大小接近，说明温哥华冬奥会期间，GRAPES-Meso模式对冬季高海拔复杂地形区的要素预报存在明显的系统误差，可以通过进一步试验和统计分析，对模式地形及系统误差进行订正，进而提高模式预报效果，以便为预报员的预报提供更可靠的指导信息。

3.4 降水

定量降水预报是天气预报和数值预报的难点和重点，为了认识和了解冬季复杂地形下GARPES-Meso模式定量降水的预报水平，我们对2010年冬奥会期间GRAPES-Meso模式的定量降水预报进行初步统计检验。选取检验期间观测和预报都有结果的站点VOI和VOL作为评估对象，将GRAPES-Meso模式24小时累积降水量分≥0.1 mm (晴雨)、0.1~10.0 mm (小雨)和≥10.0 mm (明显降水)3个级别进行检验。

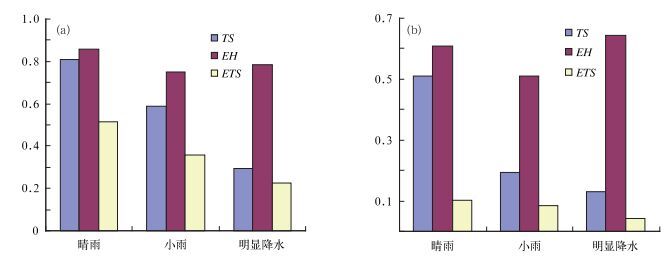
从图 8中可以看出：(1) GRAPES-Meso模式对晴雨的TS评分最高，对小雨和明显降水的评分依次降低。(2) TS评分只反映了预报有雨的正确率，而不能反映更多预报无雨的能力。下面将引进预报准确率EH的评分方法, 它是预报有雨和无雨的正确次数与总预报次数之比, 能全面评估模式预报。对降水预报准确率检验表明，GRAPES-Meso对VOI和VOL小雨的预报准确率最低，分别为75.0%和50.98%。由于预报准确率的评分方法包括气候概率持续预报的正确率, 不能完全反映出预报技巧。(3) 从ETS的评分看出模式对VOI的ETS评分高于VOL，随降水量级的增大，ETS逐渐减小，但ETS评分逐渐靠近TS评分，这与一些研究认为^[38]，随着降水增大，ETS与TS接近的结论是一致的。(4) 总的来说，从VOI和VOL降水的TS、EH和ETS评分来看，VOI都要优于VOL，这可能与其海拔有关，模式对地形高度等的刻画存在一定误差，可能会导致模式对更高海拔的预报效果要相对差一些。

表 5显示的是VOI与VOL两站的漏报空报率统计结果，对小雨而言，漏报率远大于空报率，而随着降水量的增加，情况又有不同，明显降水的漏报率低于空报率。Bias评分表明，GRAPES模式对小雨的预报偏低，而对24小时降水量>10 mm的情况，模式预报的明显偏大，对晴雨的预报偏差最小。

3.5 与其他模式结果的对比

为了更好地认识GRAPES-Meso在温哥华冬奥会期间对高海拔复杂地形下各要素的预报效果，分别将气温、相对湿度和风速的检验结果与其他模式检验结果进行简单对比。限于资料的原因，本文将GRSPES-Meso的检验结果与Huang等^[39]对2010年2月5日至3月21日1 km LAM (Limited-Area version of GEM model)和15 km REG (Regional version of GEM model)的评估结果进行对比。虽然检验时段不是完全一致，但本文只关注对比各个模式对气温、相对湿度和风速预报，在各自检验时段的平均绝对误差。所以可从平均角度了解GRAPES-Meso的预报效果，并通过与其他模式的对比大致了解GRAPS-Meso模式对冬季高海拔复杂地形区各天气要素预报的优劣。

表 6显示了2010年温哥华冬奥会6个场馆气温、相对湿度和风速平均绝对误差的检验结果，其中黑色字体标示的为各个模式对每个要素检验的最大值或最小值。从表 6看出，LAM (1 km)模式的气温预报平均绝对误差明显小于REG (15 km)和GRAPES (15 km)的模式预报。对相对湿度的预报来看，3个模式的预报效果相当，对6个站的相对湿度预报各有优劣。可以看到，在整个检验过程中REG对6个站的风速预报最好，平均绝对误差最小，而相比之下，GRSPES模式对风速的预报比较差，最小平均绝对误差为1.95 m·s^-1，而最大可以达到3.26 m·s^-1。同时可以发现，对于不同的站点，3个模式的性能表现不一。预报员在作决策预报时，可以根据模式的预报评分，对本站预报评分更高的模式加大其参考权重，使模式预报更好地指导决策预报服务。

4 结论

(1) GRAPES-Meso模式预报检验表明，模式对气温和相对湿度的检验效果较好，风速的预报准确率也较高，最高能达到62.39%，对风向的预报准确率基本低于25%，相比于其他各要素，风向的检验效果最差；说明GRAPES-Meso模式对高海拔地形山区气温和相对湿度预报有一定可信度，但对风向的预报结果需加以改进。

(2) 不同起报时间的预报结果存在一定的差异。GRAPES-Meso模式使用00时GFS资料做背景场进行气温和相对湿度的预报效果要优于使用12时GFS资料的预报；而对于风速预报，12时的起报略好。

(3) 从预报时效对6个站的预报进行检验得出：模式对低海拔站点的气温预报偏冷，对高海拔处(VOL和VOA)气温预报偏暖，其误差随预报时效的增加而缓慢增大，预报准确率也小幅度降低；对相对湿度的预报比较稳定，随着预报时效增加，模式对相对湿度的预报有预报偏干转为预报偏湿的趋势；对风速的检验显示，风速预报偏大，随预报时效增加，风速预报准确率显著降低，而风向的预报准确率最低且呈不均匀变化。

(4) GRAPES-Meso模式降水预报检验表明，模式对晴雨预报TS评分最高，随着预报降水量级增大，TS和ETS都逐渐减小，但ETS评分逐渐靠近TS评分。同时Bias评分显示，模式对小雨的预报偏低，而对24小时明显降水预报偏大，对晴雨的预报偏差最小。

(5) 对比GRAPES-Meso、LAM和REG模式的预报检验结果得出，预报员在作决策预报时，可以根据模式的预报评分，对本站预报评分更高的模式加大其参考权重，使模式预报更好地指导决策预报服务。

总的来说，GRAPES-Meso模式作为我国自主研制的数值天气预报模式，在2010年温哥华冬奥会和残奥会期间对各赛场主要天气要素预报表现出一定的预报能力。本工作仅仅是GRAPES-Meso模式对冬季高海拔地区气象要素预报检验评估的初步分析，如果要做更全面的分析，还需更多的资料和检验方法。而且由于检验系统本身存在局限性, 所有的检验结果并不一定能全面而准确地评估每个模式的预报性能, 只能从平均状态了解模式的预报情况。希望此工作对GRAPES-Meso模式的进一步发展完善及应用于冬季高海拔复杂地形下各气象要素的预报工作有一定的参考作用。