2. 湖北省气象服务中心,武汉 430074;
3. 湖北省气象能源技术开发中心,武汉 430074
2. Meteorological Service Centre of Hubei Province, Wuhan 430074;
3. Meteorological Energy Development Centre of Hubei Province, Wuhan 430074
太阳能作为一种可再生和清洁的能源,得到各界越来越多的关注和研究,其应用前景非常广阔。我国太阳能资源丰富,理论储量达每年17000亿t标准煤[1]。近年来,我国光伏发电产业在国家大型工程项目、推广计划和国际合作项目的推动下迅速发展。但是,太阳辐射受天气因素(如云)的影响较大。所以,光伏发电利用自然界能量的同时,也受制于气象条件。为了管理和业务化光伏发电系统,有效利用光波能源就需要可靠的天气预报信息。并且随着太阳能光伏发电量的不断增加,辐射预报也越加显得重要。频繁的预报失误,将会导致巨大的经济损失,进而限制可再生能源的推广。因此,如何预报成为一个新的关键点。
近年来,对太阳辐射的研究观测进展很多[2-3],为光伏电力预报打下一定的基础。周晋等[4]建立了日总太阳辐射月均值的神经网络估算模型,利用实测气象数据资料对神经网络进行训练和检验,检验结果表明此方法是可靠和准确的。徐维[5]进行了短时间尺度太阳辐射数据的时间序列模型(ARMA)的研究,提出了相关的建模、模拟与预报方法,建立了4种时间尺度的ARMA模型,并验证了该模型能够准确反映存在于短时间尺度太阳辐射数据的相关性。2010年,针对光伏发电量的预报研究,湖北省气象局牵头编制了全国“太阳能光伏发电预报系统研究2010年工作方案”、在2010年行业专项“太阳能预报技术研究”中单列一个专题开展太阳辐射预报,这些工作不仅为全国太阳能预报技术研究工作奠定了基础,也将为光伏发电系统的推广和发展提供有力支持和保障。目前,湖北利用取得的发电量资料建立了辐射-发电量预报方程,进行光伏发电量预报试验研究。
现代天气预报方法覆盖着各种不同的应用领域和研究技术。目前,最常用的预报方法可能就是应用数值天气模式提供多种预报时效和多种空间尺度的天气预报。每种方法都有一定的优势,也存在着不足。目前,随着计算机性能的不断改进,大气数值模式分辨率也显著提高,数值天气模式逐渐完善。无论在计算能力还是预报效果方面,中尺度数值天气模式作为业务或者准业务的模式都具有了一定的可行性,得到了广泛的推广和应用。试图解决光伏发电预报能力的重点已经集中在需要大量计算能力和充分考虑了多种物理过程的数值天气预报上。采用数值模式预报模拟技术可以克服观测的局限性,为光伏发电预报提供客观、定量的依据。
美国的多个研究部门及大学的科学家共同参与开发研究了新一代中尺度预报模式和同化系统——WRF模式(Weather Research and Forecast Model)[6-7]。该系统开发的目标是建立一个具有可移植、易维护、可扩充、高效率、用户界面友好的等诸多特性的模式。
本文希望利用中尺度数值模式WRF模拟到达地表短波辐射量,通过批量试验检验中尺度模式对太阳总辐射的预报能力,进而为光伏发电量的预报提供依据。
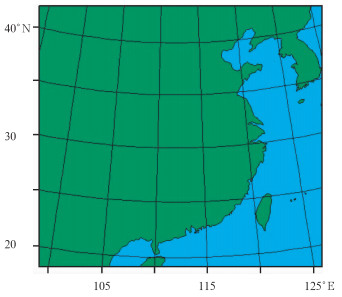
1 试验设计本文使用的WRF模式设置如下:采用一层网格,模式中心位于(31.0°N、112.5°E),水平格点数为201×182(图 1),水平分辨率为15 km,垂直方向有35层,时间步长为60 s。主要的物理过程包括:WRF Single-Moment 6-class微物理方案、Grell-Devenyi ensemble积云参数化方案、RRTM长波辐射方案、Dudhia短波辐射方案、Monin-Obukhov近地面层方案、四层土壤的热扩散方案、MRF边界层方案等。其中Dudhia短波辐射方案来自于MM5模式[8],它简单地计算了由于晴空散射、水汽吸收、以及云的散射、反射和吸收(应用Stephens的云对照表)[9]所引起的向下太阳短波辐射通量[10-11]。
|
图 1 模拟区域示意图 Fig. 1 Diagram of modeling domain |
试验的具体方法:利用NCEP预报场GFS数据作为WRF模式初始场和边界条件,为了与未来实际业务接轨,模式从每日20时(北京时,下同)开始起报,积分36小时,逐小时输出向下到达地表短波辐射通量(Downward short wave flux at ground surface,SWDOWN;单位:W·m-2)。本次批量试验进行了2009年1、4、8和10月共4个月的模拟(缺失GFS数据的部分日期:2009年4月30日12时、8月1-5日12时、8月26日12时)。为了保持时间段的连续性,取12~36 h积分时间段的模拟值进行分析。
2 气象资料与方法选用的观测资料是一级辐射观测站武汉站(30°37′N、114°08′E,海拔高度23.1 m)逐小时到达地面的太阳总辐射——曝辐量(简称太阳总辐射,单位:0.01 MJ·m-2)和每日日间2次(08和14时)云量。模式输出瞬时到达地表短波辐射通量(世界时)乘以0.36近似转换为对应的逐小时的辐射曝辐量(单位:0.01 MJ·m-2),即逐小时太阳总辐射。
3 结果分析在观测实践中发现,云量情况不同,其总辐射也随之发生变化[12]。当观测辐射数据出现异常时,往往需结合当时的天气条件如云量、降水、天气现象等来判断[13],避免错误记录。因此,本文将使用观测的太阳总辐射和云量来对比分析模式的模拟结果。
到达地面的太阳总辐射集中在白天时段,以武汉站为例,将模式模拟的2009年1、4、8和10月的日间逐小时太阳总辐射与实况进行对比分析。表 1为每个月的日间时间段和样本数。1和10月日间时间段共12小时,4和8月日间时间段略长,共14小时。并且根据日间两次观测云量(08和14时),将天气状况分成晴、多云和阴[14], 并统计出不同天气状况对应的逐小时太阳总辐射模拟与实况的样本数(表 2)。
|
|
表 1 1、4、8和10月逐小时太阳总辐射日间时间段和样本数 Table 1 The daylight hours and corresponding number of samples for the Wuhan hourly total solar radiation in January, April, August, and October 2009 |
|
|
表 2 云量分类和对应样本数 Table 2 Cloud cover category and corresponding number of samples |
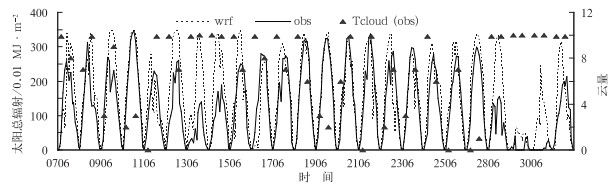
图 2为2009年8月日间模拟与观测的逐小时的太阳总辐射及观测云量时间序列图。从中可以看出,模拟太阳总辐射一般从06时开始出现,并逐渐增加,到中午达到峰值,之后逐渐减小,20时至次日05时为零。该变化趋势与天文辐射基本一致,也与实际观测基本吻合。其中,模式对8月10、16-26和29日模拟太阳总辐射在大小和变化趋势上都与实况非常接近,而在8月13、14、28和30日,模拟效果与观测相差较大。通过分析,当云量覆盖不足3成时,模拟效果通常较好;多云(云量3~7成)的时次数比晴(云量0~3成)的时次数少,这种情况下模拟的太阳总辐射趋势也与实况基本一致;当云量覆盖为9~10成时,尤其是连续几天都是阴天,与前两种情形相比,模拟效果普遍较差;但也有云量为10成时预报较好的例子,如29日观测的逐小时太阳总辐射均在50(单位:0.01 MJ·m-2)以下,模拟结果也在70(单位:0.01 MJ·m-2)以下,与实况基本一致。8月的日间的模拟和观测的相关系数在0.810,通过了置信度0.01的显著性检验(表 3)。
|
图 2 武汉市2009年8月日间模拟与观测的逐小时太阳总辐射以及观测云量的时间序列图 (横坐标:时间,为日和时,下同)单位:0.01 MJ·m-2) Fig. 2 Time series of the Wuhan daylight hourly total solar radiation simulation (dashed) and observation (solid) and observed cloud fraction (right ordinate) for 24 days in August 2009 (x axis:DDHH, unit:0.01 MJ·m-2) |
|
|
表 3 2009年1、4、8和10月日间逐小时太阳总辐射的模拟结果与观测资料的相关系数 Table 3 The correlation coefficients between simulation and observation of Wuhan daylight hourly total solar radiation during 4 months of 2009 |
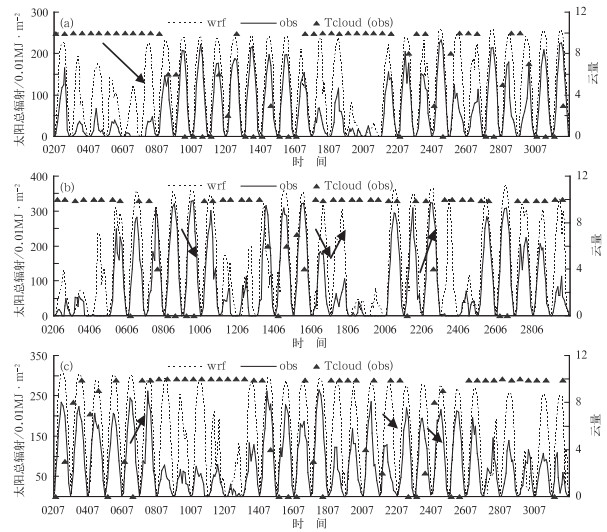
图 3a、3b和3c分别为武汉站2009年1、4和10月日间模拟与观测的逐小时的太阳总辐射时间序列图叠加了两个时次的观测云量。图 4是根据实际观测云量将天气类型分类得出的4个月日间阴、多云和晴的时次数。
|
图 3 武汉市2009年1(a)、4(b)和10月(c)日间模拟与观测的逐小时太阳总辐射以及观测云量的时间序列图 (单位:0.01 MJ·m-2,箭头为变化趋势标记) Fig. 3 Time series of the Wuhan daylight hourly total solar radiation simulation (dashed) and observation (solid) and observed cloud fraction (right ordinate) for January (a), April (b), and October (c) 2009, respectively (unit:0.01 MJ·m-2, arrows show the trend) |
|
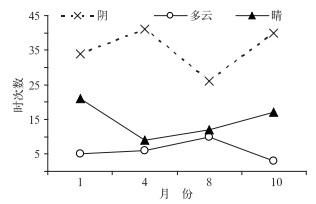
图 4 武汉市2009年1月、4月、8月、10月统计的日间阴、多云、晴的时次数 Fig. 4 Day light times of the clear, broken, or overcast skies in January, April, August and October 2009, respectively |
从图 3中可以看出,模拟的太阳总辐射日变化趋势与天文辐射基本一致,与实际观测结果也基本吻合。1、4和10月日间的模拟和观测的相关系数均在0.8以上,都通过了置信度0.01的显著性检验(表 3)。在图 3a中,1月2-6日太阳总辐射有一次减少的过程,虽然模拟值比观测值偏大,但是仍有下降。1月19和20日模拟值的大小和趋势变化与实际非常接近。4和10月也有类似的情形。
1、4和10月当中,阴天时次较多,其次是晴天,最少的是多云(图 4)。不同天气类型下逐小时太阳总辐射的模拟效果与8月具有相似的特点。可见模式对逐小时太阳总辐射的模拟具有一定的参考价值。
3.3 误差分析本文采用的部分统计量如下:
平均预报误差:
| $ MFE = \frac{1}{N}\sum\limits_{i = 1}^N {\left( {P_f^i - P_o^i} \right)} $ | (1) |
平均绝对误差:
| $ MAE = \frac{1}{N}\sum\limits_{i = 1}^N {\;\left| {\;P_f^i - P_o^i\;} \right|} $ | (2) |
平均绝对百分比误差:
| $ MAPE = \frac{{\frac{1}{N}\sum\limits_{i = 1}^N {\left| {P_f^i - P_o^i} \right|} }}{{\frac{1}{N}\sum\limits_{i = 1}^N {P_o^i} }} \times 100\% $ | (3) |
相对均方根误差:
| $ RRMSE = \frac{{\sqrt {\frac{1}{N}{{\sum\limits_{i = 1}^N {\left| {P_f^i - P_o^i} \right|} }^2}} }}{{\frac{1}{N}\sum\limits_{i = 1}^N {P_o^i} }} \times 100\% $ | (4) |
式中,i表示第i个样本数,N表示样本数,Pfi是第i个模式输出值,Poi是第i个观测值。
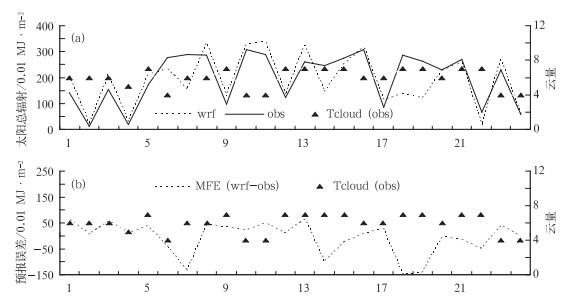
3.3.1 日间各时刻误差统计分析图 5和6是日间各时刻模拟值与实况进行误差统计分析的结果。从图 5看出,平均预报误差(MFE)早晚较小,中午最大, 分布近似拱形。1、4和8月的11-13时的MFE较大,而10月12-14时的MFE较大。8月除了早晚的MFE比其他3个月的略大,其他时刻均小于另外3个月。1和4月MFE比较接近,10月MFE在11-18时明显大于其他3个月。
|
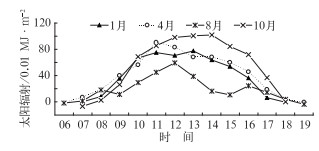
图 5 武汉市2009年1、4、8和10月日间各时刻太阳总辐射模拟和观测结果的平均预报误差(MFE) Fig. 5 The MFE of Wuhan hourly total solar radiation for every daylight hour in January, April, August and October 2009, respectively |
|
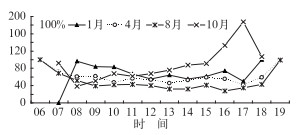
图 6 武汉市2009年1、4、8和10月日间各时刻太阳总辐射模拟和观测结果的相对平均绝对百分比误差(MAPE,单位:%) Fig. 6 The MAPE (unit:%) of Wuhan hourly total solar radiation for every daylight hour in January, April, August and October 2009, respectively |
从平均绝对百分比误差(MAPE)图(图 6)上可以看出,一般情况下,MAPE在早晚较大(除1月07时外),其他时刻比较稳定,变化幅度较小, 模拟的可信度高于其他时刻。1月07时预报与实况非常吻合。8月09-18时之间的MAPE走势较平稳,大小在27%~43%波动,而在早6时和晚19时的MAPE接近100%。4月的MAPE变化趋势类似8月,但数值略大,09-18时的MAPE变化范围在41%~62%。1和10月的MAPE波动较大,两者的变化趋势具有反相位的特点,1月MAPE变化范围不超过100%,但10月MAPE从08时开始一路上升,17时的MAPE近似190%, 18时又下降。
总体来讲,8月日间各时刻的预报效果较好,然后依次为4、1和10月。每个月的09-15时之间的MAPE变化波动较小,模拟的可信度也高于其他时刻,并且该时段到达地表的太阳短波辐射较为充足,具有较高的利用价值。
3.3.2 不同天气类型下的误差统计分析将每天两个时次的逐小时太阳总辐射和云量按照天气类型进行整理分析。图 7~9分别为晴、多云和阴天气类型下模拟与观测逐小时太阳总辐射及观测云量的时间序列图。
|
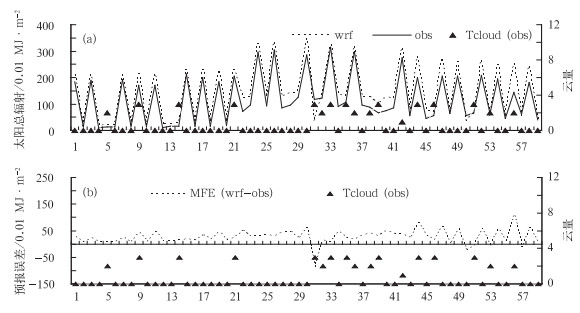
图 7 天气类型为晴时逐小时太阳总辐射模拟和观测结果(a)及对应的预报误差(b) Fig. 7 Time series of the hourly total solar radiation simulation and observation (a) and corresponding forecast errors (b) in clear skies |
晴天共有59个样本。晴天下的模拟与观测变化趋势非常接近(图 7a)。绝大部分是正的预报误差,只有1个时次超过100(单位:0.01 MJ·m-2)(图 7b)。
多云共有24个样本,不足晴天的一半。多云天气的模拟与观测变化趋势基本吻合(图 8a)。预报误差有正有负,负的绝对值最大为149.4(单位:0.01 MJ·m-2)左右,正的预报误差普遍不超过50(图 8b)。
阴天共有141个样本,远多于晴天和多云的时次数。阴天时的云量在7成以上,而云是影响到达地面太阳短波辐射的重要因素之一,因此对阴天的太阳短波辐射模拟具有一定的难度。从图 9a中可以看出,一些时次模拟与实况比较一致,但较前两种天气类型模拟效果,还有一定的差距。预报误差以正值居多,且多在100(单位:0.01 MJ·m-2)以上(图 9b)。
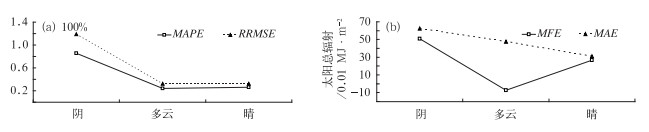
图 10统计出不同天气类型下的MAPE和RRMSE以及MFE和MAE。在阴天的情况下,MAPE、RRMSE和MAE都比较大。在多云和晴天的情况下,两者的MAPE和RRMSE几乎相当,但多云天气下的MAE大于晴天。对于MFE,阴天最大且为正,即预报比实际偏大。多云天气下的MFE为负,不到-20(单位:0.01 MJ·m-2),即预报比实况偏小。晴天天气下的MFE为正。
|
图 10 晴、多云和阴不同天气类型下的MAPE和RRMSE(a)以及MFE和MAE(b) Fig. 10 MAPE, RRMSE (a) and MFE, MAE (b) in clear, broken, or overcast skies |
综上所述,WRFV3模式对太阳总辐射,在不同天气类型下有一定预报能力。阴天天气下模拟的效果普遍不如晴天和多云天气。鉴于多云天气的样本比晴天少,虽然晴天的MAPE略大于多云天气,综合考虑之后,仍以晴天模拟效果最好。
4 结论本文利用中尺度数值模式WRFV3进行了近4个月的向下到达地表短波辐射模拟,并将逐小时输出结果转换成逐小时太阳总辐射进行详细对比和误差分析, 结果表明:
(1) 从总体上看,模拟与实际观测结果的相关性较高,4个月的日间模拟和观测值的相关系数均在0.8以上,且均通过了置信度0.01的显著性检验。模式对太阳总辐射具有一定的预报能力和可信度。09-15时的太阳总辐射较为充足,利用价值较大,这个时段的各时刻模拟的平均绝对百分比误差小于其他时刻。
(2) 模拟结果得到的4个月的时间序列包含了在不同天气条件下地表短波辐射情况。晴天对辐射的预报能力最佳,多云次之,阴天普遍较差。从4个月的时间序列来看,模式对于太阳总辐射的变化趋势具有一定的可信度。
(3) 太阳总辐射预报误差存在的原因,至少部分上,是由于短波辐射方案中使用的云量存在的不确定性或偏差。虽然WRF模式对太阳总辐射预报具有一定的预报能力。但是数值模式并不能十分精确的再现观测。由于太阳辐射资源评估与预报是太阳能光伏发电系统发电量计算(以制定发电规划、电力调度)与预报分析的关键基础之一,所以若直接使用模式输出的辐射值作为光伏发电系统初值仍存在一些误差,可以采用误差订正等方法进行修订,提高数值预报结果的可用性。
简讯, 2005. 我国太阳能储量达每年17000亿吨标准煤[J]. 化工学报, 56(3): 399. |
权继梅, 丁蕾, 郑向东, 等, 2010. 总辐射表两种现场校准方法的比较[J]. 气象, 36(9): 116-119. DOI:10.7519/j.issn.1000-0526.2010.09.019 |
刘香娥, 王广河, 2010. FY-2C静止气象卫星红外通道辐射特性研究[J]. 气象, 36(2): 39-47. DOI:10.7519/j.issn.1000-0526.2010.02.006 |
周晋, 吴业正, 晏刚, 等, 2005. 利用神经网络估算太阳辐射[J]. 太阳能学报, 26(4): 509-512. |
徐维, 2009. 基于时间序列分析的短时间尺度太阳辐射模型研究[J]. 常州工学院学报, 22(1/2): 41-44. |
章国材, 2004. 美国WRF模式的进展和应用前景[J]. 气象, 30(12): 27-31. DOI:10.3969/j.issn.1000-0526.2004.12.006 |
Dudhia J, 1989. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model[J]. J Atmos Sci, 46(20): 3077-3107. DOI:10.1175/1520-0469(1989)046<3077:NSOCOD>2.0.CO;2 |
Lacis A A, Hansen J E, 1974. A parameterization for the absorption of solar radiation in the earth's atmosphere[J]. J Atmos Sci, 31: 118-133. DOI:10.1175/1520-0469(1974)031<0118:APFTAO>2.0.CO;2 |
沈元芳, 胡江林, 2006. GRAPES模式中的坡地辐射方案及其对短期天气过程模拟的影响[J]. 大气科学, 30(6): 1129-1137. |
Skamarock W C, Klemp J B, Dudhia J, et al. A Description of the Advanced Research WRF Version 3[G]. Boulder: National Center for Atmospheric Research, 2008:113.
|
贾东奇, 1996. 浅谈辐射变化规律与辐射观测[J]. 气象, 22(2): 56-57. DOI:10.7519/j.issn.1000-0526.1996.02.016 |
郭发辉, 王颖, 2003. 气象辐射资料准实时处理系统的研制[J]. 气象, 29(7): 19-22. DOI:10.7519/j.issn.1000-0526.2003.07.004 |
Armstrong M A. Comparison of MM5 Forecast Shortwave Radiation with Data Obtained from the Atmospheric Radiation Measurement Program[D].College Park: Univ of Maryland, 2000. http://dpi-journals.com/index.php/IJES/article/view/341
|
 2012, Vol. 38
2012, Vol. 38