2008年汛期开始,中国气象局开始向各级气象部门提供T639模式预报产品。在此之前,管成功等[1]对比了T639和T213模式的预报性能,无论是形势场,还是降水场预报,T639模式都明显优于T213模式。数值模式由于其模式误差和初始场误差的存在,不可避免地会存在预报误差,许多预报工作者对T639模式的预报技巧进行相关的天气学检验,比如:周慧等[2]检验了2008年汛期T639模式降水和各种物理量预报场,发现T639模式预报比T213模式具有较大改进,对亚欧中高纬大气环流背景也有较准确预报。石顺吉等[3]对0903号台风路径预报的检验表明T639的预报结果具有较高的参考价值。其他一些检验也表明T639模式与ECMWF模式预报相比,误差较大,比如对副高西伸脊点预报稳定性较差[4]。T639模式预报是否存在一定的系统误差?如果有,特征如何?消除预报误差中的系统误差后必将有助于预报员更好地使用预报产品。本文利用2009年1月1日至2010年12月31日两年的T639模式预报资料,统计分析了500 hPa高度场、850 hPa的温度场和2 m温度预报场的系统误差,并尝试使用“递减平均法”订正该模式的预报系统误差。
1 资料和方法本文使用的资料为中国气象局一天两次下发至各个省市气象局的T639模式的分析和预报资料,起报时间分别为08和20 BT,预报时效为240小时(10天)。资料空间分辨率为1°×1°,资料范围为整个北半球,时间分辨率为24小时,预报要素包含多个层次的温、压、湿、风等各种气象要素场。此处选取500 hPa高度、850 hPa温度和2 m温度三个要素作为统计分析、检验和订正的对象。
预报系统误差订正试验方法采用“递减平均法”。李莉等[5]利用该方法订正T213降水预报场的系统误差,结果表明该方法对T213的降水预报偏差具有明显改善作用;对T213全球集合预报系统性误差订正研究[6]发现,该方法对形势场和温度场都有不同程度的订正效果。
递减平均法的订正步骤如下:
第一步:误差估计。对于新生成的分析场,计算不同预报时效对于该分析场的预报误差[记为:bi, j(t)],表示如下:
| $ {b_{i, j}}\left( t \right) = {f_{i, j}}\left( t \right) - {a_{i, j}}\left( t \right) $ | (1) |
式中,fi, j(t)为预报场,ai, j(t)为分析场。
第二步:误差累加。将最新的各个时次预报误差累加到上一个时次的误差场,得到更新后的误差场。
| $ {B_{i, j}}\left( t \right) = \left( {1 - w} \right){B_{i, j}}\left( {t - 1} \right) + w{b_{i, j}}\left( t \right) $ | (2) |
式中,w为权重,Bi, j(t-1) 为上一个时次的误差场,Bi, j(t)为累加后的新误差场。
第三步:误差订正。将新的各个时次预报场分别减去累加后的新误差场得到最终的订正场,公式如下:
| $ {F_{i, j}}\left( t \right) = {f_{i, j}}\left( t \right) - {B_{i, j}}\left( t \right) $ | (3) |
式中,Fi, j(t)为订正后的预报场。
根据对比试验,对于500 hPa高度场,w取0.06时订正效果较好;对于850 hPa温度和2 m温度场,w取0.1时订正效果较好(详见2.4节)。检验方法为均方根误差和误差相对订正量,在计算均方根误差时,均采用T639的分析场作为真值,误差相对订正量定义为:订正前与订正后的均方根误差之差与订正前均方根误差的比值。
利用文献[7]中的方法对订正前和订正后的均方根误差的差异进行显著性检验。表 1为500 hPa位势高度、850 hPa温度和地面2 m温度的统计量(t值)的计算结果。查算t分布的查算表可知,对于大于0.05显著性水平检验时t值为1.96。对比表 1可知,对于500 hPa位势高度的订正结果,第1~5天的t值都是大于1.96,第6~10天的t值小于1.96,说明对于前5天的500 hPa位势高度预报场,订正后的均方根误差比订正前具有明显改善;而对于后5天的预报,订正前后的均方根误差序列则未通过显著性检验,订正后的预报场没有明显改善。对于850 hPa温度场和2 m温度场,该订正方法对此两个物理量预报场均有明显订正能力。
|
|
表 1 统计量(t值)的计算结果 Table 1 The result of statistical variable (t value) |
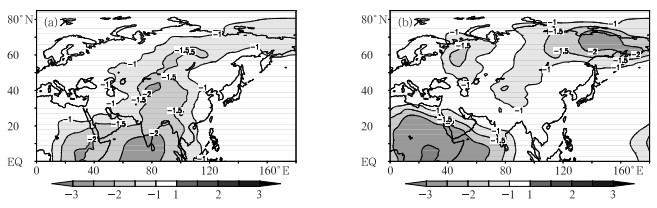
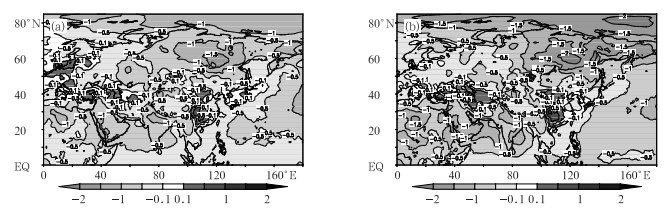
对2009-2010年T639模式对500 hPa位势高度、850 hPa温度和2 m温度的1~10天预报场分别计算平均误差。对于500 hPa位势高度场的预报,平均而言,大部分地区为负的预报误差,预报场的位势高度小于分析场。图 1分别为第3和第6天的平均误差场,第3天(图 1a)的非洲北部至印度洋地区的负值中心较明显,预报场与分析场平均误差可达-20 gpm,到第6天,在亚洲的东北地区和欧洲中部也出现负误差中心,并且随着预报时效的增加,这两个中心越明显。图 2分别为850 hPa温度第3和第6天预报平均误差情况,从图中可以看出,北半球大部分地区也是负温度误差,在亚洲北部负偏差更加明显。另外在我国西南地区至河套地区、西亚地区持续存在温度正偏差,最大可偏高1℃。2 m温度的预报场也具有类似的误差特征(图略)。
|
图 1 2009-2010年500 hPa位势高度预报场与分析场的平均误差(单位:dagpm) (a) 72小时预报, (b) 144小时预报 Fig. 1 The 500 hPa geopotential height average bias between forecast and NCEP analysis for (a) 72 h forecast, and (b) 144 h forecast (unit:dagpm) |
|
图 2 2009-2010年850 hPa温度预报场与分析场的平均误差(单位:℃) (a) 72小时预报, (b) 144小时预报 Fig. 2 The 850 hPa temperature average bias between forecast and NCEP analysis for (a) 72 h forecast, and (b) 144 h forecast (unit:℃) |
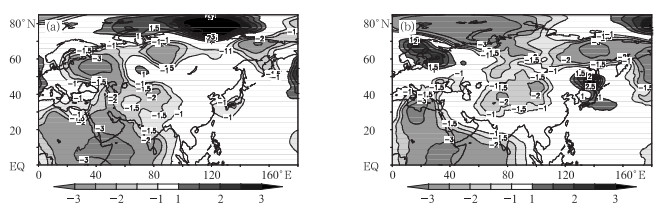
从500 hPa位势高度场不同季节的平均误差分布(图 3)可以看出,对于120小时的预报场,随着季节的变化,平均误差场也发生较大变化,在夏季,高纬地区整体为正偏差,而在冬季为负偏差,冬、夏季偏差相反,西欧地区也是相同的变化规律。对于东亚地区,夏季误差较小,而冬季为明显的负偏差,上述分析表明,不同地区在不同季节有不同的预报误差特征。
|
图 3 不同季节500 hPa位势高度120小时预报场与分析场的平均误差对比(单位:dagpm) (a) 2009年7-8月, (b) 2010年1-2月 Fig. 3 The 500 hPa geopotential height average bias between 120 h forecast and NCEP analysis for (a) July and August 2009, and (b) Janyary and February 2010 (unit:dagpm) |
综合以上分析可以发现:整体而言,T639模式对这三个要素预报都存在一定的系统误差,且系统误差随着预报时效的增加而增加。但是系统误差随地区差异而不同,并且随季节变化而变化,而“递减平均法”对于不同的时间距离使用递减权重,并且对逐个预报格点进行动态订正,适合订正动态变化的系统误差。
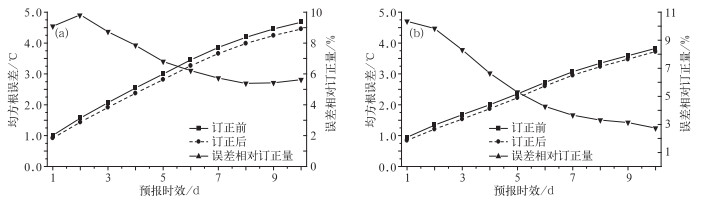
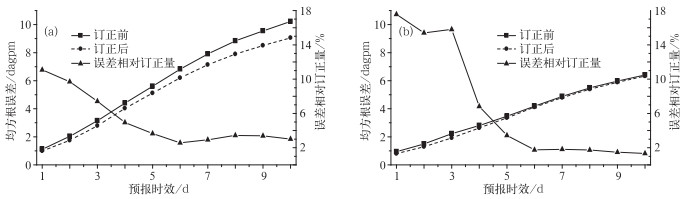
2.2 订正效果检验北半球和东亚地区500 hPa高度预报场订正前后的均方根误差对比分别如图 4所示,其中东亚地区选取的范围为:10°~60°N、70°~150°E(下同)。从图中可以看出,对于北半球和东亚地区,经过“递减平均法”订正后的均方根误差均小于订正前,说明该订正方法总体为正的订正效果,但是订正能力随预报时效增加而下降。对于整个北半球1~3天预报的订正能力在5%以上,而东亚地区在9%以上。而6~10天,该方法对T639模式500 hPa高度预报场误差相对订正量在1%~2%,未通过显著性检验,基本无订正能力。
|
图 4 北半球(a)和东亚地区(b)的500 hPa高度场订正前后均方根误差对比和误差相对订正量 Fig. 4 The RMS and relative correction errors of 500 hPa height before/after correction in the Northern Hemisphere (a) and East Asia (b) (square solid: RMS error before correction; circle dashed: RMS error after correction; triangle solid: relative correction error, right Y axis) |
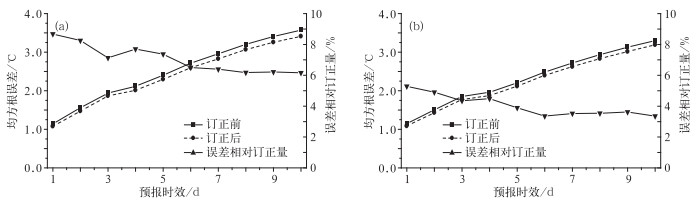
图 5~6分别是850 hPa温度和2 m温度的订正前后对比情况。与500 hPa高度场类似,“递减平均法”对于两者都是正的订正技巧,但随着预报时效的增加订正能力下降较缓慢。对于850 hPa温度(图 5),东亚地区的均方根误差总体小于整个北半球,“递减平均法”的订正能力小于整个北半球,特别是预报时效超过6天之后。对于地面2 m温度(图 6),东亚地区的均方根误差和整个北半球基本一致,但东亚地区的误差相对订正能力都低与北半球,可能原因是东亚地区地形较复杂,误差中的随机误差占的比重更大。
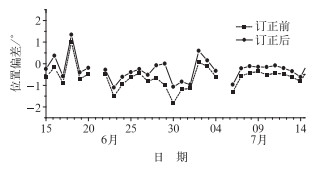
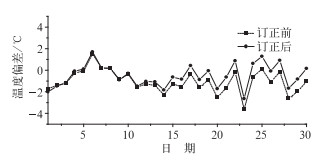
每年6月中旬至7月中旬为江淮地区的主汛期,在此期间,准确预报暴雨落区对于防洪防汛至关重要。任敏等[8]对安徽省暴雨落区和500 hPa高度场统计发现,暴雨区在5840 gpm线附近频数最高,5840线的位置可以作为暴雨落区预报的依据之一。图 7为2009年6月15日至7月15日,120°E经线上500 hPa 48小时预报场中5840 gpm的北界位置订正前后的误差对比。整体而言,订正前T639模式预报的5840线北界位置略偏南,平均偏南0.69个纬度,而订正后的北界位置整体向北移动,订正后的位置平均偏南0.24个纬度,向北订正约0.45个纬度,该方法提高了对5840 gpm线北界位置的预报准确率。图 8为2010年11月地面2 m温度144小时预报场订正前后的误差对比。11月预报的平均误差约为-1.0℃,订正后的平均误差为-0.7℃,订正幅度在0.3℃,误差减少了约30%。对于下半月,整体预报的温度偏低,订正效果更加明显。而对于上半月,由于误差的正负交错出现,对预报场基本无修正,该例子也说明只有当系统误差较明显时,该方法才具有较好的订正能力。
|
图 7 2009年6月15日至7月15日500 hPa位势高度48小时预报场、120°E上5840 gpm的订正前后北界位置误差对比(单位:°) Fig. 7 The bias of 5840 gpm north position before (dashed)/after (solid) correction with 48 h forecast at 120°E from 15 June to 15 July 2009 (unit: °) |
|
图 8 2010年11月地面2 m温度144小时预报场订正前后的误差对比(30°N、115°E) (单位:℃) Fig. 8 The 2 m tempterature bias before (dashed)/after (solid) correction with 144 h forecast at point (30°N, 115°E) for November 2010 (unite: ℃) |
为了检验不同季节“递减平均法”的订正能力,分别统计了夏半年和冬半年的误差相对订正量,其中定义夏半年为4-9月,冬半年为10月至翌年3月。三个要素预报场夏半年和冬半年的误差相对订正量对比情况如图 9所示。对于500 hPa高度(图 9a)和850 hPa温度场(图 9b),夏半年和冬半年的误差相对订正量区别不大,说明其订正能力随季节无明显变化。而对于2 m温度(图 9c),“递减平均法”冬半年的订正能力远大于夏半年。造成这种现象的可能原因是冬半年地面温度变化更剧烈,容易产生系统误差。从其随预报时效变化情况分析:冬半年订正能力随预报时效增加而下降,而夏半年对2 m温度的订正能力变化不大。总之,对于500 hPa高度和850 hPa温度,冬半年和夏半年的订正技巧相当;而对于2 m温度,冬半年订正技巧明显高于夏半年。
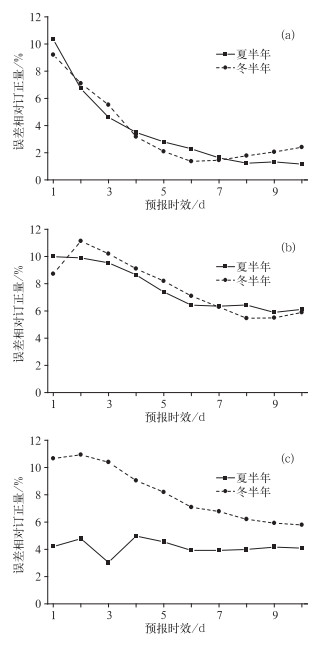
|
图 9 500 hPa位势高度(a)、850 hPa温度(b)和2 m温度(c)冬夏半年误差相对订正量对比 Fig. 9 Relative correction errors of cold and warm season for 500 hPa geopotential height (a), 850 hPa temperature (b), and 2 m temperature (c) (square solid: warm season, circle dashed: cold season) |
权重系数的大小反映了“递减平均法”中历史预报误差的权重大小,直接影响最后的订正结果。图 10为850 hPa温度的误差相对订正量随权重系数的变化图。对于北半球(图 10a),随着权重系数的增加,第1和第3天的订正效果先增加后减小,权重系数取0.08~0.12时,误差订正效果较好。东亚地区(图 10b)的订正效果随权重系数的变化情况和北半球基本一致,当权重系数取0.1附近时具有较好的订正效果。2 m温度场和850 hPa温度场的结论基本一致。而对于500 hPa高度场(图略),其误差相对订正量随着权重系数的增加先增加后减小,当权重系数取0.05~0.08之间时,误差相对订正量达到极大值。综合以上分析,在实际应用中,对于500 hPa高度场,权重系数约取0.06,对于850 hPa温度和地面2 m温度场,权重系数约取0.1时,可以得到较好的订正效果。
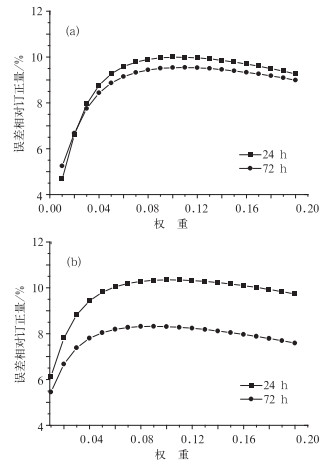
|
图 10 850 hPa温度的误差相对订正量随权重系数的变化图 (a)北半球,(b)东亚地区 Fig. 10 Relative correction errors of 850 hPa temperature versus different weight factors in (a) Northern Hemisphere, and (b) East Asia |
本文统计了2009-2010年T639数值模式500 hPa高度、850 hPa温度和2 m温度的1~10天预报场的系统误差,并尝试利用“递减平均法”对其进行订正,初步得到以下结论:
(1) 对于500 hPa高度、850 hPa温度和2 m温度,T639模式预报都存在一定系统误差,不同要素具有不同的误差空间分布,系统误差具有明显季节变化特征,且随着预报时效的增加而增加。
(2) “递减平均法”总体表现为正的订正技巧,但订正能力随着预报时效的增加而下降,其中500 hPa高度场订正能力下降更迅速,而对温度场的订正能力下降较为缓慢。
(3) 对于东亚区域,T639模式500 hPa高度、850 hPa温度和2 m温度预报场的系统误差都小于整个北半球,“递减平均法”的订正能力总体小于整个北半球,但对于1~3天500 hPa高度预报场订正能力超过10%。
(4) 对于500 hPa位势高度和850 hPa温度预报场,冬半年和夏半年的订正技巧基本相当;而对于2 m温度预报场,冬半年订正技巧明显高于夏半年。
(5) “递减平均法”中不同权重系数试验表明:使用适当的权重系数可以得到最佳的订正效果。对于500 hPa高度场,权重系数约取0.06时,订正效果较好。对于850 hPa和2 m的温度场,权重系数取0.1时,订正效果较好。
目前该统计订正工作只针对500 hPa高度、850 hPa温度和2 m温度预报场,对于其他气象要素预报是否也有正的订正技巧,需要进一步开展相关的工作。另外,目前的预报场为2年的资料,样本长度对结论是否有一定影响,有待进一步验证。
致谢:感谢美国国家环境预报中心(NCEP)的朱跃建博士、崔波博士给予技术指导;对审稿老师针对本文给予的指导和修改,在此一并感谢!
管成功, 陈起英, 佟华, 等, 2008. T639L60全球中期预报系统预报试验和性能评估[J]. 气象, 34(6): 11-16. DOI:10.7519/j.issn.1000-0526.2008.06.002 |
周慧, 崔应杰, 胡江凯, 等, 2010. T639模式对2008年长江流域重大灾害性降水天气过程预报性能的检验分析[J]. 气象, 36(9): 60-67. DOI:10.7519/j.issn.1000-0526.2010.09.010 |
石顺吉, 吴陈锋, 陈德花. 0903号强热带风暴"莲花"数值预报检验[G]. 第26届中国气象学会年会热带气旋科学研讨会分会场论文集, 2009: 101-107.
|
蔡芗宁, 2010. 2009年9—11月T639、ECMWF及日本模式中期预报性能检验[J]. 气象, 36(2): 130-135. DOI:10.7519/j.issn.1000-0526.2010.02.020 |
李莉, 朱跃建, 2006. T213降水预报订正系统的建立与研究[J]. 应用气象学报, 17(增刊): 130-134. |
李莉, 李应林, 田华, 等, 2011. T213全球集合预报系统性误差订正研究[J]. 气象, 37(1): 31-38. DOI:10.7519/j.issn.1000-0526.2011.01.004 |
黄嘉佑, 2004. 气象统计分析与预报方法[M]. 北京: 气象出版社, 20-21.
|
任敏, 陈炎, 璩瑛, 2006. 安徽暴雨落区与一些物理量关系的统计分析[J]. 气象, 32(4): 40-44. DOI:10.7519/j.issn.1000-0526.2006.04.007 |
 2012, Vol. 38
2012, Vol. 38