2. 中国科学院研究生院,北京 100049;
3. 国家海洋环境预报中心,北京 100081;
4. 国家气象中心,北京 100081
2. Graduate University of Chinese Academy of Sciences, Beijing 100049;
3. National Marine Environment Forecast Centre, Beijing 100081;
4. National Meteorological Centre, Beijing 100081
对流尺度天气往往造成严重的自然灾害,而目前利用数值模式对其进行准确预报还是个难点,主要原因是数值模式初始场中高分辨率探测资料的缺乏和在模式中利用该资料技术的不成熟。多普勒雷达资料具有高时空分辨率的特点,用它来改进数值模式初始场,对提高对流尺度灾害性天气预报的准确率有重要意义。
由于多普勒雷达观测数据不是常规气象要素,其在数值模式中的应用需要从探测的径向风和反射率来估计实际大气的状态,得到风、温、压、湿等模式变量场。目前同化雷达资料的方法主要有反演类算法[1-2]、热动力初始化方法[3-5]、松弛逼近方法[6]、变分类方法[7-12],以及集合卡尔曼滤波(EnKF)方法。集合卡尔曼滤波同化方法利用一组预报集合来估计背景场误差协方差,自Evensen[13]1994年首次引入到地球物理领域,EnKF以其流依赖的背景场误差协方差、模式和观测算子可为非线性、不需要切线性伴随、易于并行等诸多优点,已经在多种大气和海洋模式中得到了广泛应用,成为目前最具业务发展前景的同化方法之一。近年来,在对流尺度系统中的应用EnKF方法同化雷达资料的研究取得了较大进展,Snyder等[14]首次将EnKF用于对流尺度系统实施同化雷达资料的观测系统模拟试验,他们采用Sun等[15]发展的暖云模式同化了模拟的单多普勒雷达径向风观测,初步验证了EnKF在对流尺度的同化效果。Dowell等[16]在相同的暖云模式中尝试了真实的单多普勒雷达反射率和径向风资料的同化,并将结果与观测做了对比,结果表明风场的反演效果较好,温度场由于模式误差和观测的限制没有得到很好的反演。许小永等[17]也采用此暖云模式同化了模拟的雷达观测和一次梅雨锋暴雨过程的双多普勒雷达资料,试验表明EnKF同化技术能够从雷达资料较准确地反演暴雨中尺度系统的动力场、热力场和微物理量场。Tong等[18-19]将此领域的研究推进到包含冰相微物理过程的同化,他们在ARPS模式中同化了模拟的雷达反射率和径向风,得到了对风暴流场、热力场和各种微物理量场的准确分析。Zhang等[20]将EnKF同化系统应用于实际雷达资料同化,针对一次台风过程在WRF模式中同化了径向风观测,并进行了确定性预报和集合预报,试验表明,径向风同化能较好地分析出台风路径和强度,并有能力预报台风的快速形成和突然增强。
以上研究初步显示了EnKF同化方法在对流尺度的应用前景,但其针对雷达资料的同化技术不够成熟,目前国内这方面的研究也比较少,还需要开展进一步的研究工作。本文基于WRF模式,利用EnKF系统进行了同化雷达资料的观测系统模拟试验,并结合试验结果对EnKF雷达资料同化系统的性质进行了探讨和分析,以期获得对此同化系统更深入的认识,并为多普勒雷达资料在数值模式中的同化应用提供一些借鉴和科学依据。
1 同化系统及试验设计 1.1 预报模式预报模式采用完全可压的欧拉非静力中尺度WRF模式,包含6个预报方程和一个静力诊断方程,预报变量为三维风场、扰动位温、扰动位势、干空气地面扰动气压,以及水汽、云水、雨水、冰晶、雪和霰的混合比等可选择的预报变量。
试验采用WRF模式中超级单体理想试验方案,积分区域格点数为42×42×41,水平格距2 km,垂直方向0.5 km,雷达天线位于(0,0,0),即模式区域底部的西南角。积分时间步长为12秒,微物理过程选用WSM6方案,包含了5种水凝物的混合比,使用开放式侧边界条件。
1.2 同化分析系统 1.2.1 集合卡尔曼滤波分析WRF-EnKF同化系统由奥克拉荷马大学风暴分析与预报中心提供,与Tong等[18]相似,不同之处为本文的同化系统基于不扰动观测的集合方根卡尔曼滤波方法,即EnSRF方法,分析场为平均分析场xa与扰动分析场x′a的和:
| $ x_k^a = {{\bar x}^a} + {{x'}_k}^a $ | (1) |
| $ {{\bar x}^a} = {{\bar x}^f} + K\left( {{y^o} - H{{\bar x}^f}} \right) $ | (2) |
| $ {{x'}_k}^a = \gamma \left( {I - \mu KH} \right){{x'}_k}^f $ | (3) |
| $ K = P_k^f{H^{\rm{T}}}{\left( {HP_k^f{H^{\rm{T}}} + {R_k}} \right)^{ - 1}} $ | (4) |
式中,上标a和f分别表示分析场和预报场,下标k表示第k个同化时步,K为卡尔曼增益矩阵,yo为同化的观测,Pf为背景场误差协方差,R为观测误差协方差,H为观测算子,γ为协方差扩大因子,一般略大于1。
| $ \mu = {\left( {1 + \sqrt {\frac{R}{{H{P^f}{H^{\rm{T}}} + R}}} } \right)^{ - 1}} $ | (5) |
在观测误差独立且与背景场误差不相关的假设下,同化观测的先后顺序不影响同化结果,逐个顺序同化观测,这时HPfHT和R都成为标量。
背景场误差协方差由预报集合估计得到,k时步的背景场误差协方差矩阵通过以下式子得到:
| $ {P^f}{H^{\rm{T}}} = \frac{1}{{N - 1}}\sum\limits_{k = 1}^N {\left( {x_k^f - {{\bar x}^f}} \right)} {\left[{H\left( {x_k^f} \right)-\overline {H\left( {{x^f}} \right)} } \right]^{\rm{T}}} $ | (6) |
| $ \begin{array}{l} H{P^f}{H^{\rm{T}}} = \frac{1}{{N - 1}}\sum\limits_{k = 1}^N {\left[{H\left( {x_k^f} \right)-\overline {H\left( {{x^f}} \right)} } \right]} \left[{H\left( {x_k^f} \right)} \right.-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {\overline {H\left( {{x^f}} \right)} } \right]^{\rm{T}}} \end{array} $ | (7) |
式中,N为集合成员数。
1.2.2 观测算子同化的观测包括雷达径向风和反射率因子,试验中假设观测误差间不相关,观测误差满足高斯分布。EnKF中允许非线性观测算子的直接使用而无需线性化,本文雷达反射率的观测算子是非线性的。
雷达径向风的观测算子为:
| $ {V_r} = u\cos \alpha \sin \beta + v\cos \alpha \cos \beta + w\sin \alpha $ | (8) |
式中,Vr为雷达径向风观测,α为雷达波束的仰角,β为雷达波束的方位角,u、v、w为模式输出的风分量。
雷达反射率因子的观测算子为:
| $ Z = 10{\log _{10}}\left( {\frac{{{Z_e}}}{{1\;\;{\rm{m}}{{\rm{m}}^6} \cdot {{\rm{m}}^{ - 3}}}}} \right) $ | (9) |
式中,Z和Ze分别是以dBz和mm6·m-3为单位的雷达反射率因子,
| $ Z\left( {{\rm{dBz}}} \right) = 10{\log _{10}}\left( {\frac{{{Z_e}\;{\rm{m}}{{\rm{m}}^6} \cdot {{\rm{m}}^{ - 3}}}}{{1\;\;{\rm{m}}{{\rm{m}}^6} \cdot {{\rm{m}}^{ - 3}}}}} \right) $ | (10) |
总的雷达反射率因子由雨、雪、雹的反射率因子Zer、Zes、Zeh加和得到。
| $ {Z_e} = {Z_{er}} + {Z_{es}} + {Z_{eh}} $ | (11) |
各水凝物反射率因子的计算基于Smith等[21]和Lin等[22]的算法求得,其中,雨滴的反射率因子为:
| $ {Z_{er}} = \frac{{{{10}^{18}} \times 720{{\left( {\rho {q_r}} \right)}^{1.75}}}}{{{{\rm{ \mathsf{ π} }}^{1.75}}N_r^{0.75}\rho _r^{1.75}}} $ | (12) |
温度低于0°时,干雪的反射率因子为:
| $ {Z_{es}} = \frac{{{{10}^{18}} \times 720K_i^2 \times \rho _s^{0.25}{{\left( {\rho {q_s}} \right)}^{1.75}}}}{{{{\rm{ \mathsf{ π} }}^{1.75}}K_r^2N_r^{0.75}\rho _i^2}} $ | (13) |
温度高于0°时,湿雪的反射率因子为:
| $ {Z_{es}} = \frac{{{{10}^{18}} \times 720{{\left( {\rho {q_s}} \right)}^{1.75}}}}{{{{\rm{\pi }}^{1.75}}N_s^{0.75}\rho _s^{1.75}}} $ | (14) |
雹的反射率因子:
| $ {Z_{eh}} = {\left( {\frac{{{{10}^{18}} \times 720}}{{{{\rm{ \mathsf{ π} }}^{1.75}}N_h^{0.75}\rho _h^{1.75}}}} \right)^{0.95}}{\left( {\rho \;{q_h}} \right)^{1.6625}} $ | (15) |
式中,ρ为空气密度,ρr=1000 kg·m-3,为雨水密度,ρs=100 kg·m-3,为雪的密度,ρi=917 kg·m-3,为冰晶的密度,ρh=913 kg·m-3,为雹的密度;qr、qs、qh分别为雨、雪、雹的比含水量;Nr=8.0×10-6 m-4,Ns=3.0×10-6 m-4、Nh=4.0×10-6 ·m-4分别为雨、雪、雹的Marshall-Palmer指数型滴谱分布的截断参数,Ki2=0.176、Kr2=0.93分别为冰晶和雨滴的介电系数。
1.2.3 协方差局地化由有限集合样本数引入的样本误差会导致背景场误差协方差的估计误差,尤其会在观测较远处产生虚假的分析增量。Houtekamer等[23]提出了Schur乘积方法解决这个问题,使用Schur乘积后卡尔曼增益变为:
| $ K = \left[{\rho \circ \left( {{P^f}{H^{\rm{T}}}} \right)} \right]{\left[{\rho \circ \left( {H{P^f}{H^{\rm{T}}}} \right) + R} \right]^{ - 1}} $ | (16) |
系统中采用了此算法,并使用Gaspari等[24]的5阶分段有理函数来定义局地相关函数。5阶分段有理函数的形式为:
| $ \rho \left( {r, c} \right) = \left\{ \begin{array}{l} - \frac{1}{4}{\left( {\frac{r}{c}} \right)^5} + \frac{1}{2}{\left( {\frac{r}{c}} \right)^4} + \frac{5}{8}{\left( {\frac{r}{c}} \right)^3} - \frac{5}{3}{\left( {\frac{r}{c}} \right)^2} + 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \le r \le c\\ \frac{1}{{12}}{\left( {\frac{r}{c}} \right)^5} - \frac{1}{2}{\left( {\frac{r}{c}} \right)^4} + \frac{5}{8}{\left( {\frac{r}{c}} \right)^3} + \frac{5}{3}{\left( {\frac{r}{c}} \right)^2} - 5\left( {\frac{r}{c}} \right) + 4 - \frac{2}{3}{\left( {\frac{r}{c}} \right)^{ - 1}} + 1\;\;\;\;c \le r \le 2c\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2c \le r \end{array} \right. $ | (17) |
式中,r为观测与背景场上分析格点之间的距离,c为给定的长度尺度参数。
| $ r = \sqrt {r_x^2 + r_y^2 + r_z^2} $ | (18) |
集合的离散度应该代表集合平均场的误差统计特征,然而有限集合数带来的样本误差会造成集合离散度与集合平均场误差的不一致,从而导致滤波发散。离散度过小会导致EnKF分析不吸收观测,而离散度过大则会使分析过度偏离背景场。集合离散度与集合平均场误差在统计上满足如下一致性关系[25]:
| $ \frac{{E\left[{\frac{1}{{{N_e}-1}}\sum\limits_{n = 1}^{{N_e}} {{{\left| {x_n^f-{{\widehat x}^f}} \right|}^2}} } \right]}}{{E\left( {{{\left| {{x^t} - {{\widehat x}^f}} \right|}^2}} \right)}} = \frac{{{N_e}}}{{{N_e} + 1}} $ | (19) |
式中Ne为集合成员数。协方差调节是解决滤波发散问题的有效方法,即式(3) 中给扰动分析场乘以一个扩大因子β来调节集合成员的发散度,从而缓解滤波发散问题。
1.3 试验设计设计了真值模拟试验、控制试验和同化试验三组试验,试验流程见图 1。
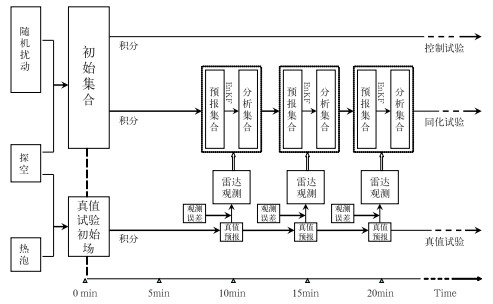
|
图 1 WRF-EnKF雷达资料同化试验流程示意图 Fig. 1 Flow chart of radar data assimilation experiment based on WRF-EnKF |
假设模式完美,在不考虑模式误差的影响下可将模拟结果当成大气真实状态,与同化试验结果进行对比以检验同化效果。真值试验积分开始时刻在探空环境场中植入一高于环境场3 K的椭圆热泡以激发对流,热泡中心在x=41 km,y=41 km,z=1.5 km处,其水平影响半径为10 km,垂直影响半径为1.5 km,热泡以外θ为水平均匀场。
真值实验探空如图 2所示,取自于WRF模式超级单体理想试验,其CAPE值为2301 J·kg-1,CIN值为16 J,LI指数为-8,为避免右移风暴离开模拟区域中心,将探空的纬向风减去了6 m·s-1。
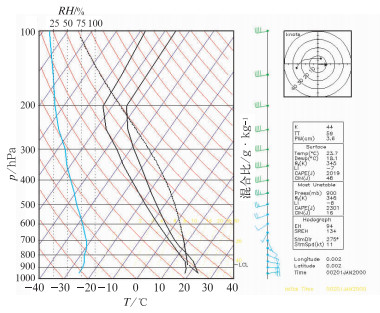
|
图 2 探空斜温图 Fig. 2 Skew T diagram for the environmental sounding |
真值模拟中,液相水凝物约于5~10 min时在900~500 hPa开始生成,冰相水凝物约于10~15 min时在650~300 hPa生成,垂直上升气流在70 min达47 m·s-1。约40 min单体开始分裂,分别向南北方向移动,北边的单体在90 min左右分裂为两个,之后不断分裂减弱,南边的单体逐渐成为主导单体,于145 min后逐渐移出模拟区域。
1.3.2 同化试验同化试验的初始集合由环境场叠加初始扰动得到,环境场为由探空资料提供的水平均匀场,初始场各层w=0。初始扰动采用高斯分布的随机扰动,u、v、w的均方差都取为3 m·s-1,θ的均方差取1 K。集合成员取20个,从t=0 min开始积分,10 min后进行第一次集合卡尔曼滤波分析,之后每5 min进行一次同化分析,共做20个同化循环。同化的观测为模拟的雷达径向风和雷达反射率因子,径向风和反射率因子观测由下式得到:
| $ {V_r} = V_r^t + {\varepsilon _{{V_r}}} $ | (20) |
| $ {Z_r} = {Z^t} + {\varepsilon _z} $ | (21) |
其中,Vrt和Zt分别为雷达径向风和反射率观测的真值,从观测算子计算得到,εVr和εZ分别为雷达径向风和反射率的观测误差,假设观测误差分布为高斯型,其均方差分别为1 m·s-1和5 dB。分析变量为三维风场、扰动位温、水汽混合比以及水汽、云水、雨水、云冰、雪、雹5种水凝物的混合比。
1.3.3 控制试验为与同化试验结果做对比,设计了不进行同化的集合预报作为控制试验,初始集合与同化试验一样,集合成员也取20个,从t=0 min开始做集合预报,预报120 min,不同化雷达观测。
2 试验结果 2.1 对集合平均分析场的分析能力图 3将5 km高度上20、60和100 min的同化后集合平均分析场与真值场及控制试验集合平均场做了比较。由图可见,风暴附近的中层水平风分析场在3个同化循环后就能较准确地反映真值场的流型,垂直上升、下沉运动的位置与真值场吻合,但强度上稍微偏弱,风暴附近扰动位温的高值区也与真值吻合较好。60 min,垂直上升运动的强度仍稍偏弱,但水平流场和扰动位温都与真值场非常一致。11个同化循环后,流场和扰动位温场与真值场基本完全吻合。而控制试验中,风暴一直没发展起来,各变量场的大小和空间分布从开始到结束几乎没有变化,与真值场相差甚远。
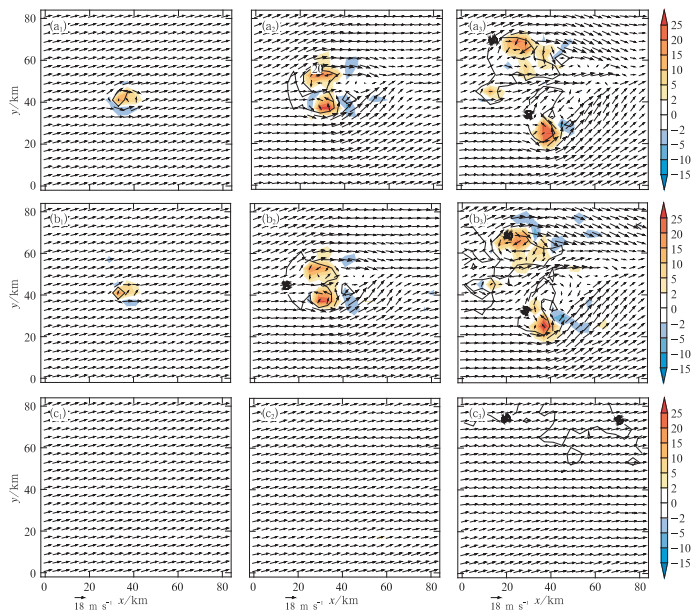
|
图 3 5 km高度上真值场(第一行,a)、同化试验集合平均分析场(第二行,b)和控制试验集合平均场(第三行,c)在20 (a1,b1,c1)、60 (a2,b2,c2)、100 (a3,b3,c3)min时垂直速度场(阴影区)、水平速度场(矢量图)和扰动位温的分布 Fig. 3 Vertical velocity (shaded), horizontal wind (vector) and perturbed potential temperature (contours) at 5 km in the truth simulation (top row), the EnKF anaysis (ensemble mean, middle row) and the control run (ensemble mean, bottom row) which are shown at t=20 min (left panel), 60 min (middle panel), 100 min (right panel) |
对真值模拟、同化试验和控制试验沿风暴中心剖面的水汽扰动和各水凝物混合比做了比较,可见在3个同化循环后,水汽和微物理量场的位置与真值场吻合得很好,量上略微偏弱。5个同化循环后EnKF对水汽和微物理量场的细致特征也能准确刻画。
下面通过误差分析来检验同化分析对热力场、流场、水凝物场的分析和反演能力,采用均方根误差作为指标进行分析。集合平均预报误差rmsf和集合平均分析误差rmsa由式(22) 和(23) 计算:
| $ {\rm{rm}}{{\rm{s}}_f} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {\bar X_i^f - {X^t}} \right)}^2}} } $ | (22) |
| $ {\rm{rm}}{{\rm{s}}_a} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {\bar X_i^a - {X^t}} \right)}^2}} } $ | (23) |
N为全场或雨区的总格点数,Xif为集合平均预报场,xia为集合平均分析场,Xt为真值场。
图 6给出了控制试验预报误差和同化试验的集合平均场各主要变量的均方根误差分布。由图可见,控制试验预报误差增长很快,误差值也很大,而经过同化循环后,所有变量的预报误差和分析误差都比控制试验显著减小,并且基本上在每次同化分析之后,都比预报场误差有所下降,说明同化分析对预报有显著改进。
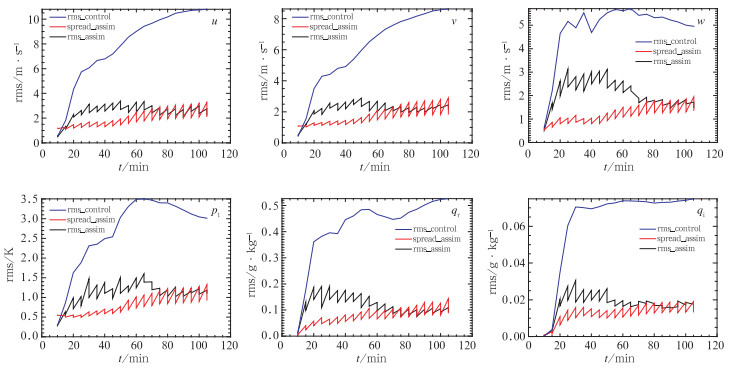
|
图 6 控制试验预报误差和同化试验的集合平均场各变量的均方根误差(包括预报误差和分析误差),以及同化试验中的集合成员发散度(蓝线表示控制试验误差,黑线表示同化试验误差,红线表示同化试验中成员的集合发散度) Fig. 6 The rms errors of variables (u, v, w, pt, qr, qi) of ensemble mean forecast and analysis from EnKF (black) and of control run (blue), ensemble spread of EnKF (red) |
风场预报误差在头两个循环迅速增大,20~55 min预报和分析误差增长缓慢,之后误差略有下降并在震荡中逐渐收敛,u、v、w的分析误差分别收敛至约2.5、2和1.5 m·s-1左右。流场在第一个循环预报集合误差很小,主要是由于同化前初始集合经过了一段时间积分,使得预报场与真值场差别不大。温度扰动场(pt)、云水(qr)、云冰(qi)等水凝物也有误差在开始两三个循环增加,之后趋于平稳,最后逐渐收敛的特点。
|
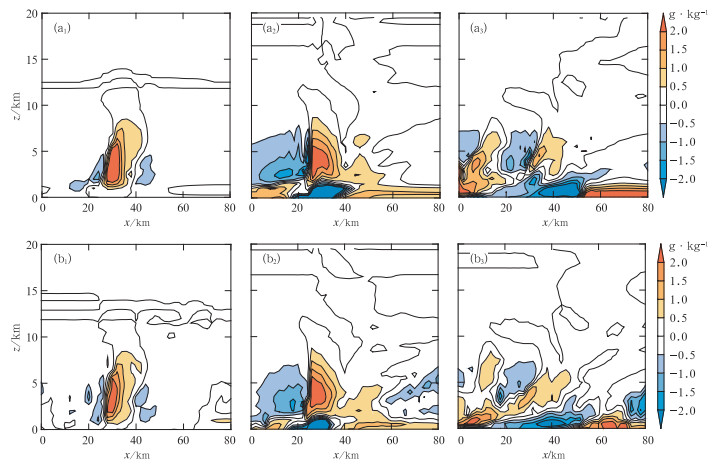
图 4 真值场(a)和同化试验集合平均分析场(b)的扰动水汽混合比q′v在20(a1,b2)、60(a2,b2)和100(a3,b3) min沿y=41 km的x-z剖面图 Fig. 4 Perturbation q′v of truth simulation (top row) and EnKF analysis (bottom row) in the x-z plane at y=41 km at 20 min (left panel), 60 min (middle panel), 100 min (right panel) |
|
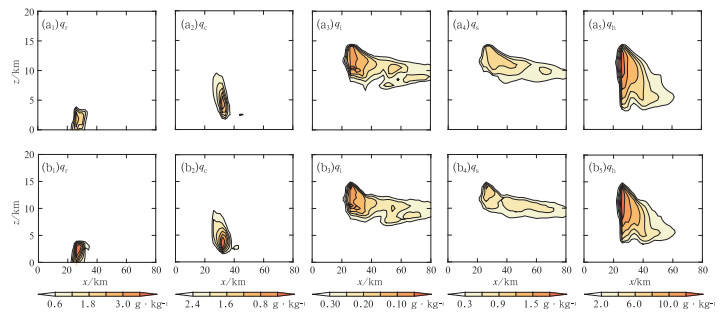
图 5 真值场(a)和同化试验(b)的集合平均分析场中各水凝物(从左至右依次为雨水qr、云水qc、冰晶qi、雪qs及雹qh的混合比)在60 min沿y=41 km的x-z剖面图 Fig. 5 qr, qc, qi, qs and qh of truth simulation (a) and EnKF analysis (b, emsemble mean) in the x-z plane at y=41 km at 60 min |
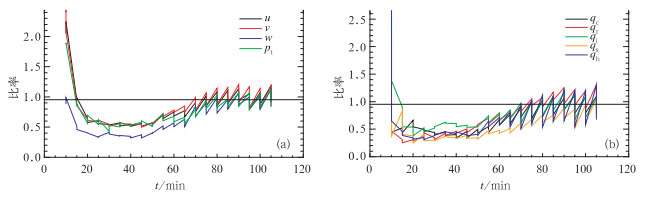
同化初期各变量场预报误差迅速增加,主要是由于这段时间风暴发展迅速,流场、热力场及水凝物场的迅速变化使得同化后分析场的强度跟不上风暴的发展而造成;同化初期分析场的误差下降不明显主要是因为同化开始阶段观测和模式变量间合理的协相关关系还没有建立起来,此时分析还不能准确更正模式变量的预报误差,但几个循环之后,分析对预报场的更正明显增强,说明3~4个同化循环之后,观测与模式变量场之间的协相关关系开始趋于合理,观测信息逐渐能对预报场进行准确的调整,60 min之后,可靠和协调的背景场误差协方差基本建立起来,误差逐渐收敛。如图 7所示,60~70 min之后集合离散度/集合平均场误差比率在Ne/(Ne+1) 附近振荡[参考本文式(19)],这时集合的发散度对集合平均场的误差统计特征有很好的代表性,EnKF分析在这时准确可靠。
|
图 7 集合离散度与集合平均场误差的比率[黑色直线为Ne/(Ne+1] Fig. 7 Ratio of the ensemble variance to the squrared error of the ensemble mean, the horizontal line indicates Ne/(Ne+1) |
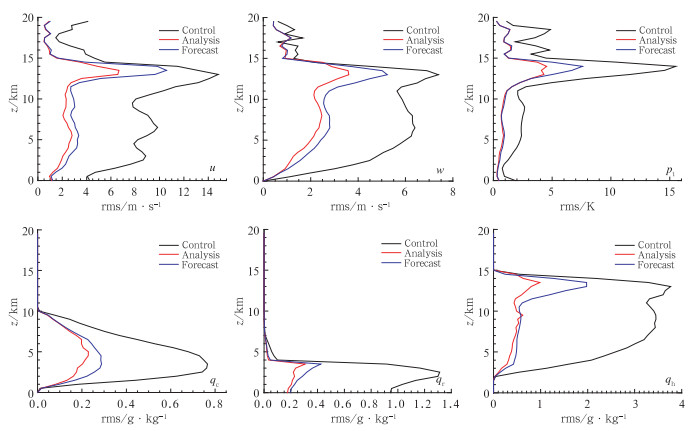
从图 8各变量误差的垂直分布可见,误差值一般在该变量发展较强的高度较大,在同化初始时刻误差大值区的高度较低,值也较小,随着对流风暴逐渐向高层发展,误差大值区逐渐向上移动,值也迅速变大,各变量误差大值高度基本代表了该变量发展最旺盛的高度。60 min时流场误差最大值高度发展到约15 km;水汽在低层较大,其误差大值区始终在10 km以下,45 min后误差的最大值一直在1 km以下;水凝物的误差只在含有这种水凝物的高度上有值,其他层次上误差值为零。
|
图 8 控制试验预报误差和同化试验集合平均场各变量在60 min的水平均方根误差的垂直廓线(蓝线、红线、黑线分别表示同化试验预报误差、分析误差和控制试验预报误差) Fig. 8 Vertical profiles of rms errors of EnKF forecast (blue), EnKF analysis (red) and control run (black) at 60 min |
综合各变量来看,在误差较大的层次,分析对预报场的更正非常明显,在误差较小的高层和低层分析对预报的更正很小或几乎为零。由图也可见,同化试验误差始终小于控制试验误差,分析对预报场的改进在同化的前期和中期比较显著,在误差较大的层次比较显著。而控制试验的误差从高层到低层都大于同化试验的预报误差,在误差较大的层次,控制试验的误差更大。
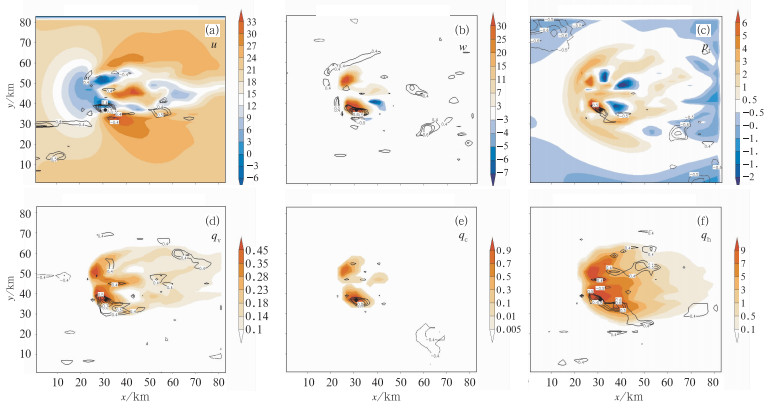
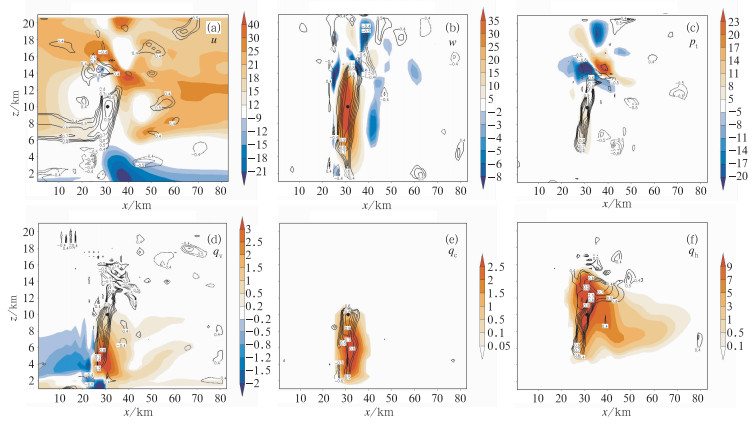
2.2 背景场误差协方差分析由预报集合估计的流依赖的背景场误差协方差在EnKF的变量分析中扮演着非常重要的角色。背景场误差协方差包含两部分内容:相关和方差,方差大值区一般对应于系统发展剧烈的区域,相关系数则表示了某点上某变量的增量对其他点某变量变化的影响程度。图 9和10为60 min时点(16,19,19)(为上升运动强中心,图中粗黑点标出)与z=19水平面及y=19剖面上各点上流场,温度场,水汽场、水凝物场同变量间的背景场误差的水平(图 9)和垂直(图 10)相关系数。
|
图 9 60 min时点(16,19,19) 与z=19(9 km)水平面上各点同变量(依次为:u、w、pt、qv、qc、qh)间的背景场误差水平相关系数,填色图为此变量的真值场 Fig. 9 Background error correlations estimated from an ensemble at 60 min in the x-y plane along z=9 km |
|
图 10 60 min时点(16,19,19) 与y=19(37 km)剖面上各点同变量(依次为:u、w、pt、qv、qc、qh)间的背景场误差垂直相关系数,填色图为此变量的真值场 Fig. 10 Background error correlations estimated from an ensemble at 60 min in the x-z plane along y=37 km |
60 min时,预报场各变量的背景场误相关系数不论在水平方向还是垂直方向都与三维变分方法假定的背景场误差协方差高斯型分布有些相似,基本上有与自身相关系数为1,离目标点越远相关越小的趋势。同时,由图清楚可见背景场误差相关系数有着复杂的结构,与三维变分方法所假定的同心圆结构不同,它是高度非均匀、各项异性和流依赖的。
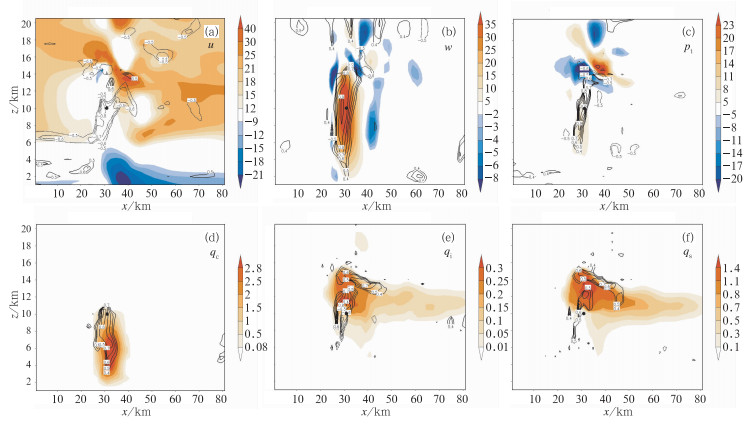
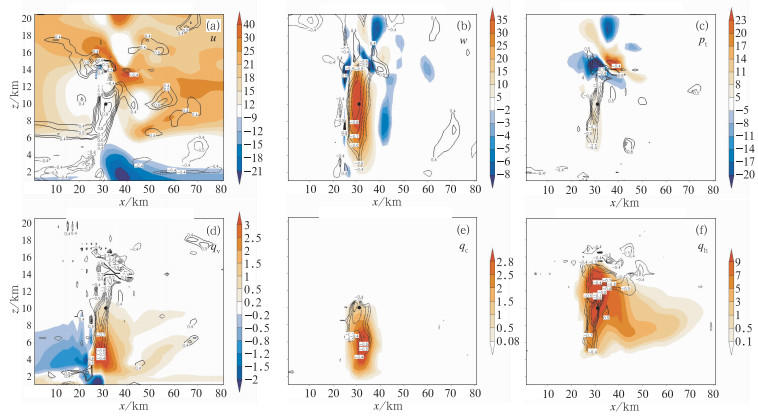
集合卡尔曼滤波雷达资料同化分析的准确性主要依赖于非模式变量的径向风、反射率观测与模式变量间正确协相关关系的建立。图 11和12分别给出了南边单体上升气流中心所在位置,即点(16,19,19) 上的背景场反射率观测和径向风观测与y=19剖面上各点各变量的背景场误差相关系数。
|
图 11 60 min时预报集合的雷达反射率因子与沿y=19(37 km)剖面的各分析变量的背景场误差相关图(等值线,实线为正相关,虚线为负相关),粗黑点为反射率观测所在位置,填色图为此时的真值场各变量,变量依次为:u、w、pt、qc、qi、qs Fig. 11 Background error correlations estimated from an ensemble at 60 min in the x-z plane along y=37 km between reflectivity (indicated by a black dot) and u, w, pt, qc, qi, qs, respectively, thick solid (dashed) contours represent positive (negative) correlations |
|
图 12 60 min时预报集合的雷达径向风与沿y=19(37 km)剖面的各分析变量的背景场误差相关图(等值线,实线为正相关,虚线为负相关),粗黑点为反射率观测所在位置(16,19,19),填色图为此时的真值场各变量(各变量依次为:u、w、pt、qv、qc、qh) Fig. 12 Background error correlations estimated from an ensemble at 60 min in the x-z plane along y=37 km between radial velocity (indicated by a black dot) and u、w、pt、qv、qc、qh, respectively, thick solid (dashed) contours represent positive (negative) correlations |
由图 11可见,60 min时背景场的反射率观测与各模式变量建立的相关关系较好地反映了真值场各变量的结构,结合此时的真值场可以得到,与5种水凝物场和水汽场的相关,正相关大值区很好地对应着此时真值场此变量的大值区域,这是合理的,反射率增量增加了水凝物和水汽,应该对应于对水凝物分析和水汽分析的增加;对于与垂直速度的相关,正相关的高值区较好地对应了垂直上升运动的大值区域,它反映了垂直上升运动带来水汽凝结而对应的反射率增大;对于扰动位势,正相关的高值区对应于真值场扰动位势的大值区,强的上升运动可以带来扰动位势的增大,而强上升运动也对应着水汽的凝结和大的反射率值。由图可以看到,qc、qh、qv、θ、w等变量与雷达反射率是高度相关的,其与反射率相关的最大值都超过了0.9。
由图 12可见,60 min时点(16,19,19) 上的径向风观测与各模式变量间也建立了可靠的相关关系。其中与水平风u和v有很强的正相关(v分量图略),其最大相关值分别超过了0.9和0.8,并且呈近似高斯型的分布,与u风的强相关区位于上升气流区所对应的弱水平气流区;径向风与w在上升气流中心有强的负相关,径向风与上升气流区所对应的正扰动位温区域有较强的负相关,而与上升气流顶部的负扰动位温区有较强的正相关。径向风与扰动位势在扰动位势的高值区有较强的负相关。径向风与5种水凝物和扰动水汽场也都有较强的负相关,其负相关的高值区都对应着这些物理量的大值区。
反射率、径向风观测与各变量的相关图也很好地反映了观测与各模式各变量间相关关系的复杂结构,它是高度非均匀、各项异性和流依赖的。
3 集合平均分析场做的确定性预报为分析同化对其后确定性预报的影响,这一节使用40、50和60 min的集合平均分析场做确定性预报,都报到160 min,检验其预报误差增长情况。
图 13给出了用50 min的集合平均分析场做的确定性预报与真值场在不同时刻的流场和总水凝物场的变化图。用集合平均分析场做的前20多分钟预报较好地保持了真值场风暴的细节结构,包括水平流场的流型、大小,总水凝物的强度、位置,垂直上升运动的结构和位置。75 min开始北边单体上升气流的强度稍微偏弱,总水凝物场的结构与真实风暴也发生了一些差异,尤其在中层,北边单体总水凝物场的强度偏大,南边单体总水凝物的位置较真实风暴偏北,量也偏大,两单体间的水平气流也较真值场偏弱。90 min时,平均分析场的预报场北边的单体在中层(约7 km)开始分裂,并产生其后方大片的虚假水凝物,随后此虚假单体发展迅速,至110 min时在高层(约10 km)与原单体强度相当,而原单体不断减弱,至120 min基本将原单体取代。150 min时,真实单体已逐渐开始移出模拟区域,平均分析场预报的单体向南的移速偏慢,直到160 min左右才逐渐移出模拟区域。
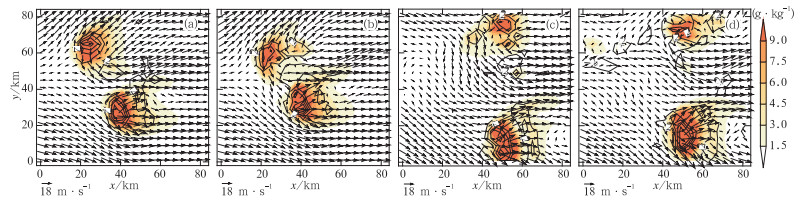
|
图 13 50 min的集合平均分析场做的确定性预报(b,d)与真值场(a,c)在10 km高度上100 min(a,b)和150 min(c,d)的水平风场(矢量)、垂直速度(等值线)、总水凝物场(填色) Fig. 13 Horizontal wind (vector), vertical velocity (contours) and total hydrometeor (shading) of 100 min (a, b) and 150 min (c, d) at 10 km level for the truth simulation (a, c) and the forecast (b, d) beginning from the ensemble mean analysis at 50 min |
从上面的分析可见,预报误差主要来自于虚假的分裂单体,单体的传播速度与真实单体不一致也是误差的来源之一。在开始的10~20 min,预报单体基本能保持实际单体的结构、位置和强度,但预报误差增长很快,预报单体很快与真实单体出现较大差异。预报误差的迅速增长,一方面可能与高度非线性的对流风暴系统发展迅速、预报时效短有关,小误差经过模式积分后误差的非线性增长非常迅速,另一方面也与作为预报初始场的集合平均分析场的误差有关系。
图 14给出了用40、50和60 min的集合平均分析场做确定性预报,报到160 min时各变量的预报误差。由图可见,预报误差随时间的增加都逐渐增长,垂直速度,云、雪、雹比含水量在110~140 min基本达到最大值,之后有减小趋势;60 min时,可信的背景场误差协方差基本建立,用此时的集合平均分析场做的确定性预报误差更小。
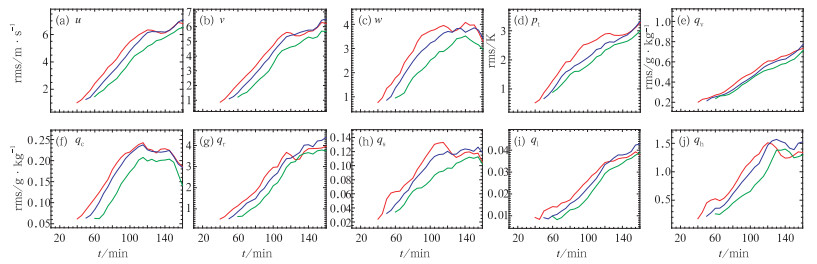
|
图 14 40 min(红线)、50 min(蓝线)和60 min(绿线)的集合平均分析场做的确定性预报的各变量预报误差 Fig. 14 The rms errors of variables of the forecasts begin from ensemble mean analysis at 40 min (red), 50 min (blue) and 60 min (green) |
本文实施了EnKF同化模拟雷达资料的观测系统模拟试验,验证了WRF-EnKF雷达资料同化系统的同化效果,得到结论如下:
(1) WRF-EnKF雷达资料同化系统有能力准确分析模式风暴的风场、热力场、微物理量场的细致特征。试验中EnKF在约3个同化循环后就能比较准确地重建模式风暴,更多的同化循环后,各变量分析场的位置、结构、量级都与真值场非常一致。
(2) 预报误差在每次同化分析后都有所下降,试验中所有变量的预报和分析误差在经过同化循环后都显著减小;各变量预报、分析误差最大的高度都对应该变量发展最旺盛的高度,同化分析基本上能使预报场在各层上都有所改进,对预报场误差较大的层次的更正更为显著。
(3) 背景场误差协方差在EnKF分析中扮演着重要角色,试验表明,约8个同化循环后,EnKF能在雷达反射率、径向风观测与背景场间建立较可靠的相关关系,使模式各变量场能被准确分析更新,背景场误差协方差在水平方向和垂直方向都有着复杂的结构,是高度非均匀、各项异性和流依赖的。
(4) 用集合平均分析场做的确定性预报显示,在短时间内(约30 min)预报能较好地保持真值场风暴的细节结构,但预报误差增长很快,预报误差主要来自于虚假的分裂单体和单体传播速度与真实单体的不一致。误差的迅速增长,一方面可能与非线性的对流风暴系统发展迅速、预报时效短有关,另一方面也与作为预报初始场的集合平均分析场的误差有关系。
Gal-Chen T, 1978. A method for the initialization of the anelastic equations:Implications for matching models with observations[J]. Mon Wea Rev, 106: 587-602. DOI:10.1175/1520-0493(1978)106<0587:AMFTIO>2.0.CO;2 |
Hane C E, Ray P S, 1985. Pressure and buoyancy fields derived from Doppler radar data in a tornadic thunderstorm[J]. J Atmos Sci, 42: 18-35. DOI:10.1175/1520-0469(1985)042<0018:PABFDF>2.0.CO;2 |
Lin Y, Ray P S, Johnson K W, 1993. Initialization of a modeled convective storm using Doppler radar-derived fields[J]. Mon Wea Rev, 121: 2757-2775. DOI:10.1175/1520-0493(1993)121<2757:IOAMCS>2.0.CO;2 |
Xue M, Wang D, Hou D, et al. Prediction of the 7 May 1995 squall line over the central U.S. with intermittent data assimilation[R]. 12th Conference on Numerical Weather Prediction, 1998, 191-194.
|
Zhang J, Carr F, Brewster K. ADAS Cloud Analysis[R]. 12th Conference on Numerical Weather Prediction, 1998, 185-188.
|
Jones C D, Macpherson B, 1997. A latent heat nudging scheme for the assimilation of precipitation data into an operational mesoscale model[J]. Meteor Appl, 4: 269-277. DOI:10.1017/S1350482797000522 |
杨毅, 邱崇践, 龚建东, 等, 2008. 利用3维变分方法同化多普勒天气雷达资料的试验研究[J]. 气象科学, 28(2): 124-132. |
Sun J, Crook N A, 1997. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint: Part Ⅰ. Model development and simulated data experiments[J]. J Atmos Sci, 54: 1642-1661. DOI:10.1175/1520-0469(1997)054<1642:DAMRFD>2.0.CO;2 |
李媛, 刘健文, 董佩明, 等, 2011. GRAPES-3Dvar雷达资料直接同化对江淮暴雨数值预报影响的分析研究[J]. 气象, 37(4): 403-411. DOI:10.7519/j.issn.1000-0526.2011.04.003 |
许小永, 郑国光, 刘黎平, 2004. 多普勒雷达资料4DVAR同化反演的模拟研究[J]. 气象学报, 62(4): 410-422. DOI:10.11676/qxxb2004.042 |
杨艳蓉, 王振会, 杨洪平, 等, 2008. 多普勒雷达反射率与径向风资料在数值模式中的应用试验[J]. 气象, 34(6): 95-110. |
王叶红, 赵玉春, 崔春光, 2004. 雷达降水资料一维变分同化的敏感性研究[J]. 气象, 30(4): 6-10. DOI:10.7519/j.issn.1000-0526.2004.04.002 |
Evensen G, 1994. Sequential data assimilation with a nonlinear quasi-geostrophic model using Montre Carlo methods to forecast error statistics[J]. J Geo Res, 99(C5): 10143-10162. DOI:10.1029/94JC00572 |
Snyder C, Zhang Fuqing, 2003. Assimilation of simulated doppler radar observations with an ensemble Kalman filter[J]. Mon Wea Rev, 131: 1663-1677. DOI:10.1175//2555.1 |
Sun J, Crook N A, 1997. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint: Part Ⅰ. Model development and simulated data experiments[J]. J Atmos Sci, 54: 1642-1661. DOI:10.1175/1520-0469(1997)054<1642:DAMRFD>2.0.CO;2 |
Dowell D, Zhang F, Wicker L J, et al, 2004. Wind and temperature retrievals in the 17 May 1981 Arcadia, Oklahoma supercell: Ensemble Kalman filter experiments[J]. Mon Wea Rev, 132(8): 1982-2005. DOI:10.1175/1520-0493(2004)132<1982:WATRIT>2.0.CO;2 |
许小永, 刘黎平, 郑国光, 2006. 集合卡尔曼滤波同化多普勒雷达资料的数值试验[J]. 气象学报, 30(4): 712-728. |
Tong Mingjing, Xue Ming, 2005. Ensemble Kalman filter assimilation of Doppler radar data with a compressible nonhydrostatic model: OSS Experiments[J]. Mon Wea Rev, 133(7): 1789-1807. DOI:10.1175/MWR2898.1 |
Xue Ming, Tong Mingjing, 2006. An OSSE framework based on the ensemble square root Kalman filter for evaluating the impact of data from radar networks on thunderstorm analysis and forecasting[J]. J Atmos Oce Tech, 23(1): 46-66. DOI:10.1175/JTECH1835.1 |
Zhang Fuqing, Weng Yonghui, 2009. Cloud-resolving hurricane initialization and prediction through assimilation of doppler radar observations with an ensemble Kalman filter[J]. Mon Wea Rev, 137(7): 2105-2125. DOI:10.1175/2009MWR2645.1 |
Smith P L, Myers Jr C G, Orville H D, 1975. Radar reflectivity factor calculations in numerical cloud models using bulk parameterization of precipitation processes[J]. J Appl Meteor, 14: 1156-1165. DOI:10.1175/1520-0450(1975)014<1156:RRFCIN>2.0.CO;2 |
Lin Y-L, Farley R D, Orville H D, Bulk parameterization of the snow field in a cloud model[J]. J Climate Appl Meteor, 22: 1065-1092. DOI:10.1175/1520-0450(1983)022<1065:BPOTSF>2.0.CO;2 |
Houtekamer P L, Mitchell H L, 2001. A sequential ensemble Kalman filter for atmospheric data assimilation[J]. Mon Wea Rev, 129: 123-137. DOI:10.1175/1520-0493(2001)129<0123:ASEKFF>2.0.CO;2 |
Gaspari G, and Cohn S E, 1999. Construction of correlation functions in two and three dimensions[J]. Quart J Roy Meteor Soc, 125: 723-757. DOI:10.1002/(ISSN)1477-870X |
Murphy J M, 1988. The impact of ensemble forecasts on predictability[J]. Quart J Roy Meteor Soc, 114: 463-493. DOI:10.1002/(ISSN)1477-870X |
 2012, Vol. 38
2012, Vol. 38 