引言

洋口港位于江苏省南通市如东县东部沿海，是中国沿海中部唯一能建30万吨级的天然深水良港，它的开发建设作为江苏沿海开发的核心工程，已经列入国家战略布局，对整个中国沿海开发和能源安全具有重要战略意义。该港口地处江淮下游，是暖温带与亚热带过渡地带，冷暖气流频繁交汇，气候复杂多变，雷暴活动和雷电灾害频繁，加强对该地区雷暴天气的分析与研究，提高对洋口港地区雷暴活动的预报能力，具有重大意义。

雷暴云的发展与热气团在不稳定环境中的对流抬升有关^[1-2]，所以雷暴事件与大气的不稳定因子之间必然有一定关系。陈艳等^[3]采用中尺度数值模式模拟一次暴雨过程后指出，对流有效位能、风暴相对螺旋度等参数对强对流过程的发生发展有较好的指示作用。赵秀英等^[4]和高守亭等^[5]也分别把与动力、热力都相关的风暴强度指数、里查森指数用于强对流发生机制的研究。张翠华等^[6]研究发现, 中层(700~400 hPa)平均相对湿度与地闪活动有较好的相关性。郑栋等^[7]使用对流性稳定度指数、抬升指数、对流有效位能和700 hPa相当位温等指数综合预报闪电活动。陈秋萍等^[8]、郝莹等^[9]分别采用逐步消空法和指标叠加法进行基于对流参数的雷电预报。Solomon等^[10]在研究新墨西哥州雷暴时，使用了对流有效位能和抬升指数等因子，并发现当对流有效位能的值>400 J·kg^-1时，可以较好地预报闪电活动的发生，而抬升指数不是预报闪电活动的关键因子。

上述研究中，对单个或少数对流参数的研究较多，对各种对流参数与雷暴的相关性进行全面考察的少；且以有限的个例为研究样本较多，建立基于长时间序列样本，预报效果较稳定的雷暴预报方程的少。此外，从上述研究可以看出，由于地域的差异及预报方法的不同，雷暴事件与一些参数的相关性也存在一定差异。本文分析了江苏省洋口港地区2001—2009年4—9月1645个样本22种对流参数与雷暴事件的相关性及统计特征，优选因子，采用二级逻辑回归的方法，逐月建立雷暴预报方程，形成较为完善、稳定的基于对流参数的雷暴预报方法。

1 本文所使用资料

本文根据江苏省气象台普查后取得的NCEP再分析资料，经整理后借助MICAPS 3.0的T-lnp软件模块，计算2001—2009年4—9月1645个样本中(其中雷暴日242天，非雷暴日1403天)江苏地区154个格点不同时刻的22种对流参数，并选取处于洋口港地区的所有格点的各参数的算术平均值作为该区域相应参数的历史资料。

本文所使用的雷暴日资料来源于江苏省气候中心，因洋口港开发建设不久，没有专门的雷暴观测资料，所以使用其相邻市县观测站2001—2009年4—9月的雷暴日资料，规定若其相邻市县同时有2个或以上发生雷暴活动，则记为该区域的雷暴日。

2 预报因子的选取 2.1 各因子的相关系数

将该区域当日是否是雷暴日情况设为Y，有雷暴时，Y=1，无雷暴时，Y=0，则Y为“0”、“1”变量。X_i是各参数值，为连续型变量。使用下式求出X_i与Y的点双序列相关系数^[11]，可以考察各个参数X和Y之间的相互关系(线性相关)。

$r = \frac{{\bar X\left( 1 \right) - \bar X}}{{{S_X}}}{\left( {\frac{P}{{1 - P}}} \right)^{\frac{1}{2}}}$

(1)

式中，X为因子X_i的平均值，X(1) 为Y=1时，X_i的平均值，P为Y=1事件出现的频率，S_X为因子的样本标准差。

使用式(1) 求得1645个样本(其中雷暴日242天，非雷暴日1403天)中各因子各自与当日是否为雷暴日情况Y的点双序列相关系数，相关系数大于0.3的参数如表 1，并且均通过双尾检验^[11] Sig.(2-tailed)＜0.05。

由表 1可以看到，沙氏指数、条件对流稳定度指数、全总指数、抬升指数、对流稳定度指数、对流有效位能、风暴强度指数、杰弗逊指数、K指数、抬升凝结高度温度、上下层温差、大气可降水量、修正K指数、莱克利指数、风暴相当螺旋度与是否发生雷暴情况Y的点双序列相关系数在0.3以上，沙氏指数最高，达到0.544。其中，沙氏指数、抬升指数、对流稳定度指数、条件对流稳定度指数这几个因子均是通过计算气块在不同高度处的温度差来反映大气的不稳定情况，公式和物理意义相似，根据预报因子不可重复的原则，故只选取其中相关系数最大的沙氏指数；同理，K指数、修正K指数只选取K指数，杰弗逊指数、莱克利指数只选取杰弗逊指数；对流有效位能与风暴强度指数只选取风暴强度指数。

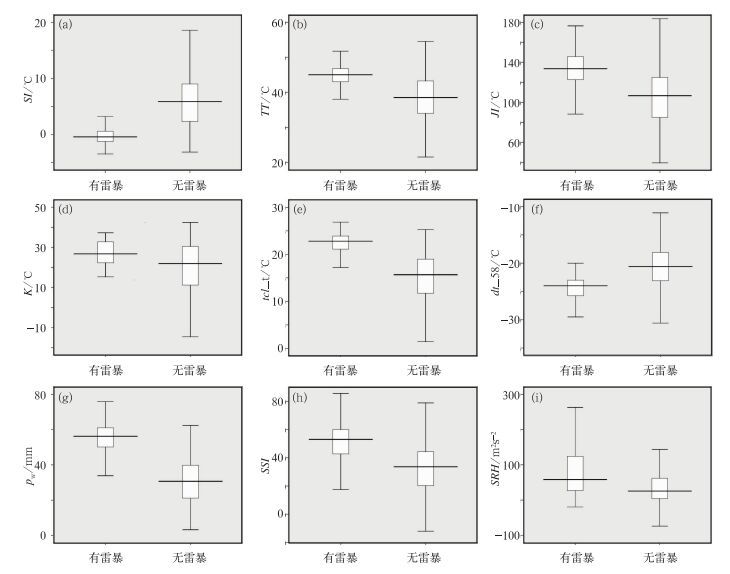
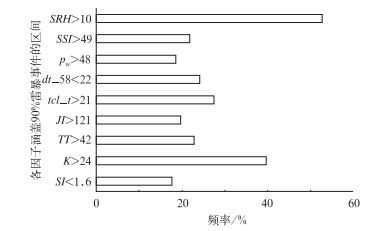
2.2 各因子在有无雷暴情况下的统计特征

统计学中，箱线图(Boxplot，又称箱图)可以直观地反映较大容量样本的值分布情况，并且排除异常数据点^[12]。图 1是2001—2009年1645个样本中有无雷暴情况下各对流参数的箱图。理想情况下，当某预报因子在有无雷暴情况下取值完全不同，即值域不相交时，则该因子对雷暴预报具有完全的指示作用，此时有无雷暴情况下的箱图在y轴应没有任何交集，即任意一个y值至多只经过一个箱图。从图 1看到，各参数有无雷暴时的箱图均存在一定的交集，有些相交较少，如图 1a的沙氏指数；有些则相交较多，如图 1d的K指数和图 1i的风暴相当螺旋度。显然，交集越少，则该参数对雷暴的指示作用越好。设各因子涵盖90%雷暴事件的取值区间为θ_i，非雷暴情况下，各因子取值落在θ_i区间内的频率η如图 2所示。可以看到，SI、TT、JI、tcl_t、dt_58、p_w、SSI的η均未超过30%，有无雷暴情况下的取值交加较少(如图 1a、b、c、e、f、g、h)，对于是否发生雷暴事件具有良好的指示作用。而K指数和风暴相当螺旋度的η分别为38.7%和52.8%，值域在有无雷暴情况下存在较多的交集(如图 1d、i)。因此，若引入K指数或风暴相当螺旋度作为预报因子，必然会带来较多的空报。

所以，本文使用沙氏指数SI、全总指数TT、杰弗逊指数JI、抬升凝结高度温度tcl_t、上下层温差dt_58、大气可降水量p_w、风暴强度指数SSI这7个参数作为预报因子。

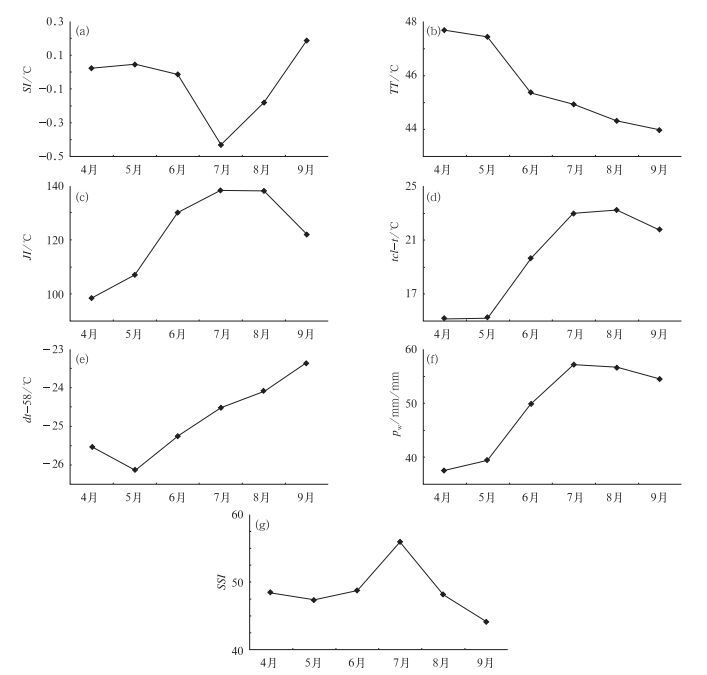
3 预报方程的建立 3.1 各参数的月分布特征

统计了2001—2009年4—9月洋口港地区的242次雷暴事件，得到各参数雷暴日的月均值分布如图 3。沙氏指数、杰弗逊指数、抬升凝结高度温度、大气可降水量、风暴强度指数的雷暴日均值均是在7、8月份达到正的或负的最大值，4、5月份相对较小，这是因为7、8月份对流活动最为旺盛，气层不稳定程度高；全总指数、上下层温差则是在4、5月份达到正的或负的最大值，这可能是由于这两个参数公式中的T₅₀₀春季容易出现较强低温。可见各参数都存在明显的月变化特征，因此，本文对4—9月逐月建立预报方程。

3.2 使用二级逻辑回归法建立各月预报方程 3.2.1 建立预报方程

逻辑回归的基本思想是把预报量和因子均看成随机事件，随机事件出现与否用“0”和“1”表示，把预报量事件y与n个预报因子x₁, x₂, …, x_n事件之间的关系看成是n个因子已经出现的条件下事件出现与否的关系，则可以建立对预报量y的条件期望。逻辑回归中X为各因子“0”、“1”化之后的矩阵。Y作为预报量，也要进行“0”、“1”化，当该样本为该区域的雷暴日时，则设y=1；否则，设y=0。

考虑各因子物理意义的相对独立性，并经过上述7个参数的组合试验以达到最佳拟合效果，第一级排空回归，我们选用含水量指标p_w、稳定度指标沙氏指数SI、热力指标全总指数TT和综合性指标杰弗逊指数JI作为因子。各因子的“0”、“1”化方法是：以各因子雷暴事件中的四分位数作为临界值，即将9年中各月各因子雷暴日的取值由小到大排列，并分成四等份，处于第一个分割点位置的是第一四分位数Q₁，处于第三个分割点位置的是第三四分位数Q₃^[11]。从上一章中图 1可以看到，p_w、TT和JI雷暴日的取值较非雷暴日大，则X_i＜Q₁时，设为“1”，否则设为“0”；SI雷暴日的取值较非雷暴日小，则X_i＞Q₃时，设为“1”，否则设为“0”。经过拟合计算，得到排空回归方程(为便于阅读，式中因子用()括起，下同)：

$y = {b_0} + {b_1}\left( {JI} \right) + {b_2}\left( {SI} \right) + {b_3}\left( {TT} \right)$

(2)

回归结果得到，雷暴情况下，即当y=1时，使用上式求得的预测y′≤k₁，则将样本中经式(2) 计算后得到的预测y′＞k₁的排除，剩余样本进入第二级预报回归。

第二级预报回归使用风暴强度指数SSI，抬升凝结高度温度tcl_t，上下层温差dt_58作为参数。各因子的“0”、“1”化也是以各因子雷暴事件中的四分位数作为临界值。对于SSI和tcl_t，当X_i≥Q₁时，设为“1”，否则设为“0”；对于SI，当X_i≤Q₃时，设为“1”，否则设为“0”。经过拟合计算，得到预报方程：

$y = {c_0} + {c_1}\left( {SSI} \right) + {c_2}\left( {tcl\_t} \right) + {c_3}\left( {dt\_58} \right)$

(3)

回归结果得到，雷暴情况下，即当y=1时，使用上式求得的预测y′≥k₂，则当样本中经式(3) 计算后得到的预测y′＞k₂时，作为预报有雷电发生的阈值。

使用上述方法，逐月求得排空方程和预报方程如表 2。

对各月的二级回归方程均进行了F检验^[12]，并且求得“0”、“1”化之后的回归因子与预报量的复相关系数如表 2。Sig.F∈[4.99×10^-6, 0.0065]，所以认为我们建立的回归模型是可以接受的^[11]；复相关系数R∈[0.49, 0.8]，雷暴事件集中的6—8月R值均在0.6以上，说明我们选取的因子和设立的门限对于预报量具有良好的指示作用。

3.2.2 拟合结果分析

使用上述方法，对2001—2009年4—9月的1645个样本进行拟合结果分析，其中^[13]，

$命中率POD = \frac{{{n_1}}}{N}$

(4)

$虚警率FAR = \frac{{n\prime }}{n}$

(5)

$临界成功指数CSI = \frac{{{n_1}}}{{N + n\prime }}$

(6)

式中，N为实况雷暴事件次数，n₁为报出的雷暴事件次数，n′为预报有雷暴实况无雷暴事件次数，n为预报有雷暴次数。

如表 3可见，命中率的平均值为84.9%，最高为7月的91.5%，最低为5月的80.0%；虚警率的平均值为26.1%，最低为7月的21.2%，最高为5月的33.3%；临界成功指数的平均值为62.8%，最高为7月的70.3%，最低为5月的55.7%。因此可以认为我们建立的预报模型拟合程度较好。

3.2.3 对2010年4—9月184个样本进行试报

使用上述方法，对2010年4—9月的样本进行试报，样本容量184个，其中，雷暴日31天，非雷暴日153天。试报结果为：报警41次，命中27次，空报16次，命中率87.1%，虚警率39%，临界成功指数57.4%。

各月的预报结果如表 4，可以看到，各月雷暴事件命中率均在80.0%以上，7—9月份的临界成功指数较高。由于2010年5月没有发生雷暴，4和6月雷暴事件分别只有1和2次，样本较少，试报结果难免具有一定偶然性，需要更多样本进行验证。

4 小结和探讨

本文基于洋口港地区2001—2009年4—9月1645个样本，探讨了对流性天气指数对于雷电预报的指示作用，得到以下结论：

(1) 本文计算分析22种对流参数与雷暴事件的相关性得出：沙氏指数、全总指数、杰弗逊指数、抬升凝结高度温度、上下层温差、大气可降水量、风暴强度指数等参数的点双序列相关系数较高，在0.3以上；且在不同天气条件下(是否发生雷暴)的区分度较好，在涵盖90%雷暴事件的参数区间内，非雷暴事件发生的概率都没有超过30%，对于雷暴具有良好的甄别指示作用。

(2) 本文统计了2001—2009年4—9月洋口港地区的242次雷暴中各参数的逐月均值，分析得到：沙氏指数、杰弗逊指数、抬升凝结高度温度、大气可降水量、风暴强度指数的雷暴日均值均是在7、8月达到正的或负的最大值，4—9月相对较小；全总指数、上下层温差在4、5月达到正的或负的最大值。各参数均存在明显的月变化特征。

(3) 本文选择与雷暴事件具有较好相关性的参数作为因子，并考虑到各参数月际数值分布差异，使用不同月份的p_w，SI，TT，JI的不同阈值作为排空因子，不同月份的SSI，tcl_t，dt_58的不同阈值作为预报因子，使用二级逻辑回归法建立排空方程和预报方程。经检验，复相关系数R>0.48，Sig.F＜0.02；经拟合结果分析，命中率平均值为84.9%，虚警率平均值为26.1%，临界成功指数的平均值为62.8%；使用2010年4—9月184个样本(31个雷暴事件)进行试报，临界成功指数为57.4%，达到一定预报效果。

由于本文所使用的样本中4、5和9月的雷暴事件较少，预报结果难免存在一定的偶然性，还需要更多的资料进行验证。另外，我们的预报方法没有考虑与环流形势的结合和触发因子，接下来的工作中，我们将开展这方面的研究，进一步改进和完善我们的预报方法。