2. 中国气象局数值预报中心,北京 100081;
3. 山东省气象科学研究所,济南 250031
2. Numerical Weather Prediction Centre, CMA, Beijing 100081;
3. Shandong Provincial Meteorological Institute, Jinan 250031
极端天气事件是一种在特定地区和时间内罕见的天气事件,具有破坏性大、突发性强和难以预测等特点。政府间气候变化专门委员会(Intergovernmental Panel on Climate Change,IPCC)第三次评估报告[1]与第四次评估报告[2]对极端天气事件给出明确定义:极端天气事件是指其发生概率小于观测记录概率密度函数第10个百分位数或超过第90个百分位数的天气事件。我国气候与自然地理条件复杂,受亚洲季风系统的影响,各种极端气象灾害及其衍生灾害频繁发生,具有种类多、强度大、频率高、危害严重等特点,其中主要包括洪涝、干旱、高温热浪、低温冷害等灾害性极端天气事件,给国民经济发展和人民生命财产造成严重损失。向社会和公众提供极端天气事件准确的预测预报,对国家防灾减灾是非常必要的。
近些年对极端天气事件的研究受到气象界高度的重视。前期的研究主要是利用统计方法分析极端天气事件变化特征和趋势。任福民等[3]对我国极端温度的区域分布以及季节变化特征进行了分析研究,认为近40年中国季极端最低温度以春、秋两季为最大, 大变率区域主要集中在北方。翟盘茂等[4]研究了中国过去45年中降水强度等方面的极值变化趋势,结果显示:平均降水强度极端偏高的区域范围呈现扩大趋势。
在过去的十多年中, 数值天气预报取得了迅速的发展, 利用数值预报模式模拟分析暴雨、台风等极端天气成为可能[5]。目前越来越多的气象学者开始使用数值天气模式对极端天气事件的形成机理进行模拟。程相坤等[6]利用中尺度数值模式(Mesoscale Model 5 Version 3.7,简称MM5V3.7) 对2007年3月3—5日大连地区出现的暴雨、雨凇与寒潮等多种灾害性极端天气进行了分析,认为这次极端天气是由北上江淮气旋与北方冷空气共同作用造成的。苗春生等[7]利用天气预报模式(Weather Research and Forecast model,WRF)对2008年1月25—29日中国低温雨雪冰冻天气过程进行模拟,结果发现:长江中下游及以南地区长时间存在着高低空急流的耦合形态和由低空急流不断输送来的暖湿水汽,使这些区域低层的水汽辐合, 促进大范围雨雪天气维持。
由于大气是一个混沌系统,小概率极端天气事件的发展演变存在诸多不确定性,用单一数值天气模式预报其未来演变是不严谨的,对极端天气事件的预报预测仍然存在巨大的挑战。自20世纪90年代国际上引入集合预报以来,不少研究成果表明,集合预报可以弥补单一数值预报模式的预报不确定性[8-10]。Lalaurette[11]基于欧洲中期天气预报中心(European Centre for Medium-range Forecast,ECMWF)集合预报系统,研究了一种可识别极端天气事件的极端天气预报指数,其基本思路是通过定义一个数学函数来计算某一预报要素累积概率分布函数的气候值与集合预报系统集合成员产生的预报值之间的连续差异,通过确定某一阈值识别未来是否发生极端降水、极端低温和极端大风等极端天气事件。ECMWF将此函数值定义为极端天气预报指数(Extreme Forecast Index, EFI)。Lalaurette利用EFI对1999年圣诞节期间发生在法国、德国、英格兰和意大利的“圣诞风暴”进行预报试验,结果显示EFI可提前120小时识别出极端大风发生区域。2001年ECMWF将EFI投入到业务应用,产品主要包括预报时效为1~5天的2 m温度、10 m风速和24 h累积降水量的EFI等,这些产品极大地提高了极端天气预报能力。近年来ECMWF的气象学者继续对EFI进行改进,Lalaurette[12]基于Anderson-Darling检验修正了原始的EFI公式,Zsoter[13]使用修正过的EFI公式对2005年10月西欧持续极端高温进行研究,结果发现:与原始的EFI相比,修正公式后的EFI能识别出更多发生极端高温的区域。Zsoter[13]使用ECMWF的再分析资料(40-year re-analysis,ERA-40) 中的1971—2000年30年的数据代替原有3年T159集合预报模式数据生成新的模式气候累积概率分布,结果显示:在新的模式气候累积概率分布中,要素极小值趋于更小,极大值趋于更大,基于新模式气候累积概率分布计算得到的EFI能更准确地识别出极端天气发生的区域。
我国已经建立了基于T213谱模式的全球集合预报系统,2011年6月1日,国家气象中心集合预报产品首次下发全国气象台站,我国集合预报产品的应用进入新阶段。集合预报的一大优势是可以根据一组预报结果给出未来大气状态的概率分布,以此对小概率的极端天气事件做出预报。但是目前集合预报产品比较单一,主要是传统的集合预报产品,如集合平均图、要素预报概率图等,无法给出极端天气的直观预报信息,集合预报对极端天气事件的预报优势得不到充分发挥[14-16]。如何利用我国T213集合预报产品对极端天气做出更好的预报,非常值得研究。本文借鉴Lalaurette的EFI数学处理方案,充分结合我国T213集合预报数据的现状和特点,研究基于T213集合预报模式的EFI数学处理方法,并利用EFI对我国2008年1月低温天气进行预报试验和评估检验,以期提高极端低温事件预警能力。
1 EFI的简介及预报原理 1.1 EFI的定义及性质根据Lalaurette[11]定义,EFI是测量某一预报要素累积概率分布函数的气候值与集合预报成员产生的预报值之间连续差异的预报指数。统计学中常采用柯尔莫可洛夫-斯米洛夫检验方法(Kolmogorov-Smirnov test,K-S检验)测量两组累积概率分布的差异是否具有统计显著性[17],K-S检验公式如下:
| $K = \mathop {{\text{max}}}\limits_{ - \infty < x < + \infty } |{F_1}\left( x \right) - {F_2}\left( x \right)|$ | (1) |
其中F1(x)与F2(x)代表预报要素的两组累积概率分布函数,K值代表它们在空间分布上绝对偏差的最大值。若K值超过一定置信区间,说明两组累积概率分布函数差异具有统计显著性。
EFI不单要计算气候累积概率分布与集合预报累积概率分布在某一点处的差值,而且还要计算两者的连续差异。连续分级概率评分(Continuous Ranked Probability Score,CRPS)[18]是一种概率预报检验方法,可以计算两组数据累积概率分布的连续差异。CRPS计算公式如下:
| $CRPS = \smallint _{ - \infty }^{ + \infty }{\left[ {{F_1}\left( x \right) - {F_2}\left( x \right)} \right]^2}{\rm{d}}x$ | (2) |
由公式(2) 可以看出,CRPS总为非负值。我们希望EFI是一种带符号的指数,它不仅可以计算气候累积概率分布与集合预报累积概率分布的连续差异,而且其正负性可以指示这种差异的方向是否会带来极端天气灾害,比如极端小的风就不会影响人们的日常生活。Lalaurette [11]根据公式(1) 和(2),定义EFI数学计算公式为:
| $EF{I_{2m + 1}} = 2\left( {m + 1} \right)\smallint _0^1{\left[ {p - {F_f}\left( p \right)} \right]^{2m + 1}}{\rm{d}}p$ | (3) |
其中,p是气候累积概率分布函数,Ff(p)是集合预报累积概率分布函数。m是经验值,Lalaurette定义m为1,EFI可表示为EFI3。
从式(3) 可看到EFI3有以下几点性质:
(1)EFI3在-1和1之间取值,如果所有集合预报系统(ensemble prediction system, EPS)成员的预报结果小于气候累积概率分布的最小值,即对气候累积概率分布中所有的分位数,Ff(p)=1,这时EFI3为-1,代表预报要素出现极端低值的天气事件可能性越大,如极端低温事件;如果所有的EPS成员预报结果大于气候累积概率分布的最大值,即对气候累积概率分布中所有的分位数,Ff(p)=0,这时EFI3为1,代表预报要素出现极端高值的天气事件可能性越大,如极端高温事件等。EFI3越接近1(-1),表示极端天气事件发生的可能性越大。
(2) 如果所有EPS成员的预报结果相同,这个预报值在气候累积概率分布中对应的累积概率为p0,将其带入公式(3)
| $EF{I_{2m + 1}} = 2\left( {m + 1} \right)\smallint _0^1{\left( {p - {p_0}} \right)^{2m + 1}}{\rm{d}}p$ | (4) |
此时,EFI3公式如下:
| $EF{I_3} = {({p_0} - 1)^4} - {p_0}^4$ | (5) |
根据1.1中介绍的EFI3的性质可知,EFI3预报极端天气的原理是确定某一EFI3值作为发布极端天气预警信号的临界阈值。若EFI3绝对值大于这一阈值,则判断会发生极端天气,若EFI3的绝对值小于这一数值,则判断没有极端天气发生。目前,ECMWF将发布极端天气预警信号的EFI3值定为0.5[11]。
2 T213集合预报系统简介2002年9月1日国家气象中心建立了全球中期数值预报系统(T213L31, T213),这是从ECMWF引进后经我国数值预报人员移植开发的。T213模式采用地形追随等压面混合坐标,在垂直方向上有31层,模式顶到达10 hPa;水平分辨率为60 km。模式系统包含一整套比较先进的物理过程。2006年12月国家气象中心建立了基于T213模式的全球中期集合预报系统,该系统同化方案采用NCEP谱统计插值方案(Spectral Statistical Interpolation,SSI),初值扰动方法采用增长模繁殖法,集合预报成员数为15个,2007年7月T213集合预报模式数据开始存档。
3 基于我国T213集合预报的EFI3数学处理方案及应用试验2008年1月10日至2月2日, 我国发生了4次强烈的低温雨雪冰冻天气过程, 分别是2008年1月10—16日,1月18—22日,1月25—29日,1月31日至2月2日,其中以第三次低温过程强度最大,表现为平均气温明显偏低。这次我国大范围低温天气是一次典型的极端低温天气事件。下面以第三次低温天气过程(1月25—29日)为例,利用上文中介绍的EFI3对其进行极端低温预报试验。
3.1 气候累积概率分布计算方案从式(3) 可知,EFI3是基于气候与EPS各成员预报结果累积概率分布计算生成的。因此EFI3的计算涉及两部分,一是气候累积概率分布,二是集合预报累积概率分布。气候累积概率分布可采用观测资料产生(以下简称观测气候累积概率分布),也可采用模式历史资料产生(以下简称模式气候累积概率分布)。以武汉2 m温度气候累积概率分布方案为例,分析武汉站的观测气候累积概率分布和模式气候累积概率分布的差异,确定采用哪一种数据生成EFI3中的气候累积概率分布。
由于目前我国T213集合预报数据时间序列仅有4年,无法获得标准时段(30年)模式气候数据,参照Lalaurette[11]的方法,采用以下步骤产生T213模式气候累积概率分布。
(1) 选取T213集合预报模式2008年12月,2009年1月和2009年2月3个相邻月12 UTC发布的2 m温度逐日资料。
(2) 选取24、120和240 h时效的预报场数据,每个预报场有15个集合预报成员。
(3) 利用上面选取的数据计算涵盖中国区域内各个格点的模式气候累积概率分布。
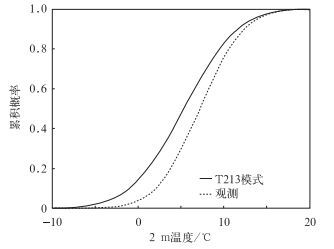
利用双线性插值将2 m温度累积概率分布结果插值到武汉站,生成武汉2 m温度模式气候累积概率分布,利用同期武汉2 m温度观测资料生成观测气候累积概率分布,如图 1所示。
|
图 1 武汉2 m温度累积概率分布 (实线:T213集合模式预报数据,虚线:观测数据) Fig. 1 Cumulative probability distribution of 2 m temperature in Wuhan (Solid line represents the data of ensemble forecast from T213 model, and dashed line the data of observation) |
由图 1可见,基于T213集合预报生成的模式气候累积概率分布位于观测累积概率分布的左侧,在0.1~0.8的累积概率区间,模式预报值普遍较观测值低1~2℃,即T213模式2 m温度的预报存在负的偏差。如使用观测数据生成气候累积概率分布,就会对EFI3的计算结果产生影响。为了使EFI3计算结果不受模式误差因素的影响,我们采用T213集合预报模式数据生成气候累积概率分布。
3.2 集合预报累积概率分布的计算方案接下来我们按照以下步骤生成EPS各成员预报结果的累积概率分布:
(1) 选取T213集合预报模式2008年1月20—24日,1月21—25日和1月22—26日三个时段12 UTC发布的2 m温度资料。
(2) 从上面三个时段预报资料中分别选取120、96和72 h时效的预报场数据,每个预报场有15个集合预报成员。
(3) 利用上面选取的数据计算涵盖中国区域各个格点的EPS各成员预报结果的累积概率分布。
3.3 基于T213集合预报EFI3的阈值确定EFI3阈值以风险评分(Threaten Score,TS)评估方法获得。在每个格点上,考虑极端低温事件发生或不发生两种状态。检验结果为预报正确、预报错误和漏报。用双态列联表来表示,见表 1。表 1中,h和c为预报正确,f为预报错误,m为漏报。TS公式如下:
|
|
表 1 双态分类列联表 Table 1 Contingency table of dimorphic distribution |
| $TS = h/\left( {h + m + f} \right)$ | (6) |
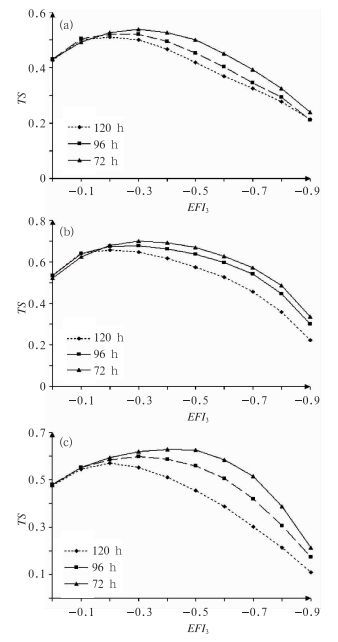
图 2给出了2008年1月3次低温过程120、96与72 h预报时效的EFI3平均TS评分。由图可见,在3次低温过程中,在[-0.2, 0]的区间上,三个时效EFI3的TS评分是相同的;在[-0.9, -0.3]的区间上,三个时效EFI3的TS评分随着预报时效的延长,TS值不断变小。
|
图 2 2008年1月3次低温过程不同预报时效的EFI3的平均TS评分(a) 1月10—16日,(b) 1月18—22日,(c) 1月25—29日 Fig. 2 The averaged TS scores of EFI3 valid for extreme low temperature, (a) from 10 to 16 January 2008, (b) from 18 to 22 January, and (c) from 25 to 29 January (The short dashed line represents 120 h, the long dashed line represents the 96 h, and the solid line represents the 72 h) |
表 2给出了4次低温过程各个时效EFI3值所对应的最大TS值。由表可见,EFI3值分布在[-0.4, -0.2]区间上。-0.2与-0.3均出现4次,-0.4出现1次,由于EFI3为-0.3时,对应TS值较大故本文将-0.3确定为EFI3发布极端低温预警信号的阈值。
|
|
表 2 三次低温过程各时效EFI3值对应最大TS评分值 Table 2 The EFI3 value corresponding to maximal TS value in every lead time |
以2008年1月27日为例(其他4天情况大致相同,不再累述),使用-0.3作为发布极端低温预警信号的阈值,分析EFI3对极端低温天气120、96与72 h三个时效的识别效果。
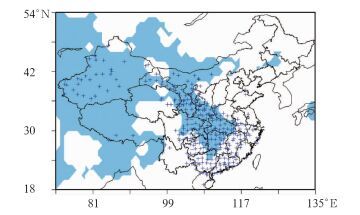
首先取T213集合预报模式中27日12 UTC 00 h发布的2 m温度控制预报作为分析场,如果分析场中格点的2 m温度值小于对应格点的模式气候累积概率分布第十个分位数,我们定义这个格点出现极端低温,然后利用全国756个观测站1971年至2000年1月逐日观测数据中平均温度值生成观测气候累积概率分布,若27日测站平均温度小于观测气候累积概率分布第十个分位数对应的平均温度值,定义此站出现极端低温。按照上述方式生成27日极端低温的分布图,如图 3所示。
|
图 3 2008年1月27日极端低温分布图 (阴影部分代表模式分析场生成的极端低温区域,叉号代表出现极端低温的测站) Fig. 3 The distribution of extreme low temperature on 27 January 2008 (The shaded area represents the area of extreme low temperature and the crosses represent the stations of extreme low temperature) |
从图 3中不难发现,除了在贵州西部、云南、广东、江西和长沙没有极端低温出现外,由分析场产生的极端低温分布范围和出现极端低温的测站分布范围大致相同。可见选取的模式气候累积概率分布能较真实地反映出实际2 m温度的气候特征。下面利用分析场产生的低温分布查看EFI3各个时效对极端低温天气的识别效果。
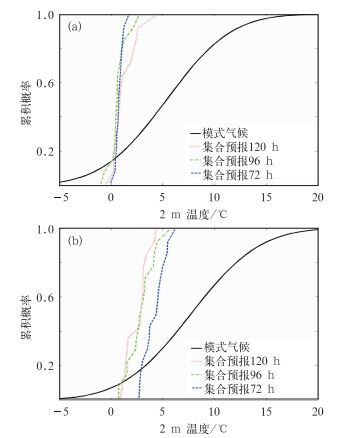
图 4给出武汉与长沙两个站的模式气候累积概率分布与EPS各成员120、96及72 h预报时效的集合预报累积概率分布。从图 4a可以看出,在-1~1℃的温度区间,武汉站的120、96和72 h预报时效EPS累积概率值分别为0.6、0.7和0.8,而对应其模式气候累积概率为0.1~0.2,根据公式(3),武汉120、96和72 h预报时效的EFI3计算结果分别为-0.274、-0.372和-0.405,随预报时效增加而增大,由发布低温预警的阈值为-0.3可知,EFI3会提前96 h识别出武汉出现极端低温;从图 4b可见,长沙120、96和72 h的EPS温度预报均大于0℃,在1~3℃温度区间,120、96和72 h预报时效的EPS累积概率分别为0.8、0.65和0.23,而模式气候累积概率为0.1至0.2,EFI3计算结果分别为-0.392、-0.323和-0.203,随预报时效增加而减少,表明可提前72 h识别出长沙不会出现极端低温。
|
图 4 1月27日模式格点气候累积概率分布及该日相应72、96和120 h集合预报结果累积概率分布比较(a)武汉(31°N、114°E),(b)长沙(28°N、113°E) (黑色实线代表模式气候,红色虚线代表EPS成员120 h预报,绿色点化线代表EPS成员96 h预报,蓝色双划线代表EPS成员72 h预报;以1月27日模式分析场产生的极端低温分布进行预报) Fig. 4 Cumulative probability distributions of model climate and EPS at (a) Wuhan (31°N, 114°E) and (b) Changsha (28°N, 113°E) (Black solid line represents the model climate, red dash line represents the EPS 120 h forecast, green dotted line represents the EPS 96 h forecast, and blue double dashed represents the EPS 72 h forecast (valid on 27 January 2008) |
图 5给出了识别27日极端低温120、96和72 h EFI3分布图。对比图 4极端低温分布看,若将发布极端低温的EFI3的阈值定为-0.3,在120 h的EFI3分布图上(图 5a),湖南北部、湖北和重庆大部分地区,四川东部、新疆和甘肃大部分地区会出现极端低温预警信号;在96 h的EFI3分布图上(图 5b),除了上述区域外,西藏、甘肃、陕西,河南大部分地区出现极端低温预警信号;在72 h的EFI3分布图上(图 5c),出现低温预警信号的区域基本与分析场产生的极端低温的区域相似。
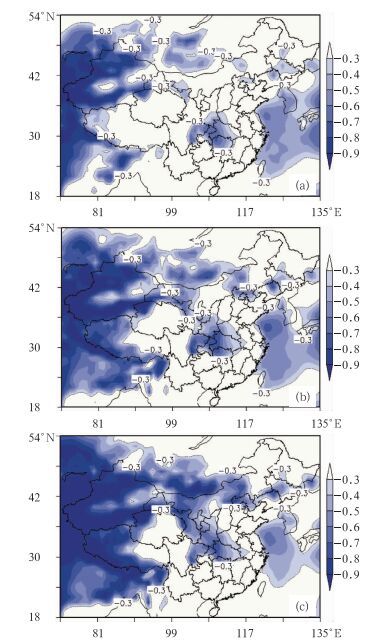
|
图 5 2 m温度各时效120 h (a),96 h (b)和72 h (c)EFI3分布图 Fig. 5 EFI3 maps of 2 m temperature valid on 27 January 2008 at 12 UTC(a)120 h, (b) 96 h, and (c)72 h |
需要注意的是,图 3中出现极端低温的区域与图 5中EFI3发出极端低温预警信号的区域并不完全一致。在上面三个时效的EFI3分布图中,湖南南部、贵州东北部与广西北部没有出现低温预警信号,在图 3由分析场产生的极端低温分布中,这些区域出现极端低温;渤海,东海等区域EFI3分布图出现极端低温预警信号,在图 3中这些地区并没有极端低温分布。造成上述的原因可能是现有EFI3表达式对EPS预报结果中的极端值并不是很敏感,如果EPS仅有少数成员报出极端低温,EFI3计算结果可能不会超出临界阈值;或者集合预报系统很多成员预报出异常低温,EFI3计算结果可能会超出临界阈值。但是总体来说,对于图 3中由分析场产生的大部分极端低温的区域,EFI3可以提前3~5天发出极端低温预警信号。
3.5 EFI3对极端低温天气识别技巧的评估检验相对作用特征(Relative Operating Characteristic,ROC)曲线常用来表征概率天气和气候预报技巧的方法[19]。下面利用ROC方法检验EFI3对极端低温天气的识别技巧。
图 6给出了2008年1月25—29日EFI3平均ROC曲线。图中每个点代表不同的EFI3值,从曲线左下方到右上方绝对值依次减小(-0.9,-0.8,…,0.0)。左下方的EFI3绝对值较大,表示发布极端低温预警信号的EFI3值较高,因此可以被识别到的极端低温事件较少,对应T213集合预报对极端低温预报的命中率小,错误警报率也较小;右上方的EFI3绝对值较小,表示发布极端低温预警信号的EFI3值较低,可以被识别到的极端低温事件较多,对应T213集合预报对极端低温预报的命中率大,其错误警报率也随着增大。图中三个时效的ROC曲线均在对角线以上,其面积值分别为0.680、0.657和0.542,说明基于T213集合预报生成的各时效EFI3对极端低温均存在正的识别技巧,随着预报时效的延长,识别技巧逐渐降低,这与模式预报精度随预报时效延长而下降的变化特征是一致的。
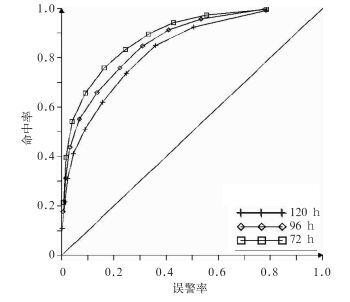
|
图 6 2008年1月25—29日2 m温度EFI3平均ROC曲线 Fig. 6 Relative Operating Characteristic curve valid for 2 m temperature EFI3 on 27 Januay 2008 at 12 UTC. Each point of the curve corresponds to a different EFI3 threshold. (Vertical axis represents the hit rate of EFI3, horizontal axis represents the false rate of EFI3) |
从式(3) 可以看到,EFI3值受模式气候累积概率分布影响较大,为了分析不同的模式气候累积概率分布对EFI3识别极端低温天气技巧的影响,下面使用另一种方法生成模式气候累积概率分布,评估使用不同的模式气候累积概率分布计算得到的EFI3对极端低温天气的识别技巧。
(1) 选取2003—2010年(2008年除外)1月T213模式12 UTC起报的逐日预报资料。
(2) 选取24 h时效的预报场数据,2003—2007年是国家气象中心存档的T213确定性模式预报资料,2009—2010年选取集合预报系统中未经扰动的控制预报资料。
(3) 利用上面选取的数据计算涵盖中国区域内各个格点的模式气候累积概率分布。
利用上述方法产生的模式气候累积概率分布,计算2008年1月27日的120、96与72 h的EFI3。
图 7a给出了由第二种模式气候累积概率分布产生的极端低温分布,与图 3相比,两套模式气候累积概率分布计算方案获得的极端低温分布范围大致相同。图 7b、7c和7d分别是利用第二种模式气候累积概率分布获得的27日极端低温的120、96和72 h EFI3分布图。与图 5相比,在图 7各时效EFI3分布图中,发出极端低温预警信号的范围明显缩小了,表明不同的模式气候累积概率分布对EFI3的计算结果有较明显影响。
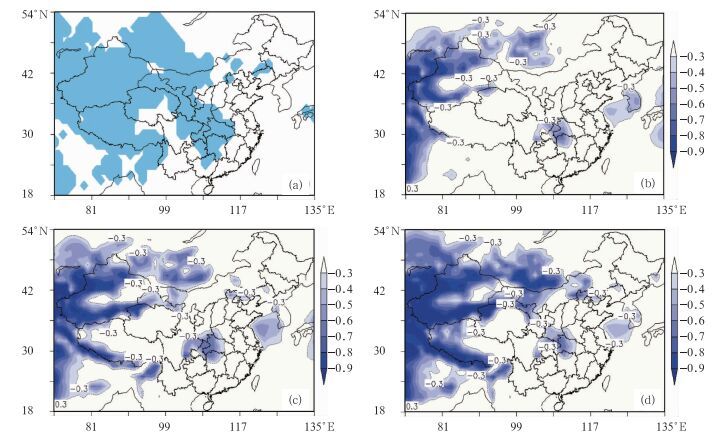
|
图 7 (a)同图 3,(b),(c)和(d)同图 5,但是为第二套模式气候累积概率分布所计算 Fig. 7 (a) same as Fig. 3, and (b), (c), (d) same as Fig. 5, but computed by using the second model climate cumulative probability distribution |
图 8给出了由两种模式气候累积概率分布计算得到的EFI32008年25—29日平均ROC曲线对比图。从图 8可见,各个预报时效两条ROC曲线均位于对角线之上,说明由两种模式气候累积概率分布生成的EFI3对极端低温天气均存在正的识别技巧。对比各时效两条ROC曲线相同的EFI3值所对应的确报率与错误警报率发现,第一套模式气候累积概率分布生成EFI3均高于第二套。总体来看,由第一套模式气候累积概率分布计算得到的EFI3对极端低温天气的识别技巧略高于第二套。
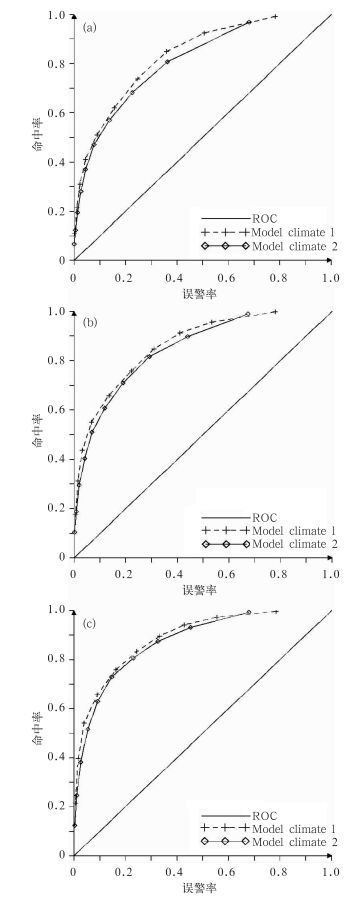
|
图 8 两套模式气候生成EFI3的2008年1月25—29日各时效平均ROC曲线对比图 (a) 120 h,(b) 96 h,(c) 72 h Fig. 8 The averaged ROC curves of EFI3 derived from two kinds of cumulative probability distributions of model climate valid for 2 m temperature during 25—29 January 2008 at 12 UTC (a) 120 h, (b) 96 h, and (c) 72 h |
出现上面原因可能是第一套模式气候所选取模式数据的初始场是2006年T213模式同化系统升级后为谱统计插值方案(SSI)同化系统生成的,而第二种模式气候所选取的模式数据初始场,即有2006年以前的最优插值方案(OI)同化系统产生的,又有2006年以后的SSI同化系统产生的,预报场误差特征不一致,不能很好地代表模式气候特征。由此可见,产生模式气候累积概率分布的数据序列并不是越长越好,模式数据预报误差的一致性是更加关键的因素。
5 结论本文基于我国T213集合预报模式资料,借鉴ECMWF的EFI数学处理方案,在分析T213模式数据特征基础上,研究我国T213集合预报系统的EFI的数学处理方法,建立了适合T213集合预报模式的EFI,并利用EFI3对2008年1月极端低温天气进行预报试验和评估检验,分析不同的模式气候累积概率分布对EFI3识别极端低温天气技巧的影响,得到以下结论:
(1) 通过对比2 m温度模式气候累积概率分布与观测气候累积概率分布差异,分析T213模式数据的特征,确定利用T213模式数据生成模式气候累积概率分布;在T213模式数据较短的情况下,利用所有集合预报成员预报结果生成模式气候概率分布。
(2) 利用TS评分确定EFI3发布极端低温预警信号的阈值为-0.3并进行预报试验。试验结果表明,EFI3对极端低温天气具有较好的识别能力。对于模式分析场产生极端低温的大部分区域,EFI3预报图中可提前3~5天发出预警信号。利用ROC曲线对EFI3识别极端低温的技巧进行评估检验。检验结果显示,基于T213集合预报生成的EFI3对极端低温存在正的识别技巧,随着预报时效的延长,识别技巧逐渐降低。
(3) 评估不同模式气候累积概率分布对EFI3识别极端低温天气技巧的影响。结果表明生成模式气候累积概率分布的数据序列并不是越长越好,模式数据预报误差的一致性是更加关键的因素。
本文研究表明,对于由模式分析场产生极端低温的区域,我们基本可从EFI3分布图上获得信息,EFI3对极端低温天气具有较好的识别能力。EFI3对其他气象要素(风、降水)的识别效果,还需要在今后的工作中进行单独研究。由于目前只能获取4年的T213集合预报模式数据,如何生成合理的模式气候累积概率分布还有待更多研究。随着T213集合预报模式数据的不断积累,将有助于产生更客观的模式气候累积概率分布,提高EFI3对极端天气的识别技巧。
Houghton J T, Ding Y, Griggs D J, et al. Climate Change 2001:The science of climate change[R]. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change[R]. Cambridge, United Kingdom an New York NY, USA: Cambridge University Press, 2001.
|
Solomon S, Qin D, Manning M, et al. Climate change 2007 : The physical science basis[R]. Contribution of Working Group I to the Fourth Assessment Report of the intergovernmental Panel on Climate Change. Cambridge, United Kingdom and New York, USA: Cambridge University Press, 2007.
|
任福民, 翟盘茂, 1998. 1951—1990年中国极端气温变化分析[J]. 大气科学, 22(2): 217-227. |
翟盘茂, 任福民, 1999. 中国降水极端值变化趋势检测[J]. 气象学报, 57(2): 208-216. DOI:10.11676/qxxb1999.019 |
矫梅燕, 2010. 天气业务的现代化发展[J]. 气象, 36(7): 1-4. DOI:10.7519/j.issn.1000-0526.2010.07.002 |
程相坤, 李燕, 邹耀仁, 2010. 大连地区一次极端天气的数值研究[J]. 中国海洋大学学报, 40(2): 001-008. |
苗春生, 赵瑜, 王坚红, 2010. 080125南方低温雨雪冰冻天气持续降水的数值模拟[J]. 大气科学学报, 33(1): 25-33. |
杜钧, 陈静, 2010. 单一值预报向概率预报转变的基础:谈谈集合预报及其带来的变革[J]. 气象, 36(11): 1-11. DOI:10.7519/j.issn.1000-0526.2010.11.001 |
陈法敬, 矫梅燕, 陈静, 2011. 一种温度集合预报产品释用方法的初步研究[J]. 气象, 37(1): 14-20. DOI:10.7519/j.issn.1000-0526.2011.01.002 |
任志杰, 陈静, 田华, 2011. T213全球集合预报系统物理过程随机扰动方法研究[J]. 气象, 37(9): 1049-1059. DOI:10.7519/j.issn.1000-0526.2011.09.001 |
Lalaurette F, 2003. Early detection of abnormal weather conditions using a probabilistic extreme forecast index[J]. Q J R Meteorol Soc, 129: 3037-3057. DOI:10.1256/qj.02.152 |
Lalaurette F. Two proposals to enhance the EFI response near the tails of the climate distribution[OL].www.ecmwf.int/products/forecasts/efi_gaide.pdf. 2003:1-8.
|
Zsoter E, 2006. Recent developments in extreme weather forecasting[J]. ECMWF Newsletter No.107-Spring: 8-17. |
陈静, 陈德辉, 颜宏, 2002. 集合数值预报发展与研究进展[J]. 应用气象学报, 13(4): 497-207. |
陈朝平, 冯汉中, 陈静, 2010. 基于贝叶斯方法的四川暴雨集合概率预报产品释用[J]. 气象, 36(5): 22-39. |
刘家峻, 张立凤, 关吉平, 等, 2010. 集合预报产品在台风麦莎预报中的应用[J]. 气象, 36(5): 21-31. DOI:10.7519/j.issn.1000-0526.2010.05.003 |
Wilks D S, 1995. Statistical methods in the atmospheric sciences[M].
Academic Press, 59.
|
Hersbach H, 2000. Decomposition of the continuous ranked probability score for ensemble prediction systems[J]. Weather and Forecasting, 16: 559-570. |
Mason S J, Graham N E, 2002. Areas beneath the relative operating characteristic (ROC) and relative operating level (ROL) curves: Statistical significance and interpretation[J]. Q J R Meteorol Soc, 128: 2145-2166. DOI:10.1256/003590002320603584 |
 2012, Vol. 38
2012, Vol. 38 
