引言

我国重大社会经济活动往往由中央政府或地方政府筹备并举办，具有规格高、影响大、社会效应强等显著特点，也日益受到多变的气象因素的影响，气象保障服务成为活动的重要组成部分。开展并改进气象服务评估工作是气象服务工作的重要基础工作，也是一项复杂的工作。正是因为气象服务对象和用户的多样性、服务效益的综合性、效益评价的差异性，使得仅从一个方面、一类用户、一种方法难以获得科学、客观的气象服务效益评估结论。我国学者从奥运气象服务满意度CSIWS评估、条件价值评估法、模糊数学、多元回归模型、SVAR模型和专家调查法等多种方法、多角度分析研究服务评估问题^[1-8]。国内运用计量经济学方法研究气象与社会经济的定量关系的成果并不多，但为气象学与社会科学的交叉研究提供了新思路和新方法^[9-12]。高温、雷电、暴雨和大风等高影响天气对北京奥运会、上海世博会和西安世园会等大型的或者长期活动的客流人数、交通状况和安全运行有着很大影响。根据已往综合性世界园艺博览会举办国的经验，举办国都十分关注客流量。把实际客流量作为举办成功与否的重要标志。王小平等^[8]开展了多元回归模型的上海世博会客流量预测分析，比以前常用的渗透率模型和引力模型考虑因素更为全面，但由于只从定性角度分析预测世博参观人数，还存在一定的局限性。

2011年4月28日西安世界园艺博览会(简称世园会)盛大开园，本文以开园日到8月15日的世园会入园客流数量和气象数据为基础构建气象计量经济模型，并运用网络技术和数据库技术建立了业务化气象服务系统。2011年8月底至10月22日，气象部门和世园管理层同时开展了基于网络的业务化应用，运用逐日温度和降水等天气预报信息，结合入园票务政策变化、优惠措施出台、指定日特别活动等信息，联合开展对逐日、未来一段时间和整个运营期的可能入园客流数量的定量预测。该系统的研发应用使得在世园气象服务中不仅开展气象预报服务，还借助智力资源优势将气象信息作为重要信息融入到西安世园指挥运行体系中，从单纯气象要素预报的定性服务向入园客流数量预测的定量服务迈进，开展了世园管理决策层所高度关注的客流预测控制的气象服务工作。

1 2011西安世园会入园客流预测气象服务系统框架

影响世园会入园客流人数的因素主要有非气象要素和气象要素两大类。世园会客流数量预测气象服务系统的设计是以气象计量经济学模型为核心，以计算机网络技术与数据库技术为基础而建立起来的一个气象服务网络平台。计量经济学(Econometric)是综合数学、统计推断及经济理论等工具应用于定量分析的新兴学科，计量经济分析的根本目的是研究结构规律、进行较高精度的预测和实证分析。本文将用计量经济学理论建立的数学模型，对随机误差项的AR(2) 结构、DW统计量、SBC以及AIC等统计变量进行计算，进而应用它们进行入园客流定量预测及分析等。

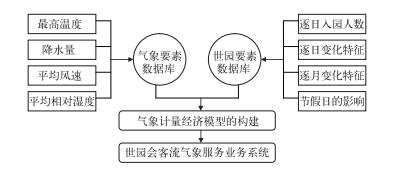
该系统包括气象要素数据库和世园会要素数据库(如图 1)。气象要素数据库包含了基本的温度、降水、风速以及相对湿度等资料；世园会要素数据库包含了入园票检人数、门票销售、团队游客、医疗服务和停车等综合信息。利用未来一段时间的天气预报信息，该系统实现了未来可能入园人数的实时预测。预测信息成为执委会官方了解和掌握世园会客流分布情况的重要参考依据，有利于世园会主办方合理安排交通、餐饮和世园会园区露天娱乐节目表演，以保障西安世园会的有序进行。

2 西安世园会入园客流人数和气象条件分析

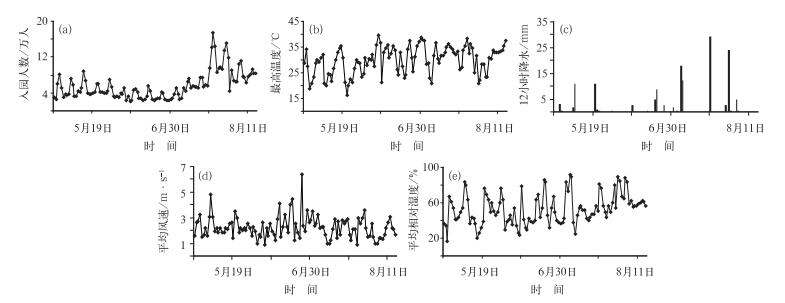
从2011年4月28日西安世园会开园到8月15日的逐日入园客流数量、最高温度、逐12 h降水量、平均风速以及平均相对湿度的逐日时间序列变化如图 2所示。入园客流表现出显著的周期变化特征，以7天为周期而上下波动。其中周六、周日、五一节假日以及暑假是入园客流数量的高峰期。从整体趋势来看，入园人数在4和5月较多，6月入园人数有减少的趋势，但是随着7和8月暑假的来临，入园人数又表现出增加的趋势，尤其是在7月的中下旬达到了一个入园客流数量的顶峰。

逐日最高温度在波动变化中表现出上升的趋势，7—8月高于30℃的天数明显多于4、5和6月，并且最高温度波动变化幅度更小。世园会开园至8月15日这段时间一共有10次明显的降水过程，进入7月以后，降水天数有所增加且降水量有逐渐增多的趋势。4和5月的平均风速波动不大；进入6月以后平均风速变大，波动也增大；7和8月平均风速有所降低，但波动仍然较大。平均相对湿度周期性比较明显，只要出现降水过程湿度都比较高，7和8月的相对湿度维持在较高的水平，波动相对较小。

3 西安世园会入园客流预测气象计量经济模型的构建 3.1 影响入园客流气象因素及非气象变量的设定

入园客流人数P_t。入园人数的统计按照每天检票入园的人数为准，作为模型的因变量。由于入园人数变化较大，所以出现异方差的可能性较大。异方差性违背了回归分析中方差一致性的假设条件，使得参数估计值不是无偏最优的^[13]。本文对入园客流人数取对数log(P_t)，以减少异方差性对参数估计的影响。

时间趋势项t。时间趋势项用以描述入园客流人数随时间的长期变化趋势，这种趋势主要受参观者心理因素以及西安世园会吸引力变化的影响。从图 2可以看出，从4月28日世园会开园到8月15日这段时间，入园客流人数表现出波动上升趋势。

每天的虚拟变量D_it。该变量代表一周内的每天对入园客流人数的影响，其中i=2, 3, …, 7，分别表示周二、周三，…，周日。周一为基础日，当D_it全都为零时，就表示周一。虚拟变量是定性变量，每个虚拟变量的取值只能是0或1。例如，当某一天为周二时，则有D_2t=1，其余D_it=0，以此类推。从图 2可以看出，逐日入园客流人数的变化具有明显的周期性，周一至周五入园人数较少，而周六和周日的入园人数较多。通过引入一周之内每天的虚拟变量，可以很好地反映这种非气象要素引起的逐日变化特征。

月份的虚拟变量M_it。该变量代表不同月份对入园客流人数的影响，其中i=5, 6, 7, 8，分别表示5、6、7和8月。4月为基础月，当M_it全都为零时，就表示4月。虚拟变量M_it的取值只能是0或1，当某一天属于5月的时候，M_5t=1，其余D_it=0，以此类推。从图 2可以看出，不同月份的世园会入园客流人数也有明显的不同，4和5月入园人数较多，而6月的入园人数相对有所减少，7和8月人数有显著的增加。在模型中引入月份的虚拟变量，可以反映非气象要素引起的逐月变化特征。

节假日的虚拟变量V_t。节假日期间入园人数会有所增加，比如每年的五一国际劳动节、暑假以及十一国庆节等时间相对固定的节假日。此外，世园会期间官方举办的一系列打折优惠活动也可以看成是该虚拟变量，在这些节假日期间V_t=1，其余时间V_t=0。节假日虚拟变量的引入，可以使模型的设定形式更加准确。

气象要素变量。天气预报已经成为人们做出出行决策的重要判断信息。每日天气状况不仅影响园区树木花卉的生长，也对人们出行有显著影响。游客一方面根据预报做出预判断，另一方面根据实况做出现实选择，这一因素会对客流量产生影响，特别是预报的准确性，会直接影响游客对是否游园的判断。在模型中的设定有W项(即预报信息)和W_t-1项(即前一天的天气实况)，当用模型进行客流预测时，既考虑了未来天气预报的影响，又考虑了现在天气实况的影响。为分析世园会期间一些重要的气象要素影响入园客流人数的定量大小，模型引入的气象要素包括最高温度(T_t)、降水的虚拟变量(R_t)、平均风速(W_t)，以及平均相对湿度(H_t)4个变量。

3.2 入园客流预测模型形式及其参数估计

由3.1节设定的变量可知，影响世园会入园人数的因素主要有非气象要素和气象要素两大类。4—6月这段时间，最高温度、降水、风速以及相对湿度都是影响入园客流的气象因素，综合考虑这些因素，建立第一个模型：

$ \log ({P_t}) = c + \alpha t + {\beta _i}\sum\limits_{i = 2}^7 {{D_{it}}} + \gamma \sum\limits_{i = 5}^8 {{M_{it}}} + {\lambda _i}\sum {{V_{it}}} +\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;m{T_t} + n{R_t} + p{W_t} + q{H_t} + {\varepsilon _t} $

其中，c，α，β_i，γ_i，λ_i，m，n，p以及q为需要估计的模型参数，ε_t为随机误差项。第一个模型参数估计结果见表 1所示。常数项非常显著，时间趋势项为很小的负值但不显著。周二和周三的系数为负值，而周四、周五以及周末两天的系数都为正值，但只有周五、周六和周日的系数非常显著。参数估计结果说明，相对于周一来说，周二和周三这两天的入园人数会分别减少8.5%和3.9%，而周五至周日这3天的入园参观人数会显著地分别增加22.9%、58.5%和53.8%。相对于4月来说，5月的入园人数增加45.8%，6月的入园人数增加14%，但t检验不显著。4类气象要素对入园人数都有负面影响，其中降雨和平均风速的系数t检验显著，即发生降雨的天气将使入园人数减少15.2%，平均风速每增加1 m·s^-1将使入园人数减少5.4%。模型的拟合优度为0.87，不是很高。DW统计值为2.43，说明模型的随机误差项存在负的一阶自相关性。

由以上分析可知，第一个模型的设定形式不够完整，使得模型的随机误差项存在负的一阶自相关性。自相关性的存在使得模型参数估计值不是无偏最优的，参数估计值也可能是不合理的，例如最高温度T_t和平均相对湿度H_t两个气象要素对入园人数的影响t检验不显著。因此，模型设定形式需要进一步完善。为了消除自相关问题，在第一个模型的基础上引入随机误差项的自回归结构(AR)，考虑到人们通常根据未来气象预报信息做出出行决策，以及天气预报的准确性问题，确定了二阶自回归结构AR(2) 的形式。第二个模型的完整形式如下：

$ \begin{array}{l} \log ({P_t}) = c + \alpha t + {\beta _i}\sum\limits_{i = 2}^7 {{D_{it}}} + \gamma \sum\limits_{i = 5}^8 {{M_{it}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _i}\sum {{V_{it}}} + m{T_t} + n{R_t} + p{W_t} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;q{H_t} + ({\phi _1}{\varepsilon _{t - 1}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\phi _2}{\varepsilon _{t - 2}} + {\alpha _t}) \end{array} $

其中，(${\phi _1}{\varepsilon _{t -1}} + {\phi _2}{\varepsilon _{t -2}} + {\alpha _t}$)为随机误差项的AR(2) 结构，$\phi$₁和$\phi$₂为需要估计的参数，α_t为随机白噪声过程。第二个模型参数估计结果见表 1所示。可以看出，拟合优度(R²)提高到0.93，说明模型的拟合能力有很大的提高。DW统计值为2.01，自相关性被消除。节假日造成入园人数显著地增加28.3%。与第一个模型相比，每一天和月份的虚拟变量的系数值改变不大，但影响入园人数显著的气象因子为最高气温和降水。最高气温每升高1℃，入园人数将减少1.2%。发生降雨的天气，入园人数将减少14.4%。

第二个模型在对实际值的拟合能力上有较大的提高，也消除了异方差性对参数估计的影响。事实上，由于气象要素变化连续性，当天的气象要素(最高气温、降雨、风速和湿度)对次日的入园人数有较大的影响。为了让模型的设定形式更加合理，在第二个模型的基础上引入气象要素的一阶滞后项，第三个模型的完整形式如下：

$ \begin{array}{l} \log ({P_t}) = c + \alpha t + {\beta _i}\sum\limits_{i = 2}^7 {{D_{it}}} + \gamma \sum\limits_{i = 5}^8 {{M_{it}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _i}\sum {{V_{it}}} + m{T_t} + n{R_t} + p{W_t} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;q{H_t} + {m_1}{T_{t - 1}} + {n_i}{R_{t - 1}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_1}{W_{t - 1}} + ({\phi _1}{\varepsilon _{t - 1}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\phi _2}{\varepsilon _{t - 2}} + {\alpha _t}) \end{array} $

其中，T_t-1，R_t-1，W_t-1和H_t-1分别为最高温度、降雨、平均风速和平均相对湿度的一阶滞后项，m₁，n₁，p₁和q₁为对应的需要估计的参数。模型参数估计结果见表 1。节假日期间，入园人数将增加32.7%，t检验十分显著。与周一相比较，周二和周三的入园人数有所减少，而周五至周日的入园人数将十分显著地分别增加22.9%、55.8%和47.3%。与4月相比较，5月入园人数显著地增加47.4%，6月系数t检验不显著。引入气象要素的一阶滞后项之后，当天的气象要素对世园会入园人数的影响不具有统计显著性，而前一天的最高温度(T_t-1)升高1℃，当天入园人数将减少1.7%，前一天的平均风速(W_t-1)增加1 m·s^-1，当天的入园人数增加6.4%。模型的拟合优度(R²)为0.93，DW统计值为1.94，自相关性被消除。

进入7月以后，西安迎来了高温多雨的天气。高温和降水是影响世园会入园客流数量的主要因子，而风速和相对湿度的影响并不显著。为感谢和回馈广大市民，西安市委、市政府决定，从7月开始向每户西安市民发放一份市民礼包，礼包发放和使用都有较为严格的时间限制，这为业务系统预测可能入园客流人数增加了很大的不确定性。针对4至8月的入园客流情况，本文只考虑高温天气和降水两个气象因素，并且在模型中引入“大礼包”这个虚拟变量对模型参数进行重新计算。

4—8月这个时间段的模型参数估计与显著性检验如表 2所示。由模型3的参数估计值可知，与非节假日相比，节假日的到来将会使得入园客流人数增加50.1%；与周一相比，周六和周日的入园人数将会显著增加47.3%和41.3%；高温天气和降水天气对入园客流人数的影响十分显著。当发生高温和降雨的天气时，入园客流人数将分别减少15.7%和7.73%，而前一天的高温天气会使得次日的入园客流人数减少12.7%。

4 西安世园会入园客流预测气象计量模型评估及其业务化应用 4.1 世园会入园客流预测气象计量模型的评估

通过对比表 1中的模型2可以发现，模型3稍微有所改进。引入气象要素的一阶滞后项之后，造成当天气象变量的系数t检验变得不显著。为剔除大礼包派送等不确定性因素的影响，本文仅对表 1中的模型2进行预测能力评估，并用该模型对入园客流人数开展预测，讨论其业务运用的可行性。将4月28日至6月30日的入园客流人数时间序列分为两部分。6月15日之前的数据为第一部分，用来估计模型的参数，并检验模型对数据的拟合水平。6月16日之后的数据为第二部分，用来检验模型的实际预测能力。

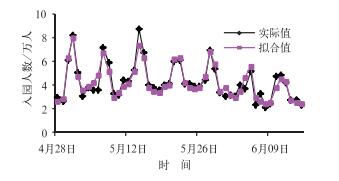
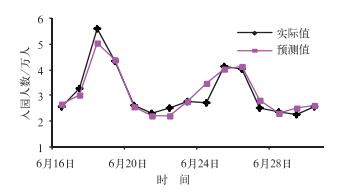
图 3为模型的拟合值与实际值的比较，拟合值与实际值十分吻合，表明模型中所引入的变量科学合理，模型能很好地模拟世园会入园客流人数的逐日和逐月变化特征。将6月15日之后两周的气象要素信息带入模型，对未来两周的可能入园客流人数展开预测。从图 4的结果可以看出，模型比较准确地预测了未来两周的入园客流人数，表明模型的实际预测能力较强，可以投入实际的业务化运用。

为了进一步研究模型的预测时效性，需要对比分析模型在不同时间长度上的预测准确性。图 5为预测时间长度分别为1~7 d和8~15 d时，模型预测误差指标的对比分析。当预测时间长度为1~7 d时，预测绝对误差为2000人，预测相对误差为6.05%，系统偏差比例为4.78%。当预测时间长度为8~15 d时，预测绝对误差为2043人，预测相对误差为6.98%，系统偏差比例为5.47%。可见，模型对1~7 d的预测准确性略高于8~15 d的预测结果。

4.2 世园会入园客流预测模型的业务化服务系统

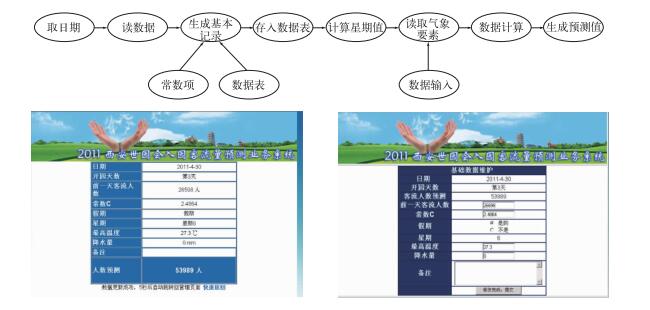
西安世园会入园客流人数预测系统的核心是表 2中的模型3。由于模型中考虑了输入较多的相关因子，在业务化系统设计中既要充分考虑系统的可维护性，又要考虑世园执委会用户群和气象部门业务人员每日业务化应用的便利，使用ASP.NET+Access技术设计业务系统，程序设计使用Microsoft Visual Studio 2005，并采用B/S结构，链接在世园气象服务网(5月与世园会官方网站链接)上运行、管理和日常维护(图 6)。经过8月底为期10 d的双方测试后，正式投入双方日常运行工作中，世园执委会投资策划部门用其对未来3日的散客、团队客等客流进行预测及控制工作。

运用已经建立好的业务系统对2011年8月16日至10月22日区间段的可能入园人数开展定量预测分析。西安市1970—2009年历史同期气候特征见表 3，依据此表对8月16日至10月22日世园会开园期间的天气状况进行经验判定。

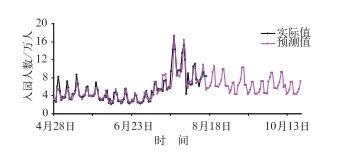
利用西安市1970—2009年历史同期气候特征，将未来天气状况的经验判定结果带入业务系统中，经过计算得到8月16日至10月22日时间段的逐日可能入园散客客流数量，以及4月28日至10月22日整个世园会运营期间的入园散客总人数。由图 7可见，8月下旬的入园客流人数呈减少趋势；但在9月和10月上旬的入园客流将有所增加。业务系统预测结果表明4月28日至10月22日整个世园会运营期间的入园散客总人数约为1032万人。8月，气象部门和世园执委会相关部门，依据开园以来的连续数据分析，散客人数所占总人数的比例约为55%~65%，提前两个月计算得到世园会入园客流总人数逾1600万人。这个预测数据与10月22日官方公布的实际入园人数1573万人很接近。

通过对4月28日至9月11日预测值与实际值的统计计算，预测值与实际值之间的相关系数为0.959，通过了0.01的显著性水平检验。将每一天的实际客流量与前一天的客流量的差值视为客流变化，其结果为增加或减少；将当天预测客流量与前一天的客流量的差值视为客流趋势预测。根据预测结果统计，趋势预测准确率为72.6%。

5 西安世园会入园客流预测气象服务主要结论和讨论

复杂多变的气象因素对2011年西安世园会的参观人数有重大的影响。开展气象因素影响入园客流人数的定量分析，有助于进一步加深认识气象与社会的关系，可以更加及时地开展气象保障服务，促进世园会的平稳持续进行。采用计量经济学方法，以最高温度、平均风速、平均相对湿度为定量解释变量，以降水、节假日、每一天、月份为虚拟解释变量，引入随机误差项的AR(2) 结构，通过逐步优化的建模思想，构建了气象因素与入园客流人数的计量经济模型，能很好地模拟世园会入园客流人数的逐日和逐月变化特征，能比较准确地预测未来两周的可能入园人数和总人数。主要结论如下。

(1) 模型很好地解释了节假日、每一天以及不同月份对入园客流人数的定量影响。相对于周一来说，周二至周四的入园人数没有统计上的显著性差别，而周五至周日的入园人数会显著性地增加。相对于4月，5月的入园人数显著地增加41.5%；6月入园客流人数减少3.39%；7月的入园客流人数增加18.0%；而8月的人数减少13.0%。

(2)2011年4—6月期间，四类气象要素对入园客流人数都有负面影响。最高温度和降雨的系数t检验显著。最高气温升高1℃，入园人数将减少1.2%，如果发生降雨，入园人数将减少14.4%。7—8月期间，高温天气和降水天气对入园客流人数的影响十分显著。当发生高温和降雨的天气时，入园客流人数将分别减少15.7%和7.73%，而前一天的高温天气会使得次日的入园客流人数减少12.7%。

(3) 利用西安市1970—2009年历史同期气候特征，将未来天气状况的经验判定结果带入该业务系统中，8月底即提前两个月，经过计算得到世园会运营期间的入园散客总人数约为1032万人，预测世园会入园客流总人数逾1600万人，与2011年10月22日官方公布的实际入园人数约1573万人很接近。

(4) 客流预测气象计量经济模型和客流预测气象服务业务系统能很好地模拟世园会入园人数的逐日、逐月变化特征，能比较准确地预测未来15 d的入园人数，并且对1~7 d的预测准确性略高于8~15 d的预测结果。虽然模型和业务系统能较好地模拟入园客流人数的逐日、逐月变化特征，但对个别天数的模拟值存在一定的偏差。主要原因可能与在西安世园会举办期间，组委会和执委会官方不定期“大礼包派送”等激励政策和公益活动，或不同类门票的到期时间不同有关，这些构成客流预测不确定性影响因素。

在模型的实际运用中，模型预测的准确性依赖于温度、降水、风速和相对湿度等气象因素的预报准确性。在模型中的设定有W_t项(即预报信息)和W_t-1项(即前一天的天气实况)，当用本文的模型进行客流预测时，既考虑了未来天气预报的影响，又考虑了现在天气实况的影响。游客一方面根据预报做出预判断，另一方面根据实况做出现实选择，这些因素会对客流量产生影响，特别是预报的准确性，会直接影响游客对是否游园的判断，但情况会比较复杂。游客根据预测做出预判断，预报准确率越高，游客对未来预报信息越信赖。实践应用时特别强调中短期预报的准确性，进一步增加预报信息W这一项的置信度，提高对入园客流人数中短期预测的准确率。对复杂和不确定因素的影响还需要继续深入研究。