引言

目前常用的实时气温质量控制方法的主要思想是利用气候学分区、地理分区和站点历史极值等数据对实时气温设定静态阈值，首先判断某测点温度是否在静态阈值范围内，超出阈值设定的测点即判为疑误数据，然后，对符合阈值范围内的数据再进一步做连续时间序列和空间临近参考点的对比，从而判断出该站点气温的最终质量^[1-8]。这种方法形式简洁并且运行效率很高, 是目前普遍应用于实际操作中的一种经验检验方法。但是这种方法也存在一些缺点：(1) 不是真正意义上的实时控制方法，质量判别前需要根据经验和历史极值人工设定参考值；(2) 对中小尺度离散的气温判断较为有优势，但是在大尺度离散的气温分析判断上，准确性较低；(3) 极端天气过程误判率较高；(4) 地理边界点判断较为困难。

k-means算法^[9-10]是数据挖掘中聚类方法^[10-13]的一种，聚类就是一个将数据集划分为若干簇或类的过程，通过聚类使得同一类内的数据对象具有较高的相似度。

本文首先根据实时气温分布的特点，探讨了k-means聚类方法运用于实时气温质量控制的适用性，提出了相关的计算方法和定义，建立了相应的气温质控流程，并用实例加以展示，最后与传统气温质量控制方法进行了对比。

1 k-means算法 1.1 k-means算法的适用性分析

气温是气象要素的一个重要属性，如果从地理分布上看，各测点的实时气温分布比较散乱，缺乏分布规律。但是我们可以根据大气运动的特征，将区域内气温值相近的站点聚集成若干个足够小的子聚集区，使得子聚集区内单点气温的变化趋势与其所属聚集区的整体变化趋势具有同步性。从另一个方向解释，单点气温变化明显背离于其所属的足够小的子聚集区的整体气温变化趋势，且背离趋势加剧时，可判定该点属于气温异常点。

k-means方法适用于处理数值属性数据集，能对大量数据根据属性进行高效的分类。因此，可将k-means方法应用于气温属性的聚类划分，然后再对聚类中的气温异常点进行判别。

1.2 相关定义和概念

设C={p₁, …, p_n}为区域内n个离散点的气温属性集合，则将气温的欧式距离作为各离散对象间距离的度量方法，定义为：

$ d\left( {{p_i}, {p_j}} \right) = \sqrt {{{\left( {{p_i}-{p_j}} \right)}^2}} \;\;\left( {{p_i}, {p_j} \in C} \right) $

(1)

式中，d(p_i, p_j)为两点温度差的绝对值。

设μ为群中心，即群的质心，是群内所有点值和的平均：

$ \mu = \frac{1}{n}\sum\limits_{i = 1}^n {{p_i}} $

(2)

σ为标准差，反映了群内个体间的离散程度，定义为：

$ \sigma = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{p_i}-\mu } \right)}^2}} }}{n}} $

(3)

θ_i为离群率，反映的是某个体与群中心的离散程度：

$ {\theta _i} = \left| {\frac{{{p_i}-\mu }}{\sigma }} \right| $

(4)

δ_i为离群速度，反映的是个体偏离中心的速度：

$ {\delta _i} = \left| {\frac{{\Delta {\theta _i}}}{{\Delta t}}} \right| $

(5)

式中，Δθ_i表示两个相邻时间离群率的差，Δt表示时间差，δ_i是有单位的非负值，它的数值越大表示偏离中心的速度越快，数值越小表示与中心的移动速度越接近。

1.3 k-means算法过程

k-means算法属于局部最优的聚类方法中应用最为广泛也是最高效的一种，通过指定聚类个数k，把含有n个数据的数据集C划分k个聚类(C₁, C₂, …, C_k)，利用迭代方式，最终使每个聚类中的数据点p到该聚类中心的距离最小^[14]。k-means算法的主要处理过程为：

输入：聚类个数k，n个数据的数据集。

输出：k个聚类。

(1) 从n个数据对象中任意选取k个对象作为初始聚类中心。

(2) 分别计算每个对象到各个聚类中心的距离，把对象分配到距离最近的聚类中。

(3) 所有对象分配完成后，重新计算k个聚类的中心。

(4) 与前一次计算得到的k个聚类中心比较，如果聚类中心发生变化，转(2)，否则转(5)。

(5) 输出聚类结果。

k-means算法采用误差平方和准则函数来评价聚类性能，具体定义如式(6) 表示:

$ E = \sum\nolimits_{i = 1}^k {\sum\nolimits_{p \in {C_i}}^{} {{{\left\| {p-{m_i}} \right\|}^2}} } $

(6)

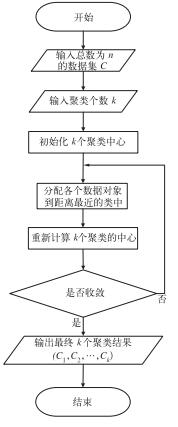
式中，p为对象空间中一个数据对象，m_i为聚类C_i的均值，该函数旨在使生成的聚类结果集尽可能的紧凑和独立。k-means算法流程图如图 1所示。

1.4 离群点

此外还需要了解离群点的概念：一个离群点是这样的数据点，基于某种度量，该数据点与数据集中其他的数据点有着明显的不同^[15]。在基于距离的离群点判别中，假设数据集中一个对象与均值的偏差大于或等于某个阈值时，则认为该对象就是一个离群点^[16]。本文算法对离群点的判别，主要以单点气温与其所属聚类中心的离群率θ_i和离群速度δ_i的综合考量作为判断的参考值。

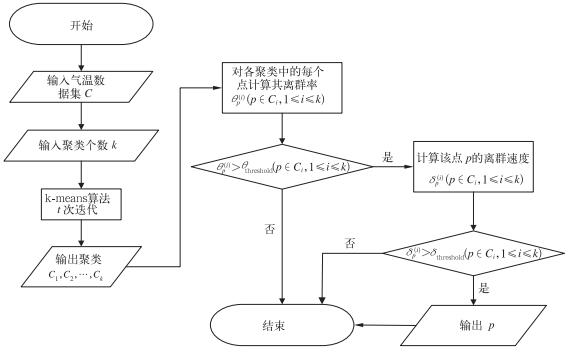
2 气温质量控制算法流程及性能分析 2.1 算法流程

结合前文所述概念和定义，气温质量控制算法实质上是相似温度测点的聚类、离群率判别和离群速度判别3个步骤的综合，主要流程如下(如图 2所示)：

输入：n个气温点的实时气温数据集C，聚类个数k，其中p(p∈C)为气温数据集C中的某个气温点；

输出：空值或p；

(1) 数据集C经过t次k-means迭代，输出k个聚类(C₁, C₂, …, C_k)；

(2) 对聚类(C₁, C₂, …, C_k)中所有气温点p，计算其离群率θ_p⁽ⁱ⁾(p∈C_i, 1≤i≤k)；

(3) 判断θ_p⁽ⁱ⁾>θ_threshold(p∈C_i, 1≤i≤k)，是转(4)，否转(7);

(4) 计算p点的离群速度δ_p⁽ⁱ⁾(p∈C_i, 1≤i≤k)；

(5) 判断δ_p⁽ⁱ⁾>δ_threshold(p∈C_i, 1≤i≤k)，是转(6)，否转(7)；

(6) 输出p点，该点作为气温异常点；

(7) 结束算法。

2.2 算法复杂度

对于大数据集，该算法是相对高效率的。算法通过k-means、离群率判别和离群速度判别的这三个步骤，根据气温点总量n，聚类个数k和迭代次数t，可知算法总的复杂度为O(nkt)+O(n)+O(n)，在忽略非主要项后，整体复杂度约为O(nkt)。

2.3 关于k值的选择

算法流程中，聚类个数k的值是需要预先输入的，因此k值的选择会影响最终的判定效果。在气温质量控制算法中，k值并没有精确的计算方法，一般都是根据该区域内测站的水平或者垂直分布情况来进行人为估计。

这里给出一种基于水平分布的k值期望算法。设n_e表示期望测站数量，它是一个根据水平尺度大小预设的经验值，为正整数，表示的是该区域内测站在均匀分布的假设下，人们对测站总数量的最佳期望值，则聚类个数k为：

$ k = \left[{\frac{n}{{{n_{\rm{e}}}}}} \right] $

(7)

式中，n是实际测站数量，k是n和n_e比值的向上取整。当n≤n_e时，k=1；当n_e不变，k随着n的增加而增大。

3 运行实例

将山东省123个国家级自动气象站固定以0~122的数字进行编号，将2011年7月28日00和01时的观测气温数据为输入数据集，按照基于水平分布的k值期望算法，预设期望测站数量n_e=100，计算出聚类个数$k = \left[{\frac{{123}}{{100}}} \right] = 2$作为输入值，经过k-means算法迭代收敛后，生成聚类cluster0和cluseter1。

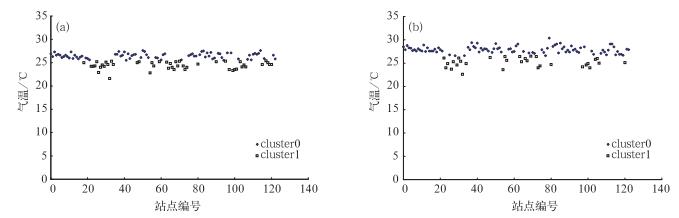
为方便显示，以编号为横坐标，气温值为纵坐标，28日00和01时的气温聚类分布如图 3所示，聚类统计信息如表 1和2所示。

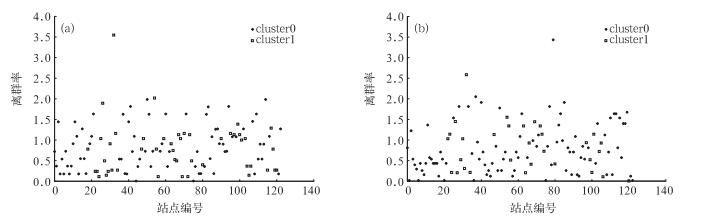
经过聚类后，根据算法流程，应当计算各点的离群率，仍以站点编号为横坐标，以离群率为纵坐标，显示00和01时的离群率分布图，如图 4所示。

我们假设00时的各测站气温全部正确，并以其为参照值来判断01时的气温质量，并假设离群率阈值θ_threshold=2，同时，为了方便表述，我们以五元组(编号, 时次, 聚类, 气温, 离群率)指示该点的状态。从图 3b和图 4b中可以看出，01时仅点(32, 01, cluster1, 22.6℃, 2.583199) 和点(79, 01, cluster0, 30.4℃, 3.430813) 的离群率超过阈值2，因此，此两点将进入下一步离群速度的判断，其他点判断为正确，不再进行下一步判断。

要计算离群速度，需要追溯至上个时次，我们从图 3a和图 4a中找出编号为32和79的测温点在00时的状态，分别为(32, cluster1, 21.6℃, 3.543865) 和(79, cluster0, 26.4℃, 0.185621)，并假设离群速度阈值为δ_threshold=2 h^-1。可以看出，编号为32的测温点的离群速度达$\left| {\frac{{2.583199-3.543865}}{{1\;{\rm{h}}}}} \right| = 0.960666\;{{\rm{h}}^{-1}} $，小于阈值2 h^-1，从而属于正确点，通过质控检测；而编号为79的测温点的离群速度达$\left| {\frac{{3.430813-0.185621}}{{1\;{\rm{h}}}}} \right| = 3.245192\;{{\rm{h}}^{-1}} $，大于阈值2 h^-1，因此该点为错误点。

我们再从经典直观的角度解释该判断过程，在01时，虽然(32, 01, cluster1, 22.6℃, 2.583199) 与其聚类中心25.1032℃的距离达|22.6℃-25.1032℃|=2.5032℃，但是通过追溯00时的状态发现，该点的变化始终与其所在聚类中心温度的变化保持相对同步，因此该点可判定为正确点。反之，(79, 01, cluster0, 30.4℃, 3.430813) 不但与其聚类中心温度距离较大，达|30.4℃-27.913℃|=2.487℃，且该点仍然呈现快速远离中心温度的趋势，因此判定该点属于错误点。

需要指出的是，实例中离群率阈值θ_threshold和离群速度阈值δ_threshold的设置仅为演示数值，实际工作中应当根据测温站点分布平均密度等条件来做相应设置，并可根据实际情况做动态的调整；而且，站点离群速度的判断是在上一个时次该点气温值为正确的前提下进行的，如果该点气温值持续多个时次异常，那么当前时次的离群速度作为异常点的判定标准就不适用，在此种情况下，可以应用传统质控方法中的时间一致性检查方法^[1]作为离群速度的替代判定方法。

4 小结

本文提出了一种高效的实时气温质量控制算法，该方法通过k-means算法聚类、离群率判别和离群速度判别三个步骤，对区域内所有观测点的气温测值进行动态的质量检测。该算法的复杂度较低，适合大输入数据集的计算。

该方法与传统质控方法相比，具有一定的优势。首先，传统算法的区域划分主要是根据站点所处的水平经纬度或者海拔高度，利用其所属的气候学区域或地理垂直分层等进行人为的划分，而一经划定，就无法再更改，缺乏灵活性。而k-means算法的每一次质量控制过程，站点都通过彼此间温度的相似性自动分区，因而灵活性较高。其次，传统质控算法对温度合理值判定是以预设温度绝对阈值的方式，其参考值主要是区域气候极值或台站气候极值，这种方式往往会造成对于局地天气或者极端天气过程的误判。而k-means算法关于阈值的思想是判断单点与整体的偏差的允许程度，是当前时刻站点气温个性与范围内气温共性的比较，因此，它的设定不需要参考极值，更具实时性和科学性。

与此同时，通过算法实例可以看出，k参数、离群率阈值和离群速度阈值都是直接影响最终质控结果的主要因素，因此，如何合理的设置参数值，将是今后工作的研究重点。