引言

降水引起的洪涝事件，给人民的生产生活常常带来极大损失。而短期气候预测尤其是降水预测仍是一个挑战性的难题。Stockdale等^[1]用一个全球海气耦合环流模式试做提前6个月的气候预测，认为尽管置信水平还不是很高，但对于气候预测而言已经是一个相当不错的结果。Wang等^[2]用多模式集合气候预测系统做出东亚和西太平洋区域夏季降水的预测，考察了距平百分率和误差距方差，发现6个模式的集合的回报技巧由原来的0.12提高到0.22。Liu等^[3]运用区域气候模式对中国夏季降水做了10年的预报试验，发现该模式对我国汛期降水具有一定跨季度预报能力，对西部、东北、长江下游等地有较强的预报能力。尽管如此，受限于模式分辨率等因素，模式预测的效果仍然未能超过统计方法预测。Colman等^[4]选择1—2月的北大西洋海温作为预测因子，采用线性回归模型对7—8月的欧洲降水作了预报，结果表明预报值与观测值相关系数达到0.4。国内降水预测方面，Wu等^[5]运用奇异谱分析(SSA)对降水量序列进行前处理，用模块化人工神经网络预测长江流域降水量，在季节预测和逐日预报中较其他前处理方法均取得了理想的结果。Zhang等^[6]运用一种基于奇异值分解的短期气候预测模型对华北和江淮区域夏季降水做了预测，认为预报值和实况值在大多数年份有较高的相关系数，误差稳定，趋势预报的效果较好，但异常值的误差也是显著的。但总体而言，夏季降水预测水平还不高，难以实现在全国大部分地区做出准确预测。目前我国汛期降水的气候趋势预测准确率在65%左右。

海温和高原积雪、冻土等因子在业务实践中，已广泛地应用于对中国夏季降水的预测。Huang等^[7]指出，处于发展(衰减)阶段的ENSO事件往往造成江淮流域降水偏多(偏少)，而黄河流域、华北地区和江南地区降水偏少(偏多)。龚道溢等^[8-9]分析了春季北极涛动(AO)的变化对随后夏季长江中、下游地区降水的影响，发现近百年的5月北极涛动指数与研究的10个站的夏季平均降水相关系数高达-0.39，超过0.01的显著性水平检验。较强的AO异常对降水的影响更明显，而较弱的AO与降水异常的对应关系并不显著。吴统文等^[10]指出青藏高原多雪年夏季长江及江南北部降水可偏多1~2成，华北和华南的降水则偏少1~3成；少雪年夏季江淮流域及湘、黔地区少雨，华北和华南多雨。Wang等^[11]利用青藏高原46个气象站的最大冻土深度观测资料、全国160站的降水资料和NCEP/NCAR资料对青藏高原冻土的季节性冻融过程进行合成分析，发现最大冻土深度与中国7月降水有三条显著相关带，雨带的分布与中国夏季平均雨带相吻合。

上述研究表明，降水作为大气环流的产物，必然有着自身的演变规律，也和其他外强迫和相关因子之间存在着联系。除数值模式模拟预测外的预测方法，把这两种过程有机地结合起来是提高预测水平的有效途径。本文探索运用奇异谱分析-最大熵预报方法分析、预测其内在演变规律，应用最优子集回归方法分析降水和其他气象因子之间的联系，两者结合起来对中国汛期降水进行预报试验，以期探索一种有效的、可用于业务操作的预报途径。

1 资料与方法

本文采用的降水资料来自国家气候中心发布的全国160个气候基准站1951—2004年6—8月逐月降水资料，以6—8月为夏季降水量。并选取前一年12月至当年3月北大西洋涛动(NAO)指数、北极涛动(AO)指数、厄尔尼诺-南方涛动(ENSO)指数、青藏高原积雪深度、青藏高原最大冻土深度作为预测因子。

运用奇异谱分析-最大熵方法检测和预测降水自身的变化规律；在前述的因子中选择建立最优子集回归方程用于分析降水和其他因子的关系，以之预报降水中受强迫因素的部分。最后，根据线性集成将两种方法结合起来形成最终的降水量预测结果。由于每个站的自身变化规律的差异以及各站点和前一段中所列因子之间的相关不同，因此，各个站建立的SSA-MEM、最优子集回归方程及其最后的集合方程也就各不相同。

由于奇异谱分析(SSA)不需要波形信号为正弦的假定，且对功率谱信号有放大作用而特别适合于非线性系统进行时频分析^[12]。另外，传统的谱分析只考虑有限的观测时间内的信息，没有考虑观测时间外的信息，采取数据加窗的处理方法，人为改变了实际信息。而最大熵谱估计(MESA)基于信息的最大不确定性，将有限的观测值外推为无穷序列，外推的方法类似于自回归模型。最大熵谱估计尤其适合于处理类似于气象观测这种长度较短的数据记录。同时，最大熵谱估计也是一种非线性谱分析方法。将奇异谱分析与最大熵谱估计结合起来，更适合于对气象要素的分析和预测。简要地说，奇异谱分析-最大熵预报方法基本步骤如下。

将原始序列标准化，取定滑动窗口长度M，得到时间滞后排列矩阵：

$\begin{array}{l} X = \left[ {\begin{array}{*{20}{c}} {{x_1}} & {{x_2}} & \cdots & {{x_{i + 1}}} & \cdots & {{x_{N,m + 1}}}\\ {{x_2}} & {{x_3}} & \cdots & {{x_{i + 2}}} & \cdots & {{x_{N,m + 2}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {{x_M}} & {{x_{M + 1}}} & \cdots & {{x_{i + M}}} & \cdots & {{x_N}} \end{array}} \right]=\\ \quad \quad \left[ {\begin{array}{*{20}{c}} {{X_{1,0}}} & {{X_{1,1}}} & \cdots & {{X_{1,N,M}}}\\ {{X_{2,0}}} & {{X_{2,1}}} & \cdots & {{X_{2,N,M}}}\\ \vdots & \vdots & \vdots & \vdots \\ {{X_{M,0}}} & {{X_{M,1}}} & \cdots & {{X_{M,N,M}}} \end{array}} \right] \end{array}$

(1)

对式(1) 计算滞后自协方差矩阵，用类似于经验正交函数分解(EOF)的方法提取时间EOF(T-EOF)和时间主成分(T-PC)。T-EOF是时滞矩阵的特征向量E^k，T-PC相当于E^k所反映的时间演变型在原序列的x_i+1，x_i+2，…，x_i+m时段的权重，由下式确定：

$a_i^k = {X_i} \cdot {\mathit{\boldsymbol{E}}^k} = \sum\limits_{j = 1}^M {{x_{i + j}}} E_j^k,0 \le i \le N - M$

(2)

由第k个T-PC和T-EOF重建x_i^k：

$x_i^k = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{M}\sum\limits_{j = 1}^M {a_{i - j}^kE_j^k,M \le i \le N - M + 1} }\\ {\frac{1}{i}\sum\limits_{j = 1}^i {a_{i - j}^kE_j^k,1 \le i \le M - 1} }\\ {\frac{1}{{N - i + 1}}\sum\limits_{j = i - N + M}^M {a_{i - j}^kE_j^k,N - M + 2 \le i \le 2} } \end{array}} \right.$

(3)

通过识别趋势项和周期项确定前几个解释方差贡献大的k。提取出的T-PC虽不严格是正弦波，但非线性项已得到平滑，具有较高的可预报性^[7]。用最大熵谱估计中类似于AR模型的方法，采用Burg递推公式，对T-PC做出预报。AR模型阶数的选择采用最终预测误差(FPE)准则。将预报出的前k个T-PC与T-EOF结合即得到原始序列的预报，结合方式类似于式(3) 中第三式。奇异谱分析-最大熵预报方法具体原理参见文献[13-14]。

气候变化具有向外源适应的特征。对于跨季节的气候预测，必须寻找具有“缓变”特征的外强迫源，在此基础上，进一步分析这些外强迫源和气候之间的关系，进而对气候变化做出预测。已有的研究表明，海温是气候预测的一个强的“信号”，高原积雪等因子经过实践也表明对东亚夏季降水具有较好的指示意义。尽管这些因子和我国夏季降水之间并非线性关系。但多元回归分析仍然可以“回归”出中国夏季降水和海温、高原积雪等外强迫因子之间的基本信息，从而预测出中国夏季降水的部分信息。尤其逐步回归方法由于既考虑了因子和预报对象之间的关系，也考虑了因子之间的相互关系，且运算简单，适合于从许多因子中挑选出使方程最优残差最小的因子。但也存在着出现局部最优的情况。因此，相对而言，最优子集回归具有计算速度快、误差小的特点，作为回归的首选模型。基本思想是采取合理途径、穷尽所有预测因子的搭配，找到最优的回归方程^[15]。

最优子集回归方法是从所有可能的回归中确定出一个效果最优的子集回归，确定的方法是双评分(CSC)准则，CSC值定义为数量评分和趋势评分之和，CSC评分值越小，回归方程越好。更为具体的原理和方法参见相关文献[15-18]。

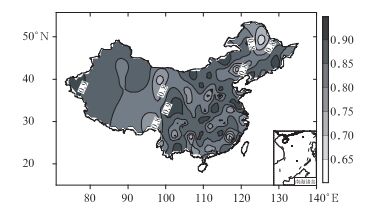
2 回报结果及其检验

图 1给出了1961—2000年全国降水量实况值与试报值距平相关系数分布图。从图中看出，所有160站的距平相关系数均通过了0.01的显著性水平检验, 平均距平相关系数达到0.85。相关系数相对较高的地区为青藏高原地区，新疆中部，四川、重庆等地，内蒙古中部，黑龙江中部、吉林东部，江苏沿海地区，浙江北部、安徽中西部及广西、贵州中西部等地区，相关系数超过了0.8(超过0.01的显著性水平检验)。总体而言，西部地区及江淮地区的相关系数水平较高。

3 试报结果检验

一般地，Brier评分(BS)小于20%表明预报效果较好。使用上述方法，对2001—2004年进行试报，并对结果进行BS评分。结果显示，除内蒙古西部、东北北部等局部地区BS评分大于20%外，其余大部分地区BS评分均小于20%。结果表明在全国大部分地区的预报结果均较为理想。需要指出的是取得的高BS可能与试报时间(4年)较短有关。

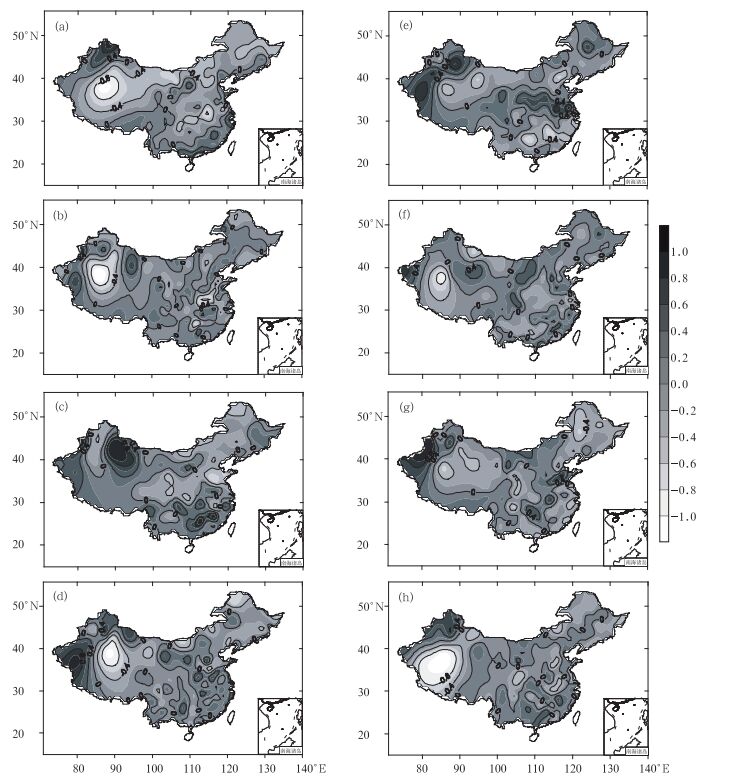
为进一步检验该方法，将上述方法应用到逐年的夏季降水预测。图 2给出了2001—2004年夏季降水量距平百分率实况值和预测值。2001年夏季(图 2a)，沿海地区自渤海湾至广西南部、青藏高原东南部、河套地区北部及内蒙古中部、新疆北部等局部地区降水为正距平，其余大部分地区降水显著偏少，其中青藏高原北部有一低值中心。从预测图(图 2e)上看，全国大部分地区的降水负距平均得到了体现，青藏高原北部以及江淮流域内的低值中心也被成功预测。除江苏中部、浙江中部及广东中部局部地区外，其余大部分沿海地区的预测结果与实况一致。误报主要集中在西北地区东部和东北中部地区。

2002年夏季(图 2b)，由黄河流域与长江流域之间大部分地区向东北延伸至华北中东部、东北中西部地区降水为负距平，低值中心位于山东半岛以西，华南地区、东北东南地区、新疆中部、帕米尔高原等地降水偏多，其中新疆中部地区及华南局部地区的正距平中心距平百分率超过100%。预测图(图 2f)中对华南地区、河套及以西地区、青藏高原西北部的正降水距平，及东北北部、华北东北部、长江上游地区的负降水距平有较好体现。但预测结果中在新疆南部青海北部有一个不真实的低值中心，东北东南部的降水正距平也没有预测出来。

2003年夏季(图 2c)，长江流域和黄河流域之间降水显著偏多，高值中心位于淮河流域。西部地区北部及西部、东北北部降水亦为正距平。其余大部降水偏少。预测结果(图 2g)显示江淮流域降水偏少，与实况反位相。除云贵地区、西北地区西北部、华北地区西北部等地的负距平预测准确外，其余大部分地区的预测结果均不理想。

2004年夏季(图 2d)，黄淮流域及西北地区西部降水为正距平，华南大部、东北地区、西北地区中部降水偏少。预测图(图 2h)中除东北地区及西北局部地区的降水负距平、内蒙古中部正距平得到较好体现外，其他地区的预测结果亦不理想。总体来看，2001与2002年的预测结果优于2003与2004年。

为更直观地评估预测结果，把全国划分为6个区域：西北、西南、东北、华北、江淮、华南, 表 1给出了全国范围6个区域每年及4年平均的技巧评分(SS)、距平相关系数(ACC)、异常气候评分(TS)。全国范围4年平均ACC及TS均远大于气候中心平均水平，SS与气候中心平均水平也较为接近，说明本文采用的方法总体上对夏季降水有较好的预测效果。

考察不同年份的预测结果，全国范围的ACC及TS均显示2001和2002年的值大于2003和2004年。其中2003和2004年分别有4和3个区域的ACC低于气候中心平均水平，而2001和2002年分别为1和2个。类似地，2001和2002年分别有2和0个区域的TS低于气候中心平均水平，而2003和2004年分别达到2和3个。2004年全国范围的SS出现了负值(-4.9)，是4年中最低的。该年所有6个区域的SS均小于或等于零，预测结果较差。预测评分显示，2001和2002年的预测结果显著优于2003和2004年，这与从预测图中得到的结论一致。

考察不同区域的预测结果，东北地区的SS及ACC在6个区域中均为最高，4年的ACC均好于气候中心的平均水平；TS相对较低，但与国家气候中心平均水平接近，说明采用的预测方法对东北地区有较好的预测结果，这从预测图中也可以直观看出。西南地区的SS、ACC和TS也均好于国家气候中心平均水平；4年的TS均高于气候中心平均水平，除2004年外，SS评分也较高。华南地区平均及逐年的各项评分均较低，有6个年次低于气候中心的平均水平。华北地区分别有2和3年的SS和ACC低于气候中心平均水平。总体而言，东北、西南预测结果优于西北、华北、江淮、华南地区。此外，注意到华北及江淮地区的TS评分较高，说明建立的方法对异常偏多或偏少的夏季降水有较好的预测能力，而该区域正是我国夏季异常降水预测的重点地区。

需要指出的是，由于我们选择的预测因子的不同、预测因子的时段(如我们采用的是当年3月的因子，而气候中心采用的是2月前的因子)也不同，另外，评分的技巧也许存在着一定差异。因此，这里只是气候中心的结果作为不同区间比较的一个参考的标准。准确的比较需要在相同的前提下进行。同时，我们也注意到2001和2002年长江流域与黄河流域之间(江淮)降水偏少、东南沿海地区降水偏多，而2003和2004年情况与2001和2002年相反，即当全国的降水空间分布呈现出长江流域与黄河流域之间降水偏少(偏多)、东南沿海地区降水偏多(偏少)的分布时，建立的方法预测水平较高(较低)。这一方面可能和季风的强弱有关，而本文建立的方法目前没有引入直接反映季风的因子。另一方面，已有的研究表明^[19-21]，发展阶段的ENSO事件易引起江淮流域降水偏多，而黄河流域、华北地区和江南地区降水偏少。考察2003和2004年的降水和ENSO指数，可以发现这两年的ENSO指数值显著高于2001和2002年，因此，本文建立的方法需要在如何选取El Nino年发展阶段指数作为因子、如何引入反映季风因子等方面进一步深入研究。

4 小结

本文尝试把奇异谱分析-最大熵方法与最优子集回归方法结合起来，建立了一种新的方法。并在综合考虑青藏高原地区的积雪和冻土因子、ENSO、AO、NAO为因子的基础上，应用于中国夏季降水的预报试验，并从回报拟合和试报的结果进行了简单分析，结果显示出，本文提出的预测方法对于夏季降水的气候预测是可行的。回报结果显示出，就全国尺度而言，回报出的1961—2000年夏季降水与实际降水量有较高的距平相关系数，160站均通过了0.01的显著性水平检验。其中，青藏高原地区、新疆中部、四川重庆等地、内蒙古中部、黑龙江中部吉林东部、江苏沿海地区、浙江北部安徽中西部及广西贵州中西部等地区的相关系数达到了0.80(超过0.01的显著性水平检验)。

对2001—2004年降水量进行试报，结果表明，全国160站4年的预报准确率平均值为69%，略高于目前国内气候预报的平均水平。通过对2001—2004年逐年进行试报，结果表明，处于El Nino发展阶段年的全国范围总体预测结果更为理想。分区域检验结果表明，东北、西南地区预测结果较其他地区更为理想，华北及江淮地区异常降水预测的能力较强。由于本文使用了有限的预测因子，致使江淮流域与华南地区夏季降水的预测与实况相反，因此本方法还需使用更多因子去进一步验证和完善。