2000年前后,我国各级气象部门陆续建立了自动气象站,自动气象站测量气压广泛使用芬兰VAISALA公司生产的PTB220数字气压表。该数字气压表的校准不确定度已达到0.15 hPa,远远高于人工观测气压使用的动槽或定槽水银气压表[1-2]。为适应这一变化,2008年国家气象计量站引进了美国DHI公司的PG7607全自动气体活塞压力计(以下简称PG7607),最佳测量能力由原来的35 ppm (1 ppm=10-6)提升到了8 ppm。尽管活塞压力计在最佳测量能力上优于其他压力测量仪器,但其所复现的大气压力量值的不确定度与活塞的零级有效面积、所加载的砝码组的质量、当地重力加速度等十几项因素密切相关。在这十几项影响因素中,零级有效面积所引入的相对不确定度分量与活塞压力计复现压力的相对不确定度之间的相关性达到100%,是影响最为严重的因素之一。因此,准确的确定零级活塞有效面积的数值,是保证PG7607所复现的压力量值准确可靠的前提。
对于零级有效面积的确定,从实验的简单性和成本的经济性出发,国内普遍采用被称为压力平衡法的实验过程来完成。近年来,国际上越来越多的报告表明,通过基于几何测量的几何法,正逐步成为确定零级有效面积的另外一条途径。
基于这样一个背景,国家气象计量站分别采用压力平衡法和几何法获取了PG7607零级有效面积,在对两个结果进行了分析和比较后,依据结果不确定度最小原则,最终选择了几何法所获得的结果作为零级有效面积的值。
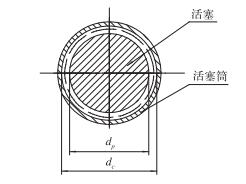
1 零级活塞有效面积零级活塞有效面积(以下简称活塞有效面积)是指在某一温度、零压力下活塞系统的等效面积。活塞有效面积的温度一般是在20℃或23℃条件下,活塞有效面积[3]在数值上等于活塞截面积与活塞系统间隙面积之半的和,活塞有效面积示意图如图 1所示。图 1虚线圆所表示的面积为活塞有效面积,根据式(1) 计算活塞的有效面积。
|
图 1 活塞有效面积示意图 Fig. 1 Diagram of piston effective area |
| ${A_0} = \frac{1}{4}\pi d_p^2 + \frac{1}{8}\pi (d_c^2 - d_p^2)$ | (1) |
式中:dp:活塞外径,单位为mm;dc:活塞筒内径,单位为mm;A0:活塞组件在零压力和20℃条件下的有效面积,单位mm2。
2 通过几何法计算活塞有效面积 2.1 几何法原理几何法是根据活塞有效面积的定义,对活塞和活塞筒几何尺寸进行测量,根据测量结果计算活塞有效面积。
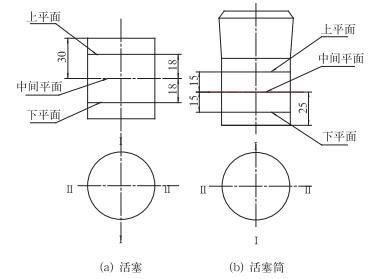
2.2 几何测量及测量结果在2008年初,加拿大国家实验室对PG7607的活塞和活塞筒进行了几何尺寸测量。该实验室分别对PG7607活塞和活塞筒的三个不同高度(中间平面位置、上平面位置和下平面位置)、两个相互垂直的位置(Ⅰ和Ⅱ)进行了测量。在加拿大国家实验室提供的校准报告[4](LS-2008-0001) 中,给出了活塞和活塞筒几何尺寸的测量结果及不确定度。活塞测量的中心高度为距活塞顶向下30 mm的位置,该测量位置为中间平面,距活塞测量中心高度+18 mm的测量平面为上平面,距活塞测量中心高度-18 mm的测量平面为下平面。活塞筒测量的中心高度为距活塞筒底面向上25 mm的位置,该测量位置为中间平面,距活塞筒测量中心高度+15 mm的测量平面为上平面,距活塞筒测量中心高度-15 mm的测量平面为下平面。活塞和活塞筒几何尺寸测量位置如图 2所示。
|
图 2 活塞-活塞筒几何尺寸测量位置 Fig. 2 Dimensional measurement positions for piston and cylinder |
活塞直径测量结果见表 1。
|
|
表 1 活塞S/N 850直径测量结果 Table 1 Diameter measurement results of piston S/N 850 |
活塞筒直径测量结果见表 2。
|
|
表 2 活塞筒S/N 850直径测量结果 Table 2 Diameter measurement results of cylinder S/N 850 |
根据表 1和表 2活塞-活塞筒几何尺寸的测量结果用式(1) 计算活塞有效面积。国外同行在用该公式计算时,未考虑测量平面的权重,只是简单计算活塞、活塞筒测量直径的平均值后,再根据式(1) 计算活塞的有效面积。本文在计算活塞有效面积时,对活塞-活塞筒直径测量结果考虑了权重,根据各截面的权,分别计算活塞和活塞筒的加权直径。
2.3.1 活塞加权直径的计算根据表 1活塞直径测量结果及不确定度,对6个测量结果用加权算术平均值的方法计算活塞的直径。
(a)计算三个测量平面活塞的平均直径
上平面活塞平均直径
(b)计算三个测量平面活塞平均直径标准偏差
首先依据式(2) 分别计算三个测量平面活塞直径的标准偏差,再依据式(3) 计算三个测量平面活塞平均直径标准偏差。
| ${s_{pi}} = \sqrt {\frac{{{{\left( {{d_{pi}} - \overline {{d_{pi}}} } \right)}^2}}}{{n - 1}}} $ | (2) |
式(2) 中:spi:活塞直径测量的标准偏差;dpi:活塞直径;
依据式(3) 分别计算三个测量平面活塞平均直径的标准偏差。
| $\overline {{s_{pi}}} = \frac{{{s_{pi}}}}{{\sqrt 2 }}$ | (3) |
式(3) 中:
活塞平均直径标准偏差计算结果分别为:上平面活塞平均直径的标准偏差
(c)计算三个测量平面活塞平均直径的权
依据式(4)[5]分别计算三个测量平面活塞平均直径的权。
| ${p_{p1}}:{p_{p2}}:{p_{p3}} = \frac{1}{{{{\overline {{s_{p1}}} }^2}}}:\frac{1}{{{{\overline {{s_{p2}}} }^2}}}:\frac{1}{{{{\overline {{s_{p3}}} }^2}}}$ | (4) |
活塞平均直径权的计算结果分别为:上平面活塞平均直径的权pp1为4;中间平面活塞平均直径的权pp2为4;下平面活塞平均直径的权pp3为9。
(d)计算三个测量平面活塞加权的直径
根据式(5) 计算活塞三个测量平面的加权直径dp。
| ${d_p} = \frac{{{d_{p1}}{p_{p1}} + {d_{p2}}{p_{p2}} + {d_{p3}}{p_{p3}}}}{{{p_{p1}} + {p_{p2}} + {p_{p3}}}}$ | (5) |
活塞的加权直径dp为49.968180 mm。
2.3.2 活塞筒加权直径的计算根据表 2活塞筒直径测量结果及不确定度,对6个测量结果用加权算术平均值的方法计算活塞筒的直径。活塞筒加权直径的计算方法与活塞加权直径的计算方法相同,活塞筒的加权直径dc为49.968968 mm。
2.3.3 活塞有效面积的计算将活塞加权直径dp和活塞筒加权直径dc的计算结果分别代入式(1),根据对活塞有效面积有效位的精度分析,π取值为3.141592,活塞有效面积的计算结果为1961.0276 mm2。
2.3.4 活塞有效面积不确定度的计算对式(1) 进行整理,导出活塞有效面积A0为:
| ${A_0} = \frac{1}{8}\pi (d_p^2 + d_c^2)$ | (6) |
由于各分量互不相关,因而合成方差u2(A0)按式(7)[6]计算。
| ${u^2}({A_0}) = {\left[ {\frac{{\partial {A_0}}}{{\partial {d_p}}}} \right]^2}{u^2}({d_p}) + {\left[ {\frac{{\partial {A_0}}}{{\partial {d_c}}}} \right]^2}{u^2}({d_c})$ | (7) |
据表 1及表 2,将u(dp)为0.000075 mm,u(dc)为0.000075 mm,代入式(7),有u(A0)为0.0042 mm。
活塞有效面积的相对不确定度按式(8) 计算。
| ${u_r}({A_0}) = \frac{{u({A_0})}}{{{A_0}}}$ | (8) |
活塞有效面积的扩展不确定度ur(A0)=4.3 ppm(k=2)。
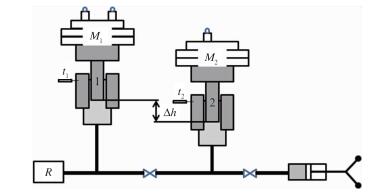
3 通过压力平衡法获取活塞有效面积 3.1 压力平衡法的原理所谓压力平衡法是将使用参考压力测量仪器与PG7607同时测量同一压力,通过调整PG7607上所加载的砝码组的质量,使其与被测压力达到平衡。如图 3所示。平衡后,可根据式(9) 计算PG7607的有效面积。
|
图 3 活塞压力计比对装置 1:计量院活塞;2:计量站PG7607活塞 Fig. 3 Comparison devices of piston pressure gauge |
| ${A_0} = \frac{{Mg\left( {1 - \frac{{{\rho _a}}}{{{\rho _m}}}} \right){\rm{cos}}\theta + {F_r}}}{{({P_s} - \rho gh)\left[ {1 + ({\alpha _p} + {\alpha _c})\left( {t - 20} \right)} \right](1 + \lambda {P_s})}}$ | (9) |
式中:M:砝码及活塞质量;gl:重力加速度;ρa:空气密度;ρm:砝码、承重盘及活塞平均密度;h:气柱高度;ρf:介质密度;t:活塞温度;λ:弹性形变系数;αp+αc:热膨胀系数,θ:活塞轴线与重力方向的夹角;Fr:活塞和活塞筒之间的摩擦力,表现为活塞的灵敏阈。
3.2 比对及比对数据国家气象计量站的PG7607在2009年4月15日和4月16日与中国计量院的气压基准在国家气象计量站大气压力实验室进行了比对,比对模式为表压模式,比对介质为氮气,比对的压力点为300、500、800、1000、1300和1600 hPa。比对数据及结果见表 3。
|
|
表 3 活塞压力计比对数据及结果 Table 3 Comparative data and results of piston pressure gauge |
将表 3中各压力点活塞面积取平均,作为压力平衡法获得活塞有效面积的结果,活塞有效面积的结果为1961.0454 mm2。
3.4 活塞有效面积不确定度的计算根据式(9) 活塞有效面积的计算公式,可知,活塞有效面积是压力、砝码质量、空气密度、砝码密度、重力加速度等量的函数,因此,活塞有效面积不确定度依据式(10) 计算。
| ${u_{rc}}({A_0}) = \sqrt {u_r^2({A_0}) + u_r^2({p_s}) + u_r^2\left( M \right) + {\alpha ^2}{u^2}\left( t \right) + p_s^2{u^2}\left( \lambda \right) + {{\left( {\frac{{\rho g}}{{{p_s}}}} \right)}^2}{u^2}\left( h \right) + {\rm{ta}}{{\rm{n}}^2}\theta {\rm{ }}{u^2}\left( \theta \right) + {{\left( {\frac{1}{{{A_0}{p_s}}}} \right)}^2}{u^2}\left( {Fr} \right)} $ | (10) |
活塞有效面积扩展不确定度计算结果为15 ppm[7](k=2)。
4 两种方法的比较由第2节的计算结果和第3节的实验结果可以看出,通过两种方法所获得的有效面积的差值为9.1 ppm,处于两个结果扩展不确定度的平方和开方所确定的数值区间内。因此,可以认为通过两种方法所获取的有效面积的数值在其各自的不确定度水平上均真实可靠。
同时可以看出,采用几何法所获得的有效面积的扩展不确定度明显优于通过压力平衡法所获得的有效面积的扩展不确定度,仅为后者的30%左右。其原因在于采用压力平衡法来确定有效面积时,所获取的结果受到活塞压力计上所加载的砝码组的质量、实验中的环境温度、活塞上加载压力所形成的活塞的形变、活塞和活塞筒的垂直状态、实验中活塞压力计输出压力基准面与参考活塞压力计输出压力参考面的高度差以及参考活塞压力计测量值等诸多因素的影响,从而降低了实验结果的可靠性,增大了结果的不确定度。而采用基于基本定义的几何法来确定有效面积,除了直径测量的不确定度及活塞和活塞筒的圆度外,几乎不受其他因素的影响,从而使得结果更加准确可靠,具有更小的不确定度。因此,采用通过几何法获取的有效面积作为最终结果,相对于通过压力平衡法所获得的实验结果,更为准确可靠。
5 结论(1) 用几何法计算PG7607活塞有效面积的结果为1961.0276 mm2,该活塞有效面积扩展不确定度的计算结果为4.3 ppm(k=2)。
(2) 用压力平衡法获得PG7607活塞有效面积的结果为1961.0279 mm2,该活塞有效面积扩展不确定度的计算结果为15 ppm(k=2)。
(3) 用几何法获取活塞有效面积的不确定度最小,活塞有效面积为1961.0276 mm2。
| [1] |
PTB220 Series Digital Barometers User's GUIDE[M]. Finland: Vaisala Oyj, 2001:71-72.
|
| [2] |
鞠晓慧, 任芝花, 曹丽娟, 等. 自动与人工观测气压的差异与原因分析[J]. 气象, 2010, 36(1): 104-110. DOI:10.7519/j.issn.1000-0526.2010.01.016 |
| [3] |
蒋思敬, 姚士春. 压力计量[M]. 北京: 中国计量出版社, 1991: 124-135.
|
| [4] |
Callbration report No.LS-2008-0001[R]. 2008 National Research Council Canada.
|
| [5] |
费业泰. 误差理论与数据处理[M]. 北京: 机械工业出版社, 1994: 22-24.
|
| [6] |
李慎安, 施昌彦, 刘风. JJF1059-1999测量不确定度评定与表示[M]. 北京: 中国计量出版社, 1991: 18-20.
|
| [7] |
校准报告, RGpc2009-0018[R]. 北京: 中国计量科学研究院.
|
 2011, Vol. 37
2011, Vol. 37 