2. 河北省气候中心,石家庄 050021;
3. 曹妃甸工业区气象局,唐山 063210
2. Hebei Climate Center, Shijiazhuang 050021;
3. Meteorological Office of Caofeidian Industrial Zone, Tangshan 063210
曹妃甸是唐山市一个距海边18 km的海岛,区位优势和地理位置非常重要,是重要的工业基地。按照曹妃甸工业区发展规划,曹妃甸工业区将利用天然港址优势,建立矿石、原油、煤炭码头以及钢铁生产基地、原油储备基地和大型火力发电厂,以大码头、大钢铁、大化工、大电能等“四大”主导产业为核心,组成相关工业布局。曹妃甸位于唐山沿海,天气气候复杂,灾害性天气频繁,台风、冷空气大风、强雷暴大风等灾害性天气常有发生,威胁着国家和人民生命财产的安全,做好气候灾害的分析与评估非常重要,尤其是大风灾害的评估,对曹妃甸工业区的建设非常重要。
在大风灾害的分析及评估中,需要较为完整的风向、风速时间序列资料,但是,曹妃甸仅有近2年自动气象站的观测资料,不能满足曹妃甸大风灾害评估的需求,必须进行历史大风资料的重建。在短序列气象资料的延长与插补方面,一些专家学者进行过研究与探讨,屠其璞等[1-3]在20世纪70年代末至80年代初对气温、风向等要素的短序列订正与延长从理论和方法上进行了深入的研究;陈坤生[4]、尹文昱等[5]、王传付[6]分别对气温短序列订正方法进行了对比分析,认为回归订正效果较佳,汪婷等[7]对自动站风能数据进行了短序列订正的研究,上述研究中短序列的延长与订正都是对平均值的延长。在资料序列重建方面,荣艳淑等[8]利用华北地区500年旱涝等级资料,采用滑动累计频率法重建了华北地区500年滑动平均降水场序列。
曹妃甸附近气象台站分布较密,地形相对简单,气象要素之间的相关性较好。因此,根据对曹妃甸工业区的建设需求,利用曹妃甸近2年自动气象站的观测资料和周边气象站的历史观测资料,对曹妃甸历史上逐日最大风速、风向资料进行重建与分析。
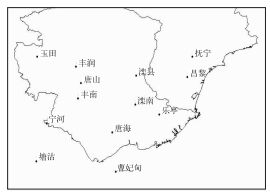
1 资料 1.1 所用资料曹妃甸气象站为无人值守海岛自动站,地处曹妃甸工业区,距唐海、乐亭、滦南较近,分别为35,62和61.6 km,观测场面积为12 m×12 m,场地四周开阔,周边10 m内无高杆植物,100 m内无建筑物,探测环境较好,具有代表性。唐海、乐亭、滦南位于唐山东南部,该区域地势平坦辽阔,台站周围地势开阔,无高大建筑物,探测环境较好,与曹妃甸距离较近、地形差异小,故选唐海、乐亭、滦南作为基本站,曹妃甸及基本站地理位置分布见图 1。所用资料为曹妃甸2007—2008年逐日10分钟最大风速、风向资料和唐海、乐亭、滦南1972—2008年逐日10分钟最大风速、风向资料。
|
图 1 曹妃甸及基本站地理位置分布 Fig. 1 Geographical distribution of Caofeidian and the basic meteorological stations |
自动站观测资料中风向用角度表示,人工观测资料中风向用16个方位表示,为了方便统计并与人工观测一致,将自动站风向参考地面观测规范中的16个方位表示,并规定各风向的风向角(标准见表 1),为了计算方便,16个方位分别用1~16的数字表示,17表示静风。
|
|
表 1 风向与方位的对应关系[9] Table 1 Relationship between wind direction and bearing |
按照上述标准,把曹妃甸2007—2008年的逐日10分钟最大风向用风向角表示,唐海、乐亭、滦南1972—2008年的逐日10分钟最大风向也用风向角表示。
1.3 基本站最大风速资料的均一性检验为了保证资料的可靠性,有必要对唐海、乐亭、滦南这3个基本站的最大风速资料进行均一性检验[10-14],采用SNHT方法进行检验。从邻近站中挑选4个与基本站序列相关系数最高的序列所在的站点,作为参考站。唐海的参考站选为滦南、丰南、塘沽、宁河;乐亭的参考站选为滦南、丰南、唐海、抚宁;滦南的参考站选为玉田、丰润、丰南、抚宁。
用式(1) 建立参考序列ri
| ${r_i} = \left[ {\sum\limits_{j = 1}^4 {\rho _j^2{X_{j,i}}/{{\bar X}_j}} } \right]/\sum\limits_{j = 1}^4 {\rho _j^2} $ | (1) |
式(1) 中ρj是基本站序列与参考站序列Xj, i的相关系数。
用比值法(Yi为基本站序列, Y为其均值)构造检验序列Qi
| ${Q_i} = \frac{{{Y_i}/\bar Y}}{{{r_i}}}$ | (2) |
然后再做标准化处理,得到序列Zi。经检验,用比值法构造的唐海、乐亭、滦南最大风速序列Zi都较好地服从正态分布(检验过程略)。
构造检验统计量T
| $T = \mathop {\max }\limits_{1 \le a \le n - 1} \left\{ {a\bar z_1^2 + \left( {n - a} \right)\bar z_2^2} \right\}$ | (3) |
当T>Tα=0.10时,拒绝被检序列是均一的假设。用该方法对唐海、乐亭、滦南的年最大风速进行检验,结果为:用唐海、乐亭、滦南的1972—2008年的最大风速比值序列求出的统计量T分别为5.87, 6.48, 4.29,当显著水平α=0.10时,Tα=0.10=6.82,均满足T<Tα=0.10[11],即可以认为这3个被检序列是均一的。
2 曹妃甸最大风速、风向资料的重建 2.1 模型的选取风是矢量,在天气气候分析中,经常将矢量风分解为u,v分量。利用该方法,把唐海、乐亭、滦南气象站1972—2008年和曹妃甸2007—2008年最大风资料进行u,v分量分解,建立最大风资料的回归模型,对曹妃甸历史最大风资料进行了重建。
首先利用2007—2008年逐日最大风资料分别计算曹妃甸u,v分量与3个基本站u,v分量之间的相关系数,计算结果见表 2。
|
|
表 2 曹妃甸u,v分量与基本站u,v分量的相关系数 Table 2 The correlation coefficient of u and v components between Caofeidian and basic stations |
分析表明:曹妃甸最大风速的u分量与唐海站u分量的相关系数最大,为0.8619,与乐亭、滦南的相关系数分别为0.6139和0.6905,相关的显著性是显而易见的,这里不作检验。曹妃甸最大风速的u分量与基本站v分量的相关系数都为负值,而且相关性远不如与u分量;曹妃甸最大风速的v分量与基本站u分量的相关系数都很小。
因此,可以认为利用回归模型对曹妃甸最大风速资料重建是合适的,且建立曹妃甸最大风速u分量模型时,仅用基本站最大风速的u分量;建立v分量模型时,仅用基本站最大风速的v分量。
2.2 重建过程按不同月份分别建立回归方程,过程如下:
(1) 将风向角d变换成直角坐标的角度θ=3π/2-d,于是可用公式
| $\begin{array}{l} u = r\cos \theta \\ v = r\sin \theta \end{array}$ | (4) |
式中,u,v分量分别为x,y方向的分量,r为风速。
(2) 假定曹妃甸的最大风速的u分量(或v分量)为y(i),乐亭、滦南、唐海的最大风速的u分量(或v分量)为x1(i),x2(i),x3(i),利用曹妃甸和乐亭、滦南、唐海2007—2008年的逐日10分钟最大风速资料,建立曹妃甸的u分量(或v分量)与乐亭、滦南、唐海的u分量(或v分量)之间的回归方程,回归方程的参数见表 3。经F检验,除了6月份和8月份v分量方程的显著水平分别为0.0001和0.002外,其他方程的显著水平的量级已达到10-6。
|
|
表 3 回归方程及参数 Table 3 The regression equations and their parameters |
分析其原因,可能与河北省不同月份的大风影响系统有关,冬季月份,河北多受强大的地面冷高压控制,大风天气多是由于冷锋过境或高压系统的影响,曹妃甸和相邻测站在相同系统控制下,所以相关性非常好。而夏季各月,由于天气系统比较复杂,有大尺度的天气系统,也有中小尺度的天气系统影响,曹妃甸和相邻测站最大风速不一定全部是相同天气系统的影响,所以相关性较冬季差些。这一点已经通过查阅历史天气图得到了证实。
(3) 将1972—2006年乐亭、滦南、唐海测站的资料代入方程,即可求出1972—2006年曹妃甸的最大风速的u,v分量的估计值。
(4) 利用公式
| $\begin{array}{l} r = \sqrt {{u^2} + {v^2}} \quad {r^2} = {u^2} + {v^2}\\ \theta = \arctan \left| {\frac{v}{u}} \right| \end{array}$ | (5) |
将u,v分量还原为风向和风速。
3 曹妃甸与唐海最大风资料的对比分析 3.1 风向的对比分析 3.1.1 实测资料曹妃甸与唐海站距离最近,因此通过对曹妃甸与唐海的实际观测资料的比较,分析两者之间的关系。
为了客观地表示2个气象站之间的风向关系,用16个方位(最大风速没有出现静风的情况)的风向偏差表示,定义风向偏差D=|T-C|,其中,T为唐海的最大风向方位,C为曹妃甸的最大风向方位,且规定|T-C|=15时D=1, |T-C|=14时D=2。
利用曹妃甸2007—2008年逐日最大风向资料和唐海2007—2008年逐日最大风向资料,统计日最大风向的偏差,表 4为不同季节风向偏差的统计结果及其与风速的关系,可以看出:唐海与曹妃甸两站风向偏差为0(在同一方位)的次数,春季占28.3%,夏季占31.5%,秋季占24.7%,冬季占33.1%;唐海与曹妃甸两站风向偏差≤1个方位(相差≤22.5度角)的次数,冬季和春季分别占71.8%和72.3%,夏季和秋季约分别占63.6%和64.3%;唐海与曹妃甸两站风向的偏差≥2个方位(相差≥45度角)的次数,冬季和春季约占16%,夏季占20.6%,秋季占25.3%。说明冬季和春季唐海站与曹妃甸的风向大部分情况是一致的,而夏、秋季偏差较大的情况比冬春季多一些。
|
|
表 4 2007—2008年唐海与曹妃甸日最大风向的偏差 Table 4 The difference of wind direction between Caofeidian and Tanghai from 2007 to 2008 |
从表 4中还可以看出,两站风速的大小与风向的偏差关系密切,通常当风速较大时,两站的风向差异相对较小,当风速较小时,两站间的差异较大,这种现象在冬、春两季最为明显。
3.1.2 重建资料表 5给出了1972-2006年曹妃甸重建日最大风向与唐海实测日最大风向的偏差。可以看出:曹妃甸与唐海的风向偏差为0(同一个方位)的次数,春季占46%,夏季占29.4%,秋季占42.7%,冬季占54%;偏差在1个方位以内的次数,夏季占78.4%,其他季节约占90%~95%;偏差大于1个方位的次数相对偏少。从表 5还可以看出,风速较小时,两站风向偏差较大,风速较大时,两站风向偏差较小,这一特征与实测资料一致。
|
|
表 5 1972—2006年曹妃甸(重建资料)与唐海最大风向的偏差 Table 5 The difference of maximum wind direction between Caofeidian (rebuilding data) and Tanghai from 1972 to 2006 |
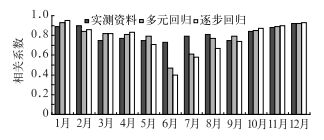
为了考察曹妃甸重建后的最大风速与唐海站实测最大风速相关的稳定性,分别计算了2007-2008年唐海站与曹妃甸实测日最大风速和1972-2006年曹妃甸重建日最大风速与唐海站同期实测最大风速的相关系数,计算结果见图 2,图 2中同时给出了利用逐步回归和多元回归两种方法重建的最大风速与唐海站最大风速的相关系数,相关系数的显著性是显而易见的。
|
图 2 唐海与曹妃甸日最大风速的相关系数 Fig. 2 The correlation coefficient of maximum wind speed between Tanghai and Caofeidian |
分析图 2,可以看出:10,11,12,1,2月份唐海站与曹妃甸观测资料和曹妃甸重建资料的相关系数均在0.84~0.95之间,3,4,5,9月份的相关系数在0.75~0.82之间,即便采用逐步回归技术剔除个别的因子,相关系数也没有太大变化,说明在资料重建过程中,唐海与曹妃甸之间最大风速的相关关系是稳定的。相比之下,夏季两者的相关系数差异较大,其中6月份差异最大,唐海与曹妃甸观测资料之间的相关系数为0.73,与多元回归重建资料的相关系数为0.47,而与逐步回归重建资料的相关系数为0.4(超过了α=0.001的显著水平)。一些试验结果认为[1, 14],利用回归分析进行资料的插补是有实际意义的,本试验结果表明,在因子不多的情况下,多元回归比逐步回归稳定。
分析风向风速的对比分析结果,唐海站与曹妃甸的风向差异在夏秋季偏差较大,风速的相关关系的稳定性也是在夏季差一些,其原因可能是由于不同季节盛行不同的天气系统,冬季受西风带和强大的蒙古高压的影响,天气系统尺度大、强度强,两站在相同系统的影响下,风向偏差不大,风速关系较好;夏季天气系统比较复杂,受中小尺度天气系统影响,风向多变,使得两站的风向产生较大差异,两站风速的相关关系的稳定性相对差一些。
3.3 天气系统检验根据天气学原理,我国常见的大风有冷锋后偏北大风、高压后部偏南大风、低压大风以及台风大风和雷雨、冰雹、飑线和龙卷等强对流风暴引起的大风[15]。唐山东南部地形简单,地势平坦,地理地形条件基本相似,通常情况下,处于相同的环境背景下,特别是当最大风出现时,环境背景更加突出,应该有相应的天气系统与之对应。为了检验1972—2006年曹妃甸重建最大风速与天气系统的对应关系,对每个月的逐日最大风速进行排序,每个月选择10个风速最大的日期,共选择120个样本,针对这120个样本查阅了历史天气图, 进行天气系统检验,检验结果见表 6。50个样本与冷锋配合,37个样本与强大的冷高压配合, 7个样本与气旋配合,19个样本与强对流配合,2次台风影响,5个样本无明显的天气系统配合,均出现在6—9月份, 主要原因是夏季系统比较复杂,这5个大风天气可能由于受中尺度天气系统的影响,在历史天气图上没有反映。
|
|
表 6 曹妃甸最大风速与天气系统的对应关系 Table 6 Relationship between maximum wind speed in Caofeidian and weather systems |
为了搞清曹妃甸周围的唐海、乐亭、滦南的日最大风速的概率分布情况,尝试用不同的概率分布进行了拟合,结果表明,日最大风速用Gamma分布拟合效果最好。Gamma分布密度为[16]:
| $f\left( x \right) = \frac{{{\beta ^\alpha }}}{{\Gamma \left( \alpha \right)}}{x^{\alpha - 1}}{{\rm{e}}^{ - \beta x}}\quad x > 0$ | (6) |
其中
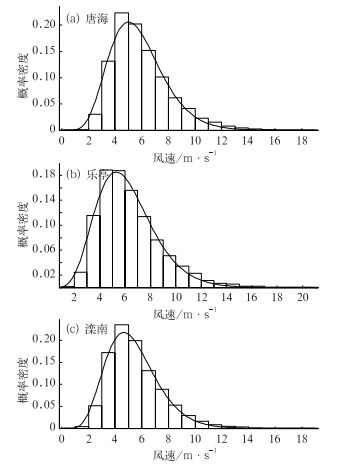
参数α为形态参数,其大小决定Gamma分布的陡峭程度;β为尺度参数,其大小决定Gamma分布的分散度。图 3给出了1972—2008年唐海、乐亭、滦南的日最大风速概率分布密度曲线的拟合情况。
|
图 3 唐海(a)、乐亭(b)、滦南(c)日最大风速的概率分布密度曲线的拟合情况 Fig. 3 Fitting probability density functions of maximum wind speed in Tanghai (a), Laoting (b) and Luannan (c) |
概率分布的检验,定义如下统计量
| ${D_n} = \mathop {Sup}\limits_x \left| {F\left( x \right) - {S_n}\left( x \right)} \right|$ | (7) |
对于连续分布函数F(x),统计量Q(λ)渐近服从柯尔莫哥洛夫分布[1]
| $\mathop {\lim }\limits_{n \to \infty } \left\{ {\sqrt n {D_n} < \lambda } \right\} = Q\left( \lambda \right) = \sum\limits_{k = - \infty }^\infty {{{\left( { - 1} \right)}^k}} {{\rm{e}}^{ - 2{k^2}{\lambda ^2}}}$ | (8) |
如果选取α=0.10,得到Q分布的临界值Qα=1.36,当Q=
|
|
表 7 唐海、乐亭、滦南日最大风速的分布参数和Q值 Table 7 Distribution parameters of maximum wind speed and Q-values in Tanghai, Laoting and Luannan |
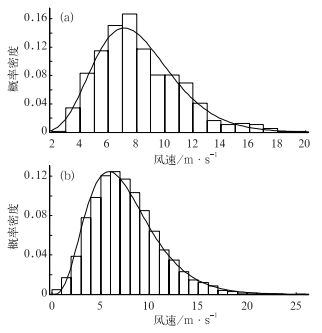
曹妃甸仅有2007—2008两年实测资料,1972-2006年为重建资料,从图 4可以看出曹妃甸实测资料和重建资料的概率分布十分相似,都较好地服从Gamma分布。
|
图 4 曹妃甸日最大风速的概率分布密度曲线的拟合情况(a)实测资料,(b)重建资料 Fig. 4 Fitting probability density functions of maximum wind speed in Caofeidian for (a) observed data, and (b) rebuilding data |
表 8给出2007—2008年和1972—2006年两个不同时段的分布参数的极大似然估计值和Q值。可以看出:
|
|
表 8 曹妃甸、唐海不同时段最大风速的分布参数和Q值 Table 8 Distribution parameters of maximum wind speed and Q-values during 1972—2006 and 2007—2008 in Caofeidian and Tanghai |
(1) 对于分布参数α,所有测站用2007—2008年资料模拟的参数均大于1972—2006年资料模拟的参数;对于分布参数β,其结果恰好相反,用2007—2008年资料模拟的参数均小于1972—2006年资料模拟的参数。
(2) 曹妃甸2007—2008年资料与重建的1972—2006年资料分布参数α的比值为1.36,两个时段β的比值为0.62;唐海站同时段α和β的比值分别为1.41和0.65,说明两个台站分布参数的变化基本一致。
由此可见,曹妃甸重建最大风速的概率分布特征与实测最大风速的概率分布特征相似,与唐海站最大风速的概率分布特征相似,由于曹妃甸地理位置的不同,分布参数存在一些差异,可以认为这种差异是合理的。
5 小结(1) 采用风速的u,v分量分解法建立了曹妃甸最大风资料与唐海、乐亭、滦南最大风资料的回归模型。利用唐海、乐亭、滦南气象站1972—2006年最大风资料,对曹妃甸1972—2006年最大风资料进行了重建。
(2) 对曹妃甸的实测资料和重建资料分别与唐海同时段实测资料进行了对比分析。曹妃甸与唐海的风向存在一些差异,风速较小时,这两站风向偏差较大,风速较大时,两站风向偏差较小。两站实测资料在同一方位的次数,春季占28.3%,夏季占31.5%,秋季占24.7%,冬季占33.1%;曹妃甸重建资料与唐海实测资料的风向在同一方位的次数,春季占46%,夏季占29.4%,秋季占42.7%,冬季占54%。
(3) 分月份选择120个大风个例, 考察与天气系统的对应关系,5个无明显的天气系统配合,其他均有天气系统配合。
(4) 曹妃甸实测资料和重建资料的概率分布十分相似,都较好地服从Gamma分布。
(5) 曹妃甸重建资料具有一定的合理性,该资料序列可以用于大风灾害的分析与评估。
| [1] |
屠其璞, 王俊德, 丁裕国, 等. 气象应用概率统计学[M]. 北京: 气象出版社, 1984.
|
| [2] |
屠其璞. 平均气温序列延长方法的讨论[J]. 南京气象学院学报, 1979, 2: 193-200. |
| [3] |
屠其璞. 气温序列的延长和插补[J]. 气象, 1980, 6(5): 14-15. DOI:10.7519/j.issn.1000-0526.1980.05.006 |
| [4] |
陈坤生. 超短序列月平均气温订正延长方法的比较[J]. 气象, 1982, 8(7): 13-14. DOI:10.7519/j.issn.1000-0526.1982.07.007 |
| [5] |
尹文昱, 祝青林. 大连月平均气温短序列订正方法[J]. 气象科技, 2008, 36(6): 740-744. |
| [6] |
王传付. 中小区域短序列气温资料的延伸[J]. 气象, 1982, 8(3): 25-26. DOI:10.7519/j.issn.1000-0526.1982.03.010 |
| [7] |
汪婷, 吴息, 江志红, 等. 自动站风能参数的短序列订正方法及其应用研究[J]. 应用气象学报, 2008, 19(5): 547-552. DOI:10.11898/1001-7313.20080505 |
| [8] |
荣艳淑, 屠其璞. 华北地区500年滑动平均降水场序列重建[J]. 气象科技, 2004, 32(3): 163-167. |
| [9] |
中国气象局. 地面气象观测规范[M]. 北京: 气象出版社, 2003.
|
| [10] |
李庆祥, 江志红, 黄群, 等. 长江三角洲地区降水资料的均一性检验与订正试验[J]. 应用气象学报, 2008, 19(2): 219-225. DOI:10.11898/1001-7313.20080238 |
| [11] |
刘小宁. 我国40年平均风速的均一性检验[J]. 应用气象学报, 2000, 11(1): 27-33. |
| [12] |
张智, 林莉, 梁培, 等. 宁夏年气温资料的均一性检验研究[J]. 气象, 2009, 35(10): 80-83. |
| [13] |
曾红玲, 张强, 祝昌汉, 等. 三峡库区气压资料的不均一性检验及订正等[J]. 气象, 2010, 36(10): 57-61. DOI:10.7519/j.issn.1000-0526.2010.10.009 |
| [14] |
王海军, 涂诗玉, 陈正洪, 等. 日气温数据缺测的插补方法试验与误差分析[J]. 气象, 2008, 34(7): 83-91. DOI:10.7519/j.issn.1000-0526.2008.07.012 |
| [15] |
寿绍文. 天气学[M]. 北京: 气象出版社, 2009: 483.
|
| [16] |
丁裕国, 江志红. 极端气候研究方法导论[M]. 北京: 气象出版社, 2009: 232.
|
 2011, Vol. 37
2011, Vol. 37 