室外热环境是指作用在建筑外围护结构上的一切热物理量总称,在相同气温下,人们感觉到的舒适程度千差万别[1-2]。随着生活水平的提高,人们开始关注未来天气条件下人体舒适度、人体从事劳动的适宜强度以及注意事项[3-9]。在室外的热环境研究中,湿球黑球温度(TWBG)作为一种纯物理的简单热应力指标,积累了丰富的经验,并且作为美国职业安全与健康的选定指标,在国际上被选入ISO7243标准体系认证,其相比一般的舒适度指标,不仅与干球温度和湿度、风有直接关系,还与太阳辐射有密切的联系,更加准确地体现户外人体的热应力情况[10-12]。同时,作为国际上通行的职业安全健康指标,在长期研究后形成了规范的体系标准,在已知TWBG的基础上,可准确给出适合不同行业(室外活动)劳动者的最佳劳动休息比。在目前的研究中,TWBG被广泛应用于建筑、劳动安全健康、热环境评估等领域,而利用常规气象资料计算TWBG的研究,也已被国内外学者开展,但将其作为预报产品,指导室外劳动安排的研究却显见报道。Andreas Matzarakis等2007年开发的Rayman模型以及平均辐射温度参数化方案[13]为TWBG的预报提供了可能,本文首先通过太阳辐射、大气温度、相对湿度、风、平均辐射温度建立湿球黑球温度简化计算方程,接着通过引入和消化Rayman模型、GB/T 17244-1998和ISO 7243标准体系,建立以云、大气温度、相对湿度、风作为预报因子的TWBG产品预报和服务流程,最终增强和提高我国环境气象服务能力。
1 资料和方法 1.1 资料说明选取天津市边界层观测站内2008年5—10月、2009年5—7月观测资料:包括逐时湿度、风、辐射资料(短波辐射以及短波反射辐射)、每日3次的云量,TWBG资料包括3个部分,干球温度、湿球温度、黑球温度,通过公式(1) 求解湿球黑球温度[9]。
| $ {T_{{\rm{WBG}}}} = 0.7{T_s} + 0.2{T_g} + 0.1{T_a} $ | (1) |
式中Ts为湿球温度,Tg为黑球温度,Ta为干球温度。
1.2 模式和方法介绍 1.2.1 Rayman模型Rayman模型是Andreas Matzarakiskai开发的热环境评估模型,模型以云、风、大气温度、相对湿度、水汽压等为输入因子,通过求解人体热量平衡方程,获取TPE(人体生理等效温度)、PMV(预计冷热感指标)、TSE(标准有效温度)等热环境评价因子。模型中平均辐射温度可以基于云量或太阳辐射观测资料进行计算[14]。
1.2.2 基于太阳辐射计算平均辐射温度平均辐射温度(Tmrt)为发射黑体辐射(ε=1) 的环境表面均一温度,该黑体环境与人体的辐射热交换和真实环境一致,其值取决于环境中长、短波辐射[15]。实际测量可选择来自东、南、西、北和上、下的长、短波辐射计算,本文采用Andreas Matzarakis的参数方案,对其进行求解,具体如下:
当仅有太阳短波总辐射时:
| $ {T_{{\rm{mrt}}}} = {\left[{\frac{1}{\sigma }\sum\limits_{i = 1}^n {({E_i} + {a_k}\frac{{{D_i}}}{{{\varepsilon _p}}}){F_i}} } \right]^{0.25}} $ | (2) |
式中ak为短波吸收系数;σ为Stefan-Boltzman常数,Fi为权重系数。εp为人体发射系数,Di为散射和反射辐射之和,Ei=εiσTsi4。
当有直接太阳辐射照射时:
| $ {T_{{\rm{mrt}}}}^{'} = {\left[{T_{_{{\rm{mrt}}}}^{^4} + {f_p}{a_k}\frac{{{I^*}}}{{{\varepsilon _p}\sigma }}} \right]^{0.25}} $ | (3) |
式中I*垂直于入射方向的太阳辐射强度,fp为表面反射率(是入射方向和身体姿态的函数)。
1.2.3 基于云量计算平均辐射温度缺乏辐射资料时可以用云量计算平均辐射温度,误差约在20%左右,其中太阳高度角(hsl):(4)~(9) 估算:
当hsl≤4°时,
| $ {R_{{\rm{prim}}}} = 1.4{(1.388-0.215{h_{{\rm{sl}}}})^2}(1-0.01{a_c}) $ | (4) |
当hsl>4°, N≤4%时,
| $ {R_{{\rm{prim}}}} = 1.4(-100.428 + 73.981{\rm{ln}}{h_{{\rm{sl}}}})(1-0.01{a_c}) $ | (5) |
当hsl>4°, 20%<N≤50%时,
| $ {R_{{\rm{prim}}}} = 1.4{{\rm{e}}^{(5.383-16.072/{h_{{\rm{sl}}}}}})(1-0.01{a_c}) $ | (6) |
当hsl>4°, 51%<N≤80%时,
| $ {R_{{\rm{prim}}}} = 1.4{{\rm{e}}^{(5.012-11.805/{h_{{\rm{sl}}}}}})(1-0.01{a_c}) $ | (7) |
当hsl>4°, N>80%时,
| $ {R_{{\rm{prim}}}} = 0.9506h_{_{{\rm{sl}}}}^{^{1.039}}(1-0.01{a_c}) $ | (8) |
式中ac为皮肤、服装的反射率,一般取31%,N为云量,Rprim为中间量,计算出Rprim后,可计算平均辐射温度:
| $ {T_{{\rm{mrt}}}}^*= {\left[{\frac{{{R_{{\rm{prim}}}}}}{{5.39 \times {{10}^{-8}}}} + \left( {273 + t} \right)^4} \right]^{0.25}} -273.15 $ | (9) |
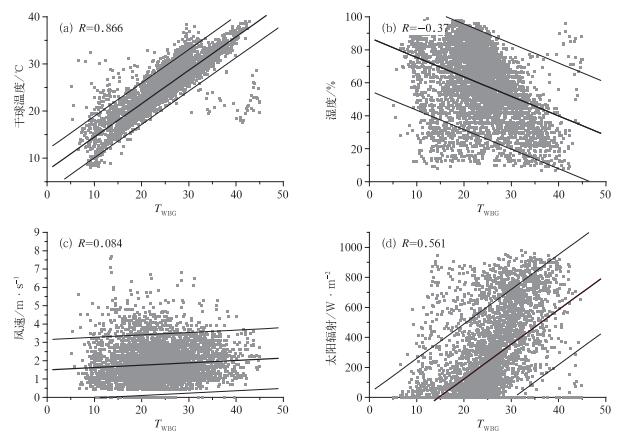
图 1表明干球温度、相对湿度、太阳辐射、风速与TWBG指标的相关关系,其中粗线是回归线,回归线两侧的细线是总体均数90%的可信区间。图 1表明:TWBG与干球温度相关性最好,太阳辐射次之,均呈正相关,相对湿度与TWBG呈负相关,做偏相关分析,排除相对湿度和干球温度之间的关系,相对湿度与TWBG也呈正相关,而风速与TWBG的相关性则较差,呈现弱的正相关性。在了解4个参量与TWBG指标关系的基础上,运用最小二乘法建立4个参量与TWBG的多元回归方程,得式(10):
|
图 1 干球温度(a)、湿球(b)、风速(c)、太阳辐射(d)与TWBG的关系 Fig. 1 The relation of (a) dry bulb temperature, (b) wet bulb temperature, (c) wind speed, and (d) solar radiation with TWBG |
| $ {T_{{\rm{WBG}}}} = 1.0031{T_a} + 0.021RH-0.083V + 0.002SR-2.822 $ | (10) |
式中RH为相对湿度,V为风速,SR为太阳短波辐射。
表 1和表 2给出公式(10) 的统计信息和检验结果,由表显示该方程的决定系数为0.757,F值为4033.755,通过显著性水平检验(P < 0.01),而干球温度、太阳辐射、相对湿度均通过t检验,显示回归方程取得不错的拟合效果。在标准化方程中,显示干球温度是TWBG变化最主要的原因,而风速对TWBG影响较小,风速变化1%时,TWBG仅变化0.013%。
|
|
表 1 基于常规气象要素回归模型的统计信息 Table 1 Regression model of statistical information based on the conventional meteorological elements |
|
|
表 2 基于常规气象要素回归系数及其假设检验 Table 2 Regression coefficient and hypothesis testing based on the conventional meteorological elements |
在建立常规气要素计算TWBG的简化计算方程基础上,引入平均辐射温度(Tmrt)建立回归方程如下:
| $ {T_{{\rm{WBG}}}} = 0.987{T_a} + 0.019RH-0.077V + 0.044{T_{{\rm{mrt}}}}-2.316 $ | (11) |
式中RH为相对湿度,V为风速,Tmrt为平均辐射温度,Ta为干球温度。
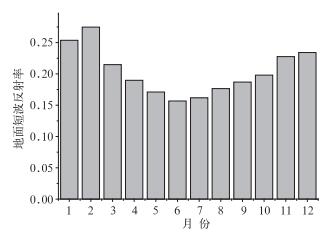
表 3和表 4给出公式(11) 的统计信息和检验结果,由表显示该方程的决定系数为0.756,F值为4026.732,通过显著性水平检验(P < 0.01),回归方程取得不错的拟合效果。公式(11) 中平均辐射温度由Rayman模型[公式(2)、公式(3)]求得,模型的输入参数为太阳短波辐射、大气温度、相对湿度、风速和地面反射率,其中地面反射率(α)根据天津边界层观测站2009年的观测结果,设定α=0.17(如图 2)。
|
|
表 3 基于平均辐射温度回归模型的统计信息 Table 3 Statistical information based on regression model of average radiation temperature |
|
|
表 4 基于平均辐射温度回归系数及其假设检验 Table 4 Regression coefficient and hypothesis testing based on average radiation temperature |
|
图 2 天津地区2009年地面反射率逐月变化 Fig. 2 Monthly variation of ground reflectivity in Tianjin during 2009 |
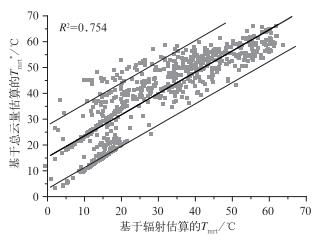
为配合预报因子选择的需要,分别基于总云量和地面太阳短波辐射计算平均辐射温度,由图 3显示,两者的计算结果有较好的一致性(R2=0.754),但整体均值基于总云量估算的Tmrt*偏高,通过线性方程修正(图 3)
|
图 3 基于辐射估算Tmrt与云量估算Tmrt*的相互关系 Fig. 3 The relationship between Tmrt based on radiation and Tmrt* based on cloud estimation |
| $ \begin{array}{l} {T_{{\rm{mrt}}}} = {T_{{\rm{mrt}}}}^*\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(夜间, N \le 5)\\ {T_{{\rm{mrt}}}} = 1.035{T_{{\rm{mrt}}}}^*-13.425\;\;\;\;\;\;(其他) \end{array} $ | (12) |
式中Tmrt*为基于云量观测估算的平均辐射温度,N为总云量,公式(12) 选取2008年观测作为样本建立方程,2009年观测进行检验修正。基于修正方程计算的Tmrt相对误差由45%下降到17.9%,基本满足需要。
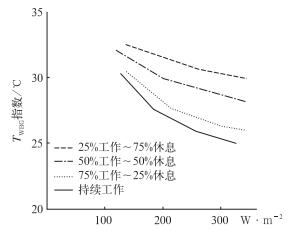
3 讨论通过对TWBG的预测可以指导未来时段不同行业(室外)劳动强度的安排(图 4,图 5),并将2009年7月23日作为预报个例进行说明。
|
图 4 各种劳动/休息时间的TWBG参考曲线 Fig. 4 Reference curves about sorts of labor/rest time TWBG |
|
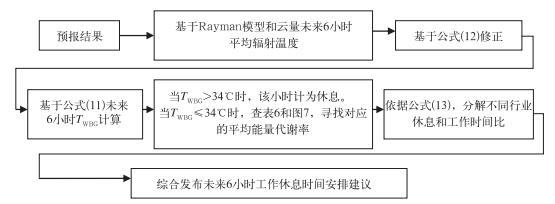
图 5 TWBG产品预报和运用流程 Fig. 5 TWBG product forecast and operation process |
| $ \eta \times 60 = {\eta ^*}t + 32.5\left( {60-t} \right)\\ p = t/\left( {60 - t} \right) $ | (13) |
式中η为该小时TWBG所对应热应力感觉的平均代谢率(表 5),η*为从事行业的平均能量代谢率,t为劳动时间,单位为分钟,p为劳动休息时间比。
|
|
表 5 能量代谢率分级[17] Table 5 The classification of energy metabolization rate |
根据短时预报结果(表 6),表 7给出TWBG预报结果及运用,针对不同用户,可以设定不同的劳动强度和代谢水平,根据公式(13) 以及表 5和图 6进行计算,给出未来6小时室外工作安排建议,合理安排工作时间和工作量,避免高温条件下,室外工作给人体带来的伤害。
|
|
表 6 天津市区2009年7月23日短时预报结果 Table 6 Short-term forecasting results inTianjin on July 23 2009 |
|
|
表 7 2009年7月23日TWBG部分预报结果和建议 Table 7 The forecast results and suggestions for the 23 July 2009 case |
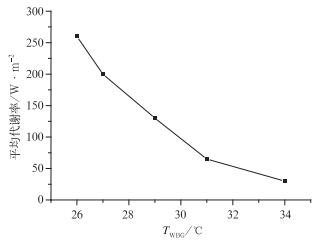
|
图 6 TWBG和平均代谢率关系图TWBG评价指标选择中 Fig. 6 The relation of TWBG and average metabolization rate |
(1) 通过TWBG与温度、相对湿度、太阳辐射、风速、平均辐射温度的相关关系,分别建立基于常规气象要素和基于平均辐射温度的TWBG指标简化计算方法。
(2) 通过Andreas Matzarakis的方案和RayMan模型,将云量因子引入TWBG回归方程中,实现平均辐射温度的简化计算,建立其与气象预报因子匹配的预报方案。
(3) 根据GB/T 17244-1998和ISO 7243标准体系,将TWBG预报产品运用于环境气象预报,给出未来6小时室外工作安排建议,避免高温条件下室外工作给人体带来的伤害。
| [1] |
吴兑. 多种人体舒适度预报公式讨论[J]. 气象科技, 2003, 12(31): 370-372. |
| [2] |
黄海霞, 李建龙, 黄良美. 南京市小气候日变化规律及其对人体舒适度的影响[J]. 生态学杂志, 2008, 27(4): 601-606. |
| [3] |
谈建国, 邵德民, 马雷鸣, 等. 人体热量平衡模型及其在人体舒适度预报中的应用[J]. 南京气象学院学报, 2001, 24(3): 384-390. |
| [4] |
张书余. 城市环境气象预报技术[M]. 北京: 气象出版社, 2006: 119-148.
|
| [5] |
吴结晶, 李瑞光, 穆美舒, 等. 青岛市区夏季暑热指数指数初探[J]. 气象, 2000(4): 33-36. DOI:10.7519/j.issn.1000-0526.2000.04.008 |
| [6] |
陈莉, 李帅, 周永吉, 等. 用标准有效温度和不舒适指标研究哈尔滨热舒适状况[J]. 气象, 2008, 34(1): 73-79. |
| [7] |
杨成芳, 薛德强, 李长军. 山东省人体舒适度区域特征研究[J]. 气象, 2004, 30(10): 7-11. DOI:10.3969/j.issn.1000-0526.2004.10.002 |
| [8] |
李凤云, 杨玉霞. 体感温度预报方法的改进[J]. 气象, 2002, 28(4): 10-11. |
| [9] |
李兴荣, 张小丽, 隋高林, 等. 深圳夏季典型晴天不同小气候区温湿及舒适度特征[J]. 气象, 2010, 36(10): 62-66. DOI:10.7519/j.issn.1000-0526.2010.10.010 |
| [10] |
张磊, 孟庆林, 赵立华, 等. 室外热环境评价指标湿球黑球温度简化计算方法[J]. 重庆建筑大学学报, 2008, 30(5): 108-117. |
| [11] |
钱炜, 唐放鸣. 城市户外环境热舒适度评价模型[J]. 西安建筑科技大学学报, 2001, 33(3): 229-232. |
| [12] |
林波荣. 绿化对室外热环境影响的研究[M]. 北京: 清华大学出版社, 2004: 106-127.
|
| [13] |
Andreas M, Frank R, Helmunt M. Modelling radiation fluxes in simple and complex environments-application of Rayman model[J]. Int J Biometeorol, 2007, 51: 323-334. DOI:10.1007/s00484-006-0061-8 |
| [14] |
Andreas M, Frank R. Application of Rayman for tourism and climate investigations[J]. Annalen der Meteorologie, 2007, 41(2): 631-636. |
| [15] |
余永江. 基于人体与环境热平衡模型的中暑等级预报[D]. 南京: 南京信息工程大学, 2008: 14-16. http://cdmd.cnki.com.cn/Article/CDMD-10300-2008092232.htm
|
| [16] |
国家技术监督局热环境. 根据TWBG指数(湿球黑球温度)对作业人员热负荷的评价GB/T 17244-1998.
|
 2011, Vol. 37
2011, Vol. 37 