2. 北京市气象局,北京 100089;
3. 兰州大学大气科学学院,兰州 730000;
4. 青海省果洛州气象台,果洛 814000
2. Beijing Meteorological Service, Beijing 100089;
3. College of Atmospheric Sciences of Lanzhou University, Lanzhou 730000;
4. Guoluo Meteorological Observatory, Qinghai Province, Guoluo 814000
热带气旋结构是影响其移动和强度变化的一个重要因子[1-6]。因此,进一步认识台风细微结构特征对于其路径和强度预报都有重要意义。20世纪90年代前对于台风结构的研究主要基于Ooyama提出的轴对称动力框架[7],Guinn等[8]在讨论台风雨带结构时指出典型的热带气旋是由轴对称流场及非轴对称流场所组成,台风的一个研究重点是非轴对称动力结构。随着多普勒天气雷达的发展,利用其高时空分辨率及组网优势,使之成为分析台风细微结构的有力工具。Marks等[9]利用机载多普勒雷达与地面雷达对Alicia(1983) 台风做双多普勒雷达分析,对其环流结构有详细的分析,发现在台风低层的2~4 km间有最大的内流,在高层(10 km或以上)则是强外流,在眼墙部分为强的对流尺度的上升及下降运动。Wood等[10]讨论了理想流场兰金模型在单雷达上的旋转和辐合辐散特征。由于天气雷达只能直接得到径向速度,通过不同的反演方法将径向速度还原为真实大气的三维流场结构、分析台风的动力结构特征才变得容易和直观。Lee等[11]提出VTD(Velocity Track Display)技术,该技术基于机载雷达穿越台风中心,假定台风为兰金环流模型,反演出台风的流场结构。Roux等[12]进一步发展了VTD技术,实际上是将VTD技术应用在机载雷达两次穿过台风中心,并且假定两次穿越台风的过程中台风结构不变,即考虑为两部机载雷达同时观测,反演出台风的环流结构。周仲岛, Lee等[13-14]将VTD技术发展为基于地基雷达的GBVTD(Ground Based Velocity Track Display),并通过台风个例指出,该方法能够在较短时间内解析台风环流结构的变化。江晋孝等[15]利用GBVTD技术分析台风纳莉,“纳莉”台风轴对称最强切向风,随高度向外倾斜,且包含非轴对称项之最大切向风亦出现在强回波附近,最强切向半径收缩时,风速亦有增强的情形,登陆后,双雷达合成风场有较强的非轴对称径向风分量,反演结果不能得到较好的风场。张雅茹等[16]将GBVTD方法推广至两部多普勒雷达,可以将台风本身环流与环境场的平均风场分离,提升反演的切向风的准确性。Jou等[17]改进了GBVTD方法提出适用更广的GVTD(Generalized Velocity Track Display)方法,从本质上改善了非轴对称风场的反演结果和反演区域的限制。此外,还有很多学者科研人员利用单多普勒天气雷达或者双多普勒天气雷达不同的反演方法分析台风的结构[18-24]。
综上所述,台风动力结构研究是台风研究中的一个重要方面,一种好的风场反演方法对于台风动力结构的特征分析具有重要意义,相对于传统的基于单雷达的风场反演方法,对于台风这样尺度的系统在反演区域上受到一定的限制,更适用于局地强对流系统的风场反演[25-27]。本文中利用邱崇践等[28]提出的两步变分法反演出“天鹅”台风风场结构并分析其特征。该两步变分法可以应用多部雷达联合反演出整个台风风场结构,突破了一般的双多普勒雷达只能在两部雷达的公共区域反演风场的限制,充分利用组网优势,整个组网区域内都可以作为反演区域,反演结果经个例检验证实其具有一定的可靠性[28-30]。
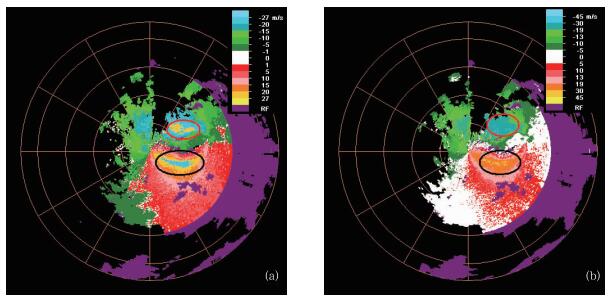
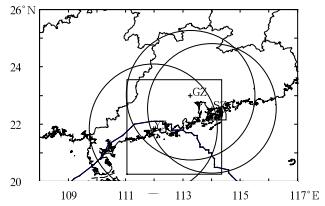
1 反演结果验证 1.1 反演资料及区域2009年第7号台风天鹅于8月3日在南海海面生成, 并于8月4日22时20分(本文统一使用UTC时间)在广东台山沿海登陆。“天鹅”台风登陆后移动变慢,考虑到将整个台风环流作为目标反演区域,选取雷达资料的时次主要考虑整个台风都在布网雷达的有效覆盖范围内,为此,本文选取了四个时次(2009年8月5日00:30、02:30、04:30、06:30) 的广州、深圳和阳江的新一代天气雷达资料,由于几个时次的径向速度在低层仰角均存在不同程度的速度模糊,所以先将径向速度去模糊,本文利用自动二维多途径退模糊方法[31]对基数据径向速度做退模糊处理,图 1为阳江雷达2009年8月5日02:30时刻0.5°仰角上退速度模糊前后的效果图,图中椭圆标注的为有速度模糊区域和对应的退模糊后区域。反演时将径向速度资料格点化水平分辨率为0.01°×0.01°,垂直方向上均匀间隔500 m的格点径向速度。反演格点数为110×110,格距为0.03°,区域111.05°~114.35°E,20.25°~23.55°N,反演层数为30层,均匀间隔500 m。台风天鹅路径、反演区域及组网雷达区域如图 2(其中台风路径资料取自中国天气网)。
|
图 1 2009年8月5日02:30 UTC阳江雷达0.5°仰角退速度模糊前(a)后(b)效果图 Fig. 1 The radial velocity observed by Yangjiang SA radar station on 0.5° elevation at 02:30 UTC 5 August 2009 before (a) and after (b) dealiasing |
|
图 2 “天鹅”台风登陆路径、反演区域及雷达组网区域示意图 Fig. 2 The sketch of typhoon Goni track, retrieved region and radar net coverage |
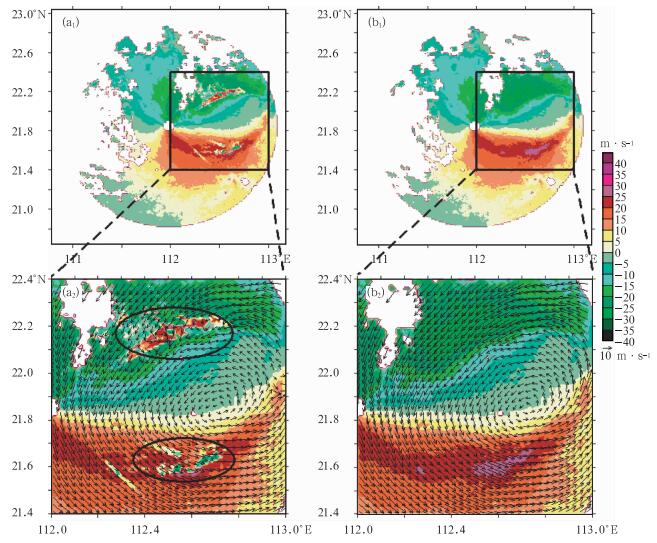
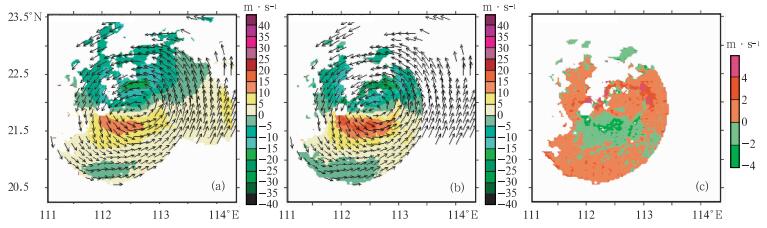
图 3是阳江雷达在02:30时刻退模糊前后反演的结果,很明显存在速度模糊的区域对应的反演结果是错误的,图中椭圆标出的区域,这也充分说明在反演风场前如果存在速度模糊则必须退模糊,而且退模糊效果直接影响风场反演的结果。另外,我们将反演得到的风场反算为雷达站的径向速度并与雷达站对应时刻实测径向速度做比较,如图 4中, 图 4a是反演结果在4 km高度上沿阳江站的径向速度,图 4b是阳江站在4 km高度上的水平径向速度,图 4c是图 4a减去图 4b得到的误差图。对比图 4a与图 4b,零速度线、正负速度区、大速度区等对应得很好,但在大速度区较实测结果偏小,从图 4c中可以看出反演结果与实测结果总体相差不大,平均小于2 m·s-1,极少地方大于3 m·s-1, 对于这样的一个反演结果,还是具有较好的可信度。
|
图 3 2009年8月5日02:30 UTC退速度模糊前(a)后(b)反演结果对比 Fig. 3 Comparison of horizontal wind retrieved by two-step variational method before (a) and after (b) dealiasing at the height of 2 km at 02:30 UTC 5 August 2009 |
|
图 4 2009年8月5日02:30 UTC反演结果与阳江站观测结果对比 (a)风矢量为反演结果,彩色图为反演结果沿阳江站的投影,(b)风矢量为反演结果,彩色图为阳江站的观测结果,(c)表示阳江站的区域由(a)减去(b) Fig. 4 Comparing the retrieval wind after translating to radial velocity and the single-radar observation at the height of 4 km at 02:30 UTC 5 August 2009 (a) vector comes from retrieval and shaded represents the projection of retrieval to Yangjiang, (b) the same as (a) but shaded represents Yangjiang observation, and (c) absolute error: (a) minus (b) |
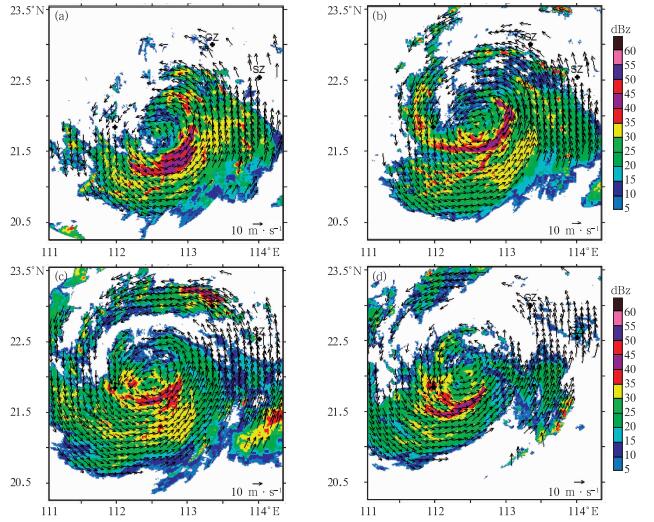
图 5中分别对应2009年8月5日00:30、02:30、04:30、06:30四个时刻在4 km高度上反演的水平风场与回波强度叠加图。四个时刻都较好地反演出“天鹅”台风的环流结构,单从回波强度图看,四个时刻台风眼的无回波或弱回波区都不明显,但都存在较强的环状眼墙。经过反演得到的水平风场都反演出了水平环流中心,从回波强度的连续动画上可以看到“天鹅”的环流中心较好地对应着反演的水平环流中心,另外从图 1中阳江雷达出现速度模糊的位置与图 5b中对应的位置上反演的水平风场可以看出,反演的水平风场方向几乎与雷达站与速度模糊区连线平行,即在雷达径向速度上有较大的分量,从而在该区域出现速度模糊,这也说明该反演结果是合理的。从这四个时刻的回波强度图还可以看出,回波区域经历了由少变多,再由多变少的过程,对应于反演的水平风场在环流中心和环流形状上都有一些变化,但在中心的右侧区域都存在相对于其他区域较为明显的较大风速,这也是“天鹅”风场非对称性的表现。大风速区在00:30与02:30时刻都对应着大片的较强回波区,回波区中镶嵌着一些对流泡,然而在04:30与06:30时刻也都在对应区域存在较大风速,却只对应着小片的较弱回波区,出现这种情况可能是风速的辐合辐散所致,在环状较大风区的前部应该是风速的辐合区,而在其后部应该是风速的辐散区,这样对应着04:30时刻在环状较大风区的前面有新的强回波生成,而对应着06:30时刻在环状较大风区后面回波减少了且变弱。
|
图 5 2009年8月5日各个时刻4 km高度上反演的水平风场与回波强度叠加图(a) 00:30; (b) 02:30, (c) 04:30; (d) 06:30 Fig. 5 Wind vector and reflectivity at the height of 4 km at different time: (a) 00:30, (b) 02:30, (c) 04:30, (d) 06:30 UTC 5 August 2009 |
早在1901年Rankine提出了Rankine涡旋模型[32],后来又有一些研究人员提出类似的涡旋模型。目前很多研究仍然沿用Rankine环流模型, 径向风速分量vr(r)和切向风速分量vt(r)可以分别表示为:
由于Rankine涡旋模型是完全对称模型,而实际台风多为存在一定非对称性的非对称台风,在以台风为中心,不同方位上的切向速度或径向速度随距台风中心的距离变化曲线也就不同,所以这里将各个距离圈上的切向风速或径向风速平均,在平均之前,为排除台风移动速度带来的影响,将四个时刻反演的结果减去“天鹅”的移动速度,各个时刻的移动速度和移动方向根据当前时刻的台风中心位置和下一时刻的台风中心位置估计出来,从而确定四个时刻“天鹅”的移动速度与移动方向如表 1。
|
|
表 1 “天鹅”台风在各时刻的移动方向与移动速度 Table 1 The estimate values of moving direction and velocity of typhoon Goni |
将除去移动速度的反演水平风线性插值到以台风中心为原点分辨率3 km×1°的极坐标形式,再将水平风分解为切向风与径向风(切向风逆时针为正,径向风远离台风中心为正),分别将未分解的水平风、分解后的切向风与径向风在距台风中心等距离的圈上做平均,平均时只对有有效资料的点做平均,另外还计算了不同距离圈上的反演风场的覆盖率,其意义是距离圈上有效的反演结果点数占整个距离圈上点数的百分比,因为极坐标下各个距离圈上的资料方位分辨率不一致,并随着距台风中心距离的增大而减小,我们又将格点资料插值为方位上等距离的3 km,结果与极坐标下算得的资料覆盖率很接近。最后得到的距离廓线如图 6,图 6a~6d依次对应着00:30、02:30、04:30、06:30四个时刻(下同),高度均为4 km,由于“天鹅”台风整个回波面积不大,所以这里只计算距离其中心150 km范围内的反演结果。四个时刻的反演水平风均在一定的距离内具有较高的资料覆盖率,并随着距“天鹅”中心距离增加而减小;平均径向风基本上在零附近,但在06:30时刻,距离台风中心60~80 km之间有一平均径向速度约为-2 m·s-1的径向风,方向为指向环流中心,这表示径向的风速辐合,与图 5d中的强回波带相对应;切向风随着距台风中心的距离增加而增加,并且在50 km左右内增加速度较快,之外增加变得缓慢,即在50 km左右出现切向风速极值,但在150 km内没有出现最大风速,一方面是由于反演资料的覆盖不完全;另一方面可能受到风场的非对称影响,从图 5上可以看到无论是回波强度还是反演出来的水平风场,“天鹅”台风都是非对称的,而且随着距“天鹅”台风中心距离的增加,资料覆盖率下降,这样平均的结果使得大风区占较大的比重,不能较好地代表距中心等距离上的平均结果。另外,利用周仲岛等[33]的方法求取的最大风速半径也在50~60 km之间,综合以上原因,采用最优拟合拟合了出现在50 km左右以内的切向风速,利用Rankine涡旋模型,并将出现在50 km左右的切向速度极值作为Vtmax,拟合得到的λ值见表 2,拟合得到的λ比较接近Rankine模型的1,说明“天鹅”台风在距离其中心50 km左右内4 km高度上的切向风速基本上是按照Rankine模型线性增加,而在此距离之外平均切向风速仍然增加,但增加较为缓慢,与对称的Rankine环流模型相差较大。此外,极大风速在02:30与04:30时刻较大,而在00:30与06:30时刻有所减小,这也与图 5中的回波区相对应,中间两个时刻有所增强,前后两个时刻有所减弱。

|
图 6 2009年8月5日各个时刻风速随距台风中心的距离变化廓线及距离圈上资料覆盖率 (a) 00:30, (b) 02:30, (c) 04:30, (d) 06:30 Fig. 6 The profile of wind and data frequency along with the distance away from Goni centre at different time (a) 00:30, (b) 02:30, (c) 04:30, (d) 06:30 UTC 5 August 2009 |
|
|
表 2 “天鹅”台风4 km高度上各时刻水平环流按照Rankine涡旋模型的拟合系数 Table 2 Fitting coefficients of Goni according to Rankine vortex model at the height of 4 km |
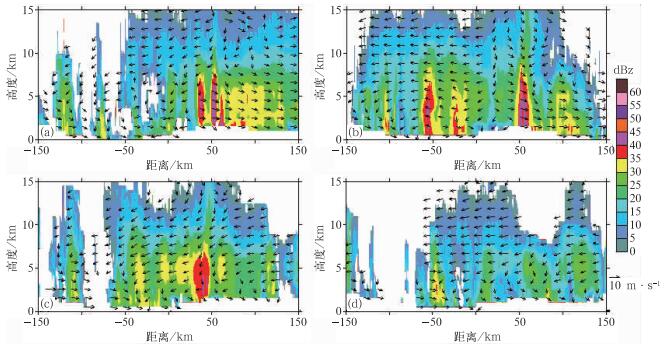
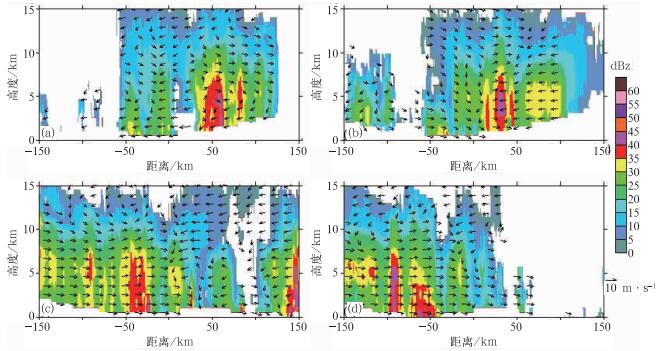
利用两步变分法反演得到的三维风场,分析“天鹅”台风的垂直结构。图 7是去掉移动速度的各个时刻“天鹅”台风中心等距离rc(km)距离圈上沿方位角(正北为零度,顺时针旋转)的垂直剖面,风场为切向速度与垂直速度的合成,四个时刻都以切向风为主,并且强回波区都对应着比较大的风速,较大风速一般都存在7 km左右以下。从图 7中的垂直结构可以发现,“天鹅”台风风场上下层之间的差异,较大风速主要在中下层,并且有3~5个强回波非对称排列,为进一步说明“天鹅”台风的非对称性,如图 8,是图 7中的切向速度在4 km高度上沿方位方向(用弧度表示)的廓线,并对廓线用正弦周期函数最优拟合,从图中可以看出,切向风速廓线存在很多小的波动,平滑掉小波动,四个时刻的切向风速都具有周期为2π的正弦函数变化特征,说明“天鹅”台风的切向风速确实存在波数为1的非对称特征,可认为在图 8中拟合的切向风速最大值方位为“天鹅”台风最大非对称方向,其垂直方向为准对称方向,其垂直结构如图 9、图 10(相对观察者来说,横坐标负值表示台风中心的左边,方位角在180°~360°之间,为正表示在台风中心的右边,方位角在0°~180°之间),风场为径向风与垂直风的合成,图 9与图 10中相应时刻或者各图在各个时刻的风场都存在较为明显的差异。首先看图 9,最大非对称方向上的过台风中心的垂直剖面,00:30时刻,在强回波一侧主要是出流气流,而在另一侧低层为入流气流,中高层是出流气流;02:30时刻在台风中心两侧的都主要为出流气流;04:30时刻台风中心左侧下层为入流,中上层为出流,中心右侧中上层为入流,下层为出流;06:30时刻与04:30时刻高低层出流入流基本一致。再看图 10,准对称方向上过台风中心的垂直剖面,00:30时刻在强回波一侧的低层为入流,中高层为出流,另一侧与之相反;02:30时刻基本与图 9b相应时刻的出流入流情况相反;04:30与02:30的出流入流情况基本一致,主要都是流向台风中心;06:30时刻强回波一侧中下层为入流,上层为出流,另一侧情况与之相反。对比图 9与图 10,最大非对称方向与准对称方向上在同一时刻也存在明显差异,00:30时刻最大非对称方向(图 9a)与准对称方向(图 10a)在低层的入流出流气流相反;02:30时刻最大非对称方向(图 9b)与准对称方向(图 10b)整层的出流入流气流都相反;04:30时刻最大非对称方向(图 9c)与准对称方向(图 10c)在台风中心的左侧中上层与右侧的低层入流出流气流相反;06:30时刻最大非对称方向(图 9d)与准对称方向(图 10d)的入流出流气流只在台风中心左侧的中层相反。综合图 9、图 10的讨论结果,我们可以得到:“天鹅”台风的径向环流不是概念模型中的低层都为入流气流,高层为出流气流,而是在有的方位上是出流,有的方位上是入流,而且不同高度层次其入流出流存在差异,这也正是体现了其非对称性的特点,结合“天鹅”台风的移动路径,最大切向风速位于其移动方向的右前侧,这个结果与一些研究结果一致[2, 22]。

|
图 7 2009年8月5日“天鹅”台风距中心等距离距离rc(km)圈上的垂直结构(a) 00:30, (b) 02:30, (c) 04:30, (d) 06:30 Fig. 7 Vertical structure of Goni at the distance of rc (km) at different time: (a) 00:30, (b) 02:30, (c) 04:30, (d) 06:30 UTC 5 August 2009 |

|
图 8 “天鹅”台风4 km高度上距中心等距离距离rc(km)圈上的切向速度及拟合(a) 00:30、(b) 02:30、(c) 04:30、(d) 06:30 Fig. 8 Tangential velocity and fitting curve of Goni at the height of 4 km at rc(km) different time: (a) 00:30, (b) 02:30, (c) 04:30, (d) 06:30 UTC 5 August 2009 |
|
图 9 2009年8月5日过“天鹅”台风中心沿图 8中拟合最大值方位上的剖面(a) 00:30,(b) 02:30,(c) 04:30,(d) 06:30 Fig. 9 Vertical structure of Goni in the direction of maximum asymmetry of wind at different time: (a) 00:30, (b) 02:30, (c) 04:30, (d) 06:30 UTC 5 August 2009 |
|
图 10 2009年8月5日过“天鹅”台风中心沿图 8中拟合最大值垂直方向上的剖面(a) 00:30,(b) 02:30,(c) 04:30,(d) 06:30 Fig. 10 The same as Fig. 9 but in the direction of quasi-symmetry of wind at different time: (a) 00:30, (b) 02:30, (c) 04:30, (d) 06:30 UTC 5 August 2009 |
本文利用组网天气雷达资料结合两步变分法反演出三维风场分析了2009年第7号台风天鹅四个时刻的结构特征,得到如下结果:
(1) 经过退速度模糊的天气雷达径向速度资料,由两步变分法较好地反演出“天鹅”台风的水平环流结构,并且在其移动路径的右前方存在较大风速区,强回波区也对应存在较大的风速,风速的辐合辐散是其生消的主要原因;
(2) 在4 km高度上,等距离圈上的平均切向风速随距台风中心的距离的增加而增加,并且在最大切向速度圈半径rc内接近Rankine涡旋模型的线性增加,之外增加变得缓慢,平均径向速度随距中心的距离增加变化不明显,维持在零附近;
(3) 拟合“天鹅”台风四个时刻在4 km高度上最大切向风速圈半径rc上的切向速度,得到周期为2π的正弦函数,进一步说明其风场的非对称性,且非对称波数为1;
(4) 最大切向风速圈半径rc垂直剖面上,强回波与切向风速相对应,且较大风速存在于中低层。最大非对称方向与准对称方向的垂直剖面上,入流出流在同一时刻高层、低层或者整层存在差异,即“天鹅”台风的径向环流并不是在低层都是入流气流,而在高层都是出流气流。
两步变分法反演出整个“天鹅”台风的风场结构,并通过反演结果与组网产品格点化的三维反射率因子分析了其结构,其结构既有与经典结构模型相一致的地方也有不相符合的地方,文中将平均切向风速随台风中心距离变化廓线的第一个极值作为最大切向风速值,并将其所在的半径作为最大风速圈半径rc,一方面考虑到资料覆盖率的原因;另一方面也是作为一种假设来做的Rankine涡旋模型拟合。另外,在不考虑反演的结果前提下,文中将格点资料转为以极坐标形式存放时,插值上的处理也必然带来一定的误差。
致谢:本文中使用的两步变分法在调试过程中得到兰州大学研究生段云霞的帮助,在此表示衷心的感谢。
| [1] |
陈联寿. 热带气旋运动研究和业务预报的现状和发展[C]. 台风会议文集. 北京: 气象出版社, 1985: 6-30.
|
| [2] |
陈联寿, 董克勤, 金汉良, 等. 热带气旋全球观[M]. 北京: 气象出版社, 1994: 40-52.
|
| [3] |
雷小途. 热带气旋的结构对其路径偏折的分析[C]. 第11届全国热带气旋科学讨论会论文摘要文集, 中国气象科学研究院, 1999: 58-60.
|
| [4] |
伍荣生. 台风研究中的一些科学问题[J]. 南京大学学报(自然科学), 2007, 43(6): 567-571. |
| [5] |
陈联寿. 热带气象灾害及其研究进展[J]. 气象, 2010, 36(7): 101-110. DOI:10.7519/j.issn.1000-0526.2010.07.017 |
| [6] |
郭鸿基, 林李耀, 陈怡良. 近期台风研究回顾[J]. 大气科学(中国台湾), 2004, 32(3): 205-223. |
| [7] |
Ooyama K. Numerical simulation of the life cycle of tropical cyclones[J]. J Atmos Sci, 1969, 26(1): 3-40. DOI:10.1175/1520-0469(1969)026<0003:NSOTLC>2.0.CO;2 |
| [8] |
Guinn T A., Schubert W H. Hurricane spiral bands[J]. J Atmos Sci, 1993, 50(20): 3380-3403. DOI:10.1175/1520-0469(1993)050<3380:HSB>2.0.CO;2 |
| [9] |
Marks F D Jr, Houze Jr R A. Inner core structure of hurricane Alicia from airborne Doppler radar observation[J]. J Atmos Sci, 1987, 44(9): 1296-1317. DOI:10.1175/1520-0469(1987)044<1296:ICSOHA>2.0.CO;2 |
| [10] |
Wood V T, Lyons S W. Effects of radar proximity on single-Doppler velocity signatures of axisymmetric rotation and divergence[J]. Mea Wea Rev, 1992, 120(12): 2798-2807. DOI:10.1175/1520-0493(1992)120<2798:EORPOS>2.0.CO;2 |
| [11] |
Lee W-C, Marks F D, Carbone R.E.. Velocity track display-A technique to extract real-time tropical cyclone circulations using a single airborne Doppler radar[J]. J Atmos Oceanic Technol, 1994, 11(2): 337-356. DOI:10.1175/1520-0426(1994)011<0337:VTDTTE>2.0.CO;2 |
| [12] |
Roux F, Viltard N. Extended velocity track display(EVTD): An improved processing method for Doppler radar observations of tropical cyclones[J]. J Atmos Oceanic Technol, 1996, 13(4): 875-899. DOI:10.1175/1520-0426(1996)013<0875:EVTDAI>2.0.CO;2 |
| [13] |
周仲岛, 张保亮, 李文兆. 多普勒雷达在台风环流中尺度结构分析的应用[J]. 大气科学(中国台湾), 1994, 22(2): 163-187. |
| [14] |
Lee W-C, Jou B J-D, Chang P-L, et al. Tropical cyclone kinematic structure retrieved from single-Doppler radar observations. Part Ⅰ: Interpretation of Doppler velocity patterns and the GBVTD technique[J]. Mon Wea Rev, 1999, 127(10): 2419-2439. DOI:10.1175/1520-0493(1999)127<2419:TCKSRF>2.0.CO;2 |
| [15] |
江晋孝, 陈台琦. 利用多普勒雷达分析台风风场结构--2001纳莉台风[J]. 大气科学(中国台湾), 2006, 34(3): 177-200. |
| [16] |
张雅茹, 陈台琦, 廖宇庆. 使用EGBVTD分析台风环流非对称结构[J]. 大气科学(中国台湾), 2006, 34(3): 227-240. |
| [17] |
Jou B J-D, Lee W-C, Liu S-P, et al. Generalized VTD retrieval of atmospheric vortex kinematic structure. Part Ⅰ: Formulation and error analysis[J]. Mon Wea Rev, 2008, 136(3): 995-1012. DOI:10.1175/2007MWR2116.1 |
| [18] |
曾吉晖, 陈台琦. 贺伯台风登陆期间结构之双多普勒雷达分析[J]. 大气科学(中国台湾), 1999, 27(4): 295-318. |
| [19] |
周仲岛, 高书正, 李文兆. 纳莉台风登陆后内核中低层环流结构变化特征[J]. 大气科学(中国台湾), 2008, 36(3): 163-178. |
| [20] |
蔡雅婷, 陈台琦. 纳莉台风登陆时的结构演变之多普勒雷达资料分析[J]. 大气科学(中国台湾), 2007, 35(5): 167-187. |
| [21] |
薛根元, 赵放, 冀春晓, 等. 多普勒天气雷达探测揭示的台风云娜(Rananim)登陆前后特征演变研究[J]. 第四纪研究, 2006, 26(3): 370-383. |
| [22] |
赵坤, 周仲岛, 胡东明, 等. 派比安台风(0606) 登陆期间雨带中尺度结构的双多普勒雷达分析[J]. 南京大学学报(自然科学版), 2007, 43(6): 606-620. |
| [23] |
魏应植, 汤达章, 许健民, 等. 多普勒雷达探测"艾利"台风风场不对称结构[J]. 应用气象学报, 2007, 18(3): 285-294. |
| [24] |
刘淑媛, 闫丽凤, 孙健. 登陆台风的多普勒雷达资料质量控制和水平风场反演[J]. 热带气象学报, 2008, 24(2): 105-110. |
| [25] |
周海光, 张沛源. 多种单多普勒雷达风场反演方法对比试验[J]. 气象, 2004, 30(5): 13-16. |
| [26] |
牟容, 刘黎平, 许小永, 等. 四维变分同化方法反演低层风能力研究[J]. 气象, 2007, 33(1): 11-18. DOI:10.7519/j.issn.1000-0526.2007.01.002 |
| [27] |
牟容, 余君, 刘德. 重庆2008年7月21日强对流天气成因及其特征[J]. 气象, 2009, 35(5): 49-56. DOI:10.7519/j.issn.1000-0526.2009.05.007 |
| [28] |
Qiu C-J, Shao A-M, Xu Q. A two-step variational method for three-dimendional wind retrieval from single Doppler radar[J]. Meteorology and Atmospheric Physics, 2006, 91: 1-8. DOI:10.1007/s00703-004-0093-8 |
| [29] |
杨毅, 邱崇践. 利用多普勒雷达资料分析一次强降水的中尺度流场[J]. 高原气象, 2006, 25(5): 925-931. |
| [30] |
段云霞, 邵爱梅, 杨毅. 利用多普勒雷达资料对一次台风流场结构的分析研究[J]. 高原气象(待刊), 2009. |
| [31] |
Zhang J, Wang S. An automated 2D multipass doppler radar velocity dealiasing scheme[J]. J Atmos Oceanic Technol, 2006, 23(9): 1239-1248. DOI:10.1175/JTECH1910.1 |
| [32] |
Rankine W J M. Motions of fluids[M]. A manual of applied Mechanics, 16th ed. Charles Griff and Company, 1901: 574-578.
|
| [33] |
周仲岛, 邓秀明, 张保亮. 多普勒雷达在台风中心定位于最大风速半径决定的应用[J]. 大气科学(中国台湾), 1996, 24(1): 1-24. |
 2011, Vol. 37
2011, Vol. 37 