在许多国家计量院和重要的实验室,已普遍使用活塞压力计作为压力标准器。我国气象部门早在1993年,从美国引进Ruska2465活塞压力计,最佳测量能力达到35 ppm(1 ppm=1×10-6)。基于该活塞压力计所建立的气压量传体系对于保证以动槽或定槽水银气压表为主的气压观测网络观测数据的准确提供了可靠的支撑。
2000年前后,我国各级气象部门陆续建立了自动气象站,自动气象站测量气压广泛使用芬兰VAISALA公司生产的PTB220数字气压表。该数字气压表的校准不确定度已达到0.15 hPa,远远高于人工观测气压使用的动槽或定槽水银气压表[1-2]。为适应这一变化,2008年国家气象计量站引进了美国DHI公司的PG7607活塞压力计,最佳测量能力达到8 ppm。尽管活塞压力计在最佳测量能力上优于其他压力测量仪器,但是其在使用中所复现压力的不确定度受到空气密度、本地重力加速度、环境温度、水平状态、活塞倾斜程度等多达十余项因素的影响。
由于在绝压测量模式下,活塞压力计的输出压力以真空为参考,因此空气密度仅对活塞压力计的表压测量模式存在影响。对于这种影响,国内同行针对密度为1.29 kg·m-3的标准大气状态进行了广泛的探讨和分析。这种方法对于50 ppm以下的活塞压力计已经可以满足应用需要,但是对于不确定度达到8 ppm的基准级活塞压力计来讲尚且不足。本文针对实验室环境条件,对环境空气密度及其不确定度对活塞压力计压力复现结果的影响进行了全量程范围的分析,确定了活塞压力计使用中的最佳大气状态。
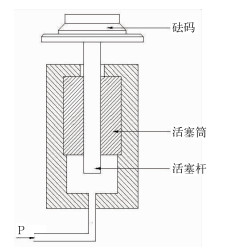
1 活塞压力计工作原理活塞压力计主要由活塞组件和砝码等组成,结构原理如图 1所示。
|
图 1 活塞压力计结构原理 Fig. 1 The structural principle of piston pressure gauge |
当活塞压力计处于平衡悬浮状态时,所复现的压力(实际为压强)满足式(1)。
| $ p = \frac{{mg}}{A} $ | (1) |
式中:p为工作压力(表压),单位:Pa;m为砝码、活塞及连接件总质量(真空中的质量),单位:kg;g为活塞压力计工作地点的重力加速度,单位:m·s-2;A为活塞有效面积,单位:m2。
在表压状态下,活塞压力计在实际使用中,砝码和活塞杆所产生的重力将由于空气浮力的影响而小于理论值,而活塞杆的面积也将在温度和压力的影响下有所变化,因此需要加以修正。实际工作中活塞压力计所复现的压力满足式(2)。
| $ p = \frac{{mg(1 - \frac{\rho }{{{\rho _m}}})}}{{{A_0}\left[{1 + \alpha \left( {t-20} \right)} \right]\left( {1 + \lambda p} \right)}} $ | (2) |
式中:ρ为空气密度,单位:kg·m-3;ρm为砝码密度,单位:kg·m-3;A0为活塞组件在零压力和20 ℃下的有效面积,单位:m2;α为活塞杆和活塞筒的线性热膨胀系数,单位:1/℃;t为活塞组件温度,单位:℃;λ为压力形变系数,单位:1/MPa。
由式(2) 可见,实际工作中活塞压力计所复现的压力与空气密度ρ相关,因此,空气密度ρ及其不确定度将对所复现压力的不确定度产生影响。
2 空气密度计算公式对于实际的湿空气,其空气密度的计算公式[3]如下:
| $ \rho = \frac{{{p_A}{M_a}}}{{ZRT}}\left[{1-{X_V}\left( {1-\frac{{{M_V}}}{{{M_a}}}} \right)} \right] $ | (3) |
式中:pA为环境大气压力,单位:Pa;Ma为干空气摩尔质量,单位:kg;Z为压力为p,温度为T时湿空气的压缩系数;R为气体常数;T为气体绝对温度,单位:K;XV为水汽摩尔分数,按式(4) 计算;MV为水汽摩尔质量,单位:kg。
| $ {X_V} = \frac{e}{{{p_A}}} $ | (4) |
式中e为水汽分压,单位为Pa,其数值可按下式计算。
| $ e = U{p_{sv}} $ | (5) |
式中:U为以小数点形式表示的相对湿度;psv为温度为T时的饱和水汽压,单位:Pa。
根据式(3)~(5),可推导出湿空气密度与环境大气压力、气体绝对温度、气体相对湿度以及当前温度下饱和水汽压的关系,见式(6)。
| $ \rho = \frac{{{M_a}}}{{ZRT}}({p_A} - 0.378U{p_{sv}}) $ | (6) |
将Ma/R=3.48349(1991年CIPM-81公式使用的推荐值)代入式(6),有:
| $ \rho = \frac{{3.48349 \times {{10}^{ - 3}}}}{{ZT}}({p_A} - 0.378U{p_{sv}}) $ | (7) |
通过式(7),可以看出对空气密度标准不确定度分量有影响的量有环境压力pA、温度T、湿度U、空气压缩系数Z。
3 空气密度的标准不确定度u (ρ)PG7607活塞压力计底座安装有环境压力传感器、环境温度传感器及湿度传感器,这些传感器对环境实时测量,实时进行空气密度的计算,进而计算其复现的压力。因为空气密度是环境压力、温度、湿度和空气压缩系数的函数,因此,环境压力、温度、湿度和空气压缩系数的测量不确定度都将影响空气密度的不确定度。表 1给出了在一定环境条件下使用各传感器的测量标准不确定度。根据表 1各传感器使用的环境条件,查湿空气的压缩系数表[3],空气压缩系数Z≈1。可将式(7) 中的Z按1取值。
|
|
表 1 在一定环境条件下使用各传感器的测量标准不确定度 Table 1 The measurement standard uncertainties of various sensors under certain environmental conditions |
| $ {p_{sv}} = {\rm{exp}}(A{T^2} + BT + C + \frac{D}{T}) $ | (8) |
式(8) 中:
A=1.23778847×10-5 K-2,B=-1.9121316×10-2 K-2,C=33.93711047,D=-6.3431645×103 K-1,T为热力学温度,单位:K。
常数A,B,C,D值为1991年CIPM-81公式使用的推荐值,从式(8) 可以看出,饱和水汽压只与温度有关。
3.2 温度测量引入空气密度不确定度分量的计算对式(7) 中T求偏导,有:
| $ \begin{array}{l} \frac{{\partial \rho }}{{\partial T}} = - \frac{{3.48349 \times {{10}^{ - 3}}}}{{{T^2}}}\{ {p_A} + 0.378U{{\rm{e}}^{(A{T^2} + BT + C + \frac{D}{T})}} \times \\ \;\;\;\;\;\;\;\;\;[T(2AT + B-\frac{D}{{{T^2}}})-1{\rm{ }}]\} \end{array} $ | (9) |
对式(7) 中pA求偏导,有:
| $ \frac{{\partial \rho }}{{\partial {p_A}}} = 3.48349 \times {10^{ - 3}}\frac{1}{T} $ | (10) |
对式(7) 中U求偏导,有:
| $ \frac{{\partial \rho }}{{\partial U}} = - 3.48349 \times {10^{ - 3}}\frac{1}{T} \times 0.378{p_{sv}} $ | (11) |
由于环境温度测量分量、压力测量分量和湿度测量分量互不相关,遵循测量不确定度评定与表示中合成标准不确定度的计算公式[6],因此空气密度合成标准不确定度为各分量引入标准不确定度的方和根,见式(12)。
| $ \begin{array}{l} {u_c}\left( \rho \right) = {f_1}(T, {p_A}, U) = \\ \sqrt {{{\left[{\frac{{\partial \rho }}{{\partial T}} \times u\left( T \right)} \right]}^2} + {{\left[{\frac{{\partial \rho }}{{\partial {p_A}}} \times u({p_A})} \right]}^2} + {{\left[{\frac{{\partial \rho }}{{\partial U}} \times u\left( U \right)} \right]}^2}} \end{array} $ | (12) |
通过式(9) 至式(11) 可以看出,uc(ρ)是环境温度T、环境压力pA和环境湿度U的函数。
在表 1所规定的T,pA,U变化范围内,通过MATLAB编程可计算出uc(ρ)的最小值为0.00203 kg·m-3,出现在环境压力为700 hPa、温度为19 ℃及相对湿度为50%的条件下。uc(ρ)的最大值为0.00280 kg·m-3,出现在环境压力为1100 hPa、温度为23 ℃及相对湿度为70%条件下。
在北京地区环境压力在(1000±50) hPa范围、实验室环境温度控制在(20±1) ℃范围、湿度环境控制在50%~70%范围内,通过MATLAB编程可计算出uc(ρ)的最小值为0.00245 kg·m-3,出现在环境压力为950 hPa、温度为19.9 ℃及相对湿度为50%的条件下。uc(ρ)的最大值为0.002685 kg·m-3,出现在环境压力为1050 hPa、温度为21 ℃及湿度为70%条件下。
4 空气密度对压力测量引入的标准不确定度分量ur, ρ(p)空气密度对压力测量引入的标准不确定度分量表示为:ur, ρ(p)=cr, ρ×uc(ρ),即空气密度标准不确定度与它的灵敏系数的乘积[6],其中cr, ρ为灵敏系数。
4.1 空气密度对压力测量标准不确定度灵敏系数cr, ρ的计算对式(2) 中ρ求偏导,有:
| $ \begin{array}{l} \;\frac{{\partial p}}{{\partial \rho }} = - \frac{{mg}}{{{A_0}\left[{1 + \alpha \left( {t-20} \right)} \right]\left( {1 + \lambda p} \right){\rho _m}}}\\ {c_{r, \rho }} = {f_2}({\rho _m}) = \left| {\frac{1}{p} \times \frac{{\partial p}}{{\partial \rho }}} \right| \approx \left| { - \frac{1}{{{\rho _m}}}} \right| = \\ \;\;\;\;\;\;\left| { - \frac{1}{{8000}}} \right| = 125\;{\rm{ppm}}/{\rm{(kg\cdot}}{{\rm{m}}^{{\rm{ - 3}}}}{\rm{)}} \end{array} $ |
cr, ρ为空气密度引入标准不确定度的灵敏系数。
4.2 空气密度对压力测量引入的标准不确定度分量uP的计算| $ {u_{r, \rho }}\left( p \right) = {c_{r, \rho }}{u_c}\left( \rho \right) = {f_2}({\rho _m}){f_1}(T, {p_{A, }}U)\;\;\;\;\;\;\;\;\;\;\left( {k = 1} \right) $ |
ur, ρ(p)最大值为0.35 ppm, 最小值为0.25 ppm。在北京地区,实验室温湿度环境加以控制的条件下,ur, ρ(p)最大值为0.33 ppm,最小值为0.31 ppm。
5 结论(1) 空气密度对于活塞压力计测量结果的影响与使用地点环境大气的温湿压状态有关;与使用地点环境大气温湿压测量结果的不确定度有关。
(2) 在全国范围内,环境压力在700~1100 hPa范围、实验室环境温度控制在19~23 ℃范围、相对湿度环境控制在50%~70%范围内,空气密度对于活塞压力计测量结果的影响在0.25 ppm至0.35 ppm范围内。
(3) 在北京地区环境压力在(1000±50) hPa范围、实验室环境温度控制在19~21 ℃范围、相对湿度环境控制在50%~70%范围内,空气密度对于活塞压力计测量结果的影响在0.31 ppm至0.33 ppm范围内。
值得指出的是,尽管由于空气密度引入的不确定度分量对于PG7607活塞压力计不确定度的贡献仅为8.4%,但是由于对其不确定度有影响的分量包括了砝码、有效面积、重力加速度、空气密度、砝码密度等十几个方面,因此在基标准级计量仪器比对进行不确定度分析时,空气密度分量对压力测量引入的标准不确定度也是不能忽略的。
| [1] |
PTB220 Series Digital Barometers User's GUIDE. Finland: Vaisala Oyj.2001:71-72.
|
| [2] |
鞠晓慧, 任芝花, 曹丽娟, 等. 自动与人工观测气压的差异与原因分析[J]. 气象, 2010, 36(1): 104-110. DOI:10.7519/j.issn.1000-0526.2010.01.016 |
| [3] |
李英干, 范金鹏. 湿度测量[M]. 北京: 气象出版社, 1990: 46-484.
|
| [4] |
Michael Bair, Pierre Delajoud. Uncertainty Analysis for Pressure Defined by a PG7601, PG7102, PG7202 OR PG7302 PISTON GAUGE.DH Instruments, Inc.Technical Note 7920TN01C.1996:10-13.
|
| [5] |
姚弘, 陈利. JJG99-2006砝码检定规程[M]. 北京: 中国计量出版社, 2006: 42-44.
|
| [6] |
李慎安, 施昌彦, 刘风. JJF1059-1999测量不确定度评定与表示[M]. 北京: 中国计量出版社, 1999: 16-18.
|
 2011, Vol. 37
2011, Vol. 37 