引言

1948年信息论创始人Shannon用熵来度量离散随机事件的不确定性，使得不确定性的定量分析有了有效的武器，用条件熵来度量后验不确定性，定义信息是不确定性的减小^[1-3]，在确定和不确定两个对立面之间搭建起桥梁。

检索近期各学科领域(经济学、社会学、会计学、地震、石油、测量、计算机、GIS、水文、法学等)的文献可找到大量有关不确定性的国内外文献，其中不确定性一词介乎习俗语与科学术语之间，其定义、内涵、性质等差异较大，现代更多的学者用来指误差、不精确性、模糊性和含混性。本文所指也是基于这层含义来开展研究，望读者在阅读本文时在概念上不要与天气不确定性(或者不可预报性、可预报性)联系起来，本文中指模式降雨预报结果的不确定性，通过统计多次预报结果得到。而天气不确定性，多采用集合预报方法探讨某一次预报的可能分布情况^[4-8]。

数值天气模式(Numerical Weather Model, NWM)结果存在误差，影响到预报员的判断。对于系统误差，预报员通过一段时间的试用后分析其规律，能有个基本把握，参考时会在头脑中先给予适当订正。而对于随机误差则不同，如果预报结果时大时小，其分布离散度大，就会给人难以把握的感觉，显现出盲目性，预报员参考时越难以把握，其参考价值就小。所以，模式预报结果的系统误差对预报员的干扰处于次要地位，随机误差是主要的。NWM降雨预报结果包含多少盲目的成分, 在多大程度上值得参考是气象学者探讨的一个科学问题。

1 评估指标介绍

统计分析预报量与观测值的误差及误差分布是技术上最成熟的一种方法；TS评分^[9-10]是最流行的方法，也是业务上广泛开展的一项工作，笔者曾开展过尝试^[11]。我们在应用这两种方法的过程中感觉较难从众多计算出的数据中得到非常明确的结论，其结果也包含某些不确定的成分；张学文探讨了熵在气象领域的应用^[12-15]，研究了气象要素的概率分布情况、应用熵原理探讨降雨及其对应面积的关系, 把熵和信息量用于评定预报质量的优劣，这些研究在如何更好地应用信息论上给本文起到了一定的引导作用。但本文在直接应用Shannon不确定性进行计算过程中发现有以下三点问题值得讨论。

(1) 熵量度了概率事件A的先验不确定性，即首先要知道A的概率分布，才能量度不确定性，而A的概率分布需要长期的观测通过统计后才能获得，此时人们已经获得了A的信息，信息量应该大于0。而按信息论推论在采用一种遵从A的概率分布的抽签的方法对A进行预测时信息量为0，对于非均匀概率分布的事件而言不合常理。

(2) 平均交互信息量I或条件熵单独给出时, 多数读者难以理会其意义，只有与该事件的熵(先验不确定性)比较才能对事件有所了解，为什么不能给出已经过比较后更直接、更通俗易懂, 且可比性能更强的不确定性指标呢？

(3) 信息论中条件熵和平均交互信息量等一般针对全概率事件而言。对于复杂事件即使是其某一种特征量，比如日降雨量，要彻底知道其概率分布是很困难的事情；另外，实际应用中我们需要更详细地了解事件在细分区间(如日降雨量的暴雨、大雨、小雨区间，甚至更加细化的区间)上的不确定性特征。

为此我们没有直接照搬Shannon不确定性计算方法，而是调整了研究思路，基于以下几点认识，根据信息论中联合熵，分析其联合熵的最大、最小特征值，通过其处于最大、最小联合熵之间的相对位置设定不确定性指标开展探讨。

2 研究思路及方法 2.1 研究思路

观点1：预报水平(认知程度)高，则不确定性小。

Shannon用信息熵来度量不确定性，由于信息的加入，不确定性减少了，就有了后验不确定性，信息熵也就成了先验不确定性。由此就给了我们启示：针对概率事件的预报，认知程度高时，预报水平高，其中信息含量高，则不确定性小，认知程度低则不确定性大。

如果A的发生概率分布P_i已知时，B为对A进行的预测事件，当对A一无所知时，此时B是一种盲目(或无知)预测, 联合熵将最大，不确定性最大；当B部分包含A的信息, 联合熵将比盲目预测时减小，不确定性比盲目预测时有所减小；当B包含A的全部信息量或者当A被彻底认识后(对复杂系统也许永远无法做到)，试验B的每一结果将对应着A的惟一结果，B与A是一一对应的，那么经过系统误差的订正后对A的预测将可以做到完全正确，B与A是一种确定性的关系，此时尽管A是非常复杂的、信息熵很大，不确定性仍将消失殆尽，人们完全有能力预测A的发生状态。所以不确定性与联合熵之间存在着某种对应关系，好的预报方法联合熵小，不确定性也小；随着信息获取或者说认知程度的深入，其不确定性将会逐渐减小。针对预测行为来说，采用不同的预报方法或不同人(群)做出的预报包含的信息量是不同的，不确定程度也是不同的。

观点2：根据联合熵及其最大最小特征值可以设定指标来定量描述不确定性。

用日降雨量的观测和预报值构成的二维连续随机变量，那么联合熵是预报方法(或模式)的泛函，不同的预报方法将有不同的联合概率密度函数，其联合熵和不确定性也不同。通过下文中对几种典型预报方法联合熵的推导和讨论知道：联合熵在任何子域内都存在最大、最小值，那么某一种预报方法的联合熵处于最大、最小值之间的相对位置就可以定量地描述预报与观测值间的不确定性，用百分制的形式设定这种不确定性指标，其形式简单直观、通俗易懂。我们用它来比较不同模式(或预报方法)之间及不同预报区间的不确定性，可以定量分析各种预报方法或模式预报结果的可参考程度，间接评价其预报性能。

2.2 几种特例下联合熵计算及降雨预报结果不确定性指标引入 2.2.1 连续函数的联合熵

x为降雨量的观测记录，x∈[X_s, X_e]，根据历史气象资料可以统计出x的边缘概率密度函数ρ(x)，图 1给出了2003、2004年6—9月间我国有降水记录观测站降雨量平均概率密度(纵轴)随降雨量x(横轴)的变化情况，与x呈现出负的自相关性，x越大出现概率越小，当x≥27时出现概率低于1%，当x≥58时出现概率低于0.1%。

y为对x的模式预报结果，y∈[0, Y_e]，x和y便构成了一个二维空间集合V，在V内二维连续随机变量(x, y)的联合概率密度函数为ρ(x, y)，满足P_V=∬_Vρ(x, y)dxdy=1。对于降雨而言由于x→0时概率密度函数将很大，故以集合(x∈[X_s, X_e], y∈[Y_s, Y_e])为研究对象(下文中取X_s=Y_s=1), 记ρ₀=P(x≤X_s)/(X_s-0) 为实际日降雨量在0到X_s间的平均概率密度，根据观测降雨量资料计算可得。在某一子集W内事件发生的联合概率为P_W=∬_Wρ(x, y)dxdy，W内的条件概率密度函数为ρ(x, y|W)=ρ(x, y)/P_W，满足P_W=∬_Wρ(x, y|W)dxdy=1。

连续变量的熵虽然形式与离散变量类似，但意义及使用上有区别，所以信息论中称相对熵，对于二维连续变量，联合熵(也称共熵)应称联合相对熵，以下仍简称联合熵。

集合V内事件发生的联合熵为H=-∬_Vρ(x, y)lnρ(x, y)dxdy。

定义子集W事件发生的联合熵与之相似为H_W=-∬_Wρ(x, y|W)lnρ(x, y|W)dxdy。

如果某一预报方法其联合熵比其他方法都大(小)，此时称最大(小)联合熵。

仅针对x或y的情况下概率密度是边缘概率密度函数，其一维熵称边缘熵。

在下面2.2.2节到2.2.5节中推导了几种特殊情况下函数域W内的联合熵H值，推导结果用于分析讨论H的某些特性。推导中为了积分运算的方便，以观测降雨的边缘熵ρ(x)与x的平方呈反比为假设函数，其他地方均不使用这样的假设函数。

2.2.2 盲目(或无知)预报

假设预报是按照随机抽签做出的，且签的概率分布是均一的，在函数区间内平均分布，此时预报是盲目的，不科学的，也是最无知的。其概率密度函数在y方向区间 y∈[Y_s, Y_e]内是均匀分布的，则ρ(x, y)=ρ₀/(Y_e-Y_s)x², 于是联合熵为：

$ \begin{align} &{{H}_{1}}=-\iint_{V}{\frac{{{\rho }_{0}}}{({{Y}_{e}}-{{Y}_{s}}){{x}^{2}}}\text{ln}\frac{{{\rho }_{0}}}{({{Y}_{e}}-{{Y}_{s}}){{x}^{2}}}\text{d}x\text{d}y} \\ &\ \ \ \ \ =-\iint{{}_{{{X}_{0}}}^{{{X}_{e}}}\frac{{{\rho }_{0}}}{{{x}^{2}}}\text{ln}\frac{{{\rho }_{0}}}{({{Y}_{e}}-{{Y}_{s}}){{x}^{2}}}\text{d}x} \\ &\ \ \ \ \ =-{{\rho }_{0}}\left[\frac{\text{ln}{{\rho }_{0}}/\left( {{Y}_{e}}-{{Y}_{s}} \right)}{x}-2\frac{1+x\text{ln}x}{{{x}^{2}}} \right]_{{{X}_{s}}}^{{{X}_{e}}} \\ \end{align} $

当X_e≫X_s时，

$ {{H}_{1}}\approx {{\rho }_{0}}(2+\text{ln}{{Y}_{e}}-\text{ln}{{\rho }_{0}})={{H}_{4}}+{{\rho }_{0}}\text{ln}{{Y}_{e}} $

(1)

2.2.3 按照概率分布的随机预报

假设预报也是按照抽签做出的，但签的概率分布不是均一的，而是遵从观测降雨的发生概率，即降雨量小的签多，而降雨量大的签少，实际发生概率高的区间预报次数多，低的区间预报次数少，并满足概率密度函数与y的平方呈反比，那么二维区间上的概率密度函数为ρ(x, y)=ρ₀/x²y², 于是联合熵为：

$ \begin{align} &{{H}_{2}}=-\iint_{V}{\frac{{{\rho }_{0}}}{{{x}^{2}}{{y}^{2}}}\text{ln}\frac{{{\rho }_{0}}}{{{x}^{2}}{{y}^{2}}}\text{d}x\text{d}y} \\ &\ \ \ \ \ =-{{\rho }_{0}}(\frac{4+2\text{ln}x+2\text{ln}y-\text{ln}{{\rho }_{0}}}{xy})\left| \begin{matrix} {{Y}_{e}} \\ {{Y}_{s}} \\ \end{matrix} \right|\begin{matrix} {{X}_{e}} \\ {{X}_{s}} \\ \end{matrix}~ \\ \end{align} $

当X_e≫X_s=1, Y_e≫Y_s=1时,

$ {{H}_{2}}\approx {{\rho }_{0}}(4-\text{ln}{{\rho }_{0}})={{H}_{4}}+2{{\rho }_{0}} $

(2)

其中H₄见2.2.5节。

2.2.4 实际预报情况的近似

对于一段时间的模式预报样本，可以求得某一单位降雨量观测值区间(x, x+1]内的预报均值${{\bar{y}}_{x}}$和均方差${{\sigma }_{x}}=\sqrt{\sum\limits_{i=1}^{i=n}{{{\left({{y}_{i}}-{{x}_{i}} \right)}^{2}}/n}}$。借用实验物理学中系统偏差和随机偏差的概念，那么$\left| {{{\bar{y}}}_{x}}-\bar{x} \right|$为预报系统偏差，σ_x反映预报随机偏差。

下面计算预报在${{{\bar{y}}}_{x}}$周围±σ_x范围内均匀分布情况下的H，为了计算方便近似假设σ_x与x无关，为一常数，于是概率密度函数为：

$ \left\{ \begin{align} &\rho \left( x, y \right)={{\rho }_{0}}/2{{\sigma }_{x}}{{x}^{2}}\ \ \ \ \ \ \ \ \ \ \ \ \left( \left| y-x \right|\le {{\sigma }_{x}}时 \right) \\ &\rho \left( x, y \right)=0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( \left| y-x \right|>{{\sigma }_{x}}时 \right) \\ \end{align} \right.\ $

此时联合熵为：

$ \begin{align} &{{H}_{3}}=-2{{\sigma }_{x}}\int_{{{X}_{0}}}^{{{X}_{e}}}{\frac{{{\rho }_{0}}}{2{{\sigma }_{x}}{{x}^{2}}}\text{ln}\frac{{{\rho }_{0}}}{2{{\sigma }_{x}}{{x}^{2}}}\text{d}x} \\ &\ \ \ \ \ \ \ =-{{\rho }_{0}}\left[\frac{1}{x}(\text{ln}\frac{{{\rho }_{0}}}{2{{\sigma }_{x}}}-2-2\text{ln}x) \right]_{{{X}_{s}}}^{{{X}_{e}}} \\ \end{align} $

当X_e≫X_s=1时,

$ ~{{H}_{3}}\approx {{\rho }_{0}}(2-\text{ln}{{\rho }_{0}}+\text{ln}2{{\sigma }_{x}})={{H}_{4}}+{{\rho }_{0}}\text{ln}2{{\sigma }_{x}} $

(3)

2.2.5 完全正确的预报

假设有一种很完美的预报方法，能够做到每一次发布的预报值x都能与观测记录y吻合(x=y)，预报100%正确，那么概率密度函数在x≠y时为0，则有：

$ \rho \left( x, y \right)=\left\{ \begin{align} &{{\rho }_{0}}/{{x}^{2}}\ \ \ \ \ \ \ \ \ \left( x=y时 \right) \\ &0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( x\ne y时 \right) \\ \end{align} \right.\text{ } $

此时联合熵为：

$ {{H}_{4}}\approx -\int_{{{X}_{s}}}^{{{X}_{e}}}{\frac{{{\rho }_{0}}}{{{x}^{2}}}\text{ln}~\frac{{{\rho }_{0}}}{{{x}^{2}}}\text{d}x=-{{\rho }_{0}}\left[\frac{\text{ln}{{\rho }_{0}}}{x}-2\frac{1+\text{ln}x}{x} \right]_{{{X}_{s}}}^{{{X}_{e}}}}~ $

当X_e≫X_s=1时,

$ {{H}_{4}}\approx {{\rho }_{0}}(2-\text{ln}{{\rho }_{0}})~ $

(4)

还有另外一种情况下其联合熵与H₄相等，那就是预报并不完全正确，只要x与y满足一一对应的关系，此时预报结果仅包含系统偏差，随机偏差为0。

2.2.6 相关特性分析

通过上面推导过程及结果不难得出以下结论：

(1) 有界区间内分布的事件概率分布的区间越大H越大，均匀概率分布时H最大^[3]。

(2) 比较式(1)、(2)、(3)、(4)，H₁，H₂，H₃和H₄中H₄最小，正确预测的联合熵最小，它与观测降雨量的边缘熵是等同的，盲目预报的联合熵H₁最大。任何模式的联合熵H将在H₄和H₁间变化，满足H₁≥H≥H₄。H₄代表了最小联合熵，H₁代表了最大联合熵。盲目预报是最差的预报方法，其联合熵最大；完美的预报在实际中很难做到，其联合熵最小。

(3) H₃与y方向上概率分布有关，主要是模式预报随机偏差的影响，当σ_x越大时H₃越大，而与(x, x+1]区间预报结果的平均值${{{\bar{y}}}_{x}}$无关，即与预报系统偏差$\left| {{{\bar{y}}}_{x}}-\bar{x} \right|$无关。

2.2.7 降雨预报结果不确定性指标引入

如果某数值天气模式试验期内联合熵为H，最大、最小联合熵分别为H_max，H_min，定义不确定性指标U为H位于H_max，H_min之间相对的相对位置，表示为：

$ U = \frac{{H - {H_{{\rm{min}}}}}}{{{H_{{\rm{max}}}} - {H_{{\rm{min}}}}}} \times 100\% $

(5)

其中：

$ \begin{align} & \\ &\begin{matrix} H=-\iint_{W}{\rho \left( x, y \right)\text{ln}\rho \left( x, y \right)\text{d}x\text{d}y} \\ {{H}_{\text{max}}}=-\iint_{W}{\frac{\rho \left( x \right)}{({{Y}_{e}}-{{Y}_{s}})}~\text{ln}\frac{\rho \left( x \right)}{({{Y}_{e}}-{{Y}_{s}})}\text{d}x\text{d}y} \\ {{H}_{\text{min}}}=-\int_{{{X}_{s}}}^{{{X}_{e}}}{\rho \left( x \right)\text{ln}\rho \left( x \right)\text{d}x} \\ \end{matrix} \\ \end{align} $

U是通过统计模式降雨预报结果与观测降雨量之间的联合熵，其相对于盲目预报和完美预报(或能与观测降雨量形成一一对应关系的预报)之间的相对百分制大小，代表了模式预报所包含盲目性大小的程度，它可以定量地反映数值模式降雨预报结果的不确定性，本文称之为降雨预报结果不确定性指标，针对某一区间其值与预报结果的统计特征量——离散度有着紧密联系，离散度越小，U越小，反之亦然。根据上述对H₃的讨论，H₃与随机偏差σ_x有关，而与系统偏差$\left| {{{\bar{y}}}_{x}}-\bar{x} \right|$无关，因此可以说数值模式预报结果的不确定性与随机偏差密切相关而与系统偏差无关。假设统计样本中预报与观测记录一一对应，U与预报完全正确时的不确定性指标相同为0%，预报的可确定程度为100%，完全克服了预报的盲目性；当模式预报的不确定性指标大时，预报结果忽大忽小，给人难以把握的感觉，其分散的区间越大或离散程度越高，盲目性越大，预报员参考时越难以把握模式的预报性能，其参考价值越小，一种特例是当预报在y方向均匀分布时，是盲目预报或称无知的预报，U=100%，预报的不确定性最高，此时的预报毫无意义。U越小的预报模式包含的随机偏差越小，即使其预报评分较低，如果对其进行系统偏差订正后预报评分就能得到明显改善，那么其可供参考性仍然较强，对天气预报的指导意义更大。

在3.3节讨论中可以知道：H₃与预报系统偏差$\left| {{{\bar{y}}}_{x}}-\bar{x} \right|$无关，不包含预报准确程度的信息。所以U或者H并不能用来检验模式预报效果和准确率，U可以用来评价模式预报结果的可参考程度，从而间接分析模式的预报性能。

3 实例计算与初步研究结果

我们对T213、日本RSM在2003、2004年6—9月对我国短期降雨预报情况进行了统计和计算，以期能定量描述各模式降水预报结果的不确定性。其中T213预报资料为国家气象中心下发的1°网格距资料，日本RSM资料网格距为1.25°；通过双线性内插由模式网格资料得到观测站降水预报值；模式初始时刻均为北京时间08时，模式预报时段均为起报时刻后24小时。

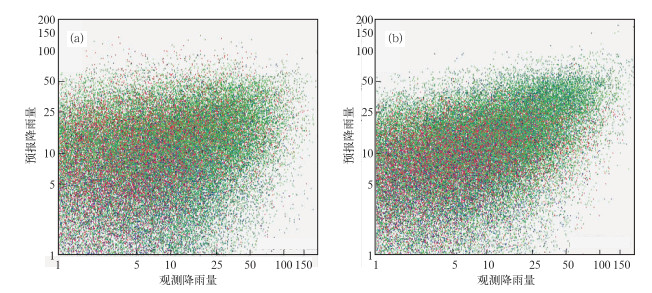
3.1 模式降水预报能力定性分析

图 2给出了2003、2004年6—9月模式对我国降雨的预报相对观测记录的散点图，其中图 2a为T213模式，图 2b为日本RSM。从图中可以定性地比较分析模式预报的不确定性，得到一定的感性认识：(1) 模式降水预报结果离观测记录存在较大的差异，两种模式预报结果都包含随机偏差，存在较大的不确定成分；(2) 模式降水预报结果与观测记录之间不是完全独立的，存在某种联系，在相对中轴曲线附近存在某种概率分布规律；(3) 两种模式降水预报系统偏差的分布规律都存在对小降水预报偏大，而对强降水预报偏小的现象；(4) T213模式预报结果的离散程度比日本RSM偏大，其随机偏差也相对偏大。

3.2 不确定性指标计算步骤简要介绍

取Y_e=150，X_e=200，单位为mm/d。集合V:x∈[X_s, X_e]，y∈[Y_s, Y_e], 子集W:x∈[X_s, X_e], y∈[Y_s, Y_e]。ρ(i, j)分段概率密度函数，ρ(x, y)为概率密度函数，ρ′(x, y)为概率密度的估计函数。

(1) 统计计算中取分段的区间长度为1 mm，预报降雨量O和观测降雨量F分段区间i < O≤i+1、j < O≤j+1上时，统计出现的次数N(i, j)，由此可得到V内离散的概率分布情况P(i, j)。

(2) 由于分段的区间长度为1，故${\hat{\rho }}$(x, y)=p(i, j)；

(3) 将${\hat{\rho }}$(i, j)用数学函数近似模拟，得到ρ′(x, y)。在一维函数逼近中我们采用负指数、Γ函数、对数正态与Weibull函数分别进行了试验，最后对x方向分布选用Γ函数，对y方向选用对数正态函数，得出的二维概率密度模拟函数表达式为：

$ \begin{align} &\rho \prime \left( x, y \right)=C{{x}^{-m}}\text{exp}\left( -ax \right)\cdot \frac{b}{y}{{x}^{E}}\times \\ &\text{exp}\left[-\frac{1}{2}{{\left( \frac{10\text{ln}by-d}{\sigma } \right)}^{2}} \right] \\ \end{align} $

式中σ=Dx^-E, d=Alnx-B, 各项参数由表 1给出。

(4) 在N(i, j)≥4时ρ(i, j)=${\hat{\rho }}$(i, j)；在出现概率小的区间统计出来的经验概率密度将包含有较大的随机性，我们认为其并不能代表实际的分布情况，因此对经验概率较小和小的统计数据将根据ρ′(x, y)给予适当的订正：在N(i, j)=0的区域ρ(i, j)=ρ′(x=i, y=j)；在N(i, j)= 1，2，3时ρ(i, j)=[${\hat{\rho }}$(i, j)+ρ′(x=i, y=j)]/2。

(5) 对于不同x取值范围，由ρ(i, j)计算在各子集上的H_max，H，H_min和U。

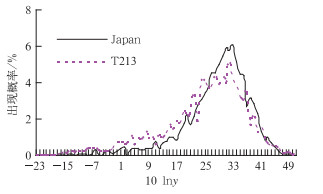
3.3 计算结果分析

图 3以观测站日降雨量x∈(9, 10]时为例给出了模式降雨预报值y的出现概率变化情况。图中虽然10lny在33附近(y∈(27.1, 30.0])出现峰值，NWM减小了预报的盲目程度，对天气预报员具有指导意义，体现出天气的可预报性；同时我们不得不承认该峰值所对应的概率很小，T213和日本模式分别对应为6.1%和5.1%，半分布区间长度(文献[16、17]提到可以量度不确定性)分别约为19和24 mm。模式预报结果的这种概率分布特性在一定程度上使预报员在参考模式预报结果时有时会感觉到模式预报的盲目性，这种盲目性依赖于模式预报结果的随机偏差(或是离散度)，是模式预报结果不确定的根本原因。

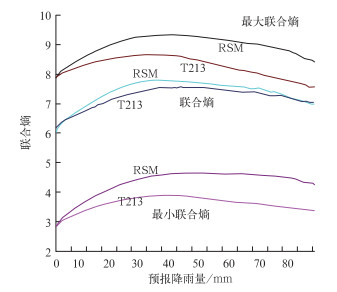
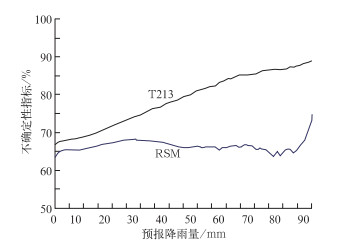
图 4给出了模式0~24小时降水预报在不同取值Y下W区间内的最大联合熵、联合熵、最小联合熵(纵轴)随Y(横轴)的变化曲线，各模式上中下3条曲线分别代表H_max，H和H_min。最小联合熵是与观测值的边缘概率密度分布有关，完全由观测资料决定，与预报无关，如果预报对象选取的日期完全相同，那么两种模式应该是相同的，针对相同事件同样的统计样本时，联合熵已经具有了表征预报不确定性的能力，只不过可比条件具有局限性，采用不确定性指标就放宽了可比条件。实际计算过程中由于资料收集等原因，两种模式在实验期中缺少资料的日期不尽相同，预报样本的日期将有某些微小的差别，并不是完全一一对应的，因此，两种模式预报的最大、最小联合熵是有区别的。图 4中两者的最大(最小)联合熵是不相等的，使得联合熵可比性受到限制，而不确定性指标U反映联合熵处于最大最小联合熵之间的相对位置，具有了可比性。图 5给出了两种模式不确定性指标的计算结果，两种模式预报的不确定性指标都超过了60%，就是说目前的NWM很大程度上具有不确定性，模式降水预报结果与实况降雨存在较大的系统偏差和随机偏差。同时联合熵小于最大联合熵，使得降水预报的不确定性指标小于100%，减小了预报的盲目性，才使得预报变得有意义。另外，虽然图 4中两种模式的联合熵相差不大，但由于最大(最小)联合熵的不同，两者不确定性指标却存在明显差距，从图 5可以看出，日本RSM预报(细线)的不确定性比T213(粗线)小，就是说对我国24小时降水预报日本RSM随机偏差较小，预报结果含有更多的信息量，对天气预报的指导意义也大。特别是日本RSM预报有40~80 mm降水的时候，预报员可能要给予加倍的关注，因为从图中可以看到日本RSM在此区间的不确定性指标相对偏小。针对这一点我们进行过预报效果检验，日本RSM在中雨和大雨量级上的预报Ts评分高、漏报率低。对于T213，预报降水越大，其不确定性指标越大，在强降雨预报方面有待进一步提高。

4 结论

(1) 为了定量表述数值模式预报的不确定性，本文应用信息论联合熵，在分析最大最小联合熵基础上，根据联合熵相对于最大最小联合熵的位置设定不确定性指标U，它代表了模式预报结果所包含盲目性大小的程度。U与模式预报随机偏差有着紧密联系，即与预报随机偏差的离散度有关，U越小的预报结果包含的随机偏差离散度越小，模式预报结果含有更多信息量，对天气预报的指导意义越大；但U与模式预报的系统偏差无关，并不是模式预报效果检验的指标。

(2) NWM可以减小天气预报的盲目程度，对天气预报员具有指导意义；同时NWM在日降水预报方面仍然在很大程度上具有不确定性，U超过60%，天气预报员在参考时要对模式的预报性能要有全面的了解与深入的分析，盲目的跟从是不可取的。

(3) 针对2003、2004年汛期两种数值预报模式计算了不确定性指标U，对我国大陆范围24小时降水预报而言，日本模式比T213不确定性小，特别是日本RSM预报在出现40~80 mm降水时比T213具有更高的参考价值。

5 讨论

(1) 研究中资料年限不够长，计算结果所反映的某些细节特征不可避免与真实情况存在一定差异，特别是对于发生概率较小的区间可能会出现相对大的计算误差。

(2) 文中为计算方便人为假设了降雨量观测和预报的上界，实际上该界限是很难确定的。

(3) 本文在近似条件下探讨了系统偏差和随机偏差对不确定性的影响，预报的系统偏差和随机偏差并不能严格区分，而且实际的概率分布函数是非常复杂的，所以本文U与随机偏差有关而与系统偏差无关的结论难以给出严格的数学证明。

(4) 数值预报模式对不同气候特征及地域预报能力会有所不同，对不同尺度降雨系统也不同，其误差的分布就存在地域差异和尺度差异，本文中为了增加样本量，把不同地域的降水预报笼统地进行分析计算，值得商榷。