长江流域、江南和华南地区是我国夏季高温热浪袭击的重灾区,一般年份都会出现20~30天的高温天气,梅雨期短的年份高温日数可超过40天。持续性高温还给人们的健康造成危害,甚至危及生命,这时夏季高温的提前预报就显得特别重要。目前有关高温的研究主要有高温的气候特征[1-5]、高温的环流形势及成因和高温的预报,如缪国华等[6]、邹燕等[7]应用高空高度场资料,分别分析了江苏苏州市的多高温年和少高温年的前期环流特征和造成福建省高温过程的主要天气系统及形势特征。张迎新等[8]、贺哲等[9]分别进行了2009年华北平原大范围持续高温过程成因和郑州极端高温天气成因分析。有关高温预报方面的研究也从不同角度进行过尝试和研究,赵金彪等[10]、陈丽华等[11]曾分别探讨了夏季高温预测方法和高温形成机理研究。刘梅等[12]利用数值预报和实况开展了江苏省夏季最高温度定量精细化预报方法研究,这些研究都从不同出发点对夏季高温进行了预报。而关于气温和海温、海冰关系的研究也有专家进行过探讨,如何卷雄等[13-14]分析了江苏冬夏极端气温与大气环流及海温场的遥相关。方茸等[15]探讨了中国夏季高温与北极海冰的联系特征。综合有关高温各方面的研究发现高温的发生受到多种因素的影响,各地区间也存在着较大差异,而长江流域一带高温的发生和大气环流中的大陆高压、副热带高压(简称副高)有着紧密的联系,而副高、大陆高压的演变又与海温有着一定的反馈关系[16-17],海温对大气环流的影响具有一定的滞后性,研究发现赤道附近暖水区海温的变化对副高的动态具有一定的可预报性,因此考虑海温与高温的发生可能具有一定的关系。而目前关于高温日数与海温的分析以及利用海温相关进行高温日数的预报目前涉及较少,本文即在两者场相关分析基础上,利用西太平洋海温作为长期预报因子开展江苏夏季逐月高温日数的预报,建立长期预报模型。该研究成果将对高温的早期预报及社会服务具有重要意义,特别是医疗、农业、电力、商业等领域的应用更加可观。
1 资料与研究方法 1.1 资料逐月高温日数资料是利用1978—2007年30年资料统计结果,江苏多年出现高温时段一般在6—8月,有些年份9月也有高温出现但时间短强度较弱,因此本文主要利用区域平均方法计算了江苏不同区域6—8月高温日数的区域平均值,并根据江苏高温日数气候分布规律,划分为江苏西北部、东北部、江淮之间和沿江苏南四个区域分别进行研究分析。
海温场资料选择1978—2007年中上一年1月至当年7月10°S~50°N、120°E~80°W太平洋海区5°×5°格点(共286个)的海平面温度(SST)资料,分析其与江苏夏季高温日数之间的关系。
1.2 研究方法 1.2.1 区域平均方法根据1996年Jones等提供的用经纬度网格面积加权平均[18]来计算某一气候要素区域平均值,建立了江苏不同区域高温日数平均值的时间序列,以计算其与西太平洋海温的相关性。计算公式如下:
| $\bar x = \frac{{\sum\limits_{i = 1}^n {\left( {{\text{cos}}{a_i} \times \frac{1}{k_i}\sum\limits_{j = 1}^{{k_i}} {{x_j}} } \right)} }}{{\sum\limits_{i - 1}^n {{\text{cos}}{a_i}} }}$ | (1) |
式中,x为要素x的区域平均值,n为网格数,ai(i=1, 2, …, n)为每个网格的中心点纬度,xj(j=1, 2, …, ki)为区域中某一网格内参与计算的ki个点的气候要素值。
在相关海区预报因子的选取中为了避免单相关的偶然性,根据场相关分析原理,应用了拓扑方法,实现了连片海温场的相关分析,剔除单个高相关的因子,以存在连续4个以上相关显著格点的海区作为1个相关显著区,并取区内格点海温的平均值作为1个预测因子。
1.2.2 最优化相关处理技术考虑单用相关区格点海温的平均值作为自变量建立的预测模型,其拟合和预报效果不一定达到最佳,为了取得更加显著的相关效果,本文还采用了最优化相关处理技术[19],将相关区内格点海温的平均值进行最优化处理。并在最优化和普通回归方程中选择效果最好的模型作为该区域的预测模型。
在建立回归模型中关键是预报因子的挑选, 过程中可以对预报因子格点海温进行线性相关普查和非线性的相关普查。但由于受函数形式的限制,有时不能找到最优的表达形式,故有人提出使用xa和eax两种通式,利用最优化方法确定参数a,能大大提高因子的相关系数。研究结果也证明在一定区间内lnx, eax, ax2+bx+c与预报量y的相关系数均小于或接近于xa与y的最优相关系数,因此本文采用简单的幂函数形式。在最优化处理技术中因子X的线性和非线性化处理可归纳为一种通用变换形式[19]:
| $X' = {\left( {\left| {X - b} \right|/B + 0.5} \right)^a}$ | (2) |
式中,a和b为待定参数,且Xmin≤b≤Xmax,B=max(Xmax-b, b-Xmin)。经上式变换后,X′与Y(Y为因变量)必为单调关系,且(│X-b│/B+0.5) 的值在区间[0.5, 1.5]内变化。a值,一般在(-10, -1/10) 和(1/10, 10) 区间内取值,b值以Xmin+(Xmax-Xmin)/4≤b≤Xmax-(Xmax-Xmin)/4为宜。待定参量a和b可用最优化技术求出。目标函数为:
| $f\left( {a,b} \right) = 1 - {R^2} = {\text{min}}$ | (3) |
R为a和b取一定值时, X′与Y的相关系数。应用二维寻优的变量转换思路将其分解为一元问题逐步处理[20]。该方法处理后获得的结果,是与因变量高温日数相关最显著的因子。
2 不同区域夏季逐月高温日数与西太平洋海温关系分析利用不同区域高温日数与太平洋海温资料分别计算了各区域的场相关,并进行了相关分析和因子选取,由于篇幅限制本文中仅给出江苏西北部夏季逐月高温日数与太平洋海温的相关分析。
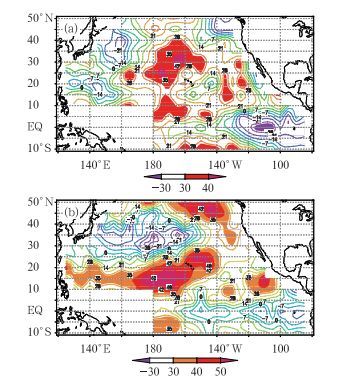
在西太平洋海温和江苏西北部6月高温日数的相关分析中,上一年1—8月都有一定的相关区域,但不稳定且显著性也较差,9月份相关较为明显,通过0.05显著性水平检验的正相关区位于30°N附近的太平洋中部区域(见图 1a)。最稳定显著的相关出现在上一年12月至当年5月,该时段通过0.05显著性水平检验的两个正相关区分别位于10°~25°N附近的太平洋中部和东北太平洋区域(见图 1b), 相关系数达0.4~0.5,有些区域通过0.01显著性水平检验(文中图 1~2所显示数据是相关系数百分率)。
|
图 1 江苏西北部地区6月平均高温日数与太平洋海温相关图(单位:%)(a)上年9月,(b)当年5月 阴影区通过0.05显著性水平检验 Fig. 1 Correlation analyses between average high temperature days in June in the northwest of Jiangsu and the West Pacific SST (unit: %) (a) September last year; (b) May this year The shaded areas are those with the confidence level passing 0.05 |
|
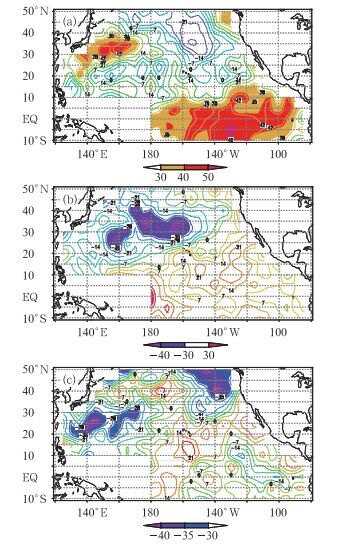
图 2 江苏西北部7和8月高温日数与太平洋海温相关图(单位:%)(a)7月高温日数与上年12月海温,(b),(c)8月高温日数与当年1月、上年4月海温 阴影区通过0.05显著性水平检验 Fig. 2 Correlation analyses between high temperature days (HTD) of July and August in the northwest of Jiangsu and the West Pacific SST (unit: %) (a) HTD of July and SST of December last year, (b) HTD of August and SST of January this year, and (c) HTD of August and SST of April last year The shaded areas are those with the confidence level passing 0.05 |
西太平洋海温和江苏西北部7月高温日数具有很好的相关,正的高相关区主要出现在上一年4月到当年2月的赤道附近太平洋中东部区域,相关范围呈明显的东西带状分布,该高相关区稳定显著。另外上一年12月至当年5月在西北太平洋区域也有一块稳定显著的正相关区,相关系数为0.4~0.5,并通过0.05显著性水平检验。图 2a给出了上年12月海温与7月高温日数的相关图,整个时段的负相关不明显,且区域小而不稳定。
8月高温日数和太平洋海温相关分布中具有明显的负相关关系,显著正相关基本不存在,从上一年1月至当年5月在北太平洋区域存在通过0.05显著性水平检验的负相关关系,最为显著稳定的时段出现在上年12月至当年5月,负相关区主要位于35°N附近的西太平洋中部和中西部海区(见图 2b)。上年1—4月也存在显著的负相关,但相关区域有所变化,显著区分别位于西北太平洋区域和东北太平洋地区(见图 2c)。可见北太平洋海温对江苏西北部8月的高温日数具有一定的反相关预报意义。
根据江苏西北部不同月份与太平洋海温的相关分析发现,不同月份两者的相关程度、相关区域范围和持续的时间都存在着明显差异,6和7月高温日数和太平洋海温存在明显的正相关,但正相关区域不同,6月高温日数的高相关海区位于太平洋中部,7月则位于NINO3和NINO4区(5°N~5°S、170°~120°W);而8月高温日数与太平洋海温无明显正相关区,仅在太平洋北部西风漂流区出现负相关。同一区域3个月的相关差异决定了选择逐月建立高温预测模型的合理性。
根据江苏不同区域高温日数和太平洋海温相关分析发现,不同区域之间存在着很大的差异,太平洋海温对沿江苏南地区高温日数有明显的正相关,相关区集中而相关程度较大。而对江苏东北部地区则有明显的负相关,而且相关区域零散。对江淮地区和江苏西北部则正负高相关区都存在。总体来看赤道附近NINO3和NINO4区海温对江苏不同月份的高温日数以正相关为主,太平洋中北部海温对江苏高温日数则以负相关为主,中部也存在一些正相关。可见不同区域不同月份的高温日数预测模型有着不同的预报因子。
3 江苏不同区域夏季高温日数的长期预报模型据以上分析, 西太平洋地区的海温对江苏夏季逐月高温日数出现有显著的影响, 因此可以通过前期海温场资料对江苏省夏季逐月高温日数进行预报。经最优化相关处理后的高相关海温因子,自变量组合起到非奇异效果。同时利用逐步回归方法,分别建立了稳定可靠的江苏西北部、东北部、江淮和沿江苏南夏季逐月区域平均高温日数预测模型。其中,江苏东北部和沿江苏南的8月最优化后的预报效果没有直接进行逐步回归建立模型的相关效果显著,采用了直接的逐步回归模型。各区域具体模型结果如下。
3.1 江苏西北部夏季逐月高温日数预报模型6月:Y1=-5.357 + 2.6X1′+ 0.82X2′+0.36X3′-0.88X4′+ 0.55X5′+ 3.32X′6
(F=31.3, R=0.96)
7月:Y2=5.9-0.52X1′-2.13X2′-0.23X3′+ 0.14X4′+0.65X5′ (F=21.76,R=0.91)
8月:Y3=-3.87-0.06X1′+1.25X2′+0.52X3′-0.89X4′-0.28X5′+0.95X6′+2.93X7′ (F=28.21, R=0.95)
式中, Y1,Y2和Y3分别代表江苏西北部夏季6、7、8月区域平均高温日数,Xi′为最优化处理后的预测因子。其中最优化处理前后Xi和Xi′之间的关系以及各预测因子所代表的海区见表 1。
|
|
表 1 江苏西北部6、7、8月预测因子优化处理关系及所代表的时间区域 Table 1 The optimal processing relation of predictors and corresponding time and region about models of June, July and August in Northwest of Jiangsu |
考虑文章篇幅限, 在此仅给出沿江苏南、江苏东北部和江淮地区预报模型结果,具体优化关系和每个因子所代表海区、时间不在此列出。
6月:Y=0.882+0.59X1′+0.01X2′-0.96X3′+ 0.81X4′ (F=21.9,R=0.88)
7月:Y=-31.59 +0.32X1′-0.25X2′-3.23X3′+61.26X4′-18.05X5′
(F=21.15,R=0.90)
8月:Y=-163.69-0.18X1′+0.34X2′+0.28X3′-0.35X4′+0.14X5′+0.24X6′
(F=13.94,R=0.89)
江苏东北部:
6月:Y1=5.76-16.9X1′+10.04X2′+0.002X3′+1.04X4′+0.34X5′
(F=20.39, R=0.92)
7月:Y2=-5.501-0.15X1′+0.84X2′+4.07X3′+1.17X4′ (F=19.56, R=0.87)
8月:Y3=89.98-0.04X1′-0.05X2′-0.24X3′+ 0.07X4′-0.124X5′ (F=18.38, R=0.89)
其中,Y1, Y2和Y3分别代表江苏东北部夏季6、7、8月区域平均高温日数,Xi′为最优化处理后的预测因子。
江淮地区:
6月:Y=-56.8+27.78X1′+0.23X2′+1.48X3′+0.38X4′+0.03X5′+27.62X6′
(F=24.6,R=0.94)
7月:Y=-7.75+2.67X1′+5.39X2′+1.68X3′+0.03X4′ (F=31.16,R=0.91)
8月:Y=5.84-33.86X1′+25.85X2′+1.13X3′+24.34X4′-19.56X5′-0.42X6′
(F=16.74,R=0.90)
其中,Y1,Y2和Y3分别代表江苏江淮地区夏季6、7、8月区域平均高温日数,Xi′为最优化处理后的预测因子。
3.3 优化前后模型结果分析为说明验证采用最优化处理后所建预报模型的优势,对不同地区、不同月份优化处理前后模型复相关系数和F检验值进行了列表对比分析(见表 2),明显看出除沿江苏南8月优化后结果没有优化前模型效果显著外,其他优化处理后模型效果都明显好于优化前,表现在模型复相关系数得到了明显提高,如江苏西北部6和8月、江淮6—8月、沿江苏南6月优化后预报模型复相关系数提高了10%~30%。F检验值也是明显大于优化前模型的F值。因此在本研究中采用最优化方法建立预报模型具有其明显优势,大大提高了预报模型效果。
|
|
表 2 优化处理前后预报模型检验值对比 Table 2 The comparison of test values in forecast model before and after optimal processing |
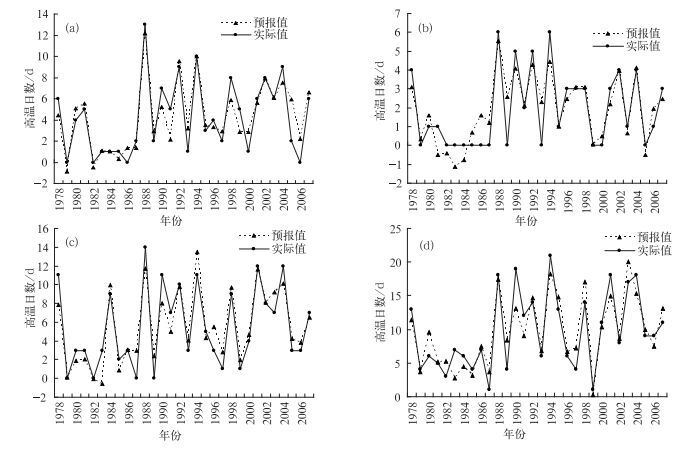
利用上述预报模型进行回代检验,分析了江苏夏季不同区域不同时段区域平均高温日数的拟合结果,因篇幅限制在此仅给出不同区域夏季7月预报模型的拟合情况(图 3)。可以看出模型的历史拟合效果较好,大部分年份模型的模拟值和实际值十分吻合,有些年代存在一定的误差,但所反映的趋势和实况比较吻合。所有模型都通过了α=0.01的显著性检验。
|
图 3 江苏不同区域夏季7月区域平均高温日数模拟结果 (a)西北部,(b)东北部,(c)江淮,(d)沿江苏南 Fig. 3 Simulation results of regression model for different area high temperature days in July in Jiangsu (a) northwest of Jiangsu, (b) northeast of Jiangsu, (c) Jianghuai, and (d) Sunan |
利用2008—2009年资料作为独立样本进行试报检验,分别预报了江苏西北部、东北部、江淮地区、沿江苏南四个区域2008—2009年7月份区域平均高温日数,预报情况和实况见表 3,从表 3发现除江苏东北部2008年预报误差较大外,其他区域模型预报效果均较好,长期预报最大误差在3天。且大部分时段预报基本和实况吻合,说明了用海温作为预报因子建立的江苏不同区域高温日数预报模型是可行的,具有较好预报效果。
|
|
表 3 江苏不同区域2008—2010年7月份高温日数试报情况 Table 3 Forecasting results of high temperature days in different area of Jiangsu in July from 2008 to 2010 |
(1) 太平洋海温有两个区域对江苏不同区域平均高温日数具有很好的指示意义,一是赤道附近太平洋中东部区域,对江苏各地的高温日数具有稳定显著的正相关。另一个是西北太平洋区域和东南太平洋区域一般与江苏高温日数存在负相关,因此这些区域的海温变化对江苏高温的长期预报有明显效果。
(2) 江苏不同区域高温日数和太平洋海温相关存在着很大的差异,太平洋海温对沿江苏南地区高温日数有明显的正相关,而对江苏东北部地区则有明显的负相关,对江淮地区和江苏西北部则正负高相关区都存在。赤道附近NINO3和NIND4区海温对江苏不同月份的高温日数以正相关为主,太平洋中北部海温对江苏高温日数则以负相关为主,中部也存在一些正相关。
(3) 经过最优化相关技术处理后,大大增加了因变量和自变量之间的相关度,建立了江苏不同区域夏季逐月平均高温日数预报模型,所建立的预报模型的复相关系数均达到显著水平。
(4) 对建立的高温日数预报模型进行了历史回代和实际预报拟合验证,效果均较好,可以投入业务应用。
| [1] |
朱周平, 钱炳强. 中国东部地区夏季高温南北不均匀分布特征分析[J]. 气象, 2010, 36(11): 26-31. DOI:10.7519/j.issn.1000-0526.2010.11.004 |
| [2] |
连志鸾, 王丽荣. 石家庄高温的天气气候特征及其预报流程[J]. 气象, 2003, 29(10): 17-22. DOI:10.3969/j.issn.1000-0526.2003.10.004 |
| [3] |
邹瑾, 冯晓云, 胡桂芳, 等. 山东省夏季极端高温异常气候变化特征分析[J]. 气象科技, 2004, 32(3): 182-186. |
| [4] |
孙燕, 张秀丽, 唐红昇, 等. 江苏夏季气温异常的时空变化特征[J]. 气象科学, 2009, 29(1): 133-138. |
| [5] |
史印山, 谷永利, 林艳. 京津冀高温天气的时空分布及环流特征分析[J]. 气象, 2009, 35(6): 63-69. DOI:10.7519/j.issn.1000-0526.2009.06.008 |
| [6] |
缪国华, 施丹萍, 唐毅. 夏季多高温年和少高温年的前期环流特征[J]. 气象, 1999, 25(12): 27-32. |
| [7] |
邹燕, 周信禹, 林毅, 等. 福建省夏季高温成因分析[J]. 气象, 2001, 27(9): 35-41. DOI:10.7519/j.issn.1000-0526.2001.09.008 |
| [8] |
张迎新, 张守保. 2009年华北平原大范围持续性高温过程的成因分析[J]. 气象, 2010, 36(10): 8-13. DOI:10.7519/j.issn.1000-0526.2010.10.002 |
| [9] |
贺哲, 李平, 乔春贵, 等. 郑州极端高温天气成因分析[J]. 气象, 2007, 33(3): 68-75. DOI:10.7519/j.issn.1000-0526.2007.03.010 |
| [10] |
赵金彪, 张健挺, 陈丽娜. 夏季多高温年的环流特征及其预测方法探讨[J]. 广西气象, 2004, 25(增刊): 21-25. |
| [11] |
陈丽华, 周率, 党建涛, 等. 2006年盛夏川渝地区高温干旱气候形成的物理机制研究[J]. 气象, 2010, 36(5): 85-91. DOI:10.7519/j.issn.1000-0526.2010.05.012 |
| [12] |
刘梅, 濮梅娟, 高苹, 等. 江苏省夏季最高温度定量预报方法研究[J]. 气象科技, 2008, 36(6): 728-734. |
| [13] |
何卷雄, 丁裕国, 姜爱军. 江苏冬夏极端气温与大气环流及海温场的遥相关[J]. 热带气象学报, 2002, 18(1): 73-82. |
| [14] |
朱定真, 何卷雄, 丁裕国. 江苏地区极端气温振动型态的长期变化特征[J]. 气象科学, 2004, 24(2): 145-153. |
| [15] |
方茸, 杨修群. 中国夏季高温与北极海冰的联系特征[J]. 气象, 2009, 35(3): 81-86. DOI:10.7519/j.issn.1000-0526.2009.03.011 |
| [16] |
朱晓英, 吴志伟. 江苏省夏季气温异常的海气背景[J]. 气象, 2002, 28(5): 32-36. DOI:10.7519/j.issn.1000-0526.2002.05.007 |
| [17] |
管兆勇, 蔡佳熙, 唐卫亚, 等. 长江中下游夏季气温变化型与西太平洋副高活动异常的联系[J]. 气象科学, 2010, 30(5): 666-675. |
| [18] |
刘瑞兰, 徐卫丽, 李国强, 等. ENSO现象对山西省天气气候的影响[J]. 山西师范大学学报(自然科学版), 2009, 23(4): 124-128. |
| [19] |
汤志成, 孙涵. 最优化因子处理及加权多重回归模型[J]. 气象学报, 1992, 5(4): 514-517. DOI:10.11676/qxxb1992.064 |
| [20] |
章基嘉, 葛玲. 中长期天气预报基础[M]. 北京: 气象出版社, 1983: 254-282.
|
 2011, Vol. 37
2011, Vol. 37 