2. 江西省气象科学研究所,南昌 330046;
3. 江西省彭泽县气象局,彭泽 332700
2. Meteorological Science Institute of Jiangxi Province, Nanchang 330046;
3. Pengze Meteorological Station of Jiangxi Province, Pengze 332700
热量资源是重要的农业气候资源,平均气温是衡量热量资源的重要指标,特别是稳定通过0,5,10℃的积温及其初终日等指标,是农业中常用的农业气候资源指标。我国年平均气温大体上呈纬向分布,北低南高[1-2],此外,坡度、坡向、海拔高度等地形因子也对年平均气温的分布起很大作用,一般来讲,随海拔高度增加,年平均气温下降,随海拔高度递减方式有线性、指数递减等[3-5],高大山系多可划分为若干个垂直气候带,其物种分布也有很大差异;坡向对山区气温的分布也起很大作用,在局地北坡气温低于南坡,而东西坡的温度垂直分布方式则比较复杂,与局地气候特点有关。近年来,随着GIS技术、数字高程模型(DEM)和气象卫星遥感技术的发展,使基于细网格的气象要素空间插值物理估算成为可能[6-11]。我国现有将近3000个国家气象站,多处于城郊和地势相对平坦的地方[12],气温是最基本的观测要素之一,光凭气象站的资料,无法准确地反映复杂地形下的气温分布情况,需要将气温要素值外推到无气象资料的地方。本文采用1998—2007年全国651个基本、基准站的1月和7月最高气温进行空间估算试验对各种估算模型进行试验,对估算结果进行误差分析,结合估算结果空间分布的合理性分析,确定最佳的估算模型。采用全国2346个国家气象站1971—2000年的气温观测资料和全国1:25万数字高程模型(DEM)资料,开展实际地形下全国热量资源的估算。本文所用气象资料均由中国气象局国家气象中心提供。
1 热量估算模型 1.1 试验模型选择气温的估算方法非常多,每种方法各有不同的侧重点和优势,各种方法按照物理属性,可以分为以下4大类。一是几何或函数插值方法,包括反距离加权法(IDW)、梯度距离平方反比法(GIDW)、泰森多边形法、曲线拟合等;二是数学模型法,包括线性回归、多项式、样条函数法(Spline)、趋势面分析等;三是随机模拟方法,包括克里格法(Kriging)、目标插值等;四是基于物理过程的模拟方法,主要是大气动力学模型法。对各种估算方法进行技术分析后,选定了反距离加权法(IDW)、梯度距离平方反比法(GIDW)、样条函数法(Spline)、普通克里格法(Ordinary Kriging)、趋势面法共5种方法进行对比试验。
| $ \mathit{Z} = \left[{\sum\limits_{i = 1}^n {\frac{{{Z_i}}}{{d_i^2}}} } \right]/\left[{\sum\limits_{i = 1}^n {\frac{1}{{d_i^2}}} } \right] $ | (1) |
式中,Z为栅格点气象要素估计值,Zi为气象要素在第i个站点的值,di为插值点到第i个站点的距离,n为用于插值的站点数。
(2) 梯度距离平方反比法(GIDW)[8]
| $ Z = \left[{\sum\limits_{i = 1}^n {\frac{{{Z_i} + \left( {X-{X_i}} \right){C_X} + \left( {Y-{Y_i}} \right){C_Y} + \left( {E-{E_i}} \right){C_e}}}{{d_i^2}}} } \right]/\left[{\sum\limits_{i = 1}^n {\frac{1}{{d_i^2}}} } \right] $ | (2) |
式中,Z为待估算的栅格点气象要素值,X和Xi为待估点与气象站点的X轴坐标值(经度),Y和Yi为待估点与气象站点的Y轴坐标值(纬度),E和Ei为待估点与气象站点的海拔高度。CX,CY和Ce为站点气象要素值与X,Y和海拔高程的多元回归系数。di为待估点到第i站点的直线距离,n为用于插值的气象站点的数目。
(3) 样条函数法(Spline)
| $ Z = \sum\limits_{i = 1}^n {{A_i}d_i^2\log {d_i} + a + bx + cy} $ | (3) |
式中,Z为待估算的栅格点气象要素值,di为插值点到第i个气象站点的距离,a+bx+cy为要素的局部趋势函数;x、y为插值点的地理坐标,为一个基础函数,通过它可以获得最小化的曲率,Ai,a,b和c为方程系数,n为用于插值的气象站点的数目。
(4) 普通克里格法(Ordinary Kriging,简称OK法)[14]
地质统计学中的克里格法以区域化变量理论为基础,半变异函数为其分析工具,对空间分布具有随机性与结构性的变量的研究具有其独特的优点。克里格方法中的预测结果将与概率联系在一起,依赖于数学模型和统计模型,引入了包括概率模型在内的统计模型使之不同于确定性插值方法。在地理统计学中,可以计算各观测值之间的距离来反映空间位置信息,也可以用距离的函数来模拟自相关性。待估点x0的气象要素值就是周围范围内n个已知测点xi的变量值Z(xi)的线性组合,其数学表达式为:
| $ Z\left( {{x_0}} \right) = \sum\limits_{i = 1}^n {{\lambda _i}Z\left( {{x_i}} \right)} $ | (4) |
式中,Z(x0)是未知点的值;λi是第i个站点上气象要素值Z(xi)的权重,用来表示各站点要素值对估值Z(x0)的贡献,由克里格方程组计算获得;xi表示站点的位置;n为已知站点个数。
(5) 趋势面方法
通过气象站的地理参数(例如经度、纬度、海拔高度、各方向起伏度等)与气象要素进行逐步回归,获得如下公式:
| $ Z = f\left( {\alpha, \beta, \gamma, \cdots } \right) + \omega $ | (5) |
式中α、β、γ为地理因子,用逐步回归法建立趋势面模型,再利用ω进行小地形残差订正。
1.2 估算误差分析方法(1) 交叉检验法(cross-validation)[15]
即将参与建模的各站依次作为检验站,不参与模型构建,用以比较实际观测值与估算值的差值,以此来判断插值方法的优劣。
(2) 平均绝对误差(MAE)和均方根误差(RMSIE)
| $ MAE = \frac{{\sum\limits_{i = 1}^n {|{\mathit{Z}_{\mathit{a, i}}} - {\mathit{Z}_{\mathit{e, i}}}|} }}{n} $ | (6) |
| $ RMSIE = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{\mathit{Z}_{\mathit{a, i}}} - {\mathit{Z}_{\mathit{e, i}}}} \right)}^2}} }}{n}} $ | (7) |
上两式中Za, i是指要素台站观测值,Ze, i为要素模式估算值,n为站点数。
1.3 各种气温估算模型的比较引入经度、纬度、海拔高度、各方向起伏度、周围25 km2平均海拔高度等共17个因子,各因子均取值于全国1:25万数字高程模型(DEM)资料,用逐步回归法建立趋势面模型,对估算结果进行残差订正。反距离加权法(IDW)、样条空间法(Spline)、普通克里格法(Kriging)采用ARCGIS 9.0的空间分析模块(Spatial Analyst)提供的程序进行气象要素空间估算。梯度距离平方反比法(GIDW)和趋势面法则开发了专门的程序进行估算。采用了交叉分析的方法统计误差。
用上述5种方法,采用1998—2007年全国651个基本、基准站的1月和7月平均气温、平均最高气温进行空间估算试验,估算结果的空间分辨率为0.01°×0.01°,并利用气象站的资料计算各自的平均绝对误差(MAE)和均方根误差(RMSIE)。1月和7月平均气温、平均最高气温用GIDW法估算结果经交叉检验,MAE最小,RMSIE也最小,误差分布均匀;Kriging法的MAE和RMSIE均为最大,其次为Spline法。表 1所列为1月平均气温估算误差分析结果。
|
|
表 1 1998—2007年全国651个基本、基准站1月平均气温插值结果误差(单位:℃) Table 1 The interpolation error analysis of January mean temperature of the 651 basic meteorological stations of China, from 1998 to 2007 (unit:℃) |
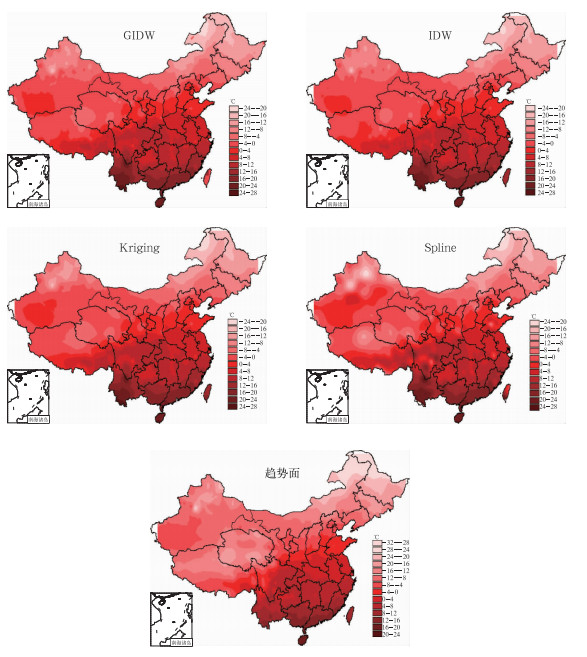
以1月平均气温估算结果为例,从图 1可以看出,5种方法的估算结果总体分布比较一致,Spline法、Kriging法估算的分布图等值线分布平滑,高、低值中心分布自然,用来进行理论分析尚好,但作为气候资源图,其不够精细,未考虑地形、海拔高度的影响,误差较大,不适合热量资源的精细化估算;趋势面法估算的结果比较精细,较好地反映了局地地形的影响,但等值线存在的不连续点,是其主要缺陷;IDW法估算的分布图地形因子影响得到了较好的反映,但存在局地异常高、低值中心,俗称“牛眼”缺陷,局地不连续情况明显;GIDW方法估算的结果与IDW法的较为一致,在5种方法的估算图中其最为精细、连续,很好地反映了局地地形的影响,特别是在海拔高度落差大的地区,海拔对气温的分布影响得到了很好的体现。综合评估结果为,GIDW法用于估算热量资源较好地反映了局地山地地形、海拔高度变化的影响,交叉检验误差最小,误差分布均匀,精细化程度高,该方法最优。
|
图 1 用5种方法估算的全国1998—2007年1月平均气温空间分布图(单位:℃) Fig. 1 The January mean temperature distributions in China calculated by the five methods of China, from 1998 to 2007 (unit:℃) |
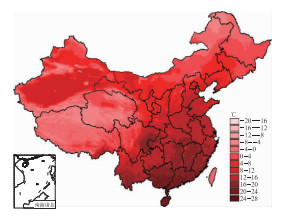
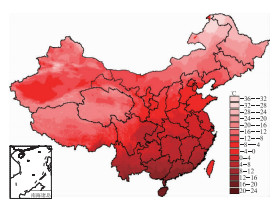
应用GIDW法对全国2346个气象站1971—2000年的年、季、月、旬平均气温要素进行估算,并对估算误差进行统计。由表 2可见,年平均气温、1月平均气温、7月平均气温估算的MAE分别为0.39, 0.57和0.38℃,处于比较低的水平。对比表 1和表 2,可以看出对于GIDW方法来说,采用2346站资料估算结果的MAE, RMSIE均远小于用651个站资料估算的结果,这说明采用相对密集的台站资料估算热量资源可以较大幅度提高估算精度。图 2~4为年平均气温、1月平均气温、7月平均气温估算结果,由图 2~3可见,全国年平均和1月平均气温分布纬向分布较明显,但在新疆塔克拉玛干等沙漠地区,气温存在高值区,明显高于同纬度的其他地区,华南气温最高,东北、青藏高原最低。海拔高度对气温的影响也很明显,青藏高原海拔高度高,其气温值明显低于处于同纬度的我国中东部地区。另外,在横断山脉等地形起伏很大的地区,温度的垂直梯度很大。由图 4可见,全国7月平均气温纬向分布不明显,特别东部地区南北差异小,西部地区则呈北高南低分布,海拔高度对气温分布的影响大。对比图 1和图 3,用GIDW方法估算,采用2346站资料的全国1月气温分布图的精细化程度高于用651站资料估算的分布图,地形影响得到了更为清晰的体现。
|
|
表 2 1971—2000年全国2346年气象站年平均气温、1月平均气温、7月平均气温估算结果交叉验证误差(单位:℃) Table 2 Cross-validation error analysis of estimation results of annual mean temperature, January mean temperature, and July mean temperature of the 2346 meteorological observation stations of China, from 1971 to 2000 (unit: ℃) |
|
图 2 1971—2000年实际地形下全国年平均气温空间分布图(单位:℃) Fig. 2 The spatial distribution of annual mean temperature based on the actual terrain of China, from 1971 to 2000 (unit:℃) |
|
图 3 1971—2000年实际地形下全国1月平均气温空间分布图(单位:℃) Fig. 3 The spatial distribution of January mean temperature based on the actual terrain of China, from 1971 to 2000 (unit:℃) |
|
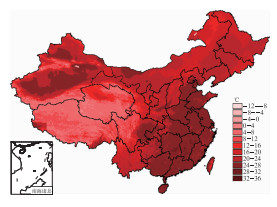
图 4 1971—2000年实际地形下全国7月平均气温空间分布图(单位:℃) Fig. 4 The spatial distribution of July mean temperature based on the actual terrain of China, from 1971 to 2000 (unit:℃) |
应用GIDW法对全国2346个气象站1971—2000年的0, 5, 10, 12和15℃初日序日Dn进行了估算和误差分析,序日Dn是指以每年1月1日为起始日的日期序号,1月1日的Dn为1,以后依次加1,12月31日为365或366(闰年)。估算结果见图 5,由图可见,各级界限温度初日序日东部纬向分布明显,南小北大,地形影响不明显;而西部地形复杂,海拔高度因子起决定性作用,0和5℃初日青藏高原为高值区,而新疆塔克拉玛干沙漠一带为低值区,其值与中东部地区相当;青藏高原10, 12和15℃初日存在低值中心区,而且随着界限温度的升高,低值中心区域的面积呈增大趋势,同时高原边缘由于海拔高度非常高,为高值区,初日序日的水平梯度大。表 3所示的各界限温度初日序日的估算结果的MAE均在8 d以下,平均相对误差小于5%。
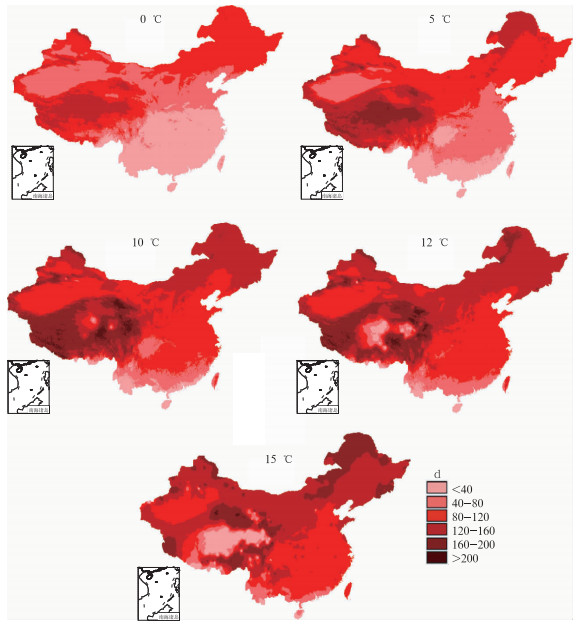
|
图 5 1971—2000年实际地形下全国各界限温度初日序日分布图(单位:d) Fig. 5 The spatial distributions of starting day of each limit temperature based on the actual terrain of China, from 1971 to 2000 (unit: d) |
|
|
表 3 1971—2000年全国2346个气象站各界限温度初日估算结果交叉验证误差(单位:d) Table 3 Cross-validation error analysis of estimation results of the starting day of each limit temperature of the 2346 meteorological observation stations of China, from 1971 to 2000 (unit:d) |
应用GIDW法对全国2346个气象站1971—2000年的0, 5, 10, 12和15℃终日进行了估算和误差分析,由图 6可见,各级界限温度终日序日东部纬向分布明显,南大北小;西部地形复杂,海拔高度因子起决定性作用,青藏高原为终日低值区,而新疆塔克拉玛干沙漠一带为高值区;东部地区0和5℃终日差别小,局地地形影响不明显,而10, 12和15℃终日分布则对海拔高度差异很敏感,局地地形对于终日的分布有非常明显的影响,特别是横断山脉附近局地海拔高度差异大,其终日序日的水平梯度大,10℃终日尤为明显。另外,表 4所示的各界限温度初日的估算结果的MAE均在8 d以下,平均相对误差小于5%。
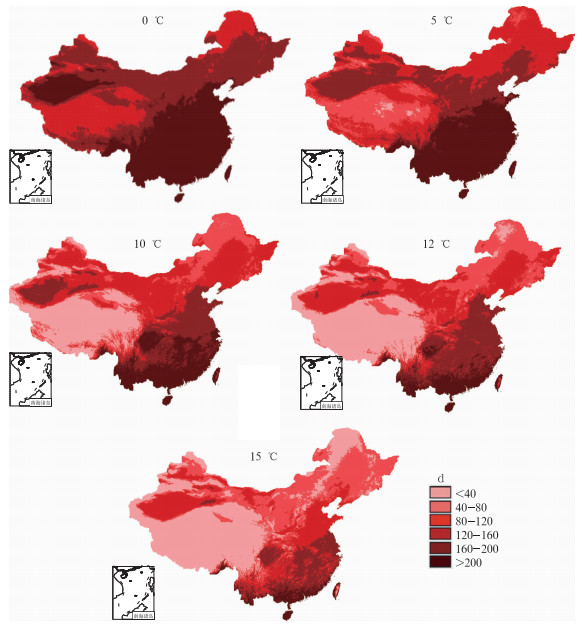
|
图 6 1971—2000年全国各界限温度终日序日分布图(单位:d) Fig. 6 The spatial distributions of ending day of each limit temperature based on the actual terrain of China, from 1971 to 2000 (unit: d) |
|
|
表 4 1971—2000年全国2346个气象站各界限温度终日估算结果交叉验证误差(单位:d) Table 4 Cross-validation error analysis of estimation results of the ending day of each limit temperature of the 2346 meteorological observation stations of China, from 1971 to 2000 (unit: d) |
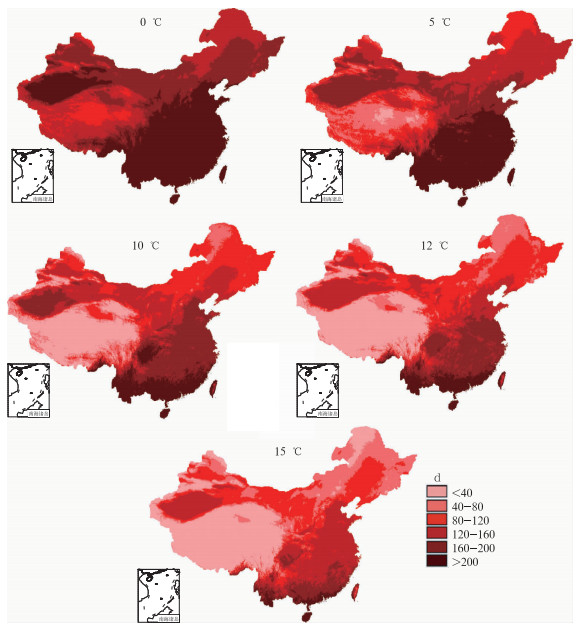
应用GIDW法对全国2346个气象站1971—2000年的0,5,10,12和15℃间隔天数进行了估算和误差分析,由图 7所示的估算结果可见,各级界限温度间隔天数与前述初、终日序日的分布类似,东部纬向分布明显,西部受海拔高度影响大;局地海拔高度变化引起的变化情况得到了很好的体现,山区的各级界限温度间隔天数垂直差异明显;青藏高原的各级界限温度间隔天数最小。另外,从表 5可见,各级界限温度间隔天数的MAE均在6 d以下,平均相对误差不超过5%。
|
图 7 1971—2000年实际地形下全国各界限温度积温天数分布图(单位:d) Fig. 7 The spatial distributions of the accumulated temperature days days of each limit temperature based on the actual terrain of China, from 1971 to 2000 (unit: d) |
|
|
表 5 1971—2000年全国2346个气象站各界限温度间隔天数估算结果交叉验证误差(单位:d) Table 5 Cross-validation error analysis of estimation results of the accumulated temperature days of each limit temperature of the 2346 meteorological observation stations of China, from 1971 to 2000 (unit: d) |
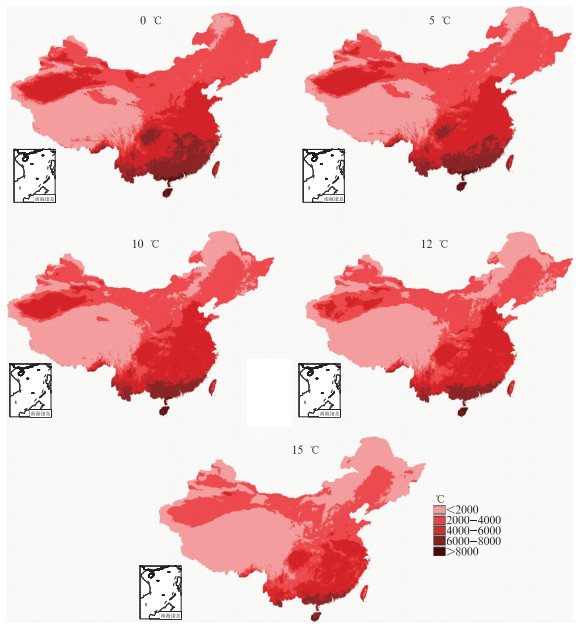
应用GIDW法对全国2346个气象站1971—2000年的0,5,10,12和15℃积温进行了估算和误差分析,估算结果见图 8。由图可见,我国各界限温度积温的分布基本上呈纬向分布,北低南高,华南地区热量资源最为丰富,其次为中东部地区,东北、青藏高原热量资源最少。热量资源受海拔高度等地形因子影响大,垂直分布明显,在山区存在明显的气候垂直分区,特别是在横断山脉、秦岭等地区,存在很大的热量资源垂直梯度。误差分析的结果见表 6,MAE均在150℃以下,相对误差不超过5%,精度较高。
|
图 8 1971—2000年实际地形下全国各界限温度下的积温分布图(单位:℃) Fig. 8 The spatial distributions of the accumulated temperature of each limit temperature based on the actual terrain of China, from 1971 to 2000 (unit:℃) |
|
|
表 6 1971—2000年全国2346个气象站各界限温度积温估算结果交叉验证误差(单位:℃) Table 6 Cross-validation error analysis of estimation results of the accumulated temperature of each limit temperature of the 2346 meteorological observation stations of China, from 1971 to 2000 (unit: ℃) |
(1) 我国热量资源分布主要受纬度、海拔高度等因子影响,通过对IDW,GIDW,Spline,Kriging和趋势面5种方法的估算试验和交叉检验,结果表明Spline和Kriging法未考虑海拔高度等地形因子,估算结果比较宏观,反映的是要素平面上的分布情况,虽然空间分布连续自然,但不适合热量资源的精细化估算。IDW,GIDW和趋势面法均考虑了海拔高度等自然地理因子,基于数字高程模型(DEM),可实现精细化估算。
(2) IDW,GIDW和趋势面法3种方法中,趋势面法的结果比较精细,较好地反映了局地地形的影响,但等值线存在的不连续点,是其主要缺陷。IDW法的分布图地形因子影响得到了较好的反映,但存在局地异常高、低值中心,俗称“牛眼”缺陷,局地不连续情况明显。GIDW法综合考虑了气象要素场的水平空间分布和垂直分布,较好地反映了局地地形对热量资源影响,较为准确地反映了垂直气候带分布情况,空间分布连续,且估算误差最小,较适合热量资源的精细化估算。
(3) 对于GIDW方法来说,采用2346站资料估算结果的MAE,RMSIE均远小于用651个站资料估算的结果,用2346站资料的全国1月气温分布图的精细化程度高于用651站资料估算的分布图,采用相对密集的台站资料估算热量资源可以较大幅度提高估算精度。
(4) 我国热量资源的分布水平面基本上呈纬向分布,北低南高,华南地区热量资源最为丰富,其次为中东部地区,东北、青藏高原热量资源最少。热量资源受海拔高度等地形因子影响大,垂直分布明显,在山区存在明显的气候垂直分区。
| [1] |
竺可桢, 卢鋈. 中国气候之要素(续)[J]. 地理学报, 1935, 2(2): 1-2. |
| [2] |
《中华人民共和国气候图集》编委会. 中华人民共和国气候图集[M]. 北京: 气象出版社, 2002: 16-28.
|
| [3] |
傅抱璞. 起伏地形中的小气候特点[J]. 地理学报, 1963, 29(3): 175-187. |
| [4] |
傅抱璞. 坡地方位对小气候的影响[J]. 气象学报, 1962, 32(1): 71-86. DOI:10.11676/qxxb1962.007 |
| [5] |
翁笃鸣, 孙治安. 我国山地气温直减率的初步研究[J]. 地理研究, 1982, 3(2): 24-34. |
| [6] |
汪学兵, 柳玲, 吴中福. 空间内插方法在GIS中的应用[J]. 重庆建筑大学学报, 2004, 26(1): 35-39. |
| [7] |
吴焕萍. GIS技术在气象领域中的应用[J]. 气象, 2010, 36(3): 90-100. DOI:10.7519/j.issn.1000-0526.2010.03.013 |
| [8] |
林忠辉, 莫兴国, 李宏轩, 等. 中国陆地区域气象要素的空间插值[J]. 地理学报, 2002, 57(1): 47-56. DOI:10.11821/xb200201006 |
| [9] |
袁爱民, 王建源. 气候要素栅格化技术方法研究[J]. 气象, 2006, 32(6): 111-115. DOI:10.7519/j.issn.1000-0526.2006.06.020 |
| [10] |
孙和平, 罗少聪. 中国及其邻区地表气象数据预处理和网格化数值结果分析[J]. 地壳变形与地震, 1998, 18(3): 51-56. |
| [11] |
侯英雨, 张佳华, 延昊, 等. 利用卫星遥感资料估算区域尺度空气温度[J]. 气象, 2010, 36(4): 75-79. DOI:10.7519/j.issn.1000-0526.2010.04.013 |
| [12] |
中国气象局. 地面气象观测规范[M]. 北京: 气象出版社, 2003: 23-24.
|
| [13] |
蔡秀华, 曹鸿兴. 资料插值的进展[J]. 气象, 2008, 31(8): 4-7. |
| [14] |
徐建华. 现代地理学中的数学方法[M]. 第二版. 北京: 高等教育出版社, 2002.
|
| [15] |
Holdway M R. Spatial modeling and interpolation of monthly temperpolation using kriging[J]. Clim Res, 1996, 24: 1835-1845. |
 2011, Vol. 37
2011, Vol. 37