2. 中国气象局综合观测司, 北京 100081;
3. 北京市气象台,北京 100086
2. Department of Integrated Observations, CMA, Beijing 100081;
3. Beijing Meteorological Observatory, Beijing 100086
在气象服务中,高空风是非常重要的气象观测量。我国自20世纪50年代起,与国际同步实施了世界天气监测 (WWW) 计划,建立了包含120个探空站的高空探测网,1998年开始,为了提高探测设备的自动化水平,提高高空探测精度,中国气象局对高空气象装备进行了升级换代,以南京大桥机械厂研制的L波段探空系统替代老的59-701探空系统,目前已经有90套L波段探空系统投入业务使用,未来计划全部采用L波段探空系统。李伟等对59-701探空系统与L波段探空系统进行了对比,同时利用国家气象中心数值预报系统6小时初估场对L波段电子探空仪探测数据进行了评估,结果表明,L波段电子探空仪与59-701探空系统保持了数据的一致性,离散性减小,测量更加准确[1]。
气象观测具有准确性、代表性与可比较性三个特点,世界气象组织认为影响观测数据质量的因素多种多样,包括观测环境、观测仪器、观测方法、业务规程等[2-3]。对于现行业务L波段探空系统,温度、湿度与气压观测精度主要取决于传感器,而风的观测精度影响量除了地面雷达测角误差、测距误差外,还与计算方法有关。现行业务L波段探空系统中采用的是1分钟间隔的气球坐标计算的风,即取该整分钟及其上下各两秒的仰角或方位角或斜距数据之和的平均值,代表该分钟风值。如果在1分钟的时间内风向发生变化,这种计算方法所得结果不能完全代表风的实际情况。与RS92探空系统的每秒间隔的GPS测风数据相比,业务L波段探空系统给出的每分钟间隔数据过于平滑,并且,在业务L波段探空系统中利用测风数据计算量得风层的时间间隔又规定为:前21分钟以1分钟为间隔,22~42分钟以2分钟为间隔,43分钟及以后以4分钟为间隔。这仍是以两点计算的风。实际上每秒钟L波段探空系统就测得一组斜距、方位和仰角数据,分钟风的计算方式没有利用所有的探测结果,不能完全发挥新型探测装备的效益。贺宏兵等提出了采用小波变换计算层风的新方法来计算高空风,以适应高时空分辨率的探空设备发展[4]。邱传涛等对常用的平均风向计算方法进行了比较,结果显示计算方法的不同会引起较大的误差[5]。张玉存等认为在多种平均方法中,矢量平均方法具有明显的优越性[6]。
下面在比较业务分钟风与秒数据滑动平均风两种计算方法的基础上,就未来高空风计算方法的改进提出建议。
1 计算方法分析L波段探空系统采用测角测距方式进行测风,利用斜距与仰角得到水平投影,再利用水平投影与方位角进行极坐标与直角坐标转换,进而利用时间位移差计算高空风。
1.1 目前业务上所用计算方法以R代表地面雷达测得的斜距,L代表斜距的水平投影,t代表雷达测得的时间,δ代表雷达测得的仰角,α代表雷达测得的方位角,i与i+1代表参与计算的两个相邻位置。
| $\begin{array}{*{20}{c}} {{L_i} = {R_i}\cos {\delta _i}}&{{L_{i + 1}} = {R_{i + 1}}\cos {\delta _{i + 1}}} \end{array}$ | (1) |
| $\begin{array}{*{20}{c}} {{x_i} = {L_i}\cos {\alpha _i}}&{{x_{i + 1}} = {L_{i + 1}}\cos {\alpha _{i + 1}}} \end{array}$ | (2) |
| $\begin{array}{*{20}{c}} {{y_i} = {L_i}\sin {\alpha _i}}&{{y_{i + 1}} = {L_{i + 1}}\sin {\alpha _{i + 1}}} \end{array}$ | (3) |
| $\Delta x = {x_{i + 1}} - {x_i}$ | (4) |
| $\Delta y = {y_{i + 1}} - {y_i}$ | (5) |
| $\Delta t = {t_{i + 1}} - {t_i}$ | (6) |
风速:
| $V = \frac{1}{{\Delta t \times 60}}\sqrt {\Delta {x^2} + \Delta {y^2}} $ | (7) |
风向:
| $\theta = \arctan (\Delta y/\Delta x)$ | (8) |
| $\Delta x > 0,D = 180°+ \theta $ | (9) |
| $\Delta x < 0,\Delta y \ge 0:D = 360°+ \theta $ | (10) |
| $\Delta y < 0,D = \theta $ | (11) |
| $\Delta x = 0,\Delta y = 0:D = 静风(C)$ | (12) |
| $\Delta y > 0:D = 270°$ | (13) |
| $\Delta y < 0:D = 90°$ | (14) |
根据以上公式,可以计算出每秒钟的风向与风速。但是在业务处理中,由于秒数据风脉动太大,因此实际上计算的是分钟风,取整分钟前后两秒共5个斜距、仰角、方位角进行平均计算。这里5点平均的假设条件应是5次采样的方位、仰角、斜距都呈线性均匀变化,计算的平均值正好等于整分钟的测量值。如果整分钟数据很少错误,取5点平均没有必要;如果整分钟的数据错误,其他4点数据正确,取平均值可以减小整分钟值的误差;如果整分钟数据正确,其他4点数据有错误,取平均值反而会增加整分钟数据的误差。另外,以分钟为时间间隔计算风虽然消除了这段时间内由于探空仪的摆动和雷达的定位误差引起的脉动,但也消除了大气的真实脉动。气象学上为了取得有比较性的数据,要把脉动去除,包括风本身的脉动[7]。多长时间和多大的脉动应该被去除是值得研究的问题。目前气象业务采用的方法,其原理还是基于59-701雷达设备原理上,59-701雷达测量的角坐标数据,只能是1分钟1次,无法平滑,且测量精度也比L波段雷达低[8]。目前业务已经换型为L波段雷达,设备变了,计算方法也应该相应改变。
1.2 秒数据滑动平均风计算方法上面提到,每秒钟L波段探空系统就能测得一组斜距、方位和仰角数据,进而计算得到每秒的风速风向值,而秒数据风多长时间和多大的脉动应该被去除 (即得到平滑) 是值得研究的问题。由于风是一个矢量,因此采用矢量的滑动平均法来探讨高空风的平滑计算。
首先利用每秒探测得到的斜距、仰角、方位角,按照公式 (4)~(6),计算每秒风的南北分量u与东西分量v:
| $u = \Delta x/\Delta t$ | (15) |
| $v = \Delta y/\Delta t$ | (16) |
这里Δt=1秒。
滑动平均法是将规定时段 (窗口) 内的每秒风速分量,先用代数法对相同分量进行平均求出两个平均值
| $\overline u = \sum\limits_{i = 1}^n {{u_i}} /n$ | (17) |
| $\overline v = \sum\limits_{i = 1}^n {{v_i}} /n$ | (18) |
这里n是规定时段内秒的个数。合成后的风速:
| $V=\sqrt{{{{\bar{u}}}^{2}}+{{{\bar{v}}}^{2}}} $ | (19) |
合成后的风向:
| $D = \arctan (\overline v /\overline u )$ | (20) |
根据u和v的正负,参照公式 (8)~(14) 判断其所处的象限,计算出实际的风向。
利用上述方法计算得到的风速风向代表窗口中间时刻的风速风向,然后去除窗口第1秒的数据,加入窗口结束后下1秒的数据进行重复计算,即窗口向下1秒移动并求平均,这样就可以得到风速风向1秒间隔的连续变化曲线。用这种方法得到的风速风向包含了该时段内的所有样本。由于计算得到的风速风向起始时间为窗口的中间时刻,而在这一时刻之前的数据可与地面风速风向仪的数据进行内插处理获得,最终得到从地面直至球炸的每秒连续数据。
下面通过实例数据分析,将计算结果与Vaisala公司GPS RS92探空仪的秒数据风、现行业务L波段分钟风进行比较,最终选取合适的窗口。
2 计算结果比对 2.1 比对实验和误差计算方法在锡林浩特和阳江两个探空站分别做过两次比对实验,均采用探空仪同球施放方法,即在一个探空气球上同时悬挂一个L波段电子探空仪与两个RS92探空仪。首先根据同球双施放原则[9]计算RS92探空仪的动态测量误差,即传感器相同的两探空仪,以批统计方法得到的两者各自的标准差应近似相等。因此利用两个RS92探空仪之间相对差值的标准偏差s可计算出RS92探空仪自身的动态测量误差sR:
| ${s_R} = s/\sqrt 2 $ | (21) |
然后将RS92探空仪作为参考标准,根据L波段探空仪与RS92探空仪的同球施放数据计算两者之间的标准偏差sD和系统偏差,再利用公式 (22) 计算出L波段电子探空仪的动态测量误差sL:
| ${s_L} = \sqrt {s_D^2 - s_R^2} $ | (22) |
将现行业务用高空风计算方法和秒数据滑动平均风计算方法分别得出的风速风向值与GPS测风进行比较并计算批统计误差,从而找出合适的高空风平滑算法。
锡林浩特站的比对时段为2008年6月21—28日,有27次探空数据,阳江站为同年的7月13—16日,有13次探空数据,一共40次探空数据作批统计处理,结果应具有代表性。
2.2 比对结果分析 2.2.1 测风数据全过程分析根据以上公式分别计算4分钟、2分钟、1分钟、30秒和10秒钟的滑动平均风以及业务分钟风,并与GPS测风相比较。其结果如下。
图 1和图 2分别是锡林浩特站和阳江站比对结果的典型例子。现行业务L波段系统计算所得的风速风向值为分钟数据,因此图中的各组数据是以整分钟进行比较。从图中可以看出,和GPS测风数据相比,10秒滑动平均风的曲线波动明显,而现行业务分钟风和4分钟滑动平均风的曲线过于平滑,2分钟滑动平均风则在43分钟后曲线平滑明显,只有30秒滑动平均风和1分钟滑动平均风的曲线与GPS测风曲线吻合得较好。
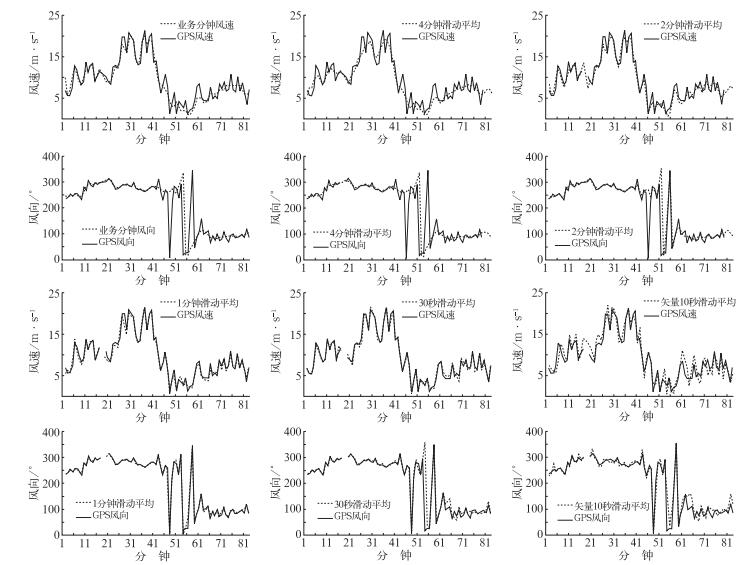
|
图 1 2008年6月21日锡林浩特滑动平均风、业务分钟风与GPS测风比较 Fig. 1 Comparison of the moving average wind and the operational minute wind with GPS measuring wind at Xilinhot Upper-Air Station on 21 June 2008 |

|
图 2 2008年7月15日阳江滑动平均风、业务分钟风与GPS测风比较 Fig. 2 Comparison of the moving average wind and the operational minute wind with GPS measuring wind at Yangjiang Upper-Air Station on 15 July 2008 |
此外,还分别对各种平滑算法进行了误差统计分析,滑动平均法以秒数据统计。从表 1的系统偏差统计结果看,业务分钟风、滑动平均风和RS92风速风向值的系统偏差均较小,具有可比较性。而从标准差的统计结果得知,4分钟、10秒滑动平均风和业务分钟风风速风向值的标准差较大;2分钟滑动平均风风速风向值的标准差也较大;30秒滑动平均风和1分钟滑动平均风风速风向值的标准差较接近,1分钟滑动平均风的风向标准差还略小于30秒滑动平均风的风向标准差。
|
|
表 1 全过程风速风向统计结果比较 Table 1 Statistical results of the whole process of wind speed and direction |
现行业务中22~42分钟和43分钟之后,分别采用2分钟、4分钟间隔计算平均风,表 2至表 4依据上述时段给出了统计结果。经统计,如图 1、2所示,与业务分钟风的标准差相比较,锡林浩特站高空风在43分钟后有一段风速小且风向急剧变化的区间,导致滑动平均风43分钟后的风向标准差略有增加;而阳江站高空风自22分钟以后风向基本小于100°且变化趋于平缓,使得滑动平均风的风向标准差明显减小;43分钟后两站的30秒和1分钟滑动平均风的风速风向标准差均只有4分钟滑动平均风和业务分钟风风速风向标准差的1/2倍;2分钟滑动平均风风速风向标准差从两站统计结果来看,仍略大于1分钟滑动平均风风速风向标准差。
|
|
表 2 前21分钟风速风向统计结果比较 Table 2 Statistical results of wind speed and direction in the first 21 minutes |
|
|
表 3 22~42分钟风速风向统计结果比较 Table 3 Statistical results of wind speed and direction from the 22nd to 42nd minute |
|
|
表 4 43分钟至球炸风速风向统计结果比较 Table 4 Statistical results of wind speed and direction after the 43rd minute |
锡林浩特站的小风 (风速≤5 m·s-1) 整分钟数据样本有570个,而阳江站的小风整分钟数据样本只有138个。从表 5的统计结果看,小风的风向标准差均有所增加,但30秒和1分钟滑动平均风的风向风速标准差还是明显小于业务分钟风的风向风速标准差,同时比2分钟滑动平均风的结果要好。
|
|
表 5 小风统计结果比较 Table 5 Statistical results of low winds |
L波段雷达测角数据受多路传播影响发生起伏,仰角越低、距离越远,计算出的风向、风速来回摆动越大[10],这里对低仰角、远距离的情况也做了统计分析。图 3为2008年6月22日01:00锡林浩特站的低仰角、远距离、小风速时的放球记录,这段记录的最大仰角为22.05°,最低仰角为12.7°,斜距为70 km。由于阳江站低仰角、远距离、小风速的分钟样本很少,无法做统计分析,锡林浩特站的样本只有192个,且两站均没有仰角在6°左右的数据,因此无法对6°附近的低仰角进行统计分析。从表 6的统计结果看,仍然是1分钟和30秒的滑动平均风风速风向标准差较小。
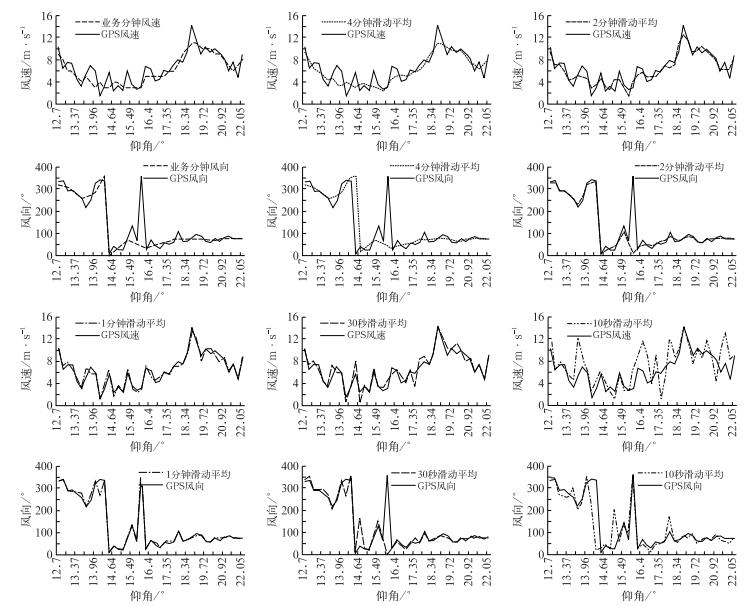
|
图 3 2008年6月22日01时锡林浩特低仰角、远距离、小风速时的测风比较 Fig. 3 Comparison of the mesuring winds under the circumstance of low elevation, long-distance and low winds at 01:00 BT 22 June 2008 at Xilinhot Upper-Air Station |
|
|
表 6 低仰角、远距离、小风速统计结果比较 Table 6 Statistical results of long-distance, low elevation and low winds |
根据上述分析可以得到以下初步结论:
(1) 和现行业务L波段探空系统只利用5点坐标数据获得的分钟风相比较,滑动平均风计算方法能在充分利用全部探空坐标数据, 在适当选取移动平均窗口的基础上,获得与GPS测风系统较一致的风速风向测量结果;
(2) 现行业务L波段探空系统对风的脉动平滑较大,一些反映风速风向快速变化的真实结果也被平滑了,而滑动平均法能在探空系统现有测量精度的前提下,通过计算方法较好地消除脉动影响;
(3) 通过滑动平均法的秒数据统计结果可以看出,滑动平均窗口的选取在30秒以上为宜,若采用1分钟滑动平均窗口计算每秒钟高空风,在整体趋势上与GPS测风一致性最好。
建议未来业务L波段探空系统中风的计算方法改进时,采用滑动平均计算每秒钟高空风,替代现行5点坐标平均计算整分钟高空风的方法。此外,根据现行《常规高空探测规范》规定的测风数据20分钟以上采用2分钟和4分钟间隔计算平均风,是由于原59-701探空雷达对远距离、低仰角目标以及高空风小时测量和计算误差较大,为得到较为准确的数值而采取的措施,这种方法掩盖了800 m以致1600 m厚度的风速风向变化。在采用L波段探空雷达的情况下,由于测角和测距都要比701雷达准确得多,缩小时间间隔以反映风的实际变化,是必要和可行的。而且通过高空小风数据和低仰角、远距离风的统计分析得知,滑动平均法对于减小高空风数据动态误差具有明显优势,因此,可以在空中风探测的整个过程都采用1分钟滑动平均法,也可以前20分钟采用30秒滑动平均,以后采用1分钟滑动平均的分段平均方法。
目前,中国气象局正在组织国产GPS探空仪的考核,建议可以采用滑动平均法来继续探讨GPS测风系统的滑动平均窗口选取,且验证RS92测风数据的计算方法是否也采用的是滑动平均法。
另外,这项工作也给出一个启迪,在误差分析方面,不仅要注重硬件分析,软件算法引起的误差也不可忽视。
| [1] |
李伟, 李书严, 陶士伟, 等. L波段高空气象探测系统性能评估[J]. 仪器仪表学报, 2008, 29(4): 732-735. |
| [2] |
WMO. Guide to Meteorological Instruments and Methods of Observation (V7.0), Geneva, 2006.
|
| [3] |
张文建. 世界气象组织综合观测系统 (WIGOS)[J]. 气象, 2010, 36(3): 1-8. DOI:10.7519/j.issn.1000-0526.2010.03.001 |
| [4] |
贺宏兵, 章建军. 基于小波变换的高空风估计[J]. 解放军理工大学学报:自然科学版, 2002, 3(2): 81-84. |
| [5] |
邱传涛, 李丁华. 平均风向的计算方法及其比较[J]. 高原气象, 1997, 16(1): 94-98. |
| [6] |
张玉存, 宋呈文. 采用矢量法计算风速风向平均值[J]. 气象仪器装备, 2004(2): 1-4. |
| [7] |
黄炳勋. 国内外常规高空观测技术发展近况综述[J]. 气象, 1994, 20(5): P3-9. |
| [8] |
张玉存, 赵炜. 用矢量平均法计算空中风连续变量的方法[J]. 军事气象水文, 2006(5): 7-11. |
| [9] |
中华人民共和国国家军用标准GJB 570. 3A-2008, 2008: 13-14.
|
| [10] |
宋连春, 李伟. 综合气象观测系统的发展[J]. 气象, 2008, 34(3): 3-9. DOI:10.7519/j.issn.1000-0526.2008.03.001 |
 2011, Vol. 37
2011, Vol. 37 