锋面滑升运动是锋面降水的重要原因,预报锋面降水时必须分析锋面滑升运动。因此,有必要弄清是什么原因产生了锋面滑升运动。在教科书中,有锋面滑升运动形成的垂直速度公式[2-3],但该式不能揭示产生锋面滑升运动的物理因子,对锋面滑升运动的成因尚缺少理性的、系统的认识,其他常见对锋面滑升运动物理过程的描述也显露出表面性、片面性、主观臆想性。因而,从理论上弄清锋面滑升运动的物理机制是非常必要的。要弄清锋面滑升运动的物理机制,首先需要求得锋面坡度公式。已知的锋面坡度公式是温度为间断面的锋面坡度公式[2-3],即马古拉斯公式。该式过分简化,不能揭示锋面滑升运动的物理机制。本文通过建立模型(图 1)依据大气动力学原理[1],经过数学演绎,推导得出温度为连续函数的锋面坡度公式(马古拉斯公式是其特例)。在该式的基础上,进一步推演出锋面滑升运动与锋面坡度、锋面强度及温度平流间的关系。由大气动力学方程又推导出了锋面滑升运动与风场的关系。应用上述结果,解释了锋面滑升运动与天气形势的关系。从而解决了如何分析锋面滑升运动的问题,明确了应该分析什么和怎样去分析。
|
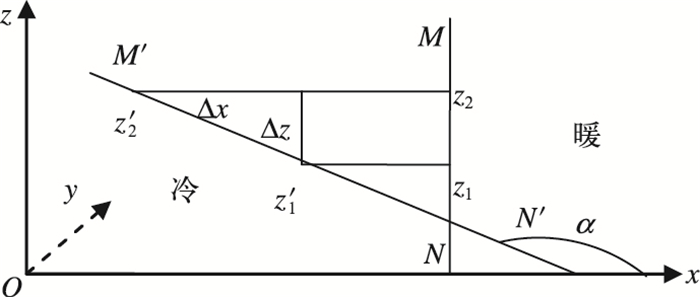
图 1 锋面坡度示意图 Fig. 1 Sketch map of the frontal slope |
如图 1,假定初始时刻锋面MN与地面是垂直的,在水平气压梯度力的作用下,锋面MN倾斜至M′N′,达地转平衡,锋面坡度为
| $ {\rm{tg}}\alpha = \frac{{\Delta z}}{{\Delta x}}{\rm{ }}\left( {\Delta x < 0} \right) $ | (1) |
令c1, c2分别为z1, z2高度上锋面的水平位移速度,则
| $ \Delta x = \int\limits_0^t {\left( {{c_2} - {c_1}} \right){\rm{d}}t} $ | (2) |
| $ w = \left( {u - c} \right){\rm{tg}}\alpha $ |
假定z1, z2高度锋面上的气块沿锋面的滑升速度相等,则
| $ \begin{array}{l} {u_1} - {c_1} = {u_2} - {c_2}\\ {c_2} - {c_1} = {u_2} - {u_1} \end{array} $ |
代入式(2),则
| $ \Delta x = \int\limits_0^t {\left( {{u_2} - {u_1}} \right){\rm{d}}t} $ | (3) |
将自由大气的运动方程[1]代入式(3),有
| $ \Delta x = \int\limits_0^t {\left( {{u_{g2}} - {u_{g1}}} \right){\rm{d}}t} - \frac{1}{f}\int\limits_0^t {\left( {\frac{{{\rm{d}}{v_2}}}{{{\rm{d}}t}} - \frac{{{\rm{d}}{v_1}}}{{{\rm{d}}t}}} \right){\rm{d}}t} $ | (4) |
由于y方向与锋面平行,可认为
| $ \begin{align} \Delta x =& \int\limits_0^t {\left( {{u_{g2}} - {u_{g1}}} \right){\rm{d}}t} - \frac{1}{f}[ \int\limits_0^t {\left( {\frac{{\partial {v_2}}}{{\partial t}} + {u_2}\frac{{\partial {v_2}}}{{\partial x}}} \right)\partial t} -\\ &\int\limits_0^t {\left( {\frac{{\partial {v_1}}}{{\partial t}} + {u_1}\frac{{\partial {v_1}}}{{\partial x}}} \right){\rm{d}}t} ] \end{align} $ | (5) |
由于锋面为物质面[2-3],即锋面上的气块不离开锋面,并假定初始时刻风不随高度改变,则
| $ \begin{array}{l} \Delta x = \int\limits_0^t {\left( {{u_{g2}} - {u_{g1}}} \right){\rm{d}}t} - \frac{1}{f}{\rm{ }}\left[ {v\left( {{{z'}_2}} \right) - v\left( {{{z'}_1}} \right)} \right]\\ \Delta x = \int\limits_0^t {\left( {{u_{g2}} - {u_{g1}}} \right){\rm{d}}t} - \frac{1}{f}{\rm{ }}\left( {\frac{{\partial v}}{{\partial x}}\Delta x + \frac{{\partial v}}{{\partial z}}\Delta z} \right)\\ \Delta x = \int\limits_0^t {\left( {{u_{g2}} - {u_{g1}}} \right){\rm{d}}t} - \frac{1}{f}(\frac{{\partial v}}{{\partial x}}\Delta x + {\rm{ }}\frac{g}{{fT}}\frac{{\partial T}}{{\partial x}}\Delta z) \end{array} $ |
上式两边同除Δx,整理得
| $ {\rm{tg}}\alpha = - \frac{{fT}}{{g\frac{{\partial T}}{{\partial x}}}}\left[ {f + \frac{{\partial v}}{{\partial x}} - \frac{f}{{\Delta x}}\int\limits_0^t {\left( {{u_{g2}} - {u_{g1}}} \right){\rm{d}}t} } \right] $ | (6) |
式(6)即为普遍意义的锋面坡度公式,当锋区宽度无限变窄而趋于零时,对式(6)取极限,即得马古拉斯锋面坡度公式。
用实际资料,按式(6)计算出的锋面坡度之值与实际的锋面坡度的大小非常吻合。式中括号内第三项较前两项小得多。
2 锋面滑升运动的物理机制 2.1 锋面滑升运动与锋面特征的关系| $ w = \left[ {{u_{\rm w}} - c} \right]{\rm{tg}}\alpha $ |
冷锋的移速略小于uc[2],则暖空气沿锋面向上滑的必要条件是uc>uw,即锋区有
| $ \frac{g}{{fT}}\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\rm{tg}}\alpha \cdot\frac{{\partial T}}{{\partial x}}} \right) = - \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {f + \frac{{\partial v}}{{\partial x}}} \right) + {\rm{ }}f\frac{{\partial {u_g}}}{{\partial x}} $ | (7) |
将x方向的运动方程取对y的偏导数,略去小项,并注意
| $ \frac{{\partial {u_g}}}{{\partial x}} = \frac{1}{f}\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial u}}{{\partial y}}} \right) - \frac{{\partial v}}{{\partial y}} $ |
将上式代入式(7),得
| $ \frac{g}{{fT}}\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\rm{tg}}\alpha \cdot\frac{{\partial T}}{{\partial x}}} \right) = - \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {f + \frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial y}}} \right) - {\rm{ }}f\frac{{\partial v}}{{\partial y}} $ |
将简化的涡度方程[3]代入上式,得
| $ \begin{align} \frac{{\partial u}}{{\partial x}} =& \frac{g}{{{f^2}T}}\frac{{\partial T}}{{\partial x}}\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\rm{tg}}\alpha } \right) + \\ &\frac{g}{{{f^2}T}}{\rm{tg}}\alpha \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial T}}{{\partial x}}} \right) + \frac{1}{T}\frac{{\partial T}}{{\partial x}}{u_g} \end{align} $ | (8) |
式(8)即为分析锋面滑升运动的公式。由式(8)得:
(1) 当锋面坡度随时间增大时,暖空气上滑,坡度变化越快,锋区等温线越密集,纬度越低,滑升越强;反之下滑。
(2) 当锋区水平温度梯度随时间增大即锋生时,暖空气上滑,水平温度梯度增大越快,锋面坡度越大,纬度越低,滑升越强;反之下滑。陶诗言等对梅雨锋降水的实例分析得出,“锋生过程使梅雨锋上出现强烈的上升运动;强降水出现时,850 hPa水平锋生函数也强”[4]。这与本文的理论结果吻合。
(3) 暖平流时产生上滑,冷平流时产生下滑,此项作用远小于前两项。
2.2 锋面滑升运动与风场的关系对y方向的运动方程取对x的偏导数(忽略f的变化),得
| $ \frac{{\partial u}}{{\partial x}} = \frac{{\partial {u_g}}}{{\partial x}} - \frac{1}{f}\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial v}}{{\partial x}}} \right) $ | (9) |
如图 2,由于y方向与锋面平行,故有

|
图 2 锋面上地转风分布示意图 Fig. 2 Sketch map for the distribution of geostrophic wind on frontal surface |
| $ {\frac{{\partial u}}{{\partial x}} = \frac{1}{{\Delta x}}\left( {{u_{g2}} - {u_{g1}}} \right) - \frac{1}{f}\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial v}}{{\partial x}}} \right)\;\;\Delta x < 0} $ | (10) |
式(10)表明:
(1) 垂直锋面方向的地转风沿锋面向上增大时,暖空气沿锋面上滑,反之下滑。
(2) 锋区中气旋式涡度增大时,暖空气沿锋面上滑,反之下滑。由位涡守恒亦可得到锋面滑升与涡度变化的关系,位涡pv的表达式为[5-6]:
| $ pv = - g\left( {\zeta + f} \right)\frac{{\partial \theta }}{{\partial p}} + g\left( {\frac{{\partial v}}{{\partial p}}\frac{{\partial \theta }}{{\partial x}} - \frac{{\partial u}}{{\partial p}}\frac{{\partial \theta }}{{\partial y}}} \right) $ |
在z坐标下,取x轴的方向与锋面垂直,x的正方向由冷指向暖,风随高度的变化用热成风代替,则锋区中位涡pv的表达式可以写成:
| $ pv = \left[ {\frac{1}{\rho }\left( {\zeta + f} \right) - \frac{g}{{\rho fT}}\frac{{\partial T}}{{\partial x}}{\rm{tg}}\alpha } \right]\frac{{\partial \theta }}{{\partial z}} $ |
(tgα为等θ面坡度,即锋面坡度)
由位涡守恒[5-8]可得,当锋区中气旋性相对涡度增大时,会引起锋面坡度或锋面强度加大,从而形成气块沿锋面向上滑升。
3 锋面滑升与天气形势的关系由上述理论结果,可以推得锋面滑升与天气形势有如下关系。
3.1 锋面滑升与地面形势的关系地面倒槽的偏东风使地面锋面移动较慢,而上层锋面一般为偏西风,锋面移动较快,从而易使锋面坡度增大,由2.1节中的(2)可知,此时易使暖空气上滑。由2.2节中(1)的结论也可以得倒槽冷锋有利于产生上滑。同样道理,地面为鞍场时,也易使暖空气上滑。而地面为平浅西风槽冷锋,地面锋面在偏西风作用下移动较快,锋面坡度不易加大,此时暖空气不易上滑。对锋面气旋来说,气旋的北半部相当于倒槽,南半部相当于西风槽,故气旋北半部锋区降水大于南半部锋区降水。
3.2 锋面滑升与地形的关系由于锋面向冷的一侧倾斜,冷锋在移动中,首先是地面锋的移动受到山脉的阻挡,移速减慢,而上层锋面尚未受到阻碍,移速变化不大,从而导致锋面坡度增大,由2.1节中的(1)可知,此时暖空气上滑。另外,锋区有相当宽度,由于锋区前部首先受山脉阻挡,易导致锋区强度加强,由2.1节中的(2)可知,此时暖空气上滑。由2.2节中(1)的结论,也可得地形阻挡有利产生上滑。所以,地形(山脉)的阻挡有利于暖空气上滑。
3.3 锋面滑升与低值气压系统的关系由2.2节中的(2)可知,当锋面上出现气旋式涡度增大时,暖空气上滑。所以,当锋面上出现锋面切变或锋面气旋生成和发展时,暖空气上滑。也就是说,锋面滑升运动并不直接取决于锋面切变或锋面气旋本身,而是与它们随时间的变化有关。在一条锋面上,哪一部分有切变或气旋的生成和发展,哪里就产生暖空气上滑,形成或加强降水。高空(500 hPa以上)槽前一般为辐散,槽越深时,槽前辐散也就越强,所以高空深槽前一般有较强辐散,从而导致下层降压,有利于锋面切变或气旋发展,产生暖空气上滑。因此,配置高空深槽的锋面易产生强降水。
3.4 锋面滑升与温度平流的关系沿锋面冷平流自下向上加强或暖平流自下向上减弱,有利锋面坡度加大, 则有利暖空气上滑;反之不利暖空气上滑。锋区冷平流或暖平流向前方减弱时,有利锋面强度加强,则有利暖空气上滑,当冷暖平流相向而行时,最有利于锋面强度加强,则最有利于暖空气上滑;反之,锋区冷平流或暖平流向前方减弱时。不利锋面强度加强,则不利于暖空气上滑。
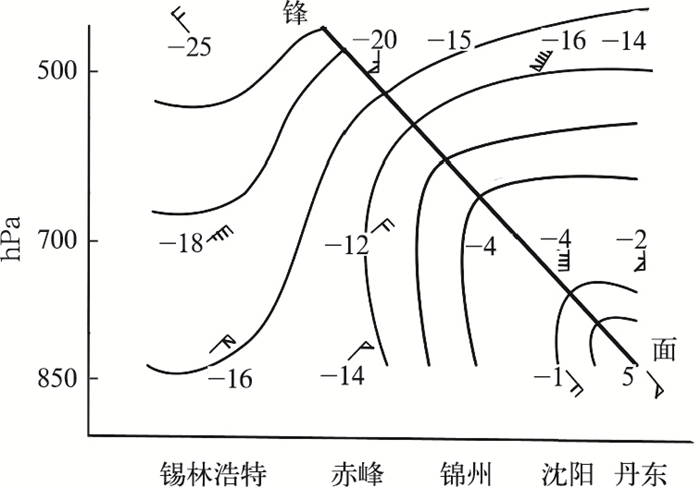
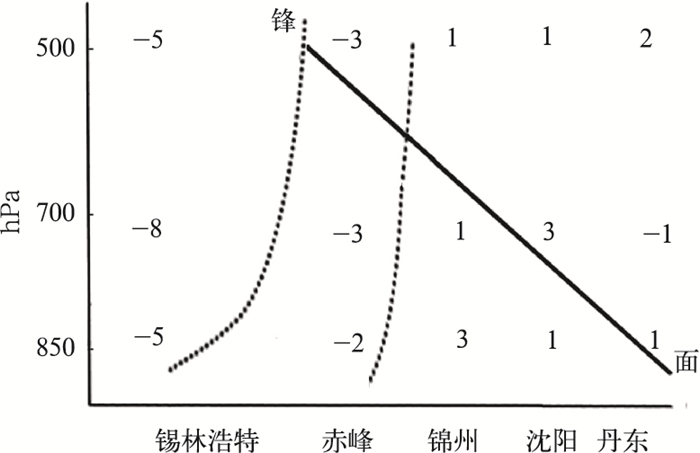
例(1):图 3的变温分布形势,有利暖空气上滑,产生明显降水[9]。例(2):图 4的形势,锋区前界风向随高度升高而顺转,为暖平流;后部风向随高度升高而逆转,为冷平流;特别是850 hPa强SE风(20 m·s-1)迎合西来冷平流,冷暖平流相汇,有利于锋面强度加强。同时,沿锋面自下向上由暖平流转为冷平流(图 5),有利于锋面坡度增大。故该形势非常有利于暖空气上滑,产生明显降水。

|
图 3 2008年1月19日08时Δθse(24小时)空间垂直剖面图(线条为等Δθse线单位:℃) Fig. 3 Vertical cross section of Δθse(24 h) (lines are isopleth of Δθse) at 0800 BT January 19, 2008 |
|
图 4 2007年3月4日08时锋面垂直剖面图 (数字为温度℃细线条为等温线, 粗线为锋面) Fig. 4 Vertical cross section of frontal surface (numerals are temperature in ℃, thin lines are isothermal lines, thick line means frontal surface) at 0800 BT March 4, 2007 |
|
图 5 2007年3月4日08时ΔT(12小时)垂直剖面图(虚线为等ΔT12线, 实线为锋面) Fig. 5 Vertical cross section of ΔT (12 h), (dotted lines are isopleths of ΔT12, thick line means frontal surface), at 0800 BT March 4, 2007 |
(1) 暖空气沿锋面是上滑还是下滑不取决于锋面坡度的大小本身,而取决于其坡度随时间的变化,坡度随时间增大时产生上滑;反之产生下滑。滑升强度与锋面强度(锋区水平温度梯度)成正比。
(2) 暖空气沿锋面是上滑还是下滑不取决于锋面强度的大小本身,而取决于其强度随时间的变化,强度随时间增大时产生上滑;反之产生下滑。滑升强度与锋面坡度成正比。
(3) 暖平流产生上滑;冷平流产生下滑。但由量级分析知,温度平流本身的作用是比较小的,滑升主要取决于温度平流的空间分布(见本文3.4节)。
(4) 锋区中气旋性相对涡度增大时,产生上滑,反之下滑。
(5) 垂直锋面的地转风沿锋面向上增大时,产生上滑,反之下滑。如图 4,沿锋面自下向上由偏东风转为偏西风,有利于产生上滑运动。
致谢:衷心感谢张镡教授悉心指导和石定朴先生热情帮助。
杨大升, 等, 1961. 动力气象学[M]. 北京: 北京大学出版社, 244-252.
|
北京大学地球物理系气象教研室, 1976. 天气分析和预报[M]. 北京: 科学出版社, 104-113.
|
中国人民解放军空军司令部, 1975. 天气学教程[M]. 北京: 中国人民解放军空军司令部出版发行, 134-135.
|
陶诗言, 卫捷, 张小玲, 2008. 2007年梅雨锋降水的大尺度特征分析[J]. 气象, 34(4): 13-15. |
靖春悦, 寿绍文, 贺哲, 等, 2007. 台风海棠造成河南暴雨过程的位涡分析[J]. 气象, 33(4): 60. |
寿绍文, 2010. 位涡理论及其应用[J]. 气象, 36(3): 9-18. DOI:10.7519/j.issn.1000-0526.2010.03.002 |
黄亿, 寿绍文, 傅灵艳, 2009. 对一次台风暴雨的位涡与湿位涡诊断分析[J]. 气象, 35(1): 65-73. DOI:10.7519/j.issn.1000-0526.2009.01.008 |
朱晶, 寿绍文, 何玉科, 2007. 辽东半岛大暴雨的雷达回波及数值模拟分析[J]. 气象, 33(6): 48-49. |
周宁芳, 2008. 全国大部气温明显偏低南方低温雨雪冰冻肆虐[J]. 气象, 34(4): 130-131. |
 2010, Vol. 36
2010, Vol. 36 