引言

定量降水预报在及时、准确的洪水预报和警报中扮演着极其重要的角色。长期的实践表明，准确、及时的流域定量降水预报是延长洪水预报的预见期、提高预报精度、制定正确的防洪调度方案的重要依据，是减免洪水造成损失的重要非工程措施。由于大气降水在时空分布上的变化很大，因此对定量降水预报的可靠性提出了很大的挑战，为了克服单一数值预报模式预报降水的不确定性，近些年来，集合预报技术取得了重大进展^[1], 发展了多模式-多分析集合及其概率预报技术，并且已经应用到多种尺度的数值预报中，使降水的预报技巧有了一定提高^[2-3]，其优势已经得到了国内外众多水文气象学家的肯定^[4-5]，并促使国际上初步形成了一些新的大型水文气象集合概率预报计划^[6]，我国也有部分科研工作者开展了相关的集合预报及其概率预报研究^[7-9]。

多模式-多分析集合预报技术的优点不仅在于能够最大限度的包含定量降水预报的多种可能性，更在于提高对极端天气事件的把握，而这种对所有成员的预报结果的综合应用则可以获得定量降水预报的不确定度，即概率分布。这种无偏的概率分布可以供预报和决策人员参考，提供潜在的决策依据，从而避免极端天气事件发生时可能造成的经济损失和社会危害^[10]。这在单一的模式预报中往往是无法做到的，且与以往仅凭经验或用统计方法做出的概率预报相比，多模式集合预报提供的概率预报产品更具有客观性和定量性，也更具有参考价值^[11]。

在开展集合概率预报研究时，可靠的资料来源是至关重要的。作为WWRP/THORPEX¹子课题的交互式广义全球集合预报(TIGGE: The THORPEX Interactive Grand Global Ensemble)收集了全球10个气象业务中心的全球中期业务集合预报系统的多成员、多要素、多时效(1天至2周)的预报结果，为多模式集合和概率性预报的拓展应用提供了很好的产品支持^[12]。本文利用从世界三大TIGGE资料存储中心之一的中国TIGGE资料数据存储中心获得的ECMWF、NCEP和CMA等三套全球集合预报系统多成员逐日预报降水资料，针对淮河流域上游的大坡岭-王家坝区域，对TIGGE提供的三套集合预报系统降水预报效果做出评估，并探索拓展多模式流域集合概率预报的可行性。

¹http://www.wmo.int/pages/prog/arep/wwrp/new/thorpex_new.html

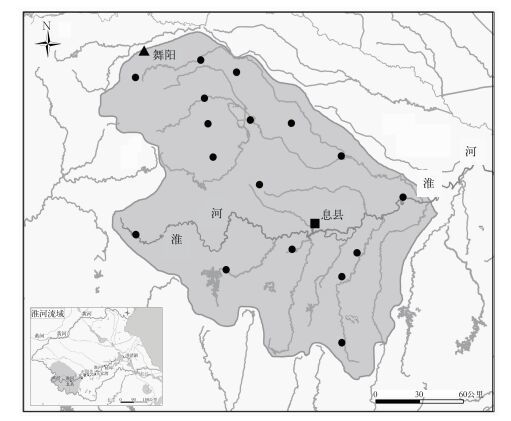
1 研究区域和资料

本文的研究区域为淮河上游的大坡岭-王家坝流域，流域的海拔高度一般在200~500 m之间，面积约30630 km²，作为淮河流域源头的桐柏山区即位于研究流域的西部，研究区域及区域内19个雨量测站的空间分布状况如图 1所示。

实况降水资料为逐日00~00时的24小时累积雨量。TIGGE三套集合预报系统(以下简称EC、NCEP、CMA，下同)的模式降水结果时段为2008年7月1日至8月6日，起报时间为每日00时，输出间隔6小时，各套集合预报系统的集合成员数等有关数据可参见表 1。

根据EC、NCEP和CMA各成员输出的不同时间间隔的降水，首先形成每个成员降水不同预报时效的24小时累积降水，使用双线性插值方法获得流域内站点的降水预报值。由于三套集合预报系统的空间分辨率不同，在构建超级集合平均(简称GrandE，下同)时，首先通过双线性插值方法将CMA的较高分辨率格点数据转化为1°×1°的格点数据，使三集合预报中心的空间分辨率保持一致，然后对三集合预报系统共87个成员采用了等权重平均方法计算得到超级集合平均，在计算超级集合平均时，我们假定各个成员均等效地代表了某种可能性。

由于EC、NCEP和CMA的预报时效不同，本文只对1~10天的预报结果进行分析，为叙述简便，全文用世界时。

2 检验方法 2.1 TS评分

TS评分是我国气象预报业务中常用的基于两分类的评分方法^[13-14]，作为对确定性预报的评分标准，已经纳入了业务预报评价体系^[15]。TS评分的计算公式为：

$TS = {N_A}/({N_A} + {N_B} + {N_C})$

(1)

预报偏差B的计算公式为：

$B = ({N_A} + {N_B})/({N_A} + {N_C})$

(2)

式中N_A、N_B、N_C和N_D分别为降水的报对次数、空报次数和漏报次数，以及预报无降水正确次数。TS值越大表示预报结果越好。B表示预报有降水的次数和观测有降水的次数之比，当B等于1时表示预报是无偏的，大于1时为存在空报，小于1时表示有漏报^[16]，合理的B值一般在1~2之间^[14]。

2.2 Brier(BS)评分

Brier评分定义了一种均方概率误差，该方法综合考虑了可靠性、分辨能力和不确定性。Brier评分已在定量降水概率预报评估中得到了广泛应用^[17]。其具体计算公式为：

$BS = \frac{1}{N}\sum\limits_{i = 1}^N {{{({f_i} - {o_i})}^2}} $

(3)

式中N为两分类事件的预报数，f_i表示某一天气事件发生的预报概率，o_i表示实况，事件发生o_i为1.0，事件不发生o_i为0.0。BS的值在0和1之间，BS值越小越好，BS为1表示评分最差，预报失效。

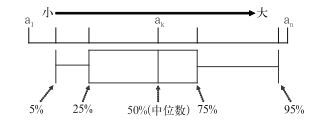
2.3 百分位数

百分位数属于分位数的一种²，是指将一组n个数据按从小到大的顺序排列，并计算相应的累计百分位，则某一百分位所对应数据的值就称为这一百分位的百分位数，第50百分位为中位数，图 2给出了一个百分位图的示例及常用的百分位点。百分位数提供了有关各数据项如何在最小值和最大值之间分布的信息，是用于衡量数据位置的量度，一般使用方框-盒须图来表现百分位数的分析结果^{[3, 18]}，方框-盒须图的拉伸度越小表示包含的可能性越少，预报结果相对集中；反之，拉伸度越大表明包含的可能性越多，预报结果比较分散。陈辉等^[19]在我国的高温中暑等级确定中使用了该方法，由于百分位数计算有多种不同的方法^[20-21]，本文中使用的是由Hyndman^[20]提出的一种经验方法，具体公式为：

${Q_i}\left( p \right) = \left( {1 - \gamma } \right){A_{(j)}} + \gamma {A_{(j + 1)}}$

(4)

²Lane, David.“Percentiles.” Connexions.April 20, 2008.http://cnx.org/content/m10805/latest/

式中j=int(p×n+(1+p)/3)，γ=p×n+(1+p)/3-j，其中Q_i(p)为第i个百分位降水，A为升序排列后的多个成员的预报降水值，p为分位数，本文中取第5、25、50、75和99百分位，n为序列总数，即表 1所示三套集合预报系统的成员数，j为第j个序列的值。

3 结果分析

在对降水进行TS和Brier评分时，根据国家气象中心业务常用的降水量级划分标准将降水划分为四个等级，即晴雨、小雨、中雨和大雨，考虑模式的降水预报值和模式误差，选择1.0 mm作为模拟晴雨降水的阈值上限，由于模式通常对大雨以上量级降水的模拟能力较差，且实际观测中大雨以上量级的降水出现的频次较少，在TS和Brier评分中未对大雨以上量级的降水进行评估，而在百分位降水评估分析中考虑了所有量级的降水。

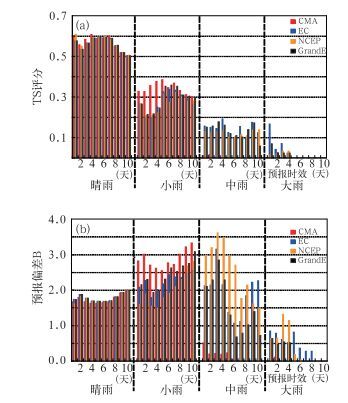
3.1 TS评分和预报偏差B分析

图 3所示为三套集合预报系统及其超级集合的集合平均对四个等级降水不同预报时效的TS评分和预报偏差B比较。在计算集合平均时，EC、NCEP和CMA使用的成员数见表 1，超级集合则为三套集合预报系统共87个成员的平均。

对于晴雨TS评分(图 3a)，CMA、NCEP、EC及其超级集合在该研究区域有类似表现，TS评分均在0.5~0.6之间。小雨的TS评分表明(图 3a)：1~5天的预报中，CMA表现最佳，评分在0.3以上，而EC和NCEP的评分一般为0.2左右，同CMA相比稍差，超级集合预报的结果同EC和NCEP的结果相当；5~10天的预报中，三套集合预报系统及其超级集合的TS评分均在0.3左右。尽管CMA对1到5天的预报有最佳表现，但其小雨的预报偏差B在2.5以上(图 3b)，可见CMA在对小雨预报准确的同时，也有很高的空报率。与此同时，中雨和大雨的TS评分和预报偏差B也表明，CMA对小雨提前1~5天预报准确率的提高是以对整体降水量预报偏低为代价换来的，即CMA预报的降水普遍偏小，从而导致了对小雨较好的预报能力和对中雨及以上量级的降水预报不足。随着预报时间的延长，EC和NCEP的中雨TS评分均逐渐从1天的0.15减至10天的0.10(图 3a)，同时预报偏差B显示，对中雨1~10天的预报中，NCEP均有较高的空报率(图 3b)。对大雨而言，EC和NCEP 1~4天的预报有较低的预报准确率，4天之后的降水基本失去了预报能力，尽管大雨预报的偏差B显示EC对8天后的降水也有一定的预报能力。

与EC、NCEP和CMA三套独立的集合预报系统相比，超级集合对四个量级降水的预报能力稍优于或等同于EC。分析其原因，在进行集合平均计算时，三套集合预报系统使用的是各自多个成员的平均，但超级集合是87个成员的平均，从而会造成超级集合的结果倾向于成员数多的集合预报系统的结果。为了从更多的角度对降水进行评估，同时对超级集合的结果进行检验，下面从概率预报的角度对预报结果进行评估。

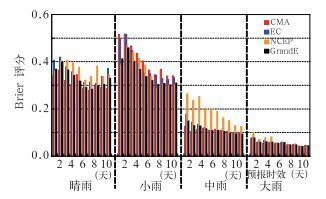
3.2 概率预报 3.2.1 Brier评估分析

进行Brier评分时，CMA、NCEP和EC集合预报系统的成员数等信息见表 1。图 4为三集合预报系统及其超级集合对四个降水等级不同预报时效的Brier评估分析。

四个降水等级的Brier评分表明(图 4)，整体而言CMA的晴雨Brier评分最优，BS值从1天的0.34逐渐减至10天的0.28，而超级集合的Brier评分逐渐从1天的0.37减至10天的0.33，同CMA相比稍差，但优于EC和NCEP集合预报系统的表现。对于Brier评分随着预报时间的延长逐渐减小的变化趋势，Pappenberger等^[4]在对EC降水预报进行概率分析时也遇到了相同的问题，据文献[22]分析，可能是随着预报时效的延长，模式误差增大，预报降水逐渐减弱造成的，有待于进一步研究。对小雨，随着预报时效从1天延长至10天，三套集合预报系统及其超级集合的Brier评分均逐步降低，超级集合给出了近似最优的结果，CMA表现最差，这与3.1节分析的结果相符。中雨和大雨的Brier评分显示，超级集合具有最优或次优的预报结果，其次是EC，但CMA对这两个量级的降水仍有一定的预报能力，表明个别成员具有预报中雨和大雨的能力。中雨的Brier评分中，NCEP最差，这与TS评分中NCEP有较高的预报偏差相一致。中雨和大雨的Brier评分同时也表明，各集合预报系统对中雨和大雨均有一定的预报能力，即某些成员成功捕捉到了这种可能性，而集合平均往往会由于平滑作用而导致对这些量级降水的预报能力不足。

3.2.2 百分位降水分析

TS评分和Brier评分都是根据一定的样本量进行计算的，在计算过程中没有考虑流域内降水的时间和空间变化，下面通过百分位数方法以更直观的方式对三套集合预报系统及其超级集合的降水预报结果进行分析。

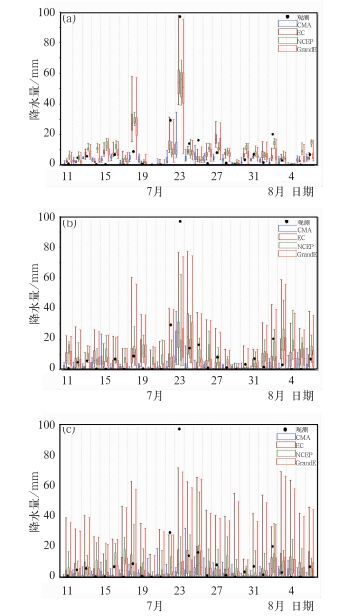
首先分析流域面雨量预报效果。图 5为2008年7月11日至8月6日CMA、NCEP、EC及超级集合在大坡岭-王家坝流域不同预报时效的面雨量预报结果的百分位评估。1天、5天和10天的预报中，三套集合预报及超级集合均较好地预报了降水的变化趋势，随着预报时效的延长，方框—盒须图的拉伸度逐渐变大，并呈现朝降水量级小的方向移动的趋势。1天预报时，方框-盒须分布紧凑，除个别日期外，观测降水均落在第5和99百分位内，离散度较小，多个成员的预报降水比较接近，同观测相比偏差较小。超级集合预报则综合了多个集合预报系统的可能性，预报效果优于单个集合预报系统，如7月13日、16日、18日、22日和23日的一天预报，CMA和NCEP均未能很好地预报出这种可能性，超级集合的结果则体现出这种可能性(图 5a)。与1天的预报结果相比，5天和10天预报时三套集合预报系统及其超级集合的方框-盒须拉伸度均显著增大(图 5b和图 5c)，除7月23日外，观测降水均落在超级集合的第5和99百分位内，超级集合的表现同EC相当，优于NCEP和CMA的表现。对于10天的预报，即使是第50百分位降水，多日预报的第50百分位降水为0.0mm，即至少有50%的成员预报的降水为0.0mm，同1天和5天的预报相比有较大误差。

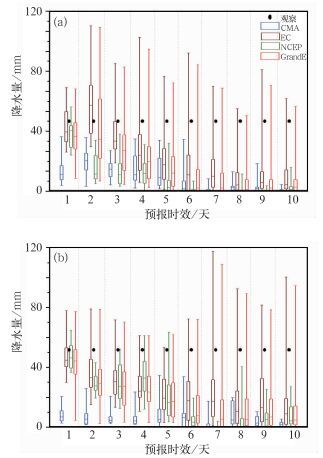
其次，分析流域单站雨量的预报效果。7月23日的强降水代表了某种极端事件的发生，1天的预报中很好地捕捉了这一强降水可能性，但5天和10天的预报中，对该强降水的预报能力均显得不足。图 6给出了观测到中等量级降水的舞阳和息县站1~10天降水的预报评估，两站在流域内的位置可参见图 1所示。舞阳和息县的24小时观测降水分别为70.1 mm和51.6 mm，均达到了暴雨量级。随着预报时效从1天延长至10天，除CMA外，方框—盒须图的拉伸度逐渐增大，方框所表示的第25、50和75百分位降水呈减小的趋势，第99百分位降水同观测的偏差逐渐增大。根据CMA预报得到的两站点不同降水预报时效均有严重的低估，息县站尤为显著，即使是第99百分位降水同观测相比仍然有10.0 mm以上的偏差。EC对两站1~5天的预报把握较好，对6天之后的预报基本保持稳定状态，第75百分位降水低于观测，但EC个别成员仍然很好地预报了该天的降水量。NCEP在息县站1~5天的预报均较好，但在舞阳站仅保持了1天，1天之后的预报均有严重低估，且NCEP所有成员都没能很好的预报出降水量。超级集合的预报结果同EC的相当，但随着预报时效的延长，超级集合方框-盒须图的拉伸度要小于EC，说明各成员降水预报的可能性更为集中，这在图 5b和5c中也有体现。但需要注意的是，对于6~10天的预报，三套集合预报及其超级集合第50百分位降水值均为0.0 mm，也就是说至少50%的成员预报无降水，结合图 5的分析结果，说明在直接使用集合降水预报时，对于超过5天的预报，即使是超级集合预报结果也要谨慎。

为了更直观地对三套集合预报及其超级集合预报的降水效果进行比较，图 7给出了2008年7月22日00时至23日00时CMA、NCEP、EC及其超级集合第95百分位降水的空间分布同观测降水的对比。图中数字为雨量值，为使降水的空间分布更为明显，用圆点表示雨量的相对大小。观测降水显示，流域内的降水整体呈北高南低的分布，最大降水中心在流域的东北部，站点观测雨量达到了198.0 mm，为大暴雨，最小值在流域中东部，为46.2 mm，流域内19个观测站的平均雨量值为97.0 mm，为暴雨级别(图 7a)。三套集合预报及其超级集合预报降水的空间分布表明，强降水中心均在流域北部，随着纬度的减小向南逐渐减弱。比较图 7(b)~7(e)发现，各集合预报在量级上有很大差别：CMA预报效果较差，站点最大值为53.0 mm，位于流域西北部，19个站点95百分位降水范围在10.7~53.0 mm，均值仅为30.2 mm(图 7b)；其次为NCEP，第95百分位降水在46.6~85.1 mm之间，最大雨量为85.1 mm，位于北部稍偏南位置，就最大雨量点出现的位置而言同实况观测最为接近，但预报降水值偏小(图 7c)；EC的预报结果是三个集合预报系统中最优的，19个站的第95百分位降水值在44.5~114.6 mm，其中5个站超过100.0 mm，但预报降水最大的站点位于流域西部，同实况最大值相比空间偏差较大(图 7d)；超级集合的降水由于综合了87个成员的降水结果，第95百分位降水在44.6~98.1 mm之间，就最大站点降水的位置而言与NCEP一致，预报降水值为98.1 mm，19站的平均雨量值为74.0 mm，同EC的85.4 mm相比稍差，但优于NCEP的70.5 mm和CMA的结果(图 7e)。

通过以上分析，就降水量级而言EC的结果同观测最为接近，NCEP对超级集合预报强降水的位置贡献最大，而EC对降水值的贡献最大。随着预报时效的延长，多模式集合对降水的空间分布仍有一定的预报能力，但三套集合预报系统的预报降水值均显著减弱。

4 结论和讨论

使用TIGGE中国中心提供的2008年7月1日至8月6日CMA、NCEP和EC三套集合预报1~10天的降水预报，结合本文研究区淮河上游的大坡岭-王家坝流域内19个观测站的24小时逐日降水，利用TS、Brier和百分位评分方法，对三套集合预报及其超级集合的降水预报结果进行了确定性的和概率性的评估，得到的主要结论如下：

(1) 超级集合的TS评分优于或等同于EC，其次是NCEP，CMA对晴雨预报较好，小雨1~5天预报时的TS评分甚至超过了超级集合和EC，但存在较大的空报率，且对中雨及以上量级降水缺乏预报能力；

(2) Brier评分结果表明，1~10天的降水预报中，三套集合预报系统及其超级集合对四个等级的降水均有一定的预报能力，即都有部分成员捕捉到了这种可能性，但集合平均(确定性预报)通过平滑作用削弱了这种可能性，从而使得对较大量级和较长预报时间的降水预报能力不足，但超级集合的Brier评分总体上要优于单个集合预报系统；

(3) 流域面雨量的百分位降水分析表明，预报时间越短，多成员预报降水越接近观测降水，随着预报时间的延长，中雨以下量级降水出现的比率逐渐增加，方框-盒须图的拉伸度逐渐增大，并朝着降水量级减小的方向移动，即对中雨及以上量级降水的预报能力逐渐减弱。尽管CMA预报的降水量级往往偏小，但对于超级集合而言，仍然代表了弱降水出现的可能性；

(4) 站点降水的时间变化个例分析表明，1~5天的预报中，EC和超级集合均对降水做出了很好的预报，实际观测降水居于多种可能性的适中位置，但对于5~10天的预报，多数成员预报的降水偏小。超级集合由于考虑了更多的降水可能性，19个观测站第95百分位降水的量级和空间分布同观测更为接近。

(5) TS评分、Brier评分和百分位降水是从不同的角度对预报结果进行分析。TS评分一般适用于两分类预报结果的评估，即从某一天气现象出现与否的角度对预报结果进行评价。Brier评分适用于多模式或多成员预报结果，是从概率的角度分析有多少集合成员捕捉到了某一天气现象，用0.0~1.0之间的一个数字提供该类天气现象发生的可能性，缺点是不能给出具体的量值^[23]；百分位降水评分则根据多个成员的预报结果直接给出降水的分布状况，并显示整体成员预报降水的变化趋势和预报极端降水状况。正是由于百分位预报提供的极端事件的概率信息，当前的流域水文气象预报中已经使用了这一方法^[24-25]。

(6) 随着集合预报系统和概率预报方法的发展，以及对极端天气事件科学认识的深入，基于当前的数值预报结果提供3~10天的流域洪水概率预报，西方发达国家已经开始了这方面的尝试，并初步证实了这一技术的可行性和巨大发展空间^[26-27]，针对我国暴雨洪涝多发的流域开展相关研究势在必行。

要强调的是，本文针对三个集合预报系统一个多月预报结果的评估结果说明三个中心集合预报系统对降水均具有一定的预报能力，其中EC的预报是较好的^[12]。需要指出的是，本研究在从模式预报获得站点降水预报时，使用了双线性插值方法，插值时没有考虑地形地势等因素的影响，在进行降水评估时也没有考虑这方面的影响。另外，部分学者对单集合预报系统所需成员数的多少进行过研究^{[25, 28]}，但在进行多模式超级集合时，如何设定各不同集合预报成员的权重，以及使用多少成员合适，当前仍没有统一的认识^[29]，从表 1可得知本研究使用的三个中心集合成员数不同；EC的集合成员数为51，多于NCEP的21个成员和CMA的15个成员数之和。此外，本研究在求取集合平均时没有区分个体成员的权重，使用了等权重方法，等等。对于这些问题值得在今后的研究中进行深入探讨。